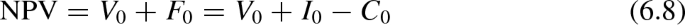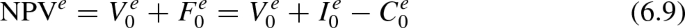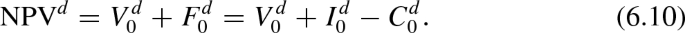Abstract
We show how to evaluate a project in terms of cash flows (based on NPV), incomes (based on residual income, RI), and capitals (based on value added or net future value, NFV), taking into account various perspectives: investment vs. financing, levered vs. unlevered, financial structure vs. capital structure, standard discounting vs. modified discounting, actual cash flows vs. potential dividends. We present 12 discountedcash- flow methods.
The fundamental economic and financial decision of the firm is that of determining the level and composition of its investment. Firms can invest in either physical assets or financial assets (securities). Such investment decisions determine the firm’s future income \(\ldots \) A firm must make two additional and related financial decisions: first, how much of its current income to pay out to the owners of the firm (the dividend decision), and second, the amount and type of financial securities to issue (the financial structure decision). These constitute the financing decisions of the firm. Therefore, firms are considered to make two general types of financial decisions: investment decisions and financing decisions.
Haley and Schall (1979, p. 3)
We agree that managers with reliable intuition (that is, a discriminating gut) and the experience to make sound judgements will − and should − ultimately make the major corporate investment choices.
However, analytical tools ...can help see through the complexity ...inherent in the evaluation of a major investment. It is our belief that, by using these tools and taking a more disciplined approach to valuation, managers’ judgment will be enhanced and they will make better investment choices.
Titman and Martin (2011, p. 3)
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The associated benchmark systems are then described by the respective transposed Matrices \((\varvec{V}^e, \varvec{I}^{Ve}, \varvec{F}^{Ve})\) and \((\varvec{V}^d, \varvec{I}^{Vd}, \varvec{F}^{Vd})\).
- 2.
If \(V^e_{t-1}<0\), the rate \(r_t^e\) acts as a MAFR for shareholders; if \(V^d_{t-1}<0\) (admittedly, a rather-peculiar-but-not-impossible case), \(r_t^d\) acts as a MAFR for debtholders; if \(V_{t-1}<0\), \(r_t\) acts as a MAFR for capital “borrowers” (equityholders \(+\) debtholders).
- 3.
More generally, one gets
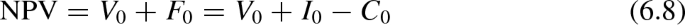
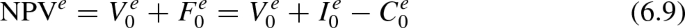
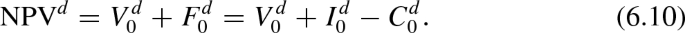
If \(I_0=I^e_0=I^d_0=0\), then \(F_0=-C_0\), \(F^e_0=-C^e_0\), and \(F^d_0=-C^d_0\).
- 4.
Symmetrically, the firm makes a value-neutral financing.
- 5.
The sign and magnitude of the debt NPV depends on the ability of the company of borrowing at a higher or lower cost than the cost of financing in a normal market as opposed to the ability of debtholders to lend money at an above-normal interest rate (this also depends on several types of imperfections that may arise in the market). A positive project NPV associated with a negative equity NPV may also reveal a debt overhang problem, which results in under-investment (see Berk and DeMarzo 2014, pp. 554–555; Myers 1977). Evidently, if the firm borrows from a lender at a rate \(i^d\) such that \(r^d<i^d\) (implying \(C^d_t<V^d_t\)), then the firm’s managers should preferably borrow from the market, not from that lender; however, as long as the equity NPV is positive, the undertaking of a project with positive debt NPV increases equityholders’ wealth. Vice versa, if the firm’s managers happen to find a lender available to lend money at \(i^d<r^d\), then the firm is able to create value out of that borrowing. The ROD may also differ from \(r^d_t\) (implying nonzero debt NPV) whenever the analysis of the project is made not when the firm raises the debt capital but, rather, at a later stage. In that case, the firm may be using debt on which it pays an interest rate \(i^d_t\) different from \(r^d_t\).
- 6.
For \(t=0\), the benchmark Matrix as such is not valid. For it to be valid, one should define \(r_0V_{-1}\) as being equal to \(F_0+V_0\).
- 7.
If no shares are issued at time 0 (e.g., debt financing or internal financing is used), the ROE in the first period is not defined, so that (6.23) may not be written as such. It may be written as
$$(C^e_0+I_1)(1+i^e_2)(1+i^e_3) \cdot \ldots \cdot (1+i^e_n)= \sum _{t=1}^n F^e_t (1+i^e_{t+1})(1+i^e_{t+2}) \cdot \ldots \cdot (1+i^e_n).$$ - 8.
See also Sect. 1.3.
- 9.
- 10.
Strictly speaking, we must assume that either the bank’s investment of \(\$\)60 is equity financed or that it is financed with debt and the debt is value-neutral; otherwise, \(\$\)0.938 measures the bank’s NPV but not the bank’s equity NPV.
- 11.
Assuming the debt rate, \(i^d\), is constant, then \(i^d=10.78\%\), for \(65=35/1.1078+41/1.1078^2\).
- 12.
Assuming the equity COC is constant, this implies \(r^e=25\%\). To see it, consider that \(V_0=\text {NPV}+C_0=-5.8+150=144.2\) and \(V^d_0=\text {NPV}^d+C_0=-7.36+65=57.64\) whence \(V^e_0=144.2-57.64=86.56\). Also, \(F^e_1=120-35=85\) and \(F^e_2=70-41=29\). Hence, \(86.56=85/1.25+29/1.25^2\).
- 13.
The reason why Jerry lends money to Tom at conditions which are better (for Tom) than the security market may have to do with some kind of market imperfections or with bounded rationality or with other side effects on the part of Jerry’s economic activities. Whatever the reasons, these situations do occur in real life.
- 14.
The optimal financing policy for the bank would be to set the account rate as small as possible, so as to snap additional value from the customer (obviously, this conflicts with the optimal investment policy of the customer, who aims at maximizing the return on the capital invested. If the account rate is 5%, the value is neither created nor destroyed for both the bank and the customer).
- 15.
The associated benchmark systems are then described by the respective transposed Matrices \((\varvec{V}^o, \varvec{I}^{Vo}, \varvec{F}^{Vo})\) and \((\varvec{V}^l, \varvec{I}^{Vl}, \varvec{F}^{Vl})\).
- 16.
The value of a firm’s operating assets is also known as the enterprise value (see Berk and DeMarzo 2014, p. 28). In terms of the project, \(V^o_t\) is the increase of the enterprise value caused by the project undertaking.
- 17.
In principle, one might define a mirror equation of (6.21):
$$\begin{aligned} i^l_t&=i_t+\frac{C^o_{t-1}}{C^l_{t-1}}(i_t-i_t^o)\nonumber \\ r^l_t&=r_t+\frac{V^o_{t-1}}{V^l_{t-1}}(r_t-r_t^o).\nonumber \end{aligned}$$Again, we stress that the two rates refer to project system and benchmark system, respectively. That is, they refer to two alternative courses of action, the factual one (undertaking the project) and the counterfactual one (replicating the project by investing in the market). In the first formula, pro forma book values are considered; in the latter formula, market values are taken into account.
- 18.
The net-debt COC is known whenever both the debt COC, \(r^d_t\), and the non-operating COC, \(r^l_t\), are known or, alternatively, whenever the debt COC is known and the financial assets have the same risk as the debt, which implies that the non-operating COC is equal to the debt COC.
- 19.
The negative value of non-operating assets signals that, undertaking this project, the firm absorbs additional resources from non-operating assets. In particular, consider that, at time 1, the CFL is negative and equal to \(F^l_1=-23{,}537\). If one replicates the CFL vector in the market, one receives, at time 1, an asset which is worth \(V^l_1=21{,}278\) (see Table 6.7) but will have to disburse \(|F^l_1|=23{,}537\); the difference is \(-2{,}259=21{,}278-23{,}537=V^e_1+F^l_1\). Discounting back by one period at 3% one gets \(V^l_0=-2{,}259/1.03=-2{,}193.\) Therefore, to invest in the replicating portfolio boils down to taking on a short position. The (negative) price of the replicating portfolio is the market value of the non-operating assets.
- 20.
In the 80% case, the vector of asset ROIs was \(\varvec{i}=(6.68\%,\, 8.51\%,\, 10.97\%,\, 14.38\%,\, 19.4\%)\).
- 21.
The increase in CFO is just equal to the product of the tax rate and the interest income generated by the 80% payout, \(\tau I^l_t\). Precisely, the change in the CFO stream is (0, 0, 155, 318, 489, 667).
- 22.
In the 80% case, the CFAs are smaller than the respective CFOs because some cash is retained.
- 23.
This assumption means that the return on net debt is equal to the required return on net debt. It may occur for various reasons, including (but not limited to) the case where both the debt and the liquid assets are value-neutral operations (i.e. \(i^d_t=r^d_t\) and \(i^l_t=r^l_t\) for every t).
- 24.
The operating after-tax WACC is, by far and large, the most widely known COC in finance, which explains the reasons why it is often called “WACC” with no other specifications.
- 25.
What is, in general, the proper discount rate for tax shield, \(r^{\text {TS}}\)? The problem of finding the correct discount rate has been investigated extensively in the literature but, to date, no agreed upon solution have been advanced. The determination of \(r^{\text {TS}}\) is a subtle issue because it depends on the risk of \(\tau I^{\mathcal D}_t\), which in turn depends on the set of assumptions made. In particular, if the risk of the tax shield is equal to the risk of debt, then \(r^{\text {TS}}_t=r^{\mathcal D}_t\); if the risk of the tax shield is equal to the risk of the unlevered operating assets, then \(r^{\text {TS}}_t=k^{uo}_t\). Other assumptions are possible and the determination of \(r^{\text {TS}}_t\) will depend on the financing policy and on the level of the prospective operating income as opposed to net interest (if the latter is greater than the former, no tax saving arises) (see Myers 1974; Miles and Ezzell 1980, 1985; Inselbag and Kaufold 1997; Harris and Pringle 1985; Lewellen and Emery 1986; Taggart 1991; Fernández 2002, 2004; Arzac and Glosten 2005; Cooper and Nyborg 2006, 2007, 2008; Grinblatt and Liu 2008; Massari et al. 2008; Dempsey 2013).
- 26.
Equation (6.80) is equal to Eq. (7) in Dempsey (2013). See also Cooper and Nyborg (2006).
- 27.
In particular, the authors assumed a riskless debt: \(r^{\mathcal D}=r_f\).
- 28.
The variations of the WACCs are very small, owing to the simple structure of this operation. In particular, (6.73) may be reframed in such a way that the pre-tax WACC is computed as a weighted mean of \(k^{uo}\) and \(r^{\text {TS}}\), where the weights are \(V^{uo}_{t-1}/V^o_{t-1}\) and \(V^{\text {TS}}_{t-1}/V^o_{t-1}\):
$$ r^o_t=\frac{k^{uo}_t V^{uo}_{t-1}+ r^{\text {TS}}_t V^{\text {TS}}_{t-1}}{V^{uo}_{t-1}+V^{\text {TS}}_{t-1}} =\frac{0.1 V^{uo}_{t-1}+ 0.03 V^{\text {TS}}_{t-1}}{V^{o}_{t-1}}. $$It may be checked that the weight \(V^{uo}_{t-1}/V^o_{t-1}\) gradually increases as t increases, from 94.49% to 95.71%, which gradually pushes the pre-tax WACC toward \(k^{uo}=10\%\) (at a pace of about 0.01% a year).
- 29.
See Table 6.31 for other relations involving the unlevered cost of assets.
- 30.
Analogous relations may be set up for modified CFEs so that they are discounted at \(r_t\) or at \(r^{u}_t\):
$$\begin{aligned} \begin{aligned} V^e_{t-1}&=\frac{V^e_t+F^e_t-(r_t-r^d_t)\cdot V^d_{t-1}}{1+r_t}\\ V^e_{t-1}&= \frac{V^e_t+F^e_t-\bigl (r^{u}_t-r^d_t(1-\tau )\bigr ) \cdot V^d_{t-1}}{1+r^{u}_t}. \end{aligned} \end{aligned}$$(6.98).
- 31.
We remind the reader that \(r^{\text {TS}}\) is the discount rate for \(\tau I^{\mathcal D}_t=\tau (I^d_t-I^l_t)\), whereas \(r^{\text {GTS}}\) is the discount rate for \(\tau I^d_t\). The first one follows a capital structure perspective (net tax savings), the second one follows a financial structure perspective (gross tax savings).
- 32.
See also Remark 4.6.
- 33.
In this case, the interest rate on debt is smaller than the interest rate on liquid assets: \(0.15=i^l>i^d=0.08\). However, for a capital asset investment, it might be unrealistic (albeit not impossible) to borrow funds at a given interest rate \(i^d\) and invest them in financial assets \(i^l\) with a higher expected return (i.e., the condition \(i^l>i^d\) is usually not fulfilled).
- 34.
If this assumption is made, one may not make the additional usual assumption \(i^d=r^d=0.08\), because this would imply \(r^d>r^e\) which is not legitimate (see Remark 6.1).
- 35.
Admittedly, if one assumes, as usual in capital budgeting, that \(\text {TP}_t=0\) for every \(t\in \mathbb {N}^0_n\), this problem does not arise.
- 36.
Block (2011) surveyed 255 top-ranking financial officers. Only 20.3% of them use debt rebalancing.
- 37.
The relationships between the conventional CCF method and the textbook WACC method has been investigated in many academic contributions, especially in relation to firm valuation (e.g., see Arditti and Levy 1977; Ben-Horin 1979; Chambers et al. 1982; Ruback 2002; Fernández 2002; Tham and Vélez-Pareja 2004; Booth 2007; Cooper and Nyborg 2007; Jagannathan et al. 2017).
- 38.
In Example 5.8, the \(\$\)12 is just the project’s normal profit under this perspective (and \(\$3\) is the residual income).
- 39.
The equality \(F_t^*=C_{t-1}(1+r_t)-C_t\) logically derives from the assumption that the benchmark asset replicates the project’s capital amounts: \(C_t=C^*_t\). One may also write \(F_t^{*}=I^{*}_t-(C_t-C_{t-1})=[\text {using}\,(6.123)]=I_t^{*}-(I_t-F_t)\).
- 40.
In principle, other RIs may be built. We will not pursue all the possibilities for constructing RIs and will confine ourselves to (a subset of) the above mentioned RIs.
- 41.
The reader should not confuse \(V^{uo}_0(\text {RI})\) with \(V^{uo}_0\):
$$\begin{aligned} V^{uo}_0&=\sum _{t=1}^n F^{uo}_t [(1+k^{uo}_1)(1+k^{uo}_2)\cdot \ldots \cdot (1+k^{uo}_t)]^{-1}\\ V^{uo}_0(\text {RI})&= \sum _{t=0}^n \text {RI}^{uo}_t [(1+r^{uo}_1)(1+r^{uo}_2)\cdot \ldots \cdot (1+r^{uo}_t)]^{-1} \end{aligned}$$The former is the discounted sum of FCFs, supplying the project’s unlevered operating value; the latter is the discounted sum of \(\text {RI}^{uo}\)’s, supplying the project’s levered operating NPV. Analogously, adopting an asset perspective, no confusion should be made between \(V^u_0\) and \(V^u_0(\text {RI})\):
$$\begin{aligned} V^u_0&=\sum _{t=1}^n F^{u}_t [(1+k^u_1)(1+k^u_2)\cdot \ldots \cdot (1+k^u_t)]^{-1}\\ V^u_0(\text {RI})&= \sum _{t=0}^n {\text {RI}^{u}_{t}} [(1+{r^{u}_{1}})(1+{r^{u}_{2}})\cdot \ldots \cdot (1+{r^{u}_{t}})]^{-1}. \end{aligned}$$ - 42.
- 43.
Adapted from Magni CA (2009c), Splitting up value: A critical review of residual income theories, European Journal of Operational Research, 198(1) (October), 1–22, (p. 5).
- 44.
All numbers are rounded for notational convenience, as always.
- 45.
We remind that a given metric/criterion is NPV-consistent if and only if the decision recommended by that metric/criterion is the same as the decision recommended by the NPV (see also Definition 8.6).
- 46.
Numbers are rounded, as usual.
- 47.
We have assumed \(i^d=r^d=0.03\) so \(\text {NPV}^d=0\) and the project NPV coincides with shareholder value created (see also Table 6.10).
- 48.
The NPV of the agent investing in the benchmark portfolio is obviously zero, as the benchmark portfolio is an equilibrium asset.
- 49.
The RI vector is
$$\mathbf{RI} =(0, -11{,}489, \; -1{,}494,\; 8{,}608,\; 18{,}785,\; 28{,}915)$$whence, discounting with \(\varvec{r}=(8.97\%, 9.28\%, 9.75\%, 10.56\%, 12.39\%)\), one gets \(V_0 (\text {RI})=25{,}592\).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Magni, C.A. (2020). Project Appraisal. In: Investment Decisions and the Logic of Valuation. Springer, Cham. https://doi.org/10.1007/978-3-030-27662-1_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-27662-1_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26775-9
Online ISBN: 978-3-030-27662-1
eBook Packages: Economics and FinanceEconomics and Finance (R0)