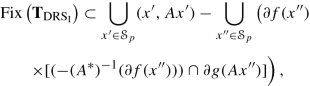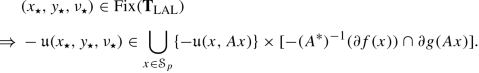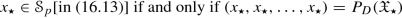Abstract
The breakthrough ideas in the modern proximal splitting methodologies allow us to express the set of all minimizers of a superposition of multiple nonsmooth convex functions as the fixed point set of computable nonexpansive operators. In this paper, we present practical algorithmic strategies for the hierarchical convex optimization problems which require further strategic selection of a most desirable vector from the solution set of the standard convex optimization. The proposed algorithms are established by applying the hybrid steepest descent method to special nonexpansive operators designed through the art of proximal splitting. We also present applications of the proposed strategies to certain unexplored hierarchical enhancements of the support vector machine and the Lasso estimator.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
To the best of the authors’ knowledge, little has been reported on the hierarchical nonconvex optimization. We remark that the MV-PURE (minimum-variance pseudo-unbiased reduced-rank estimator) (see, e.g., [112, 113, 144]), for the unknown vector possibly subjected to linear constraints, is defined by a closed form solution of a certain hierarchical nonconvex optimization problem which characterizes a natural reduced rank extension of the Gauss-Markov (BLUE) estimator [85, 93] to the case of reduced-rank estimator. It was shown in [113] that specializations of the MV-PURE include Marquardt’s reduced rank estimator [97], Chipman-Rao estimator [29], and Chipman’s reduced rank estimator [28]. In Section 16.5.2 of this paper, we newly present a special instance of a hierarchical nonconvex optimization problem which can be solved through multiple hierarchical convex optimization subproblems.
- 3.
The behavior of \((x_{\varepsilon })_{\varepsilon \in (0,1)} \subset \mathcal {X}\) can be analyzed in the context of approximating curve for monotone inclusion problem. For recent results combined with Yosida regularization, see [37].
- 4.
- 5.
By extending the idea in [75], another algorithm, which we refer to as the generalized Haugazeau’s algorithm, was developed for minimizing a strictly convex function in \(\varGamma _{0}(\mathcal {H})\) over the fixed point set of a certain quasi-nonexpansive operator [33]. In particular, this algorithm was specialized in a clear way for finding the nearest fixed point of a certain quasi-nonexpansive operator [8] and applied successfully to an image recovery problem [39]. If we focus on the case of a nonstrictly convex function, the generalized Haugazeau’s algorithm is not applicable, while some convergence theorems of the hybrid steepest descent method suggest its sound applicability provided that the gradient of the function is Lipschitzian.
- 6.
Often \(\langle \cdot , \cdot \rangle _{\mathcal {X}}\) denotes 〈⋅, ⋅〉 to explicitly describe its domain.
- 7.
(Strong and weak convergences) A sequence \((x_n)_{n \in \mathbb {N}} \subset \mathcal {X}\) is said to converge strongly to a point \(x \in \mathcal {X}\) if the real number sequence \((\|x_n - x\|)_{n \in \mathbb {N}}\) converges to 0, and to converge weakly to \(x \in \mathcal {X}\) if for every \(y \in \mathcal {X}\) the real number sequence \((\langle x_n - x, y \rangle )_{n \in \mathbb {N}}\) converges to 0. If \((x_n)_{n \in \mathbb {N}}\) converges strongly to x, then \((x_n)_{n \in \mathbb {N}}\) converges weakly to x. The converse is true if \(\mathcal {X}\) is finite dimensional, hence in finite dimensional case we do not need to distinguish these convergences. (Sequential cluster point) If a sequence \((x_n)_{n \in \mathbb {N}} \subset \mathcal {X}\) possesses a subsequence that strongly (weakly) converges to a point \(x \in \mathcal {X}\), then x is a strong (weak) sequential cluster point of \((x_n)_{n \in \mathbb {N}}\). For weak topology of real Hilbert space in the context of Hausdorff space, see [9, Lemma 2.30].
- 8.
- 9.
See [10, 42] for the history of the Douglas-Rachford splitting method, originated from Douglas-Rachford’s seminal paper [57] for solving matrix equations of the form u = Ax + Bx, where A and B are positive-definite matrices (see also [137]). For recent applications, of the Douglas-Rachford splitting method, to image recovery, see, e.g., [26, 40, 58, 60], and to data sciences, see, e.g., [38, 67, 68]. Lastly, we remark that it was shown in [61] that the alternating direction method of multipliers (ADMM) [17, 62, 66, 91, 150] can be seen as a dual variant of the Douglas-Rachford splitting method.
- 10.
- 11.
\(\ell _{+}^1\) denotes the set of all summable nonnegative sequences. \(\ell _{+}^2\) denotes the set of all square-summable nonnegative sequences.
- 12.
In [149, Sec. 17.5], the authors introduced briefly the central strategy of plugging the Douglas-Rachford splitting operator into the HSDM for hierarchical convex optimization. For applications of the HSDM to other proximal splitting operators, e.g., the forward-backward splitting operator [44], the primal-dual splitting operator [47, 139] for the hierarchical convex optimization of different types from (16.13), see [107, 149].
- 13.
- 14.
This question is common even for the soft margin SVM applied to the transformed data \(\mathfrak {D}\) employed in [16] because the linear separability of \(\mathfrak {D}\) is not always guaranteed.
- 15.
In terms of slack variables, Problem (16.147) can also be restated as

- 16.
If we need to guarantee \(\mathcal {S}_p\text{[in (16.13)]} \neq \varnothing \), we recommend the following slight modification of (16.147):
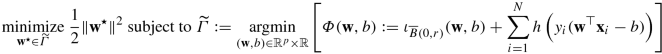
with a sufficiently large closed ball \(\overline {B}(0,r)\), where \(\mathcal {S}_p:=\widetilde {\varGamma } \neq \varnothing \) is guaranteed due to the coercivity of Φ. Fortunately, our strategies in Section 16.3 are still applicable to this modified problem because it is also an instance of (16.10) which can be translated into (16.13) as explained in Section 16.1. In the application of Theorem 16.17 in Section 16.3.1 to this modification, the boundedness of \(\operatorname {Fix}({\mathbf T}_{\text{DRS}_{\text{II}}})\) is automatically guaranteed because of Corollary 16.24(b) (see Section 16.3.3) and the boundedness of both \(\widetilde {\varGamma } \subset \overline {B}(0,r)\) and
 .
. - 17.
See footnote 16.
- 18.
References
Argyriou, A., Baldassarre, L., Micchelli, C.A., Pontil, M.: On sparsity inducing regularization methods for machine learning. In: B. Schölkopf, Z. Luo, V. Vovk (eds.) Empirical Inference, pp. 205–216. Springer Berlin, Heidelberg (2013)
Aronszajn, N.: Theory of reproducing kernels. Trans. Amer. Math. Soc. 68, 337–404 (1950)
Attouch, H.: Viscosity solutions of minimization problems. SIAM J. Optim. 6, 769–806 (1996)
Attouch, H., Cabot, A., Chbani, Z., Riahi, H.: Accelerated forward-backward algorithms with perturbations. Application to Tikhonov regularization. (preprint)
Baillon, J.-B., Bruck, R.E., Reich, S.: On the asymptotic behavior of nonexpansive mappings and semigroups in Banach spaces. Houst. J. Math. 4, 1–9 (1978)
Bauschke, H.H.: The approximation of fixed points of compositions of nonexpansive mappings in Hilbert space. J. Math. Anal. Appl. 202, 150–159 (1996)
Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38, 367–426 (1996)
Bauschke, H.H., Combettes, P.L.: A weak-to-strong convergence principle for Fejér monotone methods in Hilbert space. Math. Oper. Res. 26, 248–264 (2001)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Space, 2nd edn. Springer (2017)
Bauschke, H.H., Moursi, M.: On the Douglas-Rachford algorithm. Math. Program. 164, 263–284 (2017)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18, 2419–2434 (2009)
Ben-Israel, A., Greville, T.N.E.: Generalized Inverses: Theory and Applications, 2nd edn. Springer-Verlag (2003)
Bien, J., Gaynanova, I., Lederer, J., Müller, C.L.: Non-convex global minimization and false discovery rate control for the TREX. J. Comput. Graph. Stat. 27, 23–33 (2018)
Bishop, C.M.: Machine Learning and Pattern Recognition. Information Science and Statistics. Springer, Heidelberg (2006)
Blum, A., Rivest, R.L.: Training a 3-node neural network is NP-complete. Neural Networks 5, 117–127 (1992)
Boser, B.E., Guyon, I.M., Vapnik, V.N.: A training algorithm for optimal margin classifiers. In: Proc. the 5th Annual ACM Workshop on Computational Learning Theory (COLT), pp. 144–152 (1992)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 3, 1–122 (2011)
Cabot, A.: Proximal point algorithm controlled by a slowly vanishing term: Applications to hierarchical minimization. SIAM J. Optim. 15, 555–572 (2005)
Candler, W., Norton, R.: Multilevel programming. Technical Report 20, World Bank Development Research Center, Washington D.C., USA (1977)
Cegielski, A.: Iterative Methods for Fixed Point Problems in Hilbert Spaces. Springer (2012)
Censor, Y., Davidi, R., Herman, G.T.: Perturbation resilience and superiorization of iterative algorithms. Inverse Probl. 26, 065008 (2010)
Censor, Y., Zenios, S.A.: Parallel Optimization: Theory, Algorithm, and Optimization. Oxford University Press (1997)
Chaari, L., Ciuciu, P., Mériaux, S., Pesquet, J.C.: Spatio-temporal wavelet regularization for parallel MRI reconstruction: Application to functional MRI. Magn. Reson. Mater. Phys. Biol. Med. 27, 509–529 (2014)
Chambolle, A., Dossal, C.: On the convergence of the iterates of the “fast iterative shrinkage/thresholding algorithm”. J. Optim. Theory Appl. 166, 968–982 (2015)
Chang, C.C., Lin, C.J.: LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2, 1–27 (2011)
Chaux, C., Pesquet, J.C., Pustelnik, N.: Nested iterative algorithms for convex constrained image recovery problems. SIAM J. Imaging Sci. 2, 730–762 (2009)
Chidume, C.: Geometric Properties of Banach Spaces and Nonlinear Iterations (Chapter 7: Hybrid steepest descent method for variational inequalities). vol. 1965 of Lecture Notes in Mathematics. Springer (2009)
Chipman, J.S.: Linear restrictions, rank reduction, and biased estimation in linear regression. Linear Algebra Appl. 289, 55–74 (1999)
Chipman, J.S., Rao, M.M.: The treatment of linear restrictions in regression analysis. Econometrics 32, 198–204 (1964)
Coloson, B., Marcotte, P., Savard, G.: An overview of bilevel optimization. Ann. Oper. Res. 153, 235–256 (2007)
Combettes, P.L.: The foundations of set theoretic estimation. Proc. IEEE 81, 182–208 (1993)
Combettes, P.L.: Inconsistent signal feasibility problems: Least squares solutions in a product space. IEEE Trans. Signal Process. 42, 2955–2966 (1994)
Combettes, P.L.: Strong convergence of block-iterative outer approximation methods for convex optimization. SIAM J. Control Optim. 38, 538–565 (2000)
Combettes, P.L.: Iterative construction of the resolvent of a sum of maximal monotone operators. J. Convex Anal. 16, 727–748 (2009)
Combettes, P.L.: Perspective functions: Properties, constructions, and examples. Set-Valued Var. Anal. 26, 247–264 (2017)
Combettes, P.L., Bondon, P.: Hard-constrained inconsistent signal feasibility problems. IEEE Trans. Signal Process. 47, 2460–2468 (1999)
Combettes, P.L., Hirstoaga, S.A.: Approximating curves for nonexpansive and monotone operators. J. Convex Anal. 13, 633–646 (2006)
Combettes, P.L., Müller, C.L.: Perspective functions: Proximal calculus and applications in high-dimensional statistics. J. Math. Anal. Appl. 457, 1283–1306 (2018)
Combettes, P.L., Pesquet, J.-C.: Image restoration subject to a total variation constraint. IEEE Trans. Image Process. 13, 1213–1222 (2004)
Combettes, P.L., Pesquet, J.-C.: A Douglas-Rachford splitting approach to nonsmooth convex variational signal recovery. IEEE J. Sel. Top. Signal Process. 1, 564–574 (2007)
Combettes, P.L., Pesquet, J.-C.: A proximal decomposition method for solving convex variational inverse problems. Inverse Probl. 24, 065014 (2008)
Combettes, P.L., Pesquet, J.-C.: Proximal splitting methods in signal processing. In: H.H. Bauschke, R. Burachik, P. Combettes, V. Elser, D. Luke, H. Wolkowicz (eds.) Fixed-Point Algorithms for Inverse Problems in Science and Engineering, pp. 185–212. Springer-Verlag (2011)
Combettes, P.L., Pesquet, J.-C.: Stochastic quasi-Fejér block-coordinate fixed point iterations with random sweeping. SIAM J. Optim. 25, 1221–1248 (2015)
Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward-backward splitting. SIAM Multiscale Model. Simul. 4, 1168–1200 (2005)
Combettes, P.L., Yamada, I.: Compositions and convex combinations of averaged nonexpansive operators. J. Math. Anal. Appl. 425, 55–70 (2015)
Cominetti, R., Courdurier, M.: Coupling general penalty schemes for convex programming with the steepest descent and the proximal point algorithm. SIAM J. Optim. 13, 745–765 (2002)
Condat, L.: A primal-dual splitting method for convex optimization involving lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158, 460–479 (2013)
Cortes, C., Vapnik, V.N.: Support-vector networks. Mach. Learn. 20, 273–297 (1995)
Cover, T.M.: Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Trans. Electron. Comput. 14, 326–334 (1965)
Dalalyan, A.S., Hebiri, M., Lederer, J.: On the prediction performance of the Lasso. Bernoulli 23, 552–581 (2017)
Deutsch, F.: Best Approximation in Inner Product Spaces. New York: Springer-Verlag (2001)
Deutsch, F., Yamada, I.: Minimizing certain convex functions over the intersection of the fixed point sets of nonexpansive mappings. Numer. Funct. Anal. Optim. 19, 33–56 (1998)
Donoho, D.L.: De-noising by soft-thresholding. IEEE Trans. Inf. Theory 41, 613–627 (1995)
Donoho, D.L., Johnstone, I.M.: Ideal spatial adaptation via wavelet shrinkage. Biometrika 81, 425–455 (1994)
Dontchev, A.L., Zolezzi, T.: Well-posed optimization problems. vol. 1543 of Lecture Notes in Mathematics. Springer-Verlag (1993)
Dotson Jr., W.G.: On the Mann iterative process. Trans. Amer. Math. Soc. 149, 65–73 (1970)
Douglas, J., Rachford, H.H.: On the numerical solution of heat conduction problems in two or three space variables. Trans. Amer. Math. Soc. 82, 421–439 (1956)
Dupé, F.X., Fadili, M.J., Starck, J.-L.: A proximal iteration for deconvolving Poisson noisy images using sparse representations. IEEE Trans. Image Process. 18, 310–321 (2009)
Dupé, F.X., Fadili, M.J., Starck, J.-L.: Deconvolution under Poisson noise using exact data fidelity and synthesis or analysis sparsity priors. Stat. Methodol. 9, 4–18 (2012)
Durand, S., Fadili, M.J., Nikolova, M.: Multiplicative noise removal using L1 fidelity on frame coefficients. J. Math. Imaging Vision 36, 201–226 (2010)
Eckstein, J., Bertsekas, D.P.: On the Douglas-Rachford splitting method and proximal point algorithm for maximal monotone operators. Math. Program. 55, 293–318 (1992)
Eckstein, J., Yao, W.: Understanding the convergence of the alternating direction method of multipliers: Theoretical and computational perspectives. Pac. J. Optim. 11, 619–644 (2015)
Eicke, B.: Iteration methods for convexly constrained ill-posed problems in Hilbert space. Numer. Funct. Anal. Optim. 13, 413–429 (1992)
Ekeland, I., Themam, R.: Convex Analysis and Variational Problems. Classics in Applied Mathematics 28. SIAM (1999)
Fisher, A.R.: The use of multiple measurements in taxonomic problems. Ann. Hum. Genet. 7, 179–188 (1936)
Gabay, D.: Applications of the method of multipliers to variational inequalities. In: M. Fortin, R. Glowinski (eds.) Augmented Lagrangian Methods: Applications to the solution of boundary value problems. North-Holland, Amsterdam (1983)
Gandy, S., Recht, B., Yamada, I.: Tensor completion and low-n-rank tensor recovery via convex optimization. Inverse Probl. 27, 025010 (2011)
Gandy, S., Yamada, I.: Convex optimization techniques for the efficient recovery of a sparsely corrupted low-rank matrix. J. Math-For-Industry 2, 147–156 (2010)
van de Geer, S., Lederer, J.: The Lasso, correlated design, and improved oracle inequalities. IMS Collections 9, 303–316 (2013)
Goebel, K., Reich, S.: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. Marcel Dekker, New York (1984)
Groetsch, C. W.: A note on segmenting Mann iterates. J. Math. Anal. Appl. 40, 369–372 (1972)
Halpern, B.: Fixed points of nonexpanding maps. Bull. Amer. Math. Soc. 73, 957–961 (1967)
Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning, 2nd edn. Springer Series in Statistics (2009)
Hastie, T., Tibshirani, R., Wainwright, M.: Statistical Learning with Sparsity: The Lasso and Generalizations. CRC press (2015)
Haugazeau, Y.: Sur les inéquations variationnelles et la minimisation de fonctionnelles convexes. Thèse, Universite de Paris (1968)
He, B., Yuan, X.: On the O(1∕n) convergence rate of the Douglas-Rachford alternating direction method. SIAM J. Numer. Anal. 50, 700–709 (2012)
Hebiri, M., Lederer, J.: How correlations influence Lasso prediction. IEEE Trans. Inf. Theory 59, 1846–1854 (2013)
Helou, E.S., De Pierro, A.R.: On perturbed steepest descent methods with inexact line search for bilevel convex optimization. Optimization 60, 991–1008 (2011)
Helou, E.S., Simões, L.E.A.: 𝜖-subgradient algorithms for bilevel convex optimization. Inverse Probl. 33, 055020 (2017)
Herman, G.T., Gardu\(\tilde {n}\)o, E., Davidi, R., Censor, Y.: Superiorization: An optimization heuristic for medical physics. Med. Phys. 39, 5532–5546 (2012)
Hestenes, M.R.: Multiplier and gradient methods. J. Optim. Theory Appl. 4, 303–320 (1969)
Hiriart-Urruty, J.-B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms. Springer (1993)
Iemoto, S., Takahashi, W.: Strong convergence theorems by a hybrid steepest descent method for countable nonexpansive mappings in Hilbert spaces. Sci. Math. Jpn. 69, 227–240 (2009)
Judd, J.S.: Learning in networks is hard. In: Proc. 1st Int. Conf. Neural Networks, pp. 685–692 (1987)
Kailath, T., Sayed, A.H., Hassibi, B.: Linear Estimation. Prentice-Hall (2000)
Kitahara, D., Yamada, I.: Algebraic phase unwrapping based on two-dimensional spline smoothing over triangles. IEEE Trans. Signal Process. 64, 2103–2118 (2016)
Koltchinskii, V., Lounici, K., Tsybakov, A.: Nuclear-norm penalization and optimal rates for noisy low-rank matrix completion. Ann. Statist. 39, 2302–2329 (2011)
Krasnosel’skiı̆, M.A.: Two remarks on the method of successive approximations. Uspekhi Mat. Nauk 10, 123–127 (1955)
Lederer, J., Müller, C.L.: Don’t fall for tuning parameters: Tuning-free variable selection in high dimensions with the TREX. In: Proc. Twenty-Ninth AAAI Conf. Artif. Intell., pp. 2729–2735 (2015)
Lions, P.L.: Approximation de points fixes de contractions. C. R. Acad. Sci. Paris Sèrie A-B 284, 1357–1359 (1977)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)
Lobo, M.S., Vandenberghe, L., Boyd, S., Lebret, H.: Applications of second-order cone programming. Linear Algebra Appl. 284, 193–228 (1998)
Luenberger, D.G.: Optimization by Vector Space Methods. Wiley (1969)
Mainge, P.E.: Extension of the hybrid steepest descent method to a class of variational inequalities and fixed point problems with nonself-mappings. Numer. Funct. Anal. Optim. 29, 820–834 (2008)
Mangasarian, O.L.: Iterative solution of linear programs. SIAM J. Numer. Amal. 18, 606–614 (1981)
Mann, W.: Mean value methods in iteration. Proc. Amer. Math. Soc. 4, 506–510 (1953)
Marquardt, D.W.: Generalized inverses, ridge regression, biased linear estimation, and nonlinear estimation. Technometrics 12, 591–612 (1970)
Martinet, B.: Régularisation d’inéquations variationnelles par approximations successives. Rev. Française Informat. Recherche Opérationnelle 4, 154–159 (1970)
Martinet, B.: Détermination approchée d’un point fixe d’une application pseudo-contractante. C. R. Acad. Sci. Paris Ser. A-B 274, 163–165 (1972)
Moore, E.H.: On the reciprocal of the general algebraic matrix. Bull. Amer. Math. Soc. 26, 394–395 (1920)
Moreau, J.J.: Fonctions convexes duales et points proximaux dans un espace hilbertien. C. R. Acad. Sci. Paris Ser. A Math. 255, 2897–2899 (1962)
Moreau, J.J.: Proximité et dualité dans un espace hilbertien. Bull. Soc. Math. France 93, 273–299 (1965)
Nesterov, Y.: A method of solving a convex programming problem with convergence rate O(1∕k 2). Soviet Math. Dokl. 27, 372–376 (1983)
Nikazad, T., Davidi, R., Herman, G.T.: Accelerated perturbation-resilient block-iterative projection methods with application to image reconstruction. Inverse Probl. 28, 035005 (2012)
Ogura, N., Yamada, I.: Non-strictly convex minimization over the fixed point set of the asymptotically shrinking nonexpansive mapping. Numer. Funct. Anal. Optim. 23, 113–137 (2002)
Ogura, N., Yamada, I.: Non-strictly convex minimization over the bounded fixed point set of nonexpansive mapping. Numer. Funct. Anal. Optim. 24, 129–135 (2003)
Ono, S., Yamada, I.: Hierarchical convex optimization with primal-dual splitting. IEEE Trans. Signal Process. 63, 373–388 (2014)
Ono, S., Yamada, I.: Signal recovery with certain involved convex data-fidelity constraints. IEEE Trans. Signal Process. 63, 6149–6163 (2015)
Passty, G.B.: Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math. Anal. Appl. 72, 383–390 (1979)
Penfold, S.N., Schulte, R.W., Censor, Y., Rosenfeld, A.B.: Total variation superiorization schemes in proton computed tomography image reconstruction. Med. Phys. 37, 5887–5895 (2010)
Penrose, R.: A generalized inverse for matrices. Proc. Cambridge Philos. Soc. 51, 406–413 (1955)
Piotrowski, T., Cavalcante, R., Yamada, I.: Stochastic MV-PURE estimator? Robust reduced-rank estimator for stochastic linear model. IEEE Trans. Signal Process. 57, 1293–1303 (2009)
Piotrowski, T., Yamada, I.: MV-PURE estimator: Minimum-variance pseudo-unbiased reduced-rank estimator for linearly constrained ill-conditioned inverse problems. IEEE Trans. Signal Process. 56, 3408–3423 (2008)
Polyak, B.T.: Sharp minimum. International Workshop on Augmented Lagrangians (1979)
Potter, L.C., Arun, K.S.: A dual approach to linear inverse problems with convex constraints. SIAM J. Control Optim. 31, 1080–1092 (1993)
Powell, M.J.D.: A method for nonlinear constraints in minimization problems. In: R. Fretcher (ed.) Optimization, pp. 283–298. Academic Press (1969)
Pustelnik, N., Chaux, C., Pesquet, J.-C.: Parallel proximal algorithm for image restoration using hybrid regularization. IEEE Trans. Image Process. 20, 2450–2462 (2011)
Rao, C.R., Mitra, S.K.: Generalized Inverse of Matrices and Its Applications. John Wiley & Sons (1971)
Reich, S.: Weak convergence theorems for nonexpansive mappings in Banach spaces. J. Math. Anal. Appl. 67, 274–276 (1979)
Rigollet, P., Tsybakov, A.: Exponential screening and optimal rates of sparse estimation. Ann. Statist. 39, 731–771 (2011)
Rockafellar, R.T.: Monotone operators and proximal point algorithm. SIAM J. Control Optim. 14, 877–898 (1976)
Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis, 1st edn. Springer (1998)
Sabharwal, A., Potter, L.C.: Convexly constrained linear inverse problems: Iterative least-squares and regularization. IEEE Trans. Signal Process. 46, 2345–2352 (1998)
Saitoh, S.: Theory of Reproducing Kernels and Its Applications. Longman Scientific & Technical, Harlow (1988)
Schölkopf, B., Luo, Z., Vovk, V.: Empirical Inference. Springer-Verlag (2013)
Schölkopf, B., Smola, A.J.: Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT press (2002)
Solodov, M.: An explicit descent method for bilevel convex optimization. J. Convex Anal. 14, 227–237 (2007)
Solodov, M.: A bundle method for a class of bilevel nonsmooth convex minimization problems. SIAM J. Optim. 18, 242–259 (2008)
Takahashi, N., Yamada, I.: Parallel algorithms for variational inequalities over the cartesian product of the intersections of the fixed point sets of nonexpansive mappings. J. Approx. Theory 153, 139–160 (2008)
Takahashi, W.: Nonlinear Functional Analysis—Fixed Point Theory and its Applications. Yokohama Publishers (2000)
Theodoridis, S.: Machine Learning: Bayesian and Optimization Perspective. Academic Press (2015)
Tibshirani, R.: Regression shrinkage and selection via the Lasso. J. Roy. Statist. Soc. Ser. B 58, 267–288 (1996)
Tikhonov, A.N.: Solution of incorrectly formulated problems and the regularization method. Soviet Math. Dokl. 4, 1035–1038 (1963)
Tseng, P.: Applications of a splitting algorithm to decomposition in convex programming and variational inequalities. SIAM J. Control Optim. 29, 119–138 (1991)
Vapnik, V.N.: Statistical Learning Theory. John Wiley & Sons (1998)
Vapnik, V.N., Lerner, A.: Pattern recognition using generalized portrait method. Automat. Rem. Contr. 24, 774–780 (1963)
Varga, R.S.: Matrix Iterative Analysis, 2nd edn. Springer, New York (2000)
Vicente, L.N., Calamai, P.H.: Bilevel and multilevel programming: A bibliography review. J. Global Optim. 5, 291–306 (1994)
Vu, B.C.: A splitting algorithm for dual monotone inclusions involving cocoercive operators. Adv. Comput. Math. 38, 667–681 (2013)
Xu, H.K., Kim, T.H.: Convergence of hybrid steepest descent methods for variational inequalities. J. Optim. Theory Appl. 119, 185–201 (2003)
Yamada, I.: Approximation of convexly constrained pseudoinverse by hybrid steepest descent method. In: Proc. IEEE ISCAS (1999)
Yamada, I.: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In: D. Butnariu, Y. Censor, S. Reich (eds.) Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, pp. 473–504. Elsevier (2001)
Yamada, I.: Kougaku no Tameno Kansu Kaiseki (Functional Analysis for Engineering). Suurikougaku-Sha/Saiensu-Sha, Tokyo (2009)
Yamada, I., Elbadraoui, J.: Minimum-variance pseudo-unbiased low-rank estimator for ill-conditioned inverse problems. In: Proc. IEEE ICASSP, III, pp. 325–328 (2006)
Yamada, I., Ogura, N.: Hybrid steepest descent method for variational inequality problem over the fixed point set of certain quasi-nonexpansive mappings. Numer. Funct. Anal. Optim. 25, 619–655 (2004)
Yamada, I., Ogura, N., Shirakawa, N.: A numerically robust hybrid steepest descent method for the convexly constrained generalized inverse problems. In: Z. Nashed, O. Scherzer (eds.) Inverse Problems, Image Analysis, and Medical Imaging, Contemporary Mathematics, vol. 313, pp. 269–305. AMS (2002)
Yamada, I., Ogura, N., Yamashita, Y., Sakaniwa, K.: An extension of optimal fixed point theorem for nonexpansive operator and its application to set theoretic signal estimation. Technical Report of IEICE, DSP96-106, pp. 63–70 (1996)
Yamada, I., Ogura, N., Yamashita, Y., Sakaniwa, K.: Quadratic optimization of fixed points of nonexpansive mappings in Hilbert space. Numer. Funct. Anal. Optim. 19, 165–190 (1998)
Yamada, I., Yukawa, M., Yamagishi, M.: Minimizing the Moreau envelope of nonsmooth convex functions over the fixed point set of certain quasi-nonexpansive mappings. In: H.H. Bauschke, R. Burachik, P. Combettes, V. Elser, D. Luke, H. Wolkowicz (eds.) Fixed-Point Algorithms for Inverse Problems in Science and Engineering, pp. 345–390. Springer (2011)
Yamagishi, M., Yamada, I.: Nonexpansiveness of a linearized augmented Lagrangian operator for hierarchical convex optimization. Inverse Probl. 33, 044003 (2017)
Yang, J., Yuan, X.: Linearized augmented Lagrangian and alternating direction methods for nuclear norm minimization. Math. Comp. 82, 301–329 (2013)
Zălinescu, C.: Convex Analysis in General Vector Spaces. World Scientific (2002)
Zeidler, E.: Nonlinear Functional Analysis and its Applications, III - Variational Methods and Optimization. Springer (1985)
Acknowledgements
Isao Yamada would like to thank Heinz H. Bauschke, D. Russell Luke, and Regina S. Burachik for their kind encouragement and invitation of the first author to the dream meeting: Splitting Algorithms, Modern Operator Theory, and Applications (September 17–22, 2017) in Oaxaca, Mexico where he had a great opportunity to receive insightful deep comments by Hédy Attouch. He would also like to thank Patrick Louis Combettes and Christian L. Müller for their invitation of the first author to a special mini-symposium Proximal Techniques for High-Dimensional Statistics in the SIAM conference on Optimization 2017 (May 22–25, 2017) in Vancouver. Their kind invitations and their excellent approach to the TREX problem motivated very much the authors to study the application of the proposed strategies to the hierarchical enhancement of Lasso in this paper. Isao Yamada would also like to thank Raymond Honfu Chan for his kind encouragement and invitation to the Workshop on Optimization in Image Processing (June 27–30, 2016) at the Harvard University. Lastly, the authors thank to Yunosuke Nakayama for his help in the numerical experiment related to the proposed hierarchical enhancement of the SVM.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendices
16.1.1 A: Proof of Proposition 16.9(a)
Fact 16.5(i)⇔(ii) in Section 16.2.1 yields

The remaining follows from the proof in [40, Proposition 18]. □
16.1.2 B: Proof of Proposition 16.10(a)(d)
(a) From (16.58) and (16.59), there exists \((x_{\star },\nu _{\star }) \in \mathcal {S}_{\text{pLAL}} \times \mathcal {S}_{\text{dLAL}}\). Fact 16.5(i)⇔(ii) in Section 16.2.1 yields the equivalence



□
(d) Choose arbitrarily \((\bar {x},\bar {\nu }) \in \operatorname {Fix}(T_{\text{LAL}})\), i.e.,

Let \((x_n,\nu _n)_{n \in \mathbb {N}} \subset \mathcal {X} \times \mathcal {K}\) be generated, with any \((x_0,\nu _0) \in \mathcal {X} \times \mathcal {K}\), by

Then [150, (B.3)] yields

Equation (16.179) and ∥A∥op < 1 imply that \((\|x_n-\bar {x} \|{ }_{\mathcal {X}}^2 +\|\nu _n-\bar {\nu } \|{ }_{\mathcal {K}}^2)_{n \in \mathbb {N}}\) decreases monotonically, i.e., \((x_{n},\nu _n)_{n \in \mathbb {N}}\) is Fejér monotone with respect to \(\operatorname {Fix}(T_{\text{LAL}})\), and \((\|x_n-\bar {x} \|{ }_{\mathcal {X}}^2 +\|\nu _n-\bar {\nu } \|{ }_{\mathcal {K}}^2)_{n \in \mathbb {N}}\) converges to some c ≥ 0. From this observation, we have

and thus

By [51, Theorem 9.12], the bounded sequence of \((x_n,\nu _n)_{n \in \mathbb {N}}\) has some subsequence \((x_{n_j},\nu _{n_j})_{j \in \mathbb {N}}\) which converges weakly to some point, say (x ⋆, ν ⋆), in the Hilbert space \(\mathcal {X} \times \mathcal {K}\). Therefore, by applying [9, Theorem 9.1(iii)⇔(i)] to \(f \in \varGamma _0(\mathcal {X})\), we have

and, by the Cauchy-Schwarz inequality and (16.180),

which implies Ax ⋆ = 0.
Meanwhile, by (16.178), we have

where the inner product therein satisfies

which is verified by Ax ⋆ = 0, the triangle inequality, the Cauchy-Schwarz inequality, and (16.180), as follows:

Now, by (16.182), (16.181), and (16.183), we have for any \( x \in \mathcal {X}\)

which implies
By recalling (16.176)⇔(16.177), (16.184) and Ax ⋆ = 0 prove \((x_{\star }, \nu _{\star }) \in \operatorname {Fix}(T_{\text{LAL}})\). The above discussion implies that every weak sequential cluster point (see Footnote 7 in Section 16.2.2) of \((x_n,\nu _n)_{n \in \mathbb {N}}\), which is Fejér monotone with respect to \(\operatorname {Fix}(T_{\text{LAL}})\), belongs to \(\operatorname {Fix}(T_{\text{LAL}})\). Therefore, [9, Theorem 5.5] guarantees that \((x_n,\nu _n)_{n \in \mathbb {N}}\) converges weakly to a point in \(\operatorname {Fix}(T_{\text{LAL}})\). □
16.1.3 C: Proof of Theorem 16.15
Now by recalling Proposition 16.9 in Section 16.2.3 and Remark 16.16 in Section 16.3.1, it is sufficient to prove Claim 16.15. Let \(x_{\star } \in \mathcal {S}_p \neq \varnothing \). Then the Fermat’s rule, Fact 16.4(b) (applicable due to the qualification condition (16.40)) in Section 16.2.1, \(\check {A}^*\colon \mathcal {K} \to \mathcal {X} \times \mathcal {K}\colon \nu \mapsto (A^*\nu , -\nu )\) for \(\check {A}\) in (16.74), the property of ι {0} in (16.35), the straightforward calculations, and Fact 16.5(ii)⇔(i) (in Section 16.2.1) yield

which confirms Claim 16.15. □
16.1.4 D: Proof of Theorem 16.17
Now by recalling Proposition 16.9 in Section 16.2.3 and Remark 16.18 in Section 16.3.1, it is sufficient to prove (16.97) by verifying Claim 16.17. We will use
which is verified by \(g=\bigoplus _{i=1}^mg_i\), Fact 16.4(c) (see Section 16.2.1), and \(\operatorname {ri}(\operatorname {dom}(g_j) - \operatorname {ran}(A_j))=\operatorname {ri}(\operatorname {dom}(g_j) - \mathbb {R})=\mathbb {R} \ni 0\) (j = 1, 2, …, m). Let \(x_{\star }^{(m+1)} \in \mathcal {S}_p \neq \varnothing \). Then by using the Fermat’s rule, Fact 16.4(b) (applicable due to (16.40)), (16.185), D in (16.93), and H in (16.92), we deduce the equivalence

Then by \(-\begin {pmatrix} \nu ^{(1)}, \ldots , \nu ^{(m)}, -\sum _{i=1}^m \nu ^{(i)} \end {pmatrix} \in D^{\perp }=\partial \iota _{D}(x_{\star }^{(1)},\ldots ,x_{\star }^{(m+1)})\) (see (16.34) ) and by Fact 16.5(ii)⇔(i) in Section 16.2.1, we have

which confirms Claim 16.17. □
16.1.5 E: Proof of Theorem 16.19
Now by recalling Proposition 16.10 in Section 16.2.3 and Remark 16.20 in Section 16.3.2, it is sufficient to prove Claim 16.19. Let \(x_{\star } \in \mathcal {S}_p \neq \varnothing \). Then the Fermat’s rule, Fact 16.4(b) (applicable due to (16.40)) in Section 16.2.1, \(\check {A}^*\colon \mathcal {K} \to \mathcal {X} \times \mathcal {K}\colon \nu \mapsto (A^*\nu , -\nu )\) for \(\check {A}\) in (16.74), the property of ι {0} in (16.35), the straightforward calculations, and Fact 16.5(ii)⇔(i) (in Section 16.2.1) yield

which confirms Claim 16.19. □
16.1.6 F: Proof of Theorem 16.23
-
(a)
We have seen in (16.78) that, under the assumptions of Theorem 16.23(a), for any vector \(x_{\star } \in \mathcal {X}\),
 (16.187)
(16.187)for some \(y_{\star } \in \mathcal {X}\) and some \({\mathbf \zeta }_{\star } \in \operatorname {Fix}\left ({\mathbf T}_{\text{DRS}_{\text{I}}}\right )\), where \(\check {A}\colon \mathcal {X} \times \mathcal {K} \to \mathcal {K}\colon (x,y) \mapsto Ax-y\) (see (16.74)), \(\mathcal {N}(\check {A})=\{(x,Ax) \in \mathcal {X} \times \mathcal {K}\mid x \in \mathcal {X} \}\), and \({\mathbf T}_{\text{DRS}_{\text{I}}}=(2\operatorname {prox}_F -\text{I}) \circ (2{P}_{\mathcal {N}(\check {A})} -\text{I})\) for \(F\colon \mathcal {X} \times \mathcal {K} \to (-\infty ,\infty ]\colon (x,y)\mapsto f(x)+g(y)\) (see (16.71) and (16.73)).
Choose \({\mathbf \zeta }_{\star }:=(\zeta ^x_{\star }, \zeta ^y_{\star }) \in \operatorname {Fix}\left ({\mathbf T}_{\text{DRS}_{\text{I}}}\right )\) arbitrarily and let \({\mathbf z}_{\star }:=(x_{\star }, y_{\star }) := {P}_{\mathcal {N}(\check {A})}({\mathbf \zeta }_{\star })\). Then we have
 (16.188)
(16.188) (16.189)
(16.189) (16.190)
(16.190)Meanwhile, we have
 (16.191)
(16.191)Equations (16.191) and (16.190) imply
 (16.192)
(16.192)Moreover, by noting that (16.187) ensures \(x_{\star } \in \mathcal {S}_p\) and y ⋆ = Ax ⋆, we have from (16.192)

Since ζ ⋆ is chosen arbitrarily from \(\operatorname {Fix}\left ({\mathbf T}_{\text{DRS}_{\text{I}}}\right )\), we have
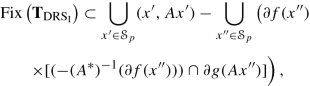 (16.193)
(16.193)from which Theorem 16.23(a) is confirmed.
-
(b)
We have seen in (16.113) that, under the assumptions of Theorem 16.23(b), for any vector \(x_{\star } \in \mathcal {X}\),
 (16.194)
(16.194)for some \((y_{\star },\nu _{\star }) \in \mathcal {K} \times \mathcal {K}\), where

and \((\mathfrak {u} \check {A})^*\colon \mathcal {K} \to \mathcal {X} \times \mathcal {K}\colon \nu \mapsto (\mathfrak {u}A^* \nu , -\mathfrak {u} \nu )\) (see (16.108) and (16.120)).
Choose \(({\mathbf z}_{\star }, \nu _{\star }) \in \operatorname {Fix}({\mathbf T}_{\text{LAL}})\) arbitrarily and denote \({\mathbf z}_{\star }=(x_{\star },y_{\star }) \in \mathcal {X} \times \mathcal {K}\). By passing similar steps in (16.177)⇔(16.176), we deduce
 (16.195)
(16.195)and then, from (16.195), straightforward calculations yield
 (16.196)
(16.196)Moreover, by noting that (16.194), we have from (16.196)
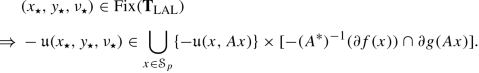
Since (x ⋆, y ⋆, ν ⋆) is chosen arbitrarily from \( \operatorname {Fix}({\mathbf T}_{\text{LAL}})\), we have

from which Theorem 16.23(b) is confirmed.
-
(c)
We have seen in (16.98) that, under the assumptions of Theorem 16.23(c), for any vector \(x_{\star } \in \mathcal {X}\),
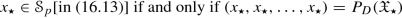 (16.197)
(16.197)for some \( \mathfrak {X}_{\star } \in \operatorname {Fix}\left ({\mathbf T}_{\text{DRS}_{\text{II}}}\right )\), where \(D= \{(x^{(1)},\ldots ,x^{(m+1)}) \in \mathcal {X}^{m+1} \mid x^{(i)}=x^{(j)} \ (i,j =1,2,\ldots , m+1) \}\) (see (16.93)), \(H\colon \mathcal {X}^{m+1} \to (-\infty ,\infty ]\colon (x^{(1)},\ldots ,x^{(m+1)}) \mapsto \sum _{i=1}^m g_i(A_ix^{(i)})+f(x^{(m+1)})\) (see (16.92)), and \({\mathbf T}_{\text{DRS}_{\text{II}}}=(2\operatorname {prox}_H -\text{I}) \circ (2{P}_{D} -\text{I})\) (see (16.90)) [For the availability of \(\operatorname {prox}_H\) and P D as computational tools, see Remark 16.18(a)].
Choose \(\mathfrak {X}_{\star }:=(\zeta _{\star }^{(1)},\ldots , \zeta _{\star }^{(m+1)}) \in \operatorname {Fix}\left ({\mathbf T}_{\text{DRS}_{\text{II}}}\right )\) arbitrarily, and let \({\mathbf X}_{\star }:=(x_{\star }, \ldots , x_{\star }) = {P}_D(\mathfrak {X}_{\star })\). Then we have
 (16.198)
(16.198)Now, by passing similar steps for (16.188)⇒(16.189), we deduce that
 (16.199)
(16.199)where the last equivalence follows from Fact 16.4(c) (applicable due to \(\operatorname {ri}(\operatorname {dom}(g_j) - \operatorname {ran}(A_j))=\operatorname {ri}(\operatorname {dom}(g_j) - \mathbb {R})=\mathbb {R} \ni 0\)). Meanwhile, we have
 (16.200)
(16.200)Equations (16.200) and (16.199) imply
 (16.201)
(16.201)Moreover, by noting that (16.197) ensures \(x_{\star } \in \mathcal {S}_p\), we have from (16.201)

Since \(\mathfrak {X}_{\star }\) is chosen arbitrarily from \(\operatorname {Fix}({\mathbf T}_{\text{DRS}_{\text{II}}})\), we have
 (16.202)
(16.202)from which Theorem 16.23(c) is confirmed. □
16.1.7 G: Proof of Lemma 16.27
Obviously, we have from (16.158)

By recalling \(0 \neq {\mathbf x}_{j} \in \mathbb {R}^{N}\text{ in (16.153)}\) and \({\mathbf M}_{j} \in \mathbb {R}^{(N+1) \times p}\) in (16.159), we have

and therefore

To prove \(\operatorname {dom}(g_{(j,q)}) - {\mathbf M}_j\operatorname {dom}(\|\cdot \|{ }_1)=\mathbb {R} \times \mathbb {R}^N\), choose arbitrarily \((\eta , {\mathbf y}) \in \mathbb {R} \times \mathbb {R}^N\). Then (16.203) and (16.204) guarantee

implying thus

□
16.1.8 H: Proof of Theorem 16.28
By recalling Remark 16.29 in Section 16.5.2, it is sufficient to prove Claim 16.28, for which we use the following inequality: for each j = 1, 2, …, 2p,

where \({\mathbf x}_j \in \mathbb {R}^{N}\) in (16.153) and \({\mathbf M}_j \in \mathbb {R}^{(N+1) \times p}\) in (16.159). Equation (16.206) is confirmed by

and

Let \(U_S:=\sup \{\|{\mathbf b}\| \mid {\mathbf b} \in S\}(<\infty )\). By supercoercivity of φ and Example 16.3, the subdifferential of its perspective \(\widetilde {\varphi }\) at each \((\eta , {\mathbf y}) \in \mathbb {R} \times \mathbb {R}^N\) can be expressed as (16.32), and thus, to prove Claim 16.28, it is sufficient to show

Proof of (i)
Choose \((\eta ,{\mathbf y}) \in \mathbb {R}_{++} \times \mathbb {R}^{N}\) arbitrarily. Then, from (16.32), every \({\mathbf c}_{(\eta ,{\mathbf y})} \in ({\mathbf M}_j^{\top })^{-1}(S) \cap \partial \widetilde {\varphi }(\eta ,{\mathbf y}) \subset \mathbb {R} \times \mathbb {R}^{N}\) can be expressed with some u ∈ ∂φ(y∕η) as
where the last equality follows from φ(y∕η) + φ ∗(u) = 〈y∕η, u〉 due to the Fenchel-Young identity (16.30). By \({\mathbf M}_j^{\top }{\mathbf c}_{(\eta ,{\mathbf y})} \in S\) and by applying the inequality (16.206) to (16.208), we have

where  and
and  are coercive convex functions (see Section 16.2.1) and independent from the choice of (η, y). The coercivity of
are coercive convex functions (see Section 16.2.1) and independent from the choice of (η, y). The coercivity of  ensures the existence of an open ball \(B(0,\hat {U}_{\text{(i)}})\) of radius \(\hat {U}_{\text{(i)}}>0\) such that
ensures the existence of an open ball \(B(0,\hat {U}_{\text{(i)}})\) of radius \(\hat {U}_{\text{(i)}}>0\) such that  , and thus (16.209) implies
, and thus (16.209) implies

Moreover, by x j ≠ 0, the triangle inequality, the Cauchy-Schwarz inequality, (16.209), and (16.210), we have

which yields \({\mathbf c}_{(\eta ,{\mathbf y})}=(- \varphi ^*({\mathbf u}), {\mathbf u}) \in [-U_{\text{(i)}}, {U}_{\text{(i)}}] \times B(0,\hat {U}_{\text{(i)}} )\). Since \((\eta ,{\mathbf y})\in \mathbb {R}_{++} \times \mathbb {R}^{N}\) is chosen arbitrarily and \({\mathbf c}_{(\eta ,{\mathbf y})} \in ({\mathbf M}_j^{\top })^{-1}(S) \cap \partial \widetilde {\varphi }(\eta ,{\mathbf y})\) is also chosen arbitrarily, we have

which confirms the statement (i).
Proof of (ii)
By introducing
we can decompose the set \(({\mathbf M}_j^{\top })^{-1}(S) \cap \partial \widetilde {\varphi }(0,0)\) into

In the following, we show the boundedness of each set in (16.213).
First, we show the boundedness of \(\mathfrak {B}\) by contradiction. Suppose that \(\mathfrak {B} \not \subset B(0,r)\) for all r > 0. Then there exists a sequence \(({\mathbf u}_k)_{k \in \mathbb {N}} \subset \mathbb {R}^N\) such that

which contradicts the supercoercivity of φ ∗, implying thus the existence of r ∗ > 0 such that \(\mathfrak {B} \subset B(0,r_*)\).
Next, we show the boundedness of the former set in (16.213). Choose arbitrarily

By x j ≠ 0, \({\mathbf M}_j^{\top } (\mu ,{\mathbf u}^{\top })^{\top } \in S \subset B(0,U_S)\), the inequality (16.206), the triangle inequality, the Cauchy-Schwarz inequality, and \({\mathbf u} \in \mathfrak {B} \subset B(0,r_*)\), we have

which yields

Therefore, we have \((\mu ,{\mathbf u}) \in [-\hat {U}_{\text{(iia)}}, \hat {U}_{\text{(iia)}}] \times B(0,r_{\star })\). Since \((\mu ,{\mathbf u}) \in ({\mathbf M}_j^{\top })^{-1}(S) \cap \partial \widetilde {\varphi }(0,0) \cap (\mathbb {R} \times \mathfrak {B})\) is chosen arbitrarily, we have

Finally, we show the boundedness of the latter set in (16.213). Let

From (16.32), we have

Note that coercivity of φ ∗ (\(\Rightarrow \exists \min \varphi ^*(\mathbb {R}^N) \in \mathbb {R}\), see Fact 16.2) and (16.218) yield \(\varphi ^*({\mathbf u}) \in [\min \varphi ^*(\mathbb {R}^N), -\mu ]\) and thus
By x j ≠ 0, \({\mathbf M}_j^{\top } (\mu ,{\mathbf u}^{\top })^{\top } \in S \subset B(0,U_S)\) (see (16.217)), the inequality (16.206), the triangle inequality, \({\mathbf u} \in \mathfrak {B}^c\) (see (16.217) and (16.212)), and (16.219), we have

and thus, with (16.219),

Hence, we have

Since \((\mu ,{\mathbf u}) \in ({\mathbf M}_j^{\top })^{-1}(S) \cap \partial \widetilde {\varphi }(0,0)\cap (\mathbb {R} \times \mathfrak {B}^c)\) is chosen arbitrarily, we have

Consequently, by using (16.216) and (16.221) and by letting \(U_{\text{(ii)}}:=\max \{\hat {U}_{\text{(iia)}},\hat {U}_{\text{(iib)}} \}\), we have

which guarantees the boundedness of \(({\mathbf M}_j^{\top })^{-1}(S) \cap \partial \widetilde {\varphi }(0,0)\), due to the coercivity of φ ∗, implying thus finally the statement (ii).
□
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Yamada, I., Yamagishi, M. (2019). Hierarchical Convex Optimization by the Hybrid Steepest Descent Method with Proximal Splitting Operators—Enhancements of SVM and Lasso. In: Bauschke, H., Burachik, R., Luke, D. (eds) Splitting Algorithms, Modern Operator Theory, and Applications. Springer, Cham. https://doi.org/10.1007/978-3-030-25939-6_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-25939-6_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25938-9
Online ISBN: 978-3-030-25939-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



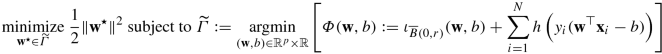
 .
.