Synthesis of Symbolic Controllers: A Parallelized and Sparsity-Aware Approach

Abstract

The correctness of control software in many safety-critical applications such as autonomous vehicles is very crucial. One approach to achieve this goal is through “symbolic control”, where complex physical systems are approximated by finite-state abstractions. Then, using those abstractions, provably-correct digital controllers are algorithmically synthesized for concrete systems, satisfying some complex high-level requirements. Unfortunately, the complexity of constructing such abstractions and synthesizing their controllers grows exponentially in the number of state variables in the system. This limits its applicability to simple physical systems.

This paper presents a unified approach that utilizes sparsity of the interconnection structure in dynamical systems for both construction of finite abstractions and synthesis of symbolic controllers. In addition, parallel algorithms are proposed to target high-performance computing (HPC) platforms and Cloud-computing services. The results show remarkable reductions in computation times. In particular, we demonstrate the effectiveness of the proposed approach on a 7-dimensional model of a BMW 320i car by designing a controller to keep the car in the travel lane unless it is blocked.

This work was supported in part by the H2020 ERC Starting Grant AutoCPS and the U.S. National Science Foundation grant CNS-1446145.

1 Introduction

Recently, the world has witnessed many emerging safety-critical applications such as smart buildings, autonomous vehicles and smart grids. These applications are examples of cyber-physical systems (CPS). In CPS, embedded control software plays a significant role by monitoring and controlling several physical variables, such as pressure or velocity, through multiple sensors and actuators, and communicates with other systems or with supporting computing servers. A novel approach to design provably correct embedded control software in an automated fashion, is via formal method techniques [10, 11], and in particular symbolic control.

Symbolic control provides algorithmically provably-correct controllers based on the dynamics of physical systems and some given high-level requirements. In symbolic control, physical systems are approximated by finite abstractions and then discrete (a.k.a. symbolic) controllers are automatically synthesized for those abstractions, using automata-theoretic techniques [5]. Finally, those controllers will be refined to hybrid ones applicable to the original physical systems. Unlike traditional design-then-test workflows, merging design phases with formal verification ensures that controllers are certified-by-construction. Current implementations of symbolic control, unfortunately, take a monolithic view of systems, where the entire system is modeled, abstracted, and a controller is synthesized from the overall state sets. This view interacts poorly with the symbolic approach, whose complexity grows exponentially in the number of state variables in the model. Consequently, the technique is limited to small dynamical systems.

1.1 Related Work

Recently, two promising techniques were proposed for mitigating the computational complexity of symbolic controller synthesis. The first technique [2] utilizes sparsity of internal interconnection of dynamical systems to efficiently construct their finite abstractions. It is only presented for constructing abstractions while controller synthesis is still performed monolithically without taking into account the sparse structure. The second technique [4] provides parallel algorithms targeting high performance (HPC) computing platforms, but suffers from state-explosion problem when the number of parallel processing elements (PE) is fixed. We briefly discuss each of those techniques and propose an approach that efficiently utilizes both of them.

Many abstraction techniques implemented in existing tools, including SCOTS [9], traverse the state space in a brute force way and suffer from an exponential runtime with respect to the number of state variables. The authors of [2] note that a majority of continuous-space systems exhibit a coordinate structure, where the governing equation for each state variable is defined independently. When the equations depend only on a few continuous variables, then they are said to be sparse. They proposed a modification to the traditional brute-force procedure to take advantage of such sparsity only in constructing abstractions. Unfortunately, the authors do not leverage sparsity to improve synthesis of symbolic controllers, which is, practically, more computationally complex. In this paper, we propose a parallel implementation of their technique to utilize HPC platforms. We also show how sparsity can be utilized, using a parallel implementation, during the controller synthesis phase as well.

The framework pFaces [4] is introduced as an acceleration ecosystem for implementations of symbolic control techniques. Parallel implementations of the abstraction and synthesis algorithms are introduced as computation kernels in pFaces, which are were originally done serially in SCOTS [9]. The proposed algorithms treat the problem as a data-parallel task and they scale remarkably well as the number of PEs increases. pFaces allows controlling the complexity of symbolic controller synthesis by adding more PEs. The results introduced in [4] outperform all exiting tools for abstraction construction and controller synthesis. However, for a fixed number of PEs, the algorithms still suffer from the state-explosion problem.

In this paper, we propose parallel algorithms that utilize the sparsity of the interconnection in the construction of abstraction and controller synthesis. In particular, the main contributions of this paper are twofold:

• (1) We introduce a parallel algorithm for constructing abstractions with a distributed data container. The algorithm utilizes sparsity and can run on HPC platforms. We implement it in the framework of pFaces and it shows remarkable reduction in computation time compared to the results in [2].

• (2) We introduce a parallel algorithm that integrates sparsity of dynamical systems into the controller synthesis phase. Specifically, a sparsity-aware preprocessing step concentrates computational resources in a small relevant subset of the state-input space. This algorithm returns the same result as the monolithic procedure, while exhibiting lower runtimes. To the best of our knowledge, the proposed algorithm is the first to merge parallelism with sparsity in the context of symbolic controller synthesis.

2 Preliminaries

Given two sets A and B, we denote by $\vert A \vert$ the cardinality of A, by $2^A$ the set of all subsets of A, by $A \times B$ the Cartesian product of A and B, and by $A \setminus B$ the Pontryagin difference between the sets A and B. Set $\mathbb {R}^n$ represents the n-dimensional Euclidean space of real numbers. This symbol is annotated with subscripts to restrict it in the obvious way, e.g., $\mathbb {R}^n_+$ denotes the positive (component-wise) n-dimensional vectors. We denote by $\pi _A : A \times B \rightarrow A$ the natural projection map on A and define it, for a set $C \subseteq A \times B$, as follows: $\pi _A(C) = \{ a \in A \;\vert \; \exists _{b \in B} \; (a,b) \in C \}$. Given a map $R: A \rightarrow B$ and a set $\mathcal {A} \subseteq A$, we define $R(\mathcal {A}) := \mathop {\bigcup }\limits _{a \in \mathcal {A}} \{R(a)\}$. Similarly, given a set-valued map $Z: A \rightarrow 2^B$ and a set $\mathcal {A} \subseteq A$, we define .

We consider general discrete-time nonlinear dynamical systems given in the form of the update equation:

$$\begin{aligned} \varSigma : x^+ = f(x,u), \end{aligned}$$

(1)

where $x \in X \subseteq \mathbb {R}^n$ is a state vector and $u \in U \subseteq \mathbb {R}^m$ is an input vector. The system is assumed to start from some initial state $x(0) = x_0 \in X$ and the map f is used to update the state of the system every $\tau$ seconds. Let set $\bar{X}$ be a finite partition on X constructed by a set of hyper-rectangles of identical widths $\eta$ $\in \mathbb {R}_{+}^n$ and let set $\bar{U}$ be a finite subset of U. A finite abstraction of (1) is a finite-state system $\bar{\varSigma } = (\bar{X},\bar{U},T)$, where $T \subseteq \bar{X}\times \bar{U}\times \bar{X}$ is a transition relation crafted so that there exists a feedback-refinement relation (FRR) $\mathcal {R} \subseteq X \times \bar{X}$ from $\varSigma$ to $\bar{\varSigma }$. Interested readers are referred to [8] for details about FRRs and their usefulness on synthesizing controllers for concrete systems using their finite abstractions.

Fig. 1.

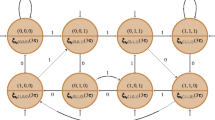
The sparsity graph of the vehicle example as introduced in [2].

For a system $\varSigma$, an update-dependency graph is a directed graph of verticies representing input variables $\{u_1,u_2,\cdots ,u_m\}$, state variables $\{x_1,x_2,\cdots ,x_n\}$, and updated state variables $\{x^+_1,x^+_2,\cdots ,x^+_n\}$, and edges that connect input (resp. states) variables to the affected updated state variables based on map f. For example, Fig. 1 depicts the update-dependency graph of the vehicle case-study presented in [2] with the update equation:

$$\begin{aligned} \begin{bmatrix} x^+_1\\ x^+_2\\ x^+_3 \end{bmatrix} = \begin{bmatrix} f_1(x_1,x_3,u_1,u_2)\\ f_2(x_2,x_3,u_1,u_2)\\ f_3(x_3,u_1,u_2) \end{bmatrix}, \end{aligned}$$

for some nonlinear functions $f_1,f_2$, and $f_3$. The state variable $x_3$ affects all updated state variables $x^+_1$, $x^+_2$, and $x^+_3$. Hence, the graph has edges connecting $x_3$ to $x^+_1$, $x^+_2$, and $x^+_3$, respectively. As update-dependency graphs become denser, sparsity of their corresponding abstract systems is reduced. The same graph applies to the abstract system $\bar{\varSigma }$.

We sometimes refer to $\bar{X}$, $\bar{U}$, and T as monolithic state set, monolithic input set and monolithic transition relation, respectively. A generic projection map

$$\begin{aligned} P^f_i : A \rightarrow \pi ^i(A) \end{aligned}$$

is used to extract elements of the corresponding subsets affecting the updated state $\bar{x}^+_i$. Note that $A \subseteq \bar{X} := \bar{X}_1 \times \bar{X}_2 \times \cdots \times \bar{X}_n$ when we are interested in extracting subsets of the state set and $A \subseteq \bar{U} := \bar{U}_1 \times \bar{U}_2 \times \cdots \times \bar{U}_m$ when we are interested in extracting subsets of the input set. When extracting subsets of the state set, $\pi ^i$ is the projection map $\pi _{\bar{X}_{k_1} \times \bar{X}_{k_2} \times \cdots \times \bar{X}_{k_K}}$, where $k_j \in \{1,2,\cdots ,n\}$, $j \in \{1,2,\cdots ,K\}$, and $\bar{X}_{k_1} \times \bar{X}_{k_2} \times \cdots \times \bar{X}_{k_K}$ is a subset of states affecting the updated state variable $\bar{x}^+_i$. Similarly, when extracting subsets of the input set, $\pi ^i$ is the projection map $\pi _{\bar{U}_{p_1} \times \bar{U}_{p_2} \times \cdots \times \bar{U}_{p_P}}$, where $p_i \in \{1,2,\cdots ,m\}$, $i \in \{1,2,\cdots ,P\}$, $\bar{U}_{p_1} \times \bar{U}_{p_2} \times \cdots \times \bar{U}_{p_P}$ is a subset of inputs affecting the updated state variable $\bar{x}^+_i$.

For example, assume that the monolithic state (resp. input) set of the system $\bar{\varSigma }$ in Fig. 1 is given by $\bar{X} := \bar{X}_1 \times \bar{X}_2 \times \bar{X}_3$ (resp. $\bar{U} := \bar{U}_1 \times \bar{U}_2$) such that for any $\bar{x} := (\bar{x}_1,\bar{x}_2,\bar{x}_3) \in \bar{X}$ and $\bar{u} := (\bar{u}_1,\bar{u}_2) \in \bar{U}$, one has $\bar{x}_1 \in \bar{X}_1$, $\bar{x}_2 \in \bar{X}_2$, $\bar{x}_3 \in \bar{X}_3$, $\bar{u}_1 \in \bar{U}_1$, and $\bar{u}_2 \in \bar{U}_2$. Now, based on the dependency graph, $P^f_1(\bar{x}) := \pi _{\bar{X}_1 \times \bar{X}_3}(\bar{x}) = (\bar{x}_1,\bar{x}_3)$ and $P^f_1(\bar{u}) := \pi _{\bar{U}_1 \times \bar{U}_2}(\bar{u}) = (\bar{u}_1,\bar{u}_2)$. We can also apply the map to subsets of $\bar{X}$ and $\bar{U}$, e.g., $P^f_1(\bar{X}) = \bar{X}_1 \times \bar{X}_3$, and $P^f_1(\bar{U}) = \bar{U}_1 \times \bar{U}_2$.

For a transition element $t = (\bar{x},\bar{u},\bar{x}') \in T$, we define $P^f_i(t) := (P^f_i(\bar{x}), P^f_i(\bar{u}), \pi _{\bar{X}_i}(\bar{x}'))$, for any component $i \in \{1,2,\cdots ,n\}$. Note that for t, the successor state $\bar{x}'$ is treated differently as it is related directly to the updated state variable $\bar{x}^+_i$. We can apply the map to subsets of T, e.g., for the given update-dependency graph in Fig. 1, one has $P^f_1(T) = \bar{X}_1 \times \bar{X}_3 \times \bar{U}_1 \times \bar{U}_2 \times \bar{X}_1$.

On the other hand, a generic recovery map

$$\begin{aligned} D^f_i : P^f_i(A) \rightarrow 2^A, \end{aligned}$$

is used to recover elements (resp. subsets) from the projected subsets back to their original monolithic sets. Similarly, $A \subseteq \bar{X} := \bar{X}_1 \times \bar{X}_2 \times \cdots \times \bar{X}_n$ when we are interested in subsets of the state set and $A \subseteq \bar{U} := \bar{U}_1 \times \bar{U}_2 \times \cdots \times \bar{U}_m$ when we are interested in subsets of the input set.

For the same example in Fig. 1, let $\bar{x} := (\bar{x}_1,\bar{x}_2,\bar{x}_3) \in \bar{X}$ be a state. Now, define $\bar{x}_p := P^f_1(\bar{x}) = (\bar{x}_1,\bar{x}_3)$. We then have $D^f_1(\bar{x}_p) := \{ (\bar{x}_1,\bar{x}^*_2,\bar{x}_3) \;\vert \; \bar{x}^*_2 \in \bar{X}_2 \}$. Similarly, for a transition element $t := ((\bar{x}_1,\bar{x}_2,\bar{x}_3),(\bar{u}_1,\bar{u}_2), (\bar{x}'_1,\bar{x}'_2,\bar{x}'_3)) \in T$ and its projection $t_p := P^f_1(t) = ((\bar{x}_1,\bar{x}_3),(\bar{u}_1,\bar{u}_2), (\bar{x}'_1))$, the recovered transitions is the set $D^f_1(t_p) = \{ ((\bar{x}_1,\bar{x}^*_2,\bar{x}_3),(\bar{u}_1,\bar{u}_2), (\bar{x}'_1,\bar{x}'^*_2,\bar{x}'^*_3)) \;\vert \; \bar{x}^*_2 \in \bar{X}_2 \text {, } \bar{x}'^*_2 \in \bar{X}_2 \text {, and } \bar{x}'^*_3 \in \bar{X}_3 \}$.

Given a subset $\widetilde{X} \subseteq \bar{X}$, let $[\widetilde{X}] := D^f_1 \circ P^f_1(\widetilde{X})$. Note that $[\widetilde{X}]$ is not necessarily equal to $\widetilde{X}$. However, we have that $\widetilde{X} \subseteq [\widetilde{X}]$. Here, $[\widetilde{X}]$ over-approximates $\widetilde{X}$.

For an update map f in (1), a function $\varOmega ^{f} : \bar{X} \times \bar{U} \rightarrow X \times X$ characterizes hyper-rectangles that over-approximate the reachable sets starting from a set $\bar{x} \in \bar{X}$ when the input $\bar{u}$ is applied. For example, if a growth bound map ($\beta :\mathbb {R}^n \times U \rightarrow \mathbb {R}^n$) is used, $\varOmega ^f$ can be defined as follows:

$$\begin{aligned} \varOmega ^f(\bar{x}, \bar{u}) = (x_{lb},x_{ub}) := (-r+f(\bar{x}_c,\bar{u}),r+f(\bar{x}_c,\bar{u})), \end{aligned}$$

where $r = \beta (\eta /2,u)$, and $\bar{x}_c \in \bar{x}$ denotes the centroid of $\bar{x}$. Here, $\beta$ is the growth bound introduced in [8, Section VIII]. An over-approximation of the reachable sets can then be obtained by the map $O^f : \bar{X} \times \bar{U} \rightarrow 2^{\bar{X}}$ defined by:

$$\begin{aligned} O^f(\bar{x}, \bar{u}) := Q\circ \varOmega ^f(\bar{x}, \bar{u}), \end{aligned}$$

where Q is a quantization map defined by:

$$\begin{aligned} Q(x_{lb},x_{ub}) = \{ \bar{x}' \in \bar{X} \;\vert \; \bar{x}' \cap [\![ x_{lb},x_{ub} ]\!] \ne \emptyset \}, \end{aligned}$$

(2)

where $[\![ x_{lb},x_{ub} ]\!] = [x_{lb,1},x_{ub,1}]\times [x_{lb,2},x_{ub,2}]\times \cdots \times [x_{lb,n},x_{ub,n}]$.

We also assume that $O^f$ can be decomposed component-wise (i.e., for each dimension $i \in \{1,2,\cdots ,n\}$) such that for any $(\bar{x},\bar{u}) \in \bar{X} \times \bar{U}$, $O^f(\bar{x},\bar{u}) = \bigcap _{i=1}^{n} D^f_i(O^f_i(P^f_i(\bar{x}),P^f_i(\bar{u})))$, where $O^f_i : P^f_i(\bar{X}) \times P^f_i(\bar{U}) \rightarrow 2^{P^f_i(\bar{X})}$ is an over-approximation function restricted to component $i \in \{1,2,\cdots ,n\}$ of f. The same assumption applies to the underlying characterization function $\varOmega ^f$.

3 Sparsity-Aware Distributed Constructions of Abstractions

Traditionally, constructing $\bar{\varSigma }$ is achieved monolithically and sequentially. This includes current state-of-the-art tools, e.g. SCOTS [9], PESSOA [6], CoSyMa [7], and SENSE [3]. More precisely, such tools have implementations that serially traverse each element $(\bar{x},\bar{u}) \in \bar{X} \times \bar{U}$ to compute a set of transitions $\{ (\bar{x},\bar{u},\bar{x}') \;\vert \; \bar{x}' \in O^f(\bar{x},\bar{u}) \}$. Algorithm 1 presents the traditional serial algorithm (denoted by SA) for constructing $\bar{\varSigma }$.

The drawback of this exhaustive search was mitigated by the technique introduced in [2] which utilizes the sparsity of $\bar{\varSigma }$. The authors suggest constructing T by applying Algorithm 1 to subsets of each component. Algorithm 2 presents a sparsity-aware serial algorithm (denoted by Sparse-SA) for constructing $\bar{\varSigma }$, as introduced in [2]. If we assume a bounded number of elements in subsets of each component (i.e., $\vert P^f_i(\bar{X}) \vert$ and $\vert P^f_i(\bar{U}) \vert$ from line 3 in Algorithm 2), we would expect a near-linear complexity of the algorithm. This is not clearly the case in [2, Figure 3] as the authors decided to use Binary Decision Diagrams (BDD) to represent transition relation T.

Clearly, representing T as a single storage entity is a drawback in Algorithm 2. All component-wise transition sets $T_i$ will eventually need to push their results into T. This hinders any attempt to parallelize it unless a lock-free data structure is used, which affects the performance dramatically.

On the other hand, Algorithm 2 in [4] introduces a technique for constructing $\bar{\varSigma }$ by using a distributed data container to maintain the transition set T without constructing it explicitly. In [4], using a continuous over-approximation $\varOmega ^f$ is favored as opposed to the discrete over-approximation $O^f$ since it requires less memory in practice. The actual computation of transitions (i.e., using $O^f$ to compute discrete successor states) is delayed to the synthesis phase and done on the fly. The parallel algorithm scales remarkably with respect to the number of PEs, denoted by P, since the task is parallelizable with no data dependency. However, it still handles the problem monolithically which means, for a fixed P, it will not probably scale as the system dimension n grows.

Fig. 2.

An example task distributions for the parallel sparsity-aware abstraction.

We then introduce Algorithm 3 which utilizes sparsity to construct $\bar{\varSigma }$ in parallel, and is a combination of Algorithm 2 in [4] and Algorithm 2. Function $I:\mathbb {N}_+\setminus \{\infty \} \times \mathbb {N}_+\setminus \{\infty \} \rightarrow \{1,2,\cdots ,P\}$ maps a parallel job (i.e., lines 9 and 10 inside the inner parallel for-all statement), for a component i and a tuple $(\bar{x},\bar{u})$ with index j, to a PE with an index $p = I(i,j)$. $K^p_{loc,i}$ stores the characterizations of abstraction of ith component and is located in PE of index p. Collectively, $K^1_{loc,1},$ $\, \ldots , K^p_{loc, i},$$\,\ldots , K^P_{loc, n}$ constitute a distributed container that stores the abstraction of the system.

Figure 2 depicts an example of the job and task distributions for the example presented in Fig. 1. Here, we use $P = 6$ with a mapping I that distributes one partition element of one subset $P^f_i(\bar{X}) \times P^f_i(\bar{U})$ to one PE. We also assume that the used PEs have equal computation power. Consequently, we try to divide each subset $P^f_i(\bar{X}) \times P^f_i(\bar{U})$ into two equal partition elements such that we have, in total, 6 similar computation spaces. Inside each partition element, we indicate which distributed storage container $K^p_{loc,i}$ is used.

Fig. 3.

Comparison between the serial and parallel algorithms for constructing abstractions of a traffic network model by varying the dimensions.

To assess the distributed algorithm in comparison with the serial one presented in [2], we implement it in pFaces. We use the same traffic model presented in [2, Subsection VI-B] and the same parameters. For this example, the authors of [2] construct $T_i$, for each component $i \in \{1,2,\cdots ,n\}$. They combine them incrementally in a BDD that represents T. A monolithic construction of T from $T_i$ is required in [2] since symbolic controllers synthesis is done monolithically. On the other hand, using $K^p_{loc,i}$ in our technique plays a major role in reducing the complexity of constructing higher dimensional abstractions. In Sect. 4, we utilize $K^p_{loc,i}$ directly to synthesize symbolic controllers with no need to explicitly construct T.

Figure 3 depicts a comparison between the results reported in [2, Figure 3] and the ones obtained from our implementation in pFaces. We use an Intel Core i5 CPU, which comes equipped with an internal GPU yielding around 24 PEs being utilized by pFaces. The implementation stores the distributed containers $K^p_{loc,i}$ as raw-data inside the memories of their corresponding PEs. As expected, the distributed algorithm scales linearly and we are able to go beyond 100 dimensions in a few seconds, whereas Figure 3 in [2] shows only abstractions up to a 51-dimensional traffic model because constructing the monolithic T begins to incur an exponential cost for higher dimensions.

Remark 1

Both Algorithms 2 and 3 utilize sparsity of $\varSigma$ to reduce the space complexity of abstractions from $\vert \bar{X} \times \bar{U} \vert$ to $\sum _{i=1}^{n} \vert P^f_i(\bar{X}) \times P^f_i(\bar{U}) \vert$. However, Algorithm 2 iterates over the space serially. Algorithm 3, on the other hand, handles the computation over the space in parallel using P PEs.

4 Sparsity-Aware Distributed Synthesis of Symbolic Controllers

Given an abstract system $\bar{\varSigma } = (\bar{X},\bar{U},T)$, we define the controllable predecessor map $CPre^{T} : 2^{\bar{X} \times \bar{U}} \rightarrow 2^{\bar{X} \times \bar{U}}$ for $Z \subseteq \bar{X} \times \bar{U}$ by:

$$\begin{aligned} CPre^{T}(Z) = \{ (\bar{x},\bar{u}) \in \bar{X} \times \bar{U} \;\vert \; \emptyset \ne T(\bar{x},\bar{u}) \subseteq \pi _{\bar{X}}(Z) \}, \end{aligned}$$

(3)

where $T(\bar{x},\bar{u})$ is an interpretation of the transitions set T as a map $T: \bar{X} \times \bar{U} \rightarrow 2^{\bar{X}}$ that evaluates a set of successor states from a state-input pair. Similarly, we introduce a component-wise controllable predecessor map $CPre^{T_i} : 2^{P^f_i(\bar{X}) \times P^f_i(\bar{U})} \rightarrow 2^{P^f_i(\bar{X}) \times P^f_i(\bar{U})}$, for any component $i \in \{1,2,\cdots ,n\}$ and any $\widetilde{Z} := P^f_i(Z) := \pi _{P^f_i(\bar{X}) \times P^f_i(\bar{U})}(Z)$, as follows:

$$\begin{aligned} CPre^{T_i}(\widetilde{Z}) = \{ (\bar{x},\bar{u}) \in P^f_i(\bar{X}) \times P^f_i(\bar{U}) \;\vert \; \emptyset \ne T_i(\bar{x},\bar{u}) \subseteq \pi _{\bar{X}_i}(\widetilde{Z}) \}. \end{aligned}$$

(4)

Proposition 1

The following inclusion holds for any $i \in \{1,2,\cdots ,n\}$ and any $Z \subseteq \bar{X} \times \bar{U}$:

$$\begin{aligned} P^f_i(CPre^T(Z)) \subseteq CPre^{T_i}(P^f_i(Z)). \end{aligned}$$

Proof

Consider an element $z_p \in P^f_i(CPre^T(Z))$. This implies that there exists $z \in \bar{X} \times \bar{U}$ such that $z \in CPre^T(Z)$ and $z_p = P^f_i(z)$. Consequently, $T_i(z_p) \ne \emptyset$ since $T(z) \ne \emptyset$. Also, since $z \in CPre^T(Z)$, then $T(z) \subseteq \pi _{\bar{X}}(Z)$. Now, recall how $T_i$ is constructed as a component-wise set of transitions in line 2 in Algorithm 2. Then, we conclude that $T_i(z_p) \subseteq \pi _{\bar{X}_i}(P^f_i(Z))$. By this, we already satisfy the requirements in (4) such that $z_p = (\bar{x},\bar{u}) \in CPre^{T_i}(Z)$.

Here, we consider reachability and invariance specifications given by the LTL formulae $\Diamond \psi$ and $\square \psi$, respectively, where $\psi$ is a propositional formula over a set of atomic propositions AP. We first construct an initial winning set $Z_\psi = \{ (\bar{x},\bar{u}) \in \bar{X}\times \bar{U} \;\vert \; L(\bar{x},\bar{u}) \models \psi ) \}$, where $L : \bar{X}\times \bar{U} \rightarrow 2^{AP}$ is some labeling function. During the rest of this section, we focus on reachability specifications for the sake of space and a similar discussion can be pursued for invariance specifications.

Traditionally, to synthesize symbolic controllers for the reachability specifications $\Diamond \psi$, a monotone function:

$$\begin{aligned} \underline{G}(Z) := CPre^{T}(Z) \cup Z_{\psi } \end{aligned}$$

(5)

is employed to iteratively compute $Z_{\infty } = \mu Z.\underline{G}(Z)$ starting with $Z_0 = \emptyset$. Here, a notation from $\mu$-calculus is used with $\mu$ as the minimal fixed point operator and Z $\subseteq \bar{X}\times \bar{U}$ is the operated variable representing the set of winning pairs $(\bar{x},\bar{u}) \in \bar{X}\times \bar{U}$. Set $Z_{\infty } \subseteq \bar{X}\times \bar{U}$ represents the set of final winning pairs, after a finite number of iterations. Interested readers can find more details in [5] and the references therein. The transition map T is used in this fixed-point computation and, hence, the technique suffers directly from the state-explosion problem. Algorithm 4 depicts a traditional serial algorithm of symbolic controller synthesis for reachability specifications. The synthesized controller is a map $\underline{C} : \bar{X}_w \rightarrow 2^{\bar{U}}$, where $\bar{X}_w \subseteq \bar{X}$ represents a winning (a.k.a. controllable) set of states. Map $\underline{C}$ is defined as: $\underline{C}(\bar{x}) = \{\bar{u} \in \bar{U} \;\vert \; (\bar{x}, \bar{u}) \in \mu ^{j(\bar{x})} Z.\underline{G}(Z) \}$, where $j(\bar{x}) = \inf \{i \in \mathbb {N}\;\vert \; \bar{x} \in \pi _{\bar{X}}(\mu ^{i} Z.\underline{G}(Z))\}$, and $\mu ^{i} Z.\underline{G}(Z)$ represents the set of state-input pairs by the end of the ith iteration of the minimal fixed point computation.

A parallel implementation that mitigates the complexity of the fixed-point computation is introduced in [4, Algorithm 4]. Briefly, for a set $Z \subseteq \bar{X} \times \bar{U}$, each iteration of $\mu Z.\underline{G}(Z)$ is computed via parallel traversal in the complete space $\bar{X} \times \bar{U}$. Each PE is assigned a disjoint set of state-input pairs from $\bar{X} \times \bar{U}$ and it declares whether, or not, each pair belongs to the next winning pairs (i.e., $\underline{G}(Z)$). Although the algorithm scales well w.r.t P, it still suffers from the state-explosion problem for a fixed P. We present a modified algorithm that utilizes sparsity to reduce the parallel search space at each iteration.

First, we introduce the component-wise monotone function:

$$\begin{aligned} \underline{G}_i(Z) := CPre^{T_i}(P^f_i(Z)) \cup P^f_i(Z_{\psi }), \end{aligned}$$

(6)

for any $i \in \{1,2,\cdots ,n\}$ and any $Z \in \bar{X} \times \bar{U}$. Now, an iteration in the sparsity-aware fixed-point can be summarized by the following three steps:

• (1) Compute the component-wise sets $\underline{G}_i(Z)$. Note that $\underline{G}_i(Z)$ lives in the set $P^f_i(\bar{X}) \times P^f_i(\bar{U})$.

• (2) Recover a monolithic set $\underline{G}_i(Z)$, for each $i \in \{1,2,\cdots ,n\}$, using the map $D^f_i$ and intersect these sets. Formally, we denote this intersection by:

  $$\begin{aligned}{}[\underline{G}(Z)] := \bigcap _{i=1}^{n}(D^f_i(\underline{G}_i(Z))). \end{aligned}$$

  (7)

  Note that $[\underline{G}(Z)]$ is an over-approximation of the monolithic set $\underline{G}(Z)$, which we prove in Theorem 1.

• (3) Now, based on the next theorem, there is no need for a parallel search in $\bar{X} \times \bar{U}$ and the search can be done in $[\underline{G}(Z)]$. More accurately, the search for new elements in the next winning set can be done in $[\underline{G}(Z)] \setminus Z$.

Theorem 1

Consider an abstract system $\bar{\varSigma } = (\bar{X}, \bar{U}, T)$. For any set $Z \in \bar{X} \times \bar{U}$, $\underline{G}(Z) \subseteq [\underline{G}(Z)]$.

Proof

Consider any element $z \in \underline{G}(Z)$. This implies that $z \in Z$, $z \in Z_\psi$ or $z \in CPre^T(Z)$. We show that $z \in [\underline{G}(Z)]$ for any of these cases.

• Case 1 [$z \in Z$]: By the definition of map $P^f_i$, we know that $P^f_i(z) \in P^f_i(Z)$. By the monotonicity of map $\underline{G}_i$, $P^f_i(Z) \subseteq \underline{G}_i(Z)$. This implies that $P^f_i(z) \in \underline{G}_i(Z)$. Also, by the definition of map $D^f_i$, we know that $z \in D^f_i(\underline{G}_i(Z))$. The above argument holds for any component $i \in \{1,2,\cdots ,n\}$ which implies that $z \in \bigcap _{i=1}^{n}(D^f_i(\underline{G}_i(Z))) = [\underline{G}(Z)]$.

• Case 2 [$z \in Z_\psi$]: The same argument used for the previous case can be used for this one as well.

• Case 3 [$z \in CPre^T(Z)$]: We apply the map $P^f_i$ to both sides of the inclusion. We then have $P^f_i(z) \in P^f_i(CPre^T(Z))$. Using Proposition 1, we know that $P^f_i(CPre^T(Z)) \subseteq CPre^{T_i}(Z)$. This implies that $P^f_i(z) \in CPre^{T_i}(P^f_i(Z))$. From (6) we obtain that $P^f_i(z) \in \underline{G}_i(Z)$, and consequently, $z \in D^f_i(\underline{G}_i(Z))$. The above argument holds for any component $i \in \{1,2,\cdots ,n\}$. This, consequently, implies that $z \in \bigcap _{i=1}^{n}(D^f_i(\underline{G}_i(Z))) = [\underline{G}(Z)]$, which completes the proof.

Remark 2

An initial computation of the controllable predecessor is done component-wise in step (1) which utilizes the sparsity of $\bar{\varSigma }$ and can be easily implemented in parallel. Only in step (3) a monolithic search is required. However, unlike the implementation in [4, Algorithm 4], the search is performed only for a subset of $\bar{X} \times \bar{U}$, which is $[\underline{G}(Z)] \setminus Z$.

Note that dynamical systems pose some locality property (i.e., starting from nearby states, successor states are also nearby) and an initial winning set will grow incrementally with each fixed-point iteration. This makes the set $[\underline{G}(Z)] \setminus Z$ relatively small w.r.t $\vert \bar{X} \times \bar{U} \vert$. We clarify this and the result in Theorem 1 with a small example.

4.1 An Illustrative Example

For the sake of illustrating the proposed sparsity-aware synthesis technique, we provide a simple two-dimensional example. Consider a robot described by the following difference equation:

$$\begin{aligned} \begin{bmatrix} x^+_1\\ x^+_2\\ \end{bmatrix} = \begin{bmatrix} x_1 + \tau u_1\\ x_2 + \tau u_2\\ \end{bmatrix}, \end{aligned}$$

Fig. 4.

A visualization of one arbitrary fixed-point iteration of the sparsity-aware synthesis technique for a two-dimensional robot system.

Fig. 5.

The evolution of the fixed-point sets for the robot example by the end of fixed-point iterations 5 (left side) and 228 (right side). A video of all iterations can be found in: http://goo.gl/aegznf.

where $(x_1, x_2) \in \bar{X} := \bar{X}_1 \times \bar{X}_2$ is a state vector and $(u_1, u_2) \in \bar{U} := \bar{U}_1 \times \bar{U}_2$ is an input vector. Figure 4 shows a visualization of the sets related to this sparsity-aware technique for symbolic controller synthesis for one fixed-point iteration. Set $Z_\psi$ is the initial winning-set (a.k.a. target-set for reachability specifications) constructed from a given specification (e.g., a region in $\bar{X}$ to be reached by the robot) and Z is the winning-set of the current fixed-point iteration. For simplicity, all sets are projected on $\bar{X}$ and the readers can think of $\bar{U}$ as an additional dimension perpendicular to the surface of this paper.

As depicted in Fig. 4, the next winning-set $\underline{G}(Z)$ is over-approximated by $[\underline{G}(Z)]$, as a result of Theorem 1. Algorithm 4 in [4] searches for $\underline{G}(Z)$ in $(\bar{X}_1 \times \bar{X}_2) \times (\bar{U}_1 \times \bar{U}_2)$. This work suggests searching for $\underline{G}(Z)$ in $[\underline{G}(Z)] \setminus Z$ instead.

4.2 A Sparsity-Aware Parallel Algorithm for Symbolic Controller Synthesis

We propose Algorithm 5 to parallelize sparsity-aware controller synthesis. The main difference between this and Algorithm 4 in [4] are lines 9–12. They correspond to computing $[\underline{G}(Z)]$ at each iteration of the fixed-point computation. Line 13 is modified to do the parallel search inside $[\underline{G}(Z)] \setminus Z$ instead of $\bar{X} \times \bar{U}$ in the original algorithm. The rest of the algorithm is well documented in [4].

The algorithm is implemented in pFaces as updated versions of the kernels GBFP and $\mathtt{GBFP}_{\texttt {m}}$ in [4]. We synthesize a reachability controller for the robot example presented earlier. Figure 5 shows an arena with obstacles depicted as red boxes. It depicts the result at the fixed point iterations 5 and 228. The blue box indicates the target set (i.e., $Z_\psi$). The region colored with purple indicates the current winning states. The orange region indicates $[\underline{G}(Z)] \setminus Z$. The black box is the next search region which is a rectangular over approximation of the $[\underline{G}(Z)] \setminus Z$. We over-approximate $[\underline{G}(Z)] \setminus Z$ with such rectangle as it is straightforward for PEs in pFaces to work with rectangular parallel jobs. The synthesis problem is solved in 322 fixed-point iterations. Unlike the parallel algorithm in [4] which searches for the next winning region inside $\bar{X} \times \bar{U}$ at each iteration, the implementation of the proposed algorithm reduces the parallel search by an average of 87% when searching inside the black boxes in each iteration.

Fig. 6.

An autonomous vehicle trying to avoid a sudden obstacle on the highway.

5 Case Study: Autonomous Vehicle

We consider a vehicle described by the following 7-dimensional discrete-time single track (ST) model [1]:

$$\begin{aligned} \begin{array}{rcl} x^+_1 &{} = &{} x_1 + \tau x_4 \cos (x_5 + x_7), \\ x^+_2 &{} = &{} x_2 + \tau x_4 \sin (x_5 + x_7), \\ x^+_3 &{} = &{} x_3 + \tau u_1, \\ x^+_4 &{} = &{} x_4 + \tau u_2, \\ x^+_5 &{} = &{} x_5 + \tau x_6, \\ x^+_6 &{} = &{} x_6 + \frac{\tau \mu m}{I_z (l_r + l_f)} \big (l_f C_{S,f} (g l_r - u_2 h_{cg}) x_3 + (l_r C_{S,r} (g l_f + u_2 h_{cg}) - l_f C_{S,f} (g l_r \\ &{} &{} \;\;\;\;\;\;\;\; - u_2 h_{cg})) x_7 - (l_f l_f C_{S, f} (g l_r - u_2 h_{cg}) + l_r^2 C_{S,r} (g l_f + u_2 h_{cg})) \frac{x_6}{x_4} \big ),\\ x^+_7 &{} = &{} x_7 + \frac{\tau \mu }{x4*(lf+lr)} \big (C_{S,f} (g l_r - u_2 h_{cg}) x_3 - (C_{S,r} (g l_f + u_2 h_{cg}) + C_{S,f} (g l_r \\ &{} &{} \;\;\;\;\;\;\;\; - u_2 h_{cg})) x_7 + (C_{s,r} (g l_f + u_2 h_{cg}) l_r - C_{S,f} (g l_r - u_2 h_c{g}) l_f)\frac{x_6}{x_4} \big )-x_6, \end{array} \end{aligned}$$

where $x_1$ and $x_2$ are the position coordinates, $x_3$ is the steering angle, $x_4$ is the heading velocity, $x_5$ is the yaw angle, $x_6$ is the yaw rate, and $x_7$ is the slip angle. Variables $u_1$ and $u_2$ are inputs and they control the steering angle and heading velocity, respectively. Input and state variables are all members of $\mathbb {R}$. The model takes into account tire slip making it a good candidate for studies that consider planning of evasive maneuvers that are very close to the physical limits. We consider an update period $\tau = 0.1$ s and the following parameters for a BMW 320i car: $m = 1093$ [kg] as the total mass of the vehicle, $\mu = 1.048$ as the friction coefficient, $l_f = 1.156$ [m] as the distance from the front axle to center of gravity (CoG), $l_r = 1.422$ [m] as the distance from the rear axle to CoG, $h_{cg} = 0.574$ [m] as the height of CoG, $I_z = 1791.0$ [kg m$^2$] as the moment of inertia for entire mass around z axis, $C_{S,f} = 20.89$ [1/rad] as the front cornering stiffness coefficient, and $C_{S,r} = 19.89$ [1/rad] as the rear cornering stiffness coefficient.

To construct an abstract system $\bar{\varSigma }$, we consider a bounded version of the state set $X := [0,84] \times [0,6] \times [-0.18,0.8] \times [12,21] \times [-0.5,0.5] \times [-0.8,0.8] \times [-0.1,0.1]$, a state quantization vector $\eta _X = (1.0, 1.0, 0.01, 3.0, 0.05, 0.1, 0.02)$, a input set $U := [-0.4,0.4] \times [-4,4]$, and an input quantization vector $\eta _U = (0.1, 0.5)$.

Table 1. Used HW configurations for testing the proposed technique.

We are interested in an autonomous operation of the vehicle on a highway. Consider a situation on two-lane highway when an accident happens suddenly on the same lane on which our vehicle is traveling. The vehicle’s controller should find a safe maneuver to avoid the crash with the next-appearing obstacle. Figure 6 depicts such a situation. We over-approximate the obstacle with the hyper-box $[28,50] \times [0,3] \times [-0.18,0.8] \times [12,21] \times [-0.5,0.5] \times [-0.8,0.8] \times [-0.1,0.1]$.

Table 2. Results obtained after running the experiments EX$_1$ and EX$_2$.

We run the implementation on different HW configurations. We use a local machine and instances from Amazon Web Services (AWS) cloud computing services. Table 1 summarizes those configurations. We also run two different experiments. For the first one (denoted by EX$_1$), the goal is to only avoid the crash with the obstacle. We use a smaller version of the original state set $X := [0,50] \times [0,6] \times [-0.18,0.8] \times [11,19] \times [-0.5,0.5] \times [-0.8,0.8] \times [-0.1,0.1]$. The second one (denoted by EX$_2$) targets the full-sized highway window (84 m), and the goal is to avoid colliding with the obstacle and get back to the right lane. Table 2 reports the obtained results. The reported times are for constructing finite abstractions of the vehicle and synthesizing symbolic controllers. Note that our results outperform easily the initial kernels in pFaces which itself outperforms serial implementations with speedups up to 30000x as reported in [4]. The speedup in EX$_1$ is higher as the obstacle consumes a relatively bigger volume in the state space. This makes $[\underline{G}(Z)] \setminus Z$ smaller and, hence, faster for our implementation.

6 Conclusion and Future Work

A unified approach that utilizes sparsity of the interconnection structure in dynamical systems is introduced for the construction of finite abstractions and synthesis of their symbolic controllers. In addition, parallel algorithms are designed to target HPC platforms and they are implemented within the framework of pFaces. The results show remarkable reductions in computation times. We showed the effectiveness of the results on a 7-dimensional model of a BMW 320i car by designing a controller to keep the car in the travel lane unless it is blocked.

The technique still suffers from the memory inefficiency as inherited from pFaces. More specifically, the data used during the computation of abstraction and the synthesis of symbolic controllers is not encoded. Using raw data requires larger amounts of memory. Future work will focus on designing distributed data-structures that achieve a balance between memory size and access time.