Abstract
The present report is based on the National Forest Soil Inventory (NFSI) as well as on case studies from Intensive Forest Monitoring sites in Germany. The current as well as the temporal development of forest soil conditions and the major threats to forest ecosystems are discussed. Following the discussion on forest decline in 1980s, a national forest monitoring was established, consisting of the Forest Condition Survey, the Intensive Forest Monitoring as well as the NFSI. In 1984, the sites for the Forest Condition Survey were installed on a 16 × 16 km grid which is part of the UN/ECE ICP Forests Level I Monitoring as well as of the European Soil Monitoring Project (BioSoil). The NFSI plots were subsequently established based on the same grid with an 8 × 8 km raster yielding at about 1800 sampling sites. The first NFSI took place between 1987 and 1992. In 2006, the second NFSI was conducted simultaneously with the BioSoil programme. The NFSI focused on specific questions for forest soils in respect to nitrogen levels and sensitivity to inputs of nitrogen; to carbon storage and carbon stock changes; to background loading with heavy metals and organic trace elements; to the interplay of soil characteristics and forest nutrition, crown condition and vegetation; to the risk due to negative changes such as nutrient removal or soil acidification; and to effects in terms of soil chemistry and nutritional status measures to stabilize forest ecosystems. To fulfil these objectives, the NFSI included the sampling of chemical and physical soil parameters, the determination of foliar element concentrations, the assessment of the composition and diversity of understory vegetation as well as an inventory of the tree stands including dead wood. A comprehensive concept of quality control and quality assurance for field assessments, laboratories, data management and evaluations has been established to ensure data harmonization and a high quality of statistical evaluations.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1.1 Introduction
What is the state of our forests and forest soils today? How have they changed over the past 20 years? What actions have had an effect on their status and how? What are the risks that continue to play a role or become relevant in the future? The present report based on the National Forest Soils Inventory (NFSI) as well as on case studies from Intensive Forest Monitoring sites in Germany (see below) addresses these questions and provides a nationwide summary on the current state and development of forests and forest soils. The results offer scientific evidence supporting the evaluation of forest management approaches and policy options at different spatial scales.
Forest soils are the basis for productive and resilient forests that in turn create opportunities for sustainable and successful forest management. Soils provide water and nutrients required for forest growth, buffer loading of toxins and acidification and compensate for water shortages during droughts. Forests and their soils represent one of Germany’s most natural ecosystems and contribute an important share to its biodiversity. As carbon (C) sinks (Höhle et al. 2018), forests and their soils play a key role in climate protection and compensating for greenhouse gas emissions (Leitgeb et al. 2013).
The current condition of forest soils is the result of both natural changes over long periods of time and anthropogenic influences. Natural factors that contribute to the formation of soils include the parent material , climate, relief and the flora and fauna (Blume et al. 2010).
Over the past decades, impacts from atmospheric pollution caused by humans have had a significant impact on forests (Ellenberg 1971; Ulrich 1987). At the end of the 1970s and in the early 1980s, air pollution effects on forests became evident based on the condition of the crowns of the trees, followed by the discussion about “forest dieback” and new types of forest damage (Kauppi et al. 1990; Ulrich 1983). In addition, for many German forest stands, an increasing risk of drought stress has been identified over the last 60 years, due to climate change (von Wilpert et al. 2016; Schmidt-Walter et al. 2017). Thus, forests can suffer also from interactive effects of both atmospheric pollution and climate change impacts like increasing drought (Bytnerowicz et al. 2007; Hickler et al. 2012).
1.2 The National Forest Soils Inventory as a Part of the Forest Monitoring in Germany
Following the discussion on forest decline , a national forest monitoring was established, consisting of the periodic assessment of crown condition , the establishment of selected Intensive Forest Monitoring sites as well as the nationwide crown and soil condition inventory (National Forest Soils Inventory; NFSI). In 1984, the crown condition plots were established on a 16 × 16 km grid . The 8 × 8 km grid of NFSI plots was subsequently installed based on the same grid. As a consequence, every fourth NFSI plot is one of the original crown condition plots that became part of the European Level I net of the UN/ECE “International Co-operative Programme on Assessment and Monitoring of Air Pollution Effects on Forests” (ICP Forests) and were also part of the EU BioSoil project. In 2006, a soil inventory took place on these plots. All data had been submitted to the Joint Research Centre (JRC) of the european commission.
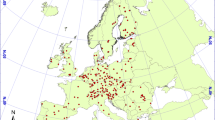
The NFSI was launched at the end of the 1980s/beginning of the 1990s with surveys taking place at approximately 1900 sampling sites (Fig. 1.1). While the data gathered in this survey are an important pool of information on its own, integrated evaluations, for example, with data from the Intensive Forest Monitoring programme (Level II ), allow for comprehensive interpretation of the NFSI data. The Level II programme was initiated by the UN/ECE under the “International Co-operative Programme on Assessment and Monitoring of Air Pollution Effects on Forests” (ICP Forests), too. Most German sites were established during the mid-1990s by the federal states, and many of them have been active since then, partly co-funded by the EU. In 2014, a German legislation secured the long-term operation of 68 Level II sites (Fig. 1.1). The case studies of the Level II programme aim at understanding cause-effect relationships in forest ecosystems, based on measurements of a comprehensive set of parameters. For example, continuous assessments of deposition, growth and seepage water allow quantifying input-output element budgets.
In line with the federal structure of Germany, data collection for the NFSI plots and Level II sites is organized on the level of federal states. The data are compiled at the Thünen Institute for Forest Ecosystems for evaluations and assessments on a nationwide level. Data analysis took place in a collaborative effort involving the Thünen Institute, representatives of state forestry research institutes or environmental agencies and external experts. Special focus analyses on heavy metals and organic pollutants were conducted by the Federal Institute for Geosciences and Natural Resources (BGR) and the Federal Environmental Agency (UBA), respectively (Table 1.1).
1.3 Legal Framework
The second NFSI was initiated in 2001 in a resolution at the Forest Executive Conference (Forstchefkonferenz; FCK). Data and analyses from the NFSI provide an important basis for the national reporting on greenhouse gases under the Framework Convention on Climate Change (UNFCCC) and the Kyoto Protocol , as well as succeeding regulations in the “land use , land-use change and forestry” (LULUCF) soil group in the areas of soil and litter. The NFSI provides information useful in implementing the Federal Soil Protection Act (Bundes-Bodenschutzgesetz) in particular §9 which averting the risk of harmful soil contaminations. An important link to international forest monitoring is presented within the framework of the UNECE Convention on Long-range Transboundary Air Pollution (also known as the Air Convention; CLRTAP). The NFSI data represent an essential part of Germany’s national contribution to the “International Co-operative Programme on Assessment and Monitoring of Air Pollution Effects on Forests” (ICP Forests) as a CLRTAP programme specific to forests. These commitments to national and international policy advice and monitoring programmes require periodic updates on the condition of forest soils. A step towards a legal basis for this effort has been done by the 2010 amendment to §41a of the Federal Forest Act. It allows the Federal Ministry for Food and Agriculture (BMEL) to collect data on the supply of nutrients and pollution loading in forest soils through legislative decree with the approval of the states. However, corresponding legislation for the third NFSI will be tabled in 2019.
1.4 Objectives and Key Questions
The goal of the NFSI is to generate reliable data on the current state and changes in forest soils and selected features of the forests based on a systematic 8 × 8 km grid and a repetition of the inventory every 15 years. The information collected is representative on regional scale and comparable across the country. Analysis of the status and temporal changes is differentiated by region, allowing for the identification of areas of particular risk. The comparison with previous surveys, especially the NFSI I, is used to identify changes over time. The national grid of the NFSI sites can be also used to regionalize processes and findings that have been identified on the smaller scale of the Intensive Forest Monitoring (Level II programme). The NFSI therefore allows for estimating risks like soil acidification or eutrophication of forest stands. Furthermore, the effects of large-scale soil treatments, such as liming , can be analysed based on NFSI results. As such, the NFSI is able to contribute to planning of sustainable forest management , including balanced soil C and nutrient budgets. Besides providing advice for practical forest management approaches, the NFSI results offer scientific evidence supporting the assessment of higher-level forest and environmental measures and strategies.
The report consists of (I) a text volume presenting the methods and findings as well as (II) a map volume containing point analyses, composite curves and statistical parameters. Specifically, the study addresses questions in the following areas:
-
Soil acidification
-
Nitrogen status and dynamics in forest soils and soil sensitivity to ongoing inputs of nitrogen
-
Current carbon storage and changes of carbon stocks in forest soils (Framework Convention on Climate Change and the Kyoto Protocol )
-
Background loading of soils with heavy metals and organic trace elements
-
The interplay of soil characteristics and forest nutrition , crown condition and vegetation
-
Risks due to negative changes such as nutrient removal or soil acidification in relation to nature conservation and sustainable use of forests
-
Effects in terms of soil chemistry and nutritional status on measures to stabilize forest ecosystems (efficiency monitoring, in particular for soil liming and seminatural silviculture practices)
-
The extent of change of soil and forest conditions and the need for a subsequent inventory
1.5 Survey Parameters and Data Harmonization
The guidelines for the Second National Forest Soils Inventory were developed by the NFSI II federal-state working group (Wellbrock et al. 2006). The guidelines were designed to create a comprehensive working document for the field surveys for the NFSI II. Building on the guidelines for the First Soil Inventory in Forests (BMELF 1994), adjustments and enhancements were introduced based on new knowledge and requirements. As much as possible, these changes took into account the conventions of the NFSI I. The compatibility of the methods and their harmonization are presented in a separate volume (Höhle et al. 2018). The guidelines for the survey were supplemented with the “Handbuch Forstliche Analytik” (“Handbook of Forest Analysis”; HFA) prepared by the Forest Analysis Advisory Committee (GAFA) of the Federal Ministry for Food and Agriculture (BMEL), which describes the harmonized methodologies for laboratory analyses (GAFA 2005, 2009, 2014).
As specified by the federal-state working group, the NFSI II comprises the following focal areas (Wellbrock et al. 2006):
-
General description of the survey sites: point data, georeferencing, data on the environmental situation, forest inventory and data on factors causing changes to the soil
-
Soils: profile description, soil chemistry (including heavy metals and organic compounds) and soil physics separated according to mineral soil and organic layer
-
Sampling of needles or leaves
-
Collection of forest growth data (additional inventories modified after Hilbrig et al. 2014)
-
Crown condition
-
Ground vegetation
1.6 Inventory Design
The NFSI was conducted as a systematic sampling inventory of the condition of forest soils at a nationwide grid of 8 × 8 km, yielding at about 1900 soil sampling sites. The first survey took place from 1987 to 1992 (1991–1992 in the youngest federal states of Germany), and resampling was done from 2006 to 2008. As far as additional findings from the intensive forest monitoring programme are integrated, they refer to the current network of 68 “Level II ” sites (Fig. 1.1) and sometimes to additional plots sampled according to the same methodology.
1.7 Soil Sampling
1.7.1 National Forest Soils Inventory
The evaluation of the soil condition of the NFSI I was carried out according to an issued soil survey manual from (BMELF 1994). The standard methods for sampling soils at the NFSI grid plots involved sampling at eight satellites, with a soil profile at the centre of a plot (Fig. 1.2). Volume-based samples taken at the satellites were mixed for every depth level and plot. Satellites were distributed to main and minor geographic directions with a 10 m distance from the profile centre. Soil sampling plots of the NFSI II were shifted about 10 Gon from NFSI I satellites.
Sampling design of NFSI (Höhle et al. 2018, modified)
Soil profiles at the centre of the plot were used to designate soil horizons and classify soil types according to the manual of soil mapping (GAFA 2005, 2009, 2014). For both inventories, the forest floor litter with the fraction <20 mm was classified as organic layer. In general, the forest floor was divided into a litter (L), a moderately decomposed (Of) and a highly decomposed (Oh) layer if the layer thickness was >1 cm. At about 80% of the NFSI II plots, also the fraction >20 mm was sampled as forest floor material. The sampling of the forest floor was carried out by mixed samples at satellites with metal frames of different sizes. Different organic layers were accounted for as one layer and measured in thickness. Sampling of the mineral soil was obligatory for both inventories at satellites for the depth layers 0–5 cm, 5–10 cm, 10–30 cm, 30–60 cm and 60–90 cm either as mixed samples from the satellites or from the profile. Depending on stone concentration, volume-based mineral soil samples were taken with cylindrical core or cap cutter, with an AMS core sampler or a motor-driven auger.
1.7.2 Level II
The analysis of soil at individual German Intensive Forest Monitoring (Level II ) sites is conducted every 10 years. There is no fixed year of sampling that applies to all sites. The sampling site design as well as the sampling procedures , chemical analysis and quality checks are documented in the ICP Forests Manual (http://icp-forests.net/page/icp-forests-manual). Accordingly, soil samples are taken at a minimum of 24 locations within the plot, which are aggregated to at least 3 composite samples per site.
On most plots, the organic layer was divided into a litter (L), a moderately decomposed (Of) and a highly decomposed (Oh) layer and the mineral soil is sampled at fixed depths of 0–10 cm, 10–20 cm, 20–40 cm and 40–80 cm. The top 10 cm of the mineral soil shall be further divided into the layers 0–5 cm and 5–10 cm. Other methodological aspects of the Level II soil sampling are directly comparable to the methods described for the German NFSI.
1.8 Laboratory Analytics Quality Management
For the preparation of NFSI II, the Assessment Committee Forestry Analytical Methods (Gutachterausschuss Forstliche Analytik, GAFA) was formed by the Federal Ministry of Food and Agriculture to standardize, determine and document methods of analysis on the one hand and to develop and determine a quality control programme on the other. All analytical methods used by the NFSI I and NFSI II as well as by the German and international forest monitoring programmes like UN/ECE ICP Forests programme, EU BioSoil ), DIN and ISO Standards as well as the methods of the German federal states were subsequently documented and first published in 2005 by GAFA (GAFA 2005) in its manual on forestry analytics, the Handbuch forstliche Analytik (HFA). The HFA has been variously supplemented and is now available in the latest edition of 2014 (GAFA 2014).
The quality control programme encompassed 5 concomitant ring tests (3 soil and 2 humus tests of 6 samples each) and the entrainment of standard material for every survey parameter, which had to be analysed by every laboratory on at least 20 samples. Large quantities of six standard materials were produced for this purpose, and it was determined which material was to be analysed for which parameter. The evaluation of the ring tests (Blum and Heinbach 2010) and the examination of the standard materials showed that, barring few exceptions, the analytical data of the federal states and the laboratories can be evaluated comparatively (König et al. 2013). Only in 12 individual cases (laboratories of some federal states—a few parameters) the data for particular parameters of a laboratory or a federal state diverge in a directional bias from the data of the other institutions. The divergent data concerns in each case one laboratory/state of the parameter N (soil), Al, Ca , Fe , Mn and Zn in aqua regia digestion (humus), K in aqua regia digestion (soil), K and Na from the exchange capacity determination (humus) as well as pH (H20) and pH (KCl) (humus). For details see König et al. (2013). A real problem are the K concentrations in aqua regia digestion (soil and humus), because some laboratories have large directionally biased deviations, in one case so much that the data are not comparable to the other laboratories. This is probably caused by the different degrees to which samples are ground (Houba et al. 1993). Concerning all other parameters and analytical methods, it is safe to assume that the NFSI II data of all laboratories/states can be assessed together.
Based on the results, it must be assumed that the variation within as well as between the laboratories amounts to about 10%. Only few parameters show a slightly smaller variation [e.g. elemental analysis (soil) C, aqua regia digestion (soil) Ca and total digestion (soil) (Ca)]. Table 1.2 gives a general view of the average variations of standard analyses and the ring tests summarized for the particular methods of analysis and which parameters vary more markedly within the particular analytical methods.
1.9 Sample Preparation Methods
The sample preparation , analysis and element determination methods used in NFSI I and NFSI II partly differ due to methodological improvements. Apart from this, some laboratories/federal states have made their own methodological modifications or have even used entirely different methods as recommended/instructed. The report on documentation and harmonization of the National Forest Inventory (Höhle et al. 2018) lists in detail which parameters were used and which methods applied, as well as which differing methods were used in some federal states regarding NFSI I or NFSI II. The report also shows how, using available comparative methodology, it was checked to find out which methods were comparable and with which methods it was possible to convert the data using correlation analysis. In the following, therefore, only the standard methods used will be described, with reference to the exhaustive description in the manual Handbuch forstliche Analytik (HFA).
Prior to analysis all soil, humus or plant samples were, as a rule, stored at 4 °C (HFA, method A1.1.1). Humus or plant samples were dried at 60 °C (HFA A1.2.1 and B1.2.1) and soil samples at 40 °C (HFA A1.2.1). The soil samples were sieved by hand or by machine through a 2 mm mesh (HFA A1.3.1). Humus samples were also sieved or ground manually through a 2 mm mesh. However, in NFSI I the residue was discarded (HFA A1.3.1), whereas in NFSI II only the residue larger than 20 mm was discarded, while the particles between 2 and 20 mm were ground to size with suitable machinery and then added to the 2 mm fraction (HA A1.3.2). The admixture of the 2–20 mm fraction, a fraction with high timber content, to the <2 mm fraction results in lower nutrient or heavy metal content but in higher C levels. This effect is most pronounced in the L horizon of the humus layer, because there the 2–20 mm fraction predominates weight by weight over that in the Of and Oh horizon . A calculation of supply extenuates dilution and accumulation effects (<10%), because humus supply in the L horizon is lower in comparison with that of the Of and Oh horizon (Höhle et al. 2018). For this reason the supply rather than the concentration was compared between NFSI I and NFSI II, and the evaluation extended over the whole organic layer, and not so much with regard to individual layers.
Humus and soil samples were milled to a suitable gradation using ball or disc mills (HFA A1.4.1). For NFSI II humus samples of the 2–20 mm and <2 mm fractions were milled together. Plant samples were milled analytically fine (0.25 mesh) using ball or centrifugal mills (HFA B1.3.1).
1.10 Soil Physical Parameters
In soil layers down to 30 cm, the determination of the volumetric proportion of coarse fragments >2 mm (subscript “cf”, HFA A2,8) and of bulk density of fine earth was based on fixed volume samples taken with a cylinder (100 cm3) or equivalent devices. Coarse fragments were in most cases weighed and their volume calculated based on density of the minerals (D cf, mostly 2.65 g cm−3); alternatively their volume was measured. In soil layers below 30 cm with their usually higher proportion of coarse fragments, it was also accepted to use estimated volumetric proportions of coarse fragments from the soil profile (V%cf>20 mm) based on visually estimated and subsequently converted area proportions. Estimated values from NFSI I for layers above 30 cm were discarded in the evaluation process and replaced with the measurements from NFSI II.
Bulk density of fine earth (subscript “fe”) was measured depending on the volumetric proportion of coarse fragments: If it was below 5%, the fixed volume sample was completely dried at 105 °C and weighed such that bulk density (m/V, mass/volume) of the whole sample was taken as bulk density of fine earth.
Fixed volume samples with higher proportions of only smaller coarse fragments (2–20 mm) were sieved (2 mm including washing of remainder) in order to separate coarse fragments before determination of weight of fine earth. Bulk density of fine earth (BDfe, g cm−3) and fine earth stock (stockfe, t ha−1) were then calculated as:
In case of any proportion of larger coarse fragments (20–63 mm), they were visually estimated at the soil profile or by samples taken with a spade (Höhle et al. 2018). In that case, fine earth stock was calculated as:
Bulk density estimates from NFSI I based on penetration resistance were considered too rough estimates (Wirth et al. 2004) and not accepted in the evaluation process, but replaced by measurements or estimations from NFSI II. In case of yet available older bulk density measurements according to the described methodology, the sampling was not repeated in NFSI II (see Sect. 1.17.3).
1.11 Chemical Analysis of Soil and Humus
In order to determine the pH values of the NFSI I samples, these were mixed at a ratio of 1:2.5 (weight for mineral soil, volume for humus layer) with H2O (pH(H2O) ; HFA A3.1.1.1) or 1 M KCl solution (pH(KCl) ; HFA A3.1.1.3), and the pH value was determined with a glass electrode. For NFSI II the samples were mixed with a volume ratio sample: solution of 1:5 with H2O (pH(H2O); HFA A3.1.1.2), 1 M KCl solution (pH(KCl) ; HFA A3.1.1.4) or 0.01 M CaC12 solution (pH(CaCl2); HFA A3.1.1.7), and the pH value was determined with a glass electrode. As these methods differ, a conversion of the data had to be undertaken on the basis of available correlation analyses (Höhle et al. 2018), so that the data are comparable and standardized to NFSI II methodology.
The effective cation exchange capacity (ECEC) and the exchangeable cations were determined by percolation of the dried and sieved samples with 1 M NH4Cl solution and subsequent measurement of the cations in the extract (HFA A3.2.1.1). The federal states of Bavaria (extraction with 0.5 M NH4Cl solution (HFA A3.2.1.7)) and Schleswig-Holstein (percolation with SrCl2 solution (HFA A3.2.1.6)) have used diverging methods for NFSI I. Here a conversion of the data could also be achieved on the basis of available correlation analyses (Höhle et al. 2018), so that the data are comparable. The total cation exchange capacity (TCEC) of samples containing carbonate with pH(H2O) >6.2 was determined by percolation with a BaCl2 triethanolamine solution and BaCl2 solution as well as re-exchange of the barium (Ba) ions with a MgCl2 solution and subsequent measurement of the cations in the extract and the re-exchange extract (Ba) (HFA A3.2.1.2); state-specific modifications are described in the report (Höhle et al. 2018). In the humus layer, the cation exchange capacity (CEC) was only determined for NFSI II. This was done by percolation of sieved samples mixed with quartz sand with a 0.1 M BaCl2 solution and subsequent measurement of the cations in the extract (HFA A3.2.1.9).
Diverse methods had been acceptable for the determination of organic C for NFSI I: (1) elemental analysis with elemental analysers (HFA D31.2.1.1–D31.2.2.4), (2) dry combustion with subsequent conductometric CO2 determination according to Wösthoff, (3) indirect estimation via loss of ignition at 550 °C and factor correction (factor 1.72 for mineral soil and 2 for organic layers) and (4) wet combustion with K dichromate and sulphuric acid with subsequent photometric chromium (III) determination. For NFSI II elemental analysis, only elemental analysers were used (HFA D31.2.1.1–D31.2.2.4). The four methods used for NFSI I are regarded as comparable. This is shown by the preliminary study of NFSI II (Evers et al. 2002), in which NFSI I samples were re-analysed with elemental analysers, for methods (2) and (3) and also by a study by the Ökologisches Labor der FHS Eberswalde (Russ and Riek 2011) for method (4). NFSI I carbonate determination was carried out gas volumetrically according to Scheibler (HFA D31.3.1.1). For NFSI II this was done with elemental analysers (HFA D31.3.1.2, D31.3.1.3, D31.3.1.7) or gas volumetrically according to Scheibler (HFA D31.3.1.1). The results are comparable.
Nitrogen was measured in NFSI I through elemental analysis with elemental analysers (HFA D581–D58.1.2.1) or through Kjeldahl digestion with subsequent photometric or titrimetric determination. For NFSI II only elemental analysers were used (HFA D581–D58.1.2.1). The Kjeldahl method is considered to be comparable to elemental analysis. This is shown by the preliminary study of NFSI II (Evers et al. 2002; HFA D581–D58.1.2.1), in which NFSI I samples were re-analysed with elemental analysers.
For the determination of long-term available nutrients and heavy metals, four methods of analysis were permitted for NFSI I to determine Al, calcium (Ca ), Fe , K, magnesium (Mg ), Mn and phosphorus (P) concentration, as well as that of the heavy metals cadmium (Cd), copper (Cu), lead (Pb) and Zn in the humus layer and P in the mineral soil: (1) aqua regia extract (HFA A3.3.3), (2) nitric acid pressure digestion (HFA A3.3.4), (3) perchloric acid digestion and (4) total digestion with hydrogen-fluoride addition (HFA A3.3.1, A3.3.2, A3.3.5, A3.3.6). Elemental determination in the digestion solutions were done by ICP, ICP-MS, AAS and spectrophotometric methods. The ring tests that accompanied NFSI I (König and Wolff 1993) showed that the four permitted methods for humus sample digestion for NFSI I provided no nationally comparable data, as there were standard deviations of up to 35% and maximum deviations of up to 160%. Hence the possibility of nationwide evaluation of the data was limited. In order to ensure nationwide comparability of element concentration as well as comparability between first (NFSI I) and subsequent (NFSI II) inventory, the NFSI I retention samples were subjected to aqua regia digestion according to HFA A3.3.3, and the solution then analysed once more. Now all data gained from aqua regia extracts can be compared to another, except the K values, which are heavily dependent on the gradation of the ground samples.
The water 1:2 extract yielded information on soil solution properties . The dried and sieved mineral soil samples were mixed 1:2 in proportion to their weight with demineralized water, allowed to stand for 24 h and then filtered (HFA A3.2.2.1). For the element determination in the extracts, element-specific methods such as ICP, ICP-MS, ion chromatography and photometry were used according to HFA, section D. The concentrations from the 1:2 extract are supposed to mirror the properties of the soil solution below the root area. Schlotter et al. (2009) have, however, shown that this is not so with most cations. For the NO3 concentrations in the 1:2 extract, there is a good correlation to the values from the soil solution (suction lysimeters) after standardization of the measured values on the water-soil ratios of field-fresh samples (Evers et al. 2002; Kohlpaintner et al. 2012). For more details see Chap. 5.
Oxalate extracts yielded information on occluded Fe oxides. For this, an extraction with 0.2 M ammonium-oxalate solution in a soil solution ratio of 1:50 was carried out with the dried and sieved soil samples and Fe and Al measured with ICP, ICP-MS or AAS (HFA 3.2.3.1). This method was restricted to NFSI II.
1.12 Sampling of Leaves and Needles
It was mandatory to sample needle or leaves of the four main tree species beech, spruce, pine and oak at each plot. Sampling other tree species was optional. At least five trees should be sampled from the main species within a stand. A detailed description of the sampling method is described in Wellbrock et al. (2006). The sampling design is comparable to ICP Forest Manual Part XII.
1.13 Chemical Analysis of Leaves and Needles
For NFSI I total N concentration determination, two methods were admitted: (1) elemental analysis with elemental analysers (HFA D58.1.3.1) and (2) Kjeldahl digestion with subsequent photometric or titrimetric determination. For NFSI II, elemental analysis was carried out with elemental analysers only (HFA D58.1.3.1). The Kjeldahl method is considered to be comparable to element analysis. This is shown by the preliminary study of NFSI II (Evers et al. 2002), in which NFSI I samples were re-analysed with elemental analysis devices.
Chloride (Cl) was determined by the combustion digestion method according to Schöninger (HFA B3.2.2) and Cl measured subsequently in the extract. There is, however, data for only one federal state available.
Five methods were admitted for the NFSI I determination of nutrients Ca , K, Fe , Mg , Mn , P, S, and silicon (Si) and the heavy metals Cd , Cu , Pb and Zn : (1) nitric acid pressure digestion (HFA B3.2.1), (2) total digestion with hydrofluoric acid (HFA B3.2.3), (3) aqua regia digestion and (4) perchloric acid digestion and dry ashing (not for heavy metals). Element determination in the digestion solutions was carried out by ICP, AAS and spectrophotometric methods. For NFSI II nitric acid pressure digestion only was used (HFA B3.2.1); element determination in the digestion solutions was carried out by ICP, AAS and spectrophotometric methods according to HFA, section D. As far as nitric acid digestion was used in NFSI I and NFSI II, the data are comparable. Total digestion is, in part, not comparable for the elements Al and K. All other elements should be comparable, because the digestion methods used cover total concentration.
The determination of 1000 needle dry weight was made by counting from 3 × 50 to 3 × 100 needles, which were then dried at 105 °C and weighed. The weight was then extrapolated to 1000 needles (HA B2.2). The weight of 100 leaves was determined by counting from 50 to 100 leaves, which were then dried at 105 °C and weighed, whereupon the 100 leaf weight was extrapolated (HA B.3).
1.14 Tree Crown Condition
The Forest Condition Survey represents a basic part of the nationwide and Europe-wide forest monitoring besides the NFSI and the Intensive Forest Monitoring (Level II ). In Germany, the condition of forest trees was recorded first in 1984 and has been conducted annually throughout Germany since 1990. The methods are widely harmonized and standardized throughout Germany (Wellbrock et al. 2018) and also throughout Europe (Eichhorn et al. 2016). The survey is performed on the extensive monitoring plots (Level I), which were established wherever the nodes of a 16 × 16 km grid over Europe coincided with forest land cover. In Germany, some federal states performed the Level I sampling on a denser grid in addition to the 16 × 16 km grid (approx. 430 Level I plots). Between 2006 and 2008, the forest condition survey took place nationwide on the denser grid of the NFSI II (mainly 8 × 8 km). In addition, changes of the grid over time occurred, such as spatial shifts of the grid in Bavaria in 2006 and Brandenburg in 2009. The most common sampling design in Germany is a cross cluster with four satellites each of which comprising six trees. Thus, usually 24 trees are assessed at 1 sample plot. The trees are permanently marked. They have to belong to Kraft class 1 (dominant) to 3 (subdominant), and suppressed trees are not sampled. The Forest Condition Survey is primarily based on defoliation, which describes the loss of needles or leaves in the crown of a tree compared to a local or absolute reference tree with full foliage. Defoliation represents the most widely used indicator for the assessment of tree condition and vitality. The estimation of defoliation takes place visually using binoculars, and defoliation is recorded in 5% classes from 0% (no defoliation) to 100% (dead tree). A quality assurance programme including national training courses (Eickenscheidt and Wellbrock 2014; Eichhorn et al. 2016) has been initiated in order to monitor consistency and reproducibility of defoliation data. In addition to defoliation, several other parameters (e.g. discolouration, insect infestation and fructification) are recorded. A detailed description of the survey can be found in Wellbrock et al. (2018) for Germany and in the ICP Forests Manual Part IV (Eichhorn et al. 2016) for Europe.
1.15 Critical Loads
Critical loads of pollutants are defined as the annual deposition below which no long-term harmful effects on ecosystem structure and function are expected according to present knowledge (Nilsson and Grennfelt 1988). Site-specific critical loads were calculated for acidity and for nutrient N after the simple mass balance method (SMB; Sverdrup and de Vries 1994) according to the ICP manual for modelling and mapping (CLRTAP 2016). For a detailed description of critical loads calculation on NFSI plots, see Höhle et al. (2018).
1.15.1 Critical Loads of Acidity
Critical loads of acidifying depositions (CLaci) are calculated from the most important proton sources and sinks (CLRTAP 2016):
where BC are base cations (Ca + Mg + K + Na) while Bc are nutrient cations (Ca + Mg + K), asterisks mark sea salt corrected (Posch et al. 2003, 2015) deposition (subscript dep), and the subscripts w, u, i and de stand for weathering , net growth uptake by harvested trees, immobilization and denitrification , respectively. ANCle,crit is the critical leaching of acid neutralizing capacity . Because sulphur (S) and N depositions both contribute to the acid load, no unique critical loads for either element can be determined. As N sinks cannot compensate S deposition, the maximum critical load for S CLmax(S) is given by:
Equation (1.5) applies only if N depositions are lower than the N sinks (CLmin(N)), i.e. if N dep ≤ CL min(N ) = N i + N u. Together with the maximum critical load for acidifying N (at Sdep = 0) \( {\mathrm{CL}}_{\mathrm{max}}\left(\mathrm{N}\right)={\mathrm{CL}}_{\mathrm{min}}\left(\mathrm{N}\right)+\frac{{\mathrm{CL}}_{\mathrm{max}}\left(\mathrm{S}\right)}{1-{f}_{\mathrm{de}}} \), where f de is the denitrification factor, these quantities define the critical loads function for acidity (CLFaci) for pairs of Ndep and Sdep (CLRTAP 2016).
The leaching (subscript le) of acid neutralizing capacity (ANC ) is defined as:
where Q is the precipitation surplus. The critical leaching of acid neutralizing capacity ANCle,crit is calculated from either a critical proton or Al concentration. Both are related through the gibbsite equilibrium constant K gibb = [Al]/[H]3. The critical limit for Al or hydrogen (H) is chosen from the most vulnerable receptor out of four criteria. (1) To reduce phytotoxic effects, a critical Bc/Al ratio is calculated as weighted mean of tree species-specific tolerated ratios (with growth reductions of approx. 20%; Sverdrup and Warfvinge 1993) for plots on mineral soil and a respective critical Bc/H ratio for plots on peat and peaty mineral soil. To calculate ANCle,crit from these ratios, site-specific nutrient cation leaching is given by Bcle = Bcdep + Bcw − Bcu (CLRTAP 2016). (2) For soils with base saturation >30%, these criteria are not sufficient to conserve base-rich ecosystems. Therefore, a critical pH is set at the lower boundary of the site-specific buffer range (Ulrich 1981; Balla et al. 2013). Buffer range was determined from weighted actual pH(H2O) of the rooted zone. (3) To maintain soil structural stability, Al leaching should not exceed Al weathering , which can be related to base cation weathering by Alw = 2 × BCw (CLRTAP 2016). (4) Vegetation -specific critical limits for base saturation have been derived from the BERN model by Balla et al. (2013). These were converted to critical H concentrations with a GAPON exchange equilibrium (de Vries and Posch 2003; CLRTAP 2016).
1.15.2 Critical Loads of Nutrient Nitrogen for Soils
Critical loads of nutrient N (CLnut(N)) are calculated as (CLRTAP 2016):
The acceptable N leaching Nle,acc is calculated from acceptable N concentrations in soil solution (Ncrit):
The critical limit of N concentration in soil solution (Ncrit) is set for each plot as the minimum of two criteria (Balla et al. 2013; ARGE_StickstoffBW 2014): (1) To prevent vegetation changes, Ncrit(plant) was taken from the BERN model (ARGE_StickstoffBW 2014; Balla et al. 2013) based on CLRTAP (2016) for near-natural forest ecosystems. To this end, NFSI plots were characterized according to their plant sociology based on vegetation relevés (Ziche et al. 2016) and assigned to the reference plant communities of the BERN model (Andreae et al. 2016). Ncrit(plant) was set as 3 mg l−1 for forest plantations. (2) To prevent nutrient imbalances, Ncrit(nut) was derived from the vegetation -specific critical Bc/N ratio after the BERN model (Balla et al. 2013; ARGE_StickstoffBW 2014). For this purpose, nutrient cation concentrations in the rooting zone were calculated from Bcle, Q, available field capacity , soil bulk density and cation exchange capacity from the NFSI II soil samples. Additionally, we compared the results from the described (“modified”) approach to the conservative and save approach where Ncrit is set to 0.2 mg l−1 in broadleaf and 0.4 mg l−1 in coniferous forests to prevent nutrient imbalances (CLRTAP 2016).
Exceedance of Critical Loads
Exceedance of critical loads for pollutant X by atmospheric deposition X dep is defined as:
Exceedance of CLaci depends on two pollutants (S and N) and is defined by the critical loads function CLFaci (CLRTAP 2015, 2016). A multiple-criteria CLF regarding acidifying S and N together with eutrophying N is derived by substituting CLmax(N) through min(CLmax(N), CLnut(N)). Because critical loads are determined to evaluate anthropogenic emissions, the deposition fluxes were sea salt (Posch et al. 2015) corrected.
1.15.3 Derivation of Input Data
Time series of atmospheric deposition of S, N, Ca , Mg , K, Na and Cl as well as sea salt corrected deposition rates (Alveteg et al. 1998) were modelled for each NFSI plot (see Sect. 1.13). To estimate Bcle, we used the long-term mean (1995–2015) total deposition except for the derivation of Ncrit(nut), where only the sea salt born deposition is considered (Balla et al. 2013).
As gibbsite equilibrium constant K gibb, the widely used default value of 300 m6 eq−2 was applied on mineral soils and 100 m6 eq−2 on peat and peaty mineral soils (CLRTAP 2016).
Precipitation surplus (Q), rooting depth (86% cumulated root mass) and available field capacity was estimated for every NFSI plot by von Wilpert et al. (2016).
Bicarbonate concentration ([HCO3]) was calculated from the first dissociation constant, Henry’s constant and a temperature -dependent estimation of CO2 partial pressure according to CLRTAP (2016).
Concentration of dissociated organic acids ([RCOO-]) was estimated according to CLRTAP (2016) from reference concentrations of dissolved organic C (de Vries et al. 2005), an exemplary amount of functional groups per molC (Santore et al. 1995) and a pH-dependent estimate of the first dissociation constant (Oliver et al. 1983).
Base cation weathering rate (BCw) was derived according to Posch et al. (2015) as a function of texture and parent material classes with a temperature correction. The weathering rate of nutrient cations (Bcw) was approximated by multiplying BCw with a soil richness factor (0.7–0.85) dependent on cation exchange capacity and available field capacity to distinguish between poor sandy (0.7) and rich soils (0.85).
Net growth uptake (Nu, Bcu) was calculated based on the average (100 years) increment in wood and bark as estimated from Harmonized Stand Inventory and yield tables (Schober 1975). Recent growth rates are higher due to increased N input (Laubhann et al. 2009) and other environmental factors (Pretzsch et al. 2014); therefore it is recommended to use “old” yield tables for critical load calculations (Posch et al. 2015). Volume increments were transformed in wood and bark mass using wood and bark densities (Ahner et al. 2013) and bark/wood ratios (Rademacher et al. 1999). Element concentrations in biomass compartments were taken from Jacobsen et al. (2002).
Denitrification (Nde) is formulated as deposition-dependent quantity: \( {\mathrm{N}}_{\mathrm{de}}={\mathrm{N}}_{\mathrm{le},\mathrm{acc}}\times \frac{f_{\mathrm{de}}}{1-{f}_{\mathrm{de}}} \). The denitrification factor f de was derived from soil texture and drainage status according to CLRTAP (2016) as described in Andreae et al. (2016).
Long-term N immobilization rate (Ni) was derived from actual N stocks in organic and mineral soil layers (0–90 cm) and estimated soil age (10,000 a for glacial and 24,000 a for periglacial soils according to the extension of the last glacial maximum; Höhle and Wellbrock 2017 ).
1.16 Atmospheric Deposition
Following Thiele et al. (2017), the long-term trends for the deposition of N, S and base cations were calculated with the model MAKEDEP (Alveteg et al. 1998). For details on methodology, see Schaap et al. (2017). To reconstruct the deposition before 2009, we used the regional trend from the EMEP database (Tarrasón and Nyiri 2008) and standard time series from Alveteg et al. (1998). These time series provide only trend information for S and N. For the long-term development of emissions and deposition of Ca , Mg , K and Cl, very little information is available. In addition, there are a number of different local sources of emission that can contribute to the deposition of these elements. These sources can vary widely depending on local and regional factors. This is especially the case for K (Dämmgen et al. 2013a). However, long-term studies of the deposition process (Dämmgen et al. 2013a, b; Hedin et al. 1994; Meesenburg et al. 1995) show that Ca and Mg at least partially follow the trend of S deposition. Therefore, it is assumed that the non-marine portion of the deposition of these elements can at least be partly associated with human activities and have the same trend as the stand S curve (Johansson et al. 1996). For K and Cl, the influence of emission-reducing measures was also considered (Dämmgen et al. 2013a), but this is not quite as pronounced as for S. More details on the assumptions and evaluation are given in Höhle et al. (2016). Examples of this approach to generate time series of N and S are described in Ahrends et al. (2010), Fleck et al. (2017) and Hauck et al. (2012). In Eastern Germany high depositions rates (fly ashes from brown coal-fired power plants) occurred in the 1970s and 1980s and are accordingly no longer relevant for the deposition rates between the two NFSIs but of course for the soil chemical state and its dynamics (Riek et al. 2012).
1.17 Statistics
1.17.1 Weighting
Weighting of the NFSI plots according to the proportion of forest area they represent was carried out in order to receive an area-representative result. Weighting was necessary because grid densities partly deviated from the 8 × 8 km grid. The weighting factors were calculated as follows (see Eq. 1.10):
with:
-
W l = Weighting factor of the NFSI plots in the federal state l
-
A l = Forest area of federal state l
-
n l = Number of NFSI plots in the federal state l
This weighting approach assumes that the plot density within the forested area of a federal state is homogeneous. The proportion of the forest area of a federal state on the forest area of entire Germany was derived from the Corine land cover data 1990 (EEA 2010a) and 2006 (EEA 2010b).
1.17.2 Basic Evaluations
Statistical parameters (e.g. arithmetic means, standard deviations, 10., 25., 50., 75. and 90. percentiles) were estimated for each soil depth layer (organic layer, 0–5 cm, 5–10 cm, 10–30 cm, 30–60 cm, 60–90 cm). An aggregation of soil depth layers, e.g. the entire profile (organic layer and mineral soil up to a maximum of 90 cm soil depth), was conducted for some parameters. For concentration, a weighted aggregation was carried out according to stocks (organic layer stock and fine soil stock). In case of pH values, the values were delogarithmized, and the aggregation was done on basis of the H+ concentration.
Both the soil parameters for the NFSI II and the temporal change of these parameters between the two NFSIs were analysed. The annual rate of change was calculated as difference between the NFSI I and NFSI II divided by the corresponding time difference. Peats and highly organic soils (63 plots) were not considered for the analyses of the temporal changes but for the description of the state at the NFSI II. The majority of the plots have been sampled at both surveys. These plots represent paired samples. Calculation of changes was done for paired samples as well as for the entire collective (paired and unpaired samples). For paired samples, change rates were calculated as the difference of values between NFSI II and NFSI I divided by the number of years between both surveys. For the entire collective, the calculation of the change rates was based on federal state means. Hence, at most 16 values were available for statistical evaluations.
Differences were tested for significance using a weighted differences t-test. The forest-area weighted values of the state at the NFSI II and the temporal changes were presented as boxplots according to soil depths. A solid line indicates the median and a diamond the arithmetic mean. The length of the box reflects the interquartile range. The whiskers represent the lowest or highest value within the 1.5-fold interquartile range starting from the lower or upper quartile. Outliers are not shown but are included in the calculations for the boxplots. Within the boxplots significant differences were indicated by a star. The state at the NFSI II and temporal change rates were furthermore visualized using maps and cumulative frequency distributions. The classification is again based on weighted percentiles. Therefore, in general data of both surveys were used for estimating weighted percentiles; however, in cases where only data of the NFSI II were available, percentiles were calculated from these data.
Furthermore, values were stratified using a number of potential strata alternatively: grouping variables, e.g. forest stand type , types of acidification and liming. The stratification aims at identifying cause-effect relations, and therefore, unweighted values were used. The comparison of means was performed using ANOVA . The group means were compared using Bonferroni corrected t-tests.
Further details on the statistical methods are explained in the respective chapters. Statistical significance is defined at p < 0.05. Results are presented as arithmetic means ± standard error, unless indicated differently. The statistical basis evaluations were conducted using R 3.3.3 (R Core Team 2017) and SAS 9.4. The maps were made using ArcGis 10.3.1 for desktop.
1.17.3 Challenges and Solutions
The derivation of trends in element stocks from element concentration and fine earth content measurements at two points in time is challenging due to the numerous possibilities for measurement errors. High spatial and temporal variability of element concentrations on the same plot, the representativeness of subsamples of sieved soil taken for measurements, the relevance of extremely low concentrations in the deeper soil layers, the difficulty of accurate volumetric estimations of fine earth contents and bulk density of soil samples, the variable accuracy of laboratory measurements at both points in time and the inaccuracy of depth delineations are the main error sources (Vanguelova et al. 2016).
Several measures were taken from the beginning to counteract these error sources in NFSI II:
Spatial and Temporal Variability
Spatial variability on the plot scale was counteracted by sampling repetition on eight satellite points, at least up to a depth of 30 cm and in nearly all of the federal states. Below 30 cm it was allowed to reduce the number of sampling locations to four, and this is in accordance with the expected depth gradient in spatial variability of element concentrations from organic layers to the deeper layers of the mineral soil (Bekele et al. 2013; Wang et al. 2017). In certain cases, however, spatial variability may require even more sampling locations to reach low standard errors (Kirwan et al. 2005; Schrumpf et al. 2011), thereby potentially introducing an unavoidable uncertainty . Also the seasonality of soil processes may introduce uncertainties, since samples needed to be taken throughout all seasons in usually more than 1 year in order to cover all sampling locations. However, these uncertainties are not expected to introduce directed errors, and should thus decrease when means over several plots are reported. Sampling dates were recorded in order to enable later analysis of such influences.
Representativeness of Subsamples
The smallest-scaled part of spatial variability was counteracted by the mere size of soil samples taken in the field (2 cm to 4 cm in diameter), thereby integrating over earthworm burrows , fine root channels and bulk soil. The soil samples produced were, thus, a mixture of material from these origins and were well mixed due to the combination with material from the other satellite points, sieving, milling and drying. In most federal states, the dry samples were stirred when subsamples were taken in order to improve the representativeness of subsamples; only one federal state (North Rhine-Westphalia) employed a sample divider (HFA A1.3.1) in both NFSIs to partition subsamples from whole samples.
Low Concentrations in Deeper Soil Layers
The laboratory-dependent limit of quantification was recorded together with analysis results in order to be able to judge the reliability of very low concentrations.
Accuracy of Fine Earth Stocks and Bulk Density
Fine earth stocks were derived from bulk density and coarse soil fractions that were estimated or measured with different approaches (see Sect. 1.9). It was assumed that change of these parameters between NFSI I and II is negligible, and, therefore, their values were held constant in all evaluations of the paired sample, in most cases employing the NFSI II value.
Variable Accuracy of Laboratory Measurements
The variable accuracy of laboratory measurements at both points in time was investigated by frequently repeated inter-laboratory ring tests that forced laboratories to improve their methods (König and Wolff 1993; Blum and Heinbach 2010; König et al. 2013).
Inaccuracy of Depth Delineations
Due to the operator-dependent delineation of organic layer and upper mineral soil, the evaluation of each respective layer (organic layer and 0–5 cm of mineral soil) was for the most critical parameters compared with a combination of both layers.
References
Ahner J, Ahrends B, Engel F, Hansen J, Hentschel S, Hurling R, Meesenburg H, Mestermacher U, Meyer P, Möhring B, Nagel J, Nagel R, Pape B, Rohde M, Rumpf H, Schmidt M, Schmidt M, Spellmann H, Sutmöller J (2013) Waldentwicklungsszenarien für das Hessische Ried. Entscheidungsunterstützung vor dem Hintergrund sich beschleunigt ändernder Wasserhaushalts-und Klimabedingungen und den Anforderungen aus dem europäischen Schutzgebietssystem Natura 2000. Beiträge aus der Nordwestdeutschen Forstlichen Versuchsanstalt, vol 10. Nordwestdeutsche Forstliche Versuchsanstalt, Göttingen
Ahrends B, Meesenburg H, Döring C, Jansen M (2010) A spatio-temporal modelling approach for assessment of management effects in forest catchments. Status and perspectives of hydrology in small basins. IAHS Publ 336:32–37
Alveteg M, Walse C, Warfvinge P (1998) Reconstructing historic atmospheric deposition and nutrient uptake from present day values using MAKEDEP. Water Air Soil Pollut 104(3–4):269–283. https://doi.org/10.1023/a:1004958027188
Andreae H, Eickenscheidt N, Evers J, Grüneberg E, Ziche D, Ahrends B, Höhle J, Nagel H-D, Wellbrock N (2016) Stickstoffstatus und dessen zeitliche Veränderung in Waldböden. In: Wellbrock N, Bolte A, Flessa H (eds) Dynamik und räumliche Muster forstlicher Standorte in Deutschland: Ergebnisse der Bodenzustandserhebung im Wald 2006 bis 2008, vol Thünen Report 43. Johann Heinrich von Thünen Institute, Federal Research Institute for Rural Areas, Forestry and Fisheries, Braunschweig, pp 135–180
ARGE_StickstoffBW (ed) (2014) Ermittlung standortspezifischer Critical Loads für Stickstoff – Dokumentation der Critical Limits und sonstiger Annahmen zur Berechnung der Critical Loads für bundesdeutsche FFH-Gebiete, vol ID Umweltbeobachtung U26-S7-N12. Arbeitsgemeinschaft Stickstoff, federal state Baden-Württemberg, Karlsruhe
Balla S, Müller-Pfannenstiel K, Uhl R, Kiebel A, Lüttmann J, Lorentz H, Düring I, Schlutow A, Schleuschner T, Förster M, Becker C, Herzog W (2013) Untersuchung und Bewertung von straßenverkehrsbedingten Nährstoffeinträgen in empfindliche Biotope. Forschung Straßenbau und Straßenverkehrstechnik, vol 1099. Federal Highway Research Institute (BASt), Bremen
Bekele A, Kellman L, Beltrami H (2013) Plot level spatial variability of soil organic carbon, nitrogen, and their stable isotopic compositions in temperate managed forest soils of Atlantic Canada. Soil Sci 178(8):400–416. https://doi.org/10.1097/ss.0000000000000003
Blum U, Heinbach R (2010) Gesamtauswertung der Datengrundlage sämtlicher BZE Ringversuche 2005 bis 2009. Bavarian State Institute of Forestry, Freising
Blume H-P, Horn R, Kandeler E, Kögel-Knabner I, Kretzschmar R, Stahr K, Wilke BM (2010) Scheffer/Schachtschabel: Lehrbuch der Bodenkunde. Spektrum Akademischer Verlag, Heidelberg
BMELF (1994) Arbeitsanleitung zur ersten Bodenzustandserhebung im Wald, 2nd edn. Federal Ministry of Food, Agriculture and Forestry, Berlin
Bytnerowicz A, Omasa K, Paoletti E (2007) Integrated effects of air pollution and climate change on forests: a northern hemisphere perspective. Environ Pollut 147(3):438–445. https://doi.org/10.1016/j.envpol.2006.08.028
CLRTAP (2015) Exceedance calculations. In: Manual on methodologies and criteria for modelleding and mapping critical loads and levels and air pollution effects, risks and trends. UNECE Convention on Long-range Transboundary Air Pollution. http://www.icpmapping.org/. Accessed 12 Jan 2018
CLRTAP (2016) Mapping of critical loads for ecosystems. In: Manual on methodologies and criteria for modelling and mapping critical loads and levels and air pollution effects, risks and trends. UNECE Convention on Long-range Transboundary Air Pollution
Dämmgen U, Matschullat J, Zimmermann F, Strogies M, Grünhage L, Scheler B, Conrad J (2013a) Emission reduction effects on bulk and wet-only deposition in Germany – evidence from long-term observations. Part 2: precipitation, potential sea salt, soil and fly ash constituents. Gefahrst Reinhalt Luft 73(1–2):25–36
Dämmgen U, Matschullat J, Zimmermann F, Strogies M, Grünhage L, Scheler B, Conrad J (2013b) Emission reduction effects on bulk and wet-only deposition in Germany – evidence from long-term observations. Part 3: sulphur and nitrogen compounds. Gefahrst Reinhalt Luft 73(7–8):330–339
de Vries W, Posch M (2003) Derivation of cation exchange constants for sand, loess, clay and peat soils on the basis of field measurements in the Netherlands. Alterra report. Soil Science Centre at Wageningen University & Research, Wageningen
de Vries W, Schütze G, Lofts S, Tipping E, Meili M, Römkens PFAM, Groenenberg J (2005) Calculation of critical loads for cadmium, lead and mercury – background document to a mapping manual on critical loads of cadmium, lead and mercury. Alterra report. Soil Science Centre at Wageningen University & Research, Wageningen
EEA (2010a) Raster data on land cover for the CLC 1990 inventory (Version 13 of Feb 2010). European Environment Agency (EEA), Kopenhagen
EEA (2010b) Raster data on land cover for the CLC 2006 inventory (Version 13 of Feb 2010). European Environment Agency (EEA), Kopenhagen
Eichhorn J, Roskams P, Potočić N, Timmermann V, Ferretti M, Mues V, Szepesi A, Durrant D, Seletković I, Schroeck H-W, Nevalainen S, Bussotti F, Paloma G, Wulff S (2016) Part IV visual assessment of crown condition and damaging agents. In: UNECE ICP Forests Programme Co-ordinating Centre (ed) Manual on methods and criteria for harmonized sampling, assessment, monitoring and analysis of the effects of air pollution on forests. Thünen Institute of Forest Ecosystems, Eberswalde, p 54
Eickenscheidt N, Wellbrock N (2014) Consistency of defoliation data of the national training courses for the forest condition survey in Germany from 1992 to 2012. Environ Monit Assess 186(1):257–275. https://doi.org/10.1007/s10661-013-3372-3
Ellenberg H (1971) Integrated experimental ecology: methods and results of ecosystem research in the German Solling Project. In: Ecological studies, vol 2. Springer, Berlin
Evers J, König N, Wolff B, Meiwes KJ (2002) Vorbereitung der Zweiten Bodenzustandserhebung im Wald (BZE II): Untersuchungen zur Laboranalytik, Stickstoffbestimmung und zeitlichen Variabilität bodenchemischer Parameter. Federal Ministry of Food, Agriculture and Consumer Protection, Northwest German Forest Research Institute, Bonn
Fleck S, Ahrends B, Sutmöller J, Albert M, Evers J, Meesenburg H (2017) Is biomass accumulation in forests an option to prevent climate change induced increases in nitrate concentrations in the North German Lowland? Forests 8(6):219
GAFA (ed) (2005) Handbuch Forstliche Analytik (HFA). Grundwerk des Gutachterausschuss forstliche Analytik (GAFA). Federal Ministry of Food, Agriculture and Consumer Protection, Northwest German Forest Research Institute, Bonn
GAFA (ed) (2009) Handbuch Forstliche Analytik (HFA). Grundwerk und 1. - 4. Ergänzung des Gutachterausschuss Forstliche Analytik (GAFA). Bundesministerium für Verbraucherschutz, Ernährung und Landwirtschaft, Bonn
GAFA (ed) (2014) Handbuch Forstliche Analytik (HFA). Grundwerk und 1. - 5. Ergänzung des Gutachterausschuss Forstliche Analytik (GAFA). Federal Ministry of Food, Agriculture and Consumer Protection, Northwest German Forest Research Institute, Bonn
Hauck M, Zimmermann J, Mascha J, Dulamsuren C, Bade C, Ahrends B, Leuschner C (2012) Rapid recovery of stem growth at reduced SO2 levels suggests a major contribution of foliar damage in the pollutant-caused dieback of Norway spruce during the late 20th century. Environ Pollut 164:132–141
Hedin LO, Granat L, Likens GE, Buishand TA, Galloway JN, Butler TJ, Rodhe H (1994) Steep declines in atmospheric base cations in regions of Europe and North-America. Nature 367(6461):351–354. https://doi.org/10.1038/367351a0
Hickler T, Bolte A, Hartard B, Beierkuhnlein C, Blaschke M, Blick T, Brüggemann W, Dorow WHO, Fritze MM, Gregor T, Ibisch P, Kölling C, Kühn I, Musche M, Pompe S, Petercord R, Schweiger O, Seidling W, Trautmann S, Waldenspuhl T, Walentowski H, Wellbrock N (2012) Folgen des Klimawandels für die Biodiversität in Wald und Forst. In: Mosbrugger V, Brasseur GP, Schaller M, Stribrny B (eds) Klimawandel und Biodiversität – Folgen für Deutschland. Wissenschaftliche Buchgesellschaft, Darmstadt, pp 164–221
Hilbrig L, Wellbrock N, Bielefeldt J (2014) Harmonisierte Bestandesinventur: Zweite Bundesweite Bodenzustandserhebung (BZE II) – Methode. Thünen Working Paper. Johann Heinrich von Thünen Institute, Braunschweig. https://doi.org/10.3220/WP_26_2014
Höhle J, Wellbrock N (2017) Immobilisation of nitrogen in context of critical loads – literature review and analysis of German, French and Swiss soil data. Texte 71/2017. Umweltbundesamt, Dessau-Roßlau
Höhle J, Bielefeldt J, Dühnelt P-E, König N, Ziche D, Eickenscheidt N, Grüneberg E, Hilbrig L, Wellbrock N, Kompa T (2018) Bodenzustandserhebung im Wald – Dokumentation und Harmonisierung der Methoden. Thünen Working Paper. Johann Heinrich von Thünen Institute, Braunschweig. https://doi.org/10.3220/WP1526989795000
Höhle J, König N, Hilbrig L, Bielefeld J, Ziche D, Grüneberg E, Eickenscheidt N, Ahrends B, Wellbrock N (2016) Methodenüberblick und Qualitätssicherung. In: Wellbrock N, Bolte A, Flessa H (eds) Dynamik und räumliche Muster forstlicher Standorte in Deutschland. Ergebnisse der Bodenzustandserhebung im Wald 2006 bis 2008, vol Thünen Report 43. Johann Heinrich von Thünen Institute, Federal Research Institute for Rural Areas, Forestry and Fisheries, Braunschweig, pp 6–43
Houba VJG, Chardon WJ, Roelse K (1993) Influence of grinding of soil on apparent chemical composition. Commun Soil Sci Plant Anal 24(13–14):1591–1602. https://doi.org/10.1080/00103629309368902
Jacobsen C, Rademacher P, Meesenburg H, Meiwes K (2002) Gehalte chemischer Elemente in Baumkompartimenten – Literaturstudie und Datensammlung. Berichte des Forschungszentrums Waldökosysteme. Niedersächsische Forstliche Versuchsanstalt Göttingen, Göttingen
Johansson M, Alveteg M, Walse C, Warfvinge P (1996) Derivation of deposition and uptake scenarios. Paper presented at the international workshop on exceedance of critical loads and levels, Vienna
Kauppi P, Anttila P, Kenttämies K (1990) Acidification in Finland. Finnish Acidification Research Programme HAPRO 1985–1990. Springer, Berlin
Kirwan N, Oliver MA, Moffat AJ, Morgan GW (2005) Sampling the soil in long-term forest plots: the implications of spatial variation. Environ Monit Assess 111(1–3):149–172. https://doi.org/10.1007/s10661-005-8219-0
Kohlpaintner M, Huber C, Göttlein A (2012) Improving the precision of estimating nitrate (NO3 −) concentration in seepage water of forests by prestratification with soil samples. Eur J For Res 131(5):1399–1409. https://doi.org/10.1007/s10342-012-0606-9
König N, Wolff B (1993) Abschlussbericht über die Ergebnisse und Konsequenzen der im Rahmen der bundesweiten Bodenzustandserhebung im Wald (BZE) durchgeführten Ringanalysen. Reports of the Research Centre for Forest Ecosystems/Forest Decline – Series B. Göttingen University, Göttingen
König N, Schönfelder E, Blum U (2013) Auswertung der Standardmessungen und der Ringversuche im Rahmen der BZE II. Federal Ministry of Food, Agriculture and Consumer Protection, Berlin
Laubhann D, Sterba H, Reinds GJ, de Vries W (2009) The impact of atmospheric deposition and climate on forest growth in European monitoring plots: an individual tree growth model. For Ecol Manag 258(8):1751–1761. https://doi.org/10.1016/j.foreco.2008.09.050
Leitgeb E, Reiter R, Englisch M, Lüscher P, Schad P, Feger K-H (2013) Waldböden: Ein Bildatlas der wichtigsten Bodentypen aus Österreich, Deutschland und der Schweiz. Wiley-VCH, Weinheim
Meesenburg H, Meiwes KJ, Rademacher P (1995) Long term trends in atmospheric deposition and seepage output in northwest German forest ecosystems. Water Air Soil Pollut 85(2):611–616. https://doi.org/10.1007/bf00476896
Nilsson J, Grennfelt P (1988) Critical loads for sulphur and nitrogen. Workshop on “Critical Loads for the effect on soils and groundwater of long term deposition of nitrogen and sulphur compounds and to establish methods to map the geographical areas experiencing higher than critical loads with respect to the sensitivity of different soil types”. UN-ECE – Nordic Council of Ministers, Skokloster
Oliver BG, Thurman EM, Malcolm RL (1983) The contribution of humic substances to the acidity of colored natural waters. Geochim Cosmochim Acta 47(11):2031–2035
Posch M, Reinds GJ, Slootweg J (2003) The European background database. In: Posch M, Hettelingh J-P, Slootweg J, Downing RJ (eds) Modelling and mapping of critical thresholds in Europe: CCE status report 2003, vol 259101013. National Institute for Public Health and the Environment (RIVM), Bilthoven, pp 37–44
Posch M, de Vries W, Sverdrup HU (2015) Mass balance models to derive critical loads of nitrogen and acidity for terrestrial and aquatic ecosystems. In: de Vries W, Hettelingh JP, Posch M (eds) Critical loads and dynamic risk assessments: nitrogen, acidity and metals in terrestrial and aquatic ecosystems. Environmental pollution, vol 25. Springer, Dordrecht, pp 171–205. https://doi.org/10.1007/978-94-017-9508-1_6
Pretzsch H, Biber P, Schütze G, Uhl E, Rötzer T (2014) Forest stand growth dynamics in Central Europe have accelerated since 1870. Nat Commun 5. https://doi.org/10.1038/ncomms5967
R Core Team (2017) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna
Rademacher P, Buß B, Müller-Using B (1999) Waldbau und Nährstoffmanagement als integrierte Aufgabe in der Kiefernwirtschaft auf ärmeren pleistozänen Sanden. Forst und Holz 54:330–334
Riek W, Russ A, Martin J (2012) Soil acidification and nutrient sustainability of forest ecosystems in the northeastern German lowlands – results of the national forest soil inventory. Folia For Pol Ser A 54(3):187–195. https://doi.org/10.5281/zenodo.30835
Russ A, Riek W (2011) Pedotransferfunktionen zur Ableitung der nutzbaren Feldkapazität–Validierung für Waldböden des nordostdeutschen Tieflands. Waldökologie, Landschaftsforschung und Naturschutz 11:5–17
Santore RC, Driscoll CT, Aloi M (1995) A model of soil organic matter and its function in temperate forest soil development. In: McFee WW, Kelly JM (eds) Carbon forms and functions in forest soils. Soil Science Society America (SSSA), Madison, WI, pp 275–298
Schaap M, Banzhaf S, Scheuschner T, Geupel M, Hendriks C, Kranenburg R, Nagel H-D, Segers AJ, von Schlutow A, Wichink Kruit R, Builtjes PJH (2017) Atmospheric nitrogen deposition to terrestrial ecosystems across Germany, Biogeosciences Discuss. Dessau-Roßlau. https://doi.org/10.5194/bg-2017-491
Schlotter D, Hildebrand EE, Schack-Kirchner H (2009) Die Bodenlösung – Monitor für den Boden oder für die Methode ihrer Gewinnung? Berichte der DBG. German Soil Science Society (DBG), Bonn
Schmidt-Walter P, Ahrends B, Meesenburg H (2017) Wasserhaushalt und Trockenstress für die BWI quantifiziert. AFZ – Der Wald 72(15):36–39
Schober R (1975) Ertragstafeln wichtiger Baumarten bei verschiedener Durchforstung. Sauerländer, Bad Orb
Schrumpf M, Schulze ED, Kaiser K, Schumacher J (2011) How accurately can soil organic carbon stocks and stock changes be quantified by soil inventories? Biogeosciences 8:1193–1212. https://doi.org/10.5194/bg-8-1193-2011
Sverdrup HU, de Vries W (1994) Calculating critical loads for acidity with the simple mass-balance method. Water Air Soil Pollut 72(1–4):143–162. https://doi.org/10.1007/bf01257121
Sverdrup HU, Warfvinge P (1993) The effect of soil acidification on the growth of trees, grass and herbs as expressed by the (Ca+Mg+K)/Al ratio. Reports in ecology and environmental engineering. Lund University, Lund
Tarrasón L, Nyiri Á (2008) Transboundary acidification, eutrophication and ground level ozone in Europe in 2006. EMEP status report. The Meteorological Institute, Oslo
Thiele JC, Nuske RS, Ahrends B, Panferov O, Albert M, Staupendahl K, Junghans U, Jansen M, Saborowski J (2017) Climate change impact assessment – a simulation experiment with Norway spruce for a forest district in Central Europe. Ecol Model 346(2017):30–47
Ulrich B (1981) Destabilisierung von Waldökosystemen durch Akkumulation von Luftverunreinigungen. Der Forst- und Holzwirt 36(21):525–532
Ulrich B (1983) Soil acidity and its relations to acid deposition. In: Ulrich B, Pankrath J (eds) Effects of accumulation of air pollutants in forest ecosystems. Springer, Dordrecht, pp 127–146
Ulrich B (1987) Stability, elasticity, and resilience of terrestrial ecosystems with respect to matter balance. In: Schulze E-D, Zwölfer H (eds) Potentials and limitations of ecosystem analysis. Ecological studies 61. Springer, Berlin, pp 11–49
Vanguelova EI, Bonifacio E, De Vos B, Hoosbeek MR, Berger TW, Vesterdal L, Armolaitis K, Celi L, Dinca L, Kjonaas OJ, Pavlenda P, Pumpanen J, Puttsepp U, Reidy B, Simoncic P, Tobin B, Zhiyanski M (2016) Sources of errors and uncertainties in the assessment of forest soil carbon stocks at different scales-review and recommendations. Environ Monit Assess 188(11):11. https://doi.org/10.1007/s10661-016-5608-5
von Wilpert K, Hartmann P, Puhlmann H, Schmidt-Walter P, Meesenburg H, Müller J, Evers J (2016) Bodenwasserhaushalt und Trockenstress. In: Wellbrock N, Bolte A, Flessa H (eds) Dynamik und räumliche Muster forstlicher Standorte in Deutschland: Ergebnisse der Bodenzustandserhebung im Wald 2006 bis 2008, vol Thünen Report 43. Johann Heinrich von Thünen Institute, Federal Research Institute for Rural Areas, Forestry and Fisheries, Braunschweig, pp 343–386
Wang T, Kang FF, Cheng XQ, Han HR, Bai YC, Ma JY (2017) Spatial variability of organic carbon and total nitrogen in the soils of a subalpine forested catchment at Mt. Taiyue, China. Catena 155:41–52. https://doi.org/10.1016/j.catena.2017.03.004
Wellbrock N, Aydın CT, Block J, Bussian B, Deckert M, Diekmann O, Evers J, Fetzer KD, Gauer J, Gehrmann J, Kölling C, König N, Liesebach M, Martin J, Meiwes KJ, Milbert G, Raben G, Riek W, Schäffer W, Wolff B et al (2006) Bodenzustandserhebung im Wald (BZE II) – Arbeitsanleitung für die Außenaufnahmen. Federal Ministry of Food, Agriculture and Consumer Protection, Bonn
Wellbrock N, Eickenscheidt N, Hilbrig L, Dühnelt P-E, Holzhausen M, Bauer A, Dammann I, Strich S, Engels F, Wauer A (2018) Leitfaden und Dokumentation zur Waldzustandserhebung in Deutschland. Thünen Working Paper, vol 84. Johann Heinrich von Thünen Institute, Braunschweig. https://doi.org/10.3220/WP1513589598000
Wirth C, Schulze E-D, Schwalbe G, Tomczyk S, Weber G, Weller E (2004) Dynamik der Kohlenstoffvorräte in den Wäldern Thüringens. Mitteilungen Thüringer Landesanstalt für Wald, Jagd und Fischerei, Gotha
Ziche D, Michler B, Fischer HS, Kompa T, Höhle J, Hilbrig L, Ewald J (2016) Boden als Grundlage biologischer Vielfalt. In: Wellbrock N, Bolte A, Flessa H (eds) Dynamik und räumliche Muster forstlicher Standorte in Deutschland. Ergebnisse der Bodenzustandserhebung im Wald 2006 bis 2008, vol Thünen Report 43. Johann Heinrich von Thünen Institute, Federal Research Institute for Rural Areas, Forestry and Fisheries, Braunschweig, pp 292–342
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Wellbrock, N. et al. (2019). Concept and Methodology of the National Forest Soil Inventory. In: Wellbrock, N., Bolte, A. (eds) Status and Dynamics of Forests in Germany . Ecological Studies, vol 237. Springer, Cham. https://doi.org/10.1007/978-3-030-15734-0_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-15734-0_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-15732-6
Online ISBN: 978-3-030-15734-0
eBook Packages: Biomedical and Life SciencesBiomedical and Life Sciences (R0)