Abstract
In this note, we review some of the recent developments in the well-posedness theory of nonlinear dispersive partial differential equations with random initial data.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
For conciseness, we restrict our attention to the defocusing case in the following.
- 2.
In fact, there are other critical regularities induced by the Galilean invariance for (1.1.1) and the Lorentzian symmetry for (1.1.2) below which the equations are ill-posed; see [25, 42, 51, 56]. We point out, however, that these additional critical regularities are relevant only when the dimension is low and/or the degree p is small. For example, for NLS (1.1.1) with an algebraic nonlinearity (\(p \in 2\mathbb {N}+ 1\)), the critical regularity induced by the Galilean invariance is relevant (i.e., higher than the scaling-critical regularity \(s_\text {crit}\) in (1.1.4)) only for \(d = 1\) and \(p = 3\). For simplicity, we only consider the scaling-critical regularities in the following.
- 3.
Namely, local-in-time existence of unique solutions almost surely with respect to given random initial data.
- 4.
Hereafter, we use Z to denote various normalizing constants so that the resulting measure is a probability measure provided that it makes sense.
- 5.
Here, we added the mass in the exponent to avoid a problem at the zeroth frequency in (1.2.8) below.
- 6.
In the following, we drop the harmless factor of \(2\pi \).
- 7.
When \( d\ge 3\), it is known that the Gibbs measure \(\rho \) can be constructed only for \(d = 3\) and \(p = 3\). In this case, the resulting Gibbs measure \(\rho \) is not absolutely continuous with respect to the Gaussian measure \(\mu _1\). See [2] for the references therein, regarding the construction of the Gibbs measure (the \(\varPhi ^4_3\) measure) in the real-valued setting.
- 8.
- 9.
In the real-valued setting, we also need to impose that \(g_{ -n} = \overline{g_{n}}\) so that, given a real-valued function \(u_0\), the resulting randomization \(u_0^\omega \) remains real-valued. A similar comment applies to the randomization (1.2.13) introduced for functions on \(\mathbb {R}^d\).
- 10.
See (1.2.16) below for the scaling condition on \(\mathbb {R}^d\).
- 11.
One can choose \(C_\varepsilon = \big (\frac{1}{c} \log \frac{C}{\varepsilon }\big )^\frac{3}{2}\).
- 12.
It is also called the unit-scale randomization in [33].
- 13.
For the local-in-time argument, the defocusing/focusing nature of the equation does not play any role.
- 14.
Needless to say, the solution v is random since it depends on the random linear solution \(z^\omega \). For simplicity, however, we suppress the superscript \(\omega \).
- 15.
Note that, due to the spatial integration in (1.3.17), the largest two frequencies of the dyadic pieces must be comparable.
- 16.
In fact, almost sure norm inflation at \((u_0^\omega , u_1^\omega )\) holds.
- 17.
This argument is not limited to nonlinear dispersive PDEs. For instance, see [45] for an application of this argument in studying a stochastic parabolic PDE.
- 18.
- 19.
Namely, the local existence time depends only on the norm of initial data.
- 20.
- 21.
Here, we assume that \(z_3\) has positive regularity. For example, we know that \(z_3\) has spatial regularity at least \(3\alpha - \frac{9}{2} + 1-\varepsilon \) and hence \(\alpha > \frac{7}{6}\) suffices.
- 22.
Recall the following paraproduct decomposition of the product fg of two functions f and g:
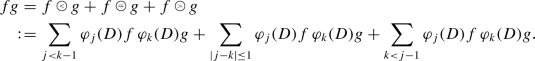
Since the paraproducts
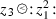 and
and 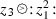 always make sense as distributions, it suffices to give a meaning to the resonant product
always make sense as distributions, it suffices to give a meaning to the resonant product 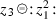 in a probabilistic manner.
in a probabilistic manner. - 23.
- 24.
Things are not as simple as stated here due to the unboundedness of the linear solution operator on \(L^r\), \(r\ne 2\), for dispersive equations. In the case of the nonlinear heat equation, however, this heuristics can be seen more clearly. Consider the following nonlinear heat equation on \(\mathbb {R}^d\):
$$\begin{aligned} \partial _tu = \varDelta u - |u|^{p-1}u \end{aligned}$$(1.4.1)with initial data \(u_0 \in L^2(\mathbb {R}^d)\). In general, (when \(4 < d(p-1)\) for example), we do not know how to construct a solution with initial data in \(L^2(\mathbb {R}^d)\). By randomizing the initial data \(u_0\) as in (1.2.13), we see that the randomized initial data \(u_0^\omega \) lies almost surely in \(L^r(\mathbb {R}^d)\) for any finite \(r\ge 2\). Then, by taking \(r > \frac{d(p-1)}{2}\), we can apply the deterministic subcritical local well-posedness result in [17] to conclude (rather trivial) almost sure local well-posedness of (1.4.1) with respect to the Wiener randomization \(u_0^\omega \). This is an instance of “making the problem subcritical” by randomization.
- 25.
At this point, we do not know how to apply the theory of regularity structures to study dispersive PDEs, partly because we do not know how to lift the Duhamel integral operator for dispersive PDEs to regularity structures.
- 26.
This is the so-called stochastic convolution.
- 27.
For example, for the subcritical SQE on \(\mathbb {T}^3\), the second-order iterate (an analogue of \(z_3\) in (1.3.21)) gains one derivative as compared to the stochastic convolution.
- 28.
References
S. Albeverio, A. Cruzeiro, Global flows with invariant (Gibbs) measures for Euler and Navier-Stokes two dimensional fluids, Comm. Math. Phys. 129 (1990) 431–444.
S. Albeverio, S. Kusuoka The invariant measure and the flow associated to the \(\Phi ^4_3\)-quantum field model, arXiv:1711.07108 [math.PR].
A. Ayache, N. Tzvetkov, \(L^p\)properties for Gaussian random series, Trans. Amer. Math. Soc. 360 (2008), no. 8, 4425–4439.
Á. Bényi, T. Oh, Modulation spaces, Wiener amalgam spaces, and Brownian motions, Adv. Math. 228 (2011), no. 5, 2943–2981.
Á. Bényi, T. Oh, O. Pocovnicu, Wiener randomization on unbounded domains and an application to almost sure well-posedness of NLS, Excursions in harmonic analysis, Vol. 4, 3–25, Appl. Numer. Harmon. Anal., Birkhäuser/Springer, Cham, 2015.
Á. Bényi, T. Oh, O. Pocovnicu, On the probabilistic Cauchy theory of the cubic nonlinear Schrödinger equation on \(\mathbb{R}^3\), \(d\ge 3\), Trans. Amer. Math. Soc. Ser. B 2 (2015), 1–50.
Á. Bényi, T. Oh, O. Pocovnicu, Higher order expansions for the probabilistic local Cauchy theory of the cubic nonlinear Schrödinger equation on \(\mathbb{R}^3\), to appear in Trans. Amer. Math. Soc.
J. Bourgain, Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. I. Schrödinger equations, Geom. Funct. Anal. 3 (1993), 107–156.
J. Bourgain, Periodic nonlinear Schrödinger equation and invariant measures, Comm. Math. Phys. 166 (1994), no. 1, 1–26.
J. Bourgain, Invariant measures for the \(2D\)-defocusing nonlinear Schrödinger equation, Comm. Math. Phys. 176 (1996), no. 2, 421–445.
J. Bourgain, Invariant measures for the Gross-Piatevskii equation, J. Math. Pures Appl. 76 (1997), no. 8, 649–702.
J. Bourgain, Refinements of Strichartz’ inequality and applications to 2D-NLS with critical nonlinearity, Internat. Math. Res. Notices 1998, no. 5, 253–283.
J. Bourgain, A. Bulut, Invariant Gibbs measure evolution for the radial nonlinear wave equation on the 3d ball, J. Funct. Anal. 266 (2014), no. 4, 2319–2340.
J. Bourgain, A. Bulut, Almost sure global well posedness for the radial nonlinear Schrödinger equation on the unit ball I: the 2D case, Ann. Inst. H. Poincaré Anal. Non Linéaire 31 (2014), no. 6, 1267–1288.
J. Bourgain, A. Bulut, Almost sure global well posedness for the radial nonlinear Schrödinger equation on the unit ball II: the 3D case, J. Eur. Math. Soc. (JEMS) 16 (2014), no. 6, 1289–1325.
J. Bourgain, C. Demeter, The proof of the \(l^2\)decoupling conjecture, Ann. of Math. 182 (2015), no. 1, 351–389.
H. Brezis, T. Cazenave, A nonlinear heat equation with singular initial data, J. Anal. Math. 68 (1996), 277–304.
N. Burq, L. Thomann, N. Tzvetkov, Long time dynamics for the one dimensional non linear Schrödinger equation, Ann. Inst. Fourier (Grenoble) 63 (2013), no. 6, 2137–2198.
N. Burq, L. Thomann, N. Tzvetkov, Global infinite energy solutions for the cubic wave equation, Bull. Soc. Math. France 143 (2015), no. 2, 301–313.
N. Burq, L. Thomann, N. Tzvetkov, Remarks on the Gibbs measures for nonlinear dispersive equations, Ann. Fac. Sci. Toulouse Math. 27 (2018), no. 3, 527–597.
N. Burq, N. Tzvetkov, Random data Cauchy theory for supercritical wave equations. I. Local theory, Invent. Math. 173 (2008), no. 3, 449–475.
N. Burq, N. Tzvetkov, Probabilistic well-posedness for the cubic wave equation, J. Eur. Math. Soc. (JEMS) 16 (2014), no. 1, 1–30.
R. Catellier, K. Chouk, Paracontrolled distributions and the 3-dimensional stochastic quantization equation, Ann. Probab. 46 (2018), no. 5, 2621–2679.
A. Choffrut, O. Pocovnicu, Ill-posedness of the cubic nonlinear half-wave equation and other fractional NLS on the real line, Internat. Math. Res. Not. Volume 2018, no.3, 699–738.
M. Christ, J. Colliander, T. Tao, Instability of the periodic nonlinear Schrödinger equation, arXiv:math/0311227v1 [math.AP].
M. Christ, J. Colliander, T. Tao, Ill-posedness for nonlinear Schrödinger and wave equations, arXiv:math/0311048 [math.AP].
J. Colliander, T. Oh, Almost sure well-posedness of the cubic nonlinear Schrödinger equation below \(L^2(\mathbb{T} )\), Duke Math. J. 161 (2012), no. 3, 367–414.
G. Da Prato, A. Debussche, Two-dimensional Navier-Stokes equations driven by a space-time white noise, J. Funct. Anal. 196 (2002), no. 1, 180–210.
G. Da Prato, J. Zabczyk, Stochastic equations in infinite dimensions, Second edition. Encyclopedia of Mathematics and its Applications, 152. Cambridge University Press, Cambridge, 2014. xviii+493 pp.
A. de Bouard, A. Debussche, The stochastic nonlinear Schrödinger equation in \(H^1\), Stochastic Anal. Appl. 21 (2003), no. 1, 97–126.
A.S. de Suzzoni, Large data low regularity scattering results for the wave equation on the Euclidean space, Comm. Partial Differential Equations 38 (2013), no. 1, 1–49.
A.S. de Suzzoni, F. Cacciafesta, Invariance of Gibbs measures under the flows of Hamiltonian equations on the real line, arXiv:1509.02093 [math.AP].
B. Dodson, J. Lührmann, D. Mendelson, Almost sure scattering for the 4D energy-critical defocusing nonlinear wave equation with radial data, arXiv:1703.09655 [math.AP].
B. Dodson, J. Lührmann, D. Mendelson, Almost sure local well-posedness and scattering for the 4D cubic nonlinear Schrödinger equation, arXiv:1802.03795 [math.AP].
H. Feichtinger, Modulation spaces of locally compact Abelian groups, Technical report, University of Vienna (1983). in Proc. Internat. Conf. on Wavelets and Applications (Chennai, 2002), R. Radha, M. Krishna, S. Thangavelu (eds.), New Delhi Allied Publishers (2003), 1–56.
H. Feichtinger and K. Gröchenig, Banach spaces related to integrable group representations and their atomic decompositions, I, J. Func. Anal. 86 (1989), 307–340.
H. Feichtinger and K. Gröchenig, Banach spaces related to integrable group representations and their atomic decompositions, II, Monatsh. Math. 108 (1989), 129–148.
J. Forlano, T. Oh, Y. Wang, Stochastic cubic nonlinear Schrödinger equation with almost space-time white noise, arXiv:1805.08413 [math.AP].
L. Gross, Abstract Wiener spaces, Proc. 5th Berkeley Sym. Math. Stat. Prob. 2 (1965), 31–42.
M. Gubinelli, P. Imkeller, N. Perkowski, Paracontrolled distributions and singular PDEs, Forum Math. Pi 3 (2015), e6, 75 pp.
M. Gubinelli, H. Koch, T. Oh, Renormalization of the two-dimensional stochastic nonlinear wave equations, Trans. Amer. Math. Soc. 370 (2018), no. 10, 7335–7359.
Z. Guo, T. Oh, Non-existence of solutions for the periodic cubic nonlinear Schrödinger equation below \(L^2\), Internat. Math. Res. Not. 2018, no. 6, 1656–1729.
Z. Guo, T. Oh, Y. Wang, Strichartz estimates for Schrödinger equations on irrational tori, Proc. Lond. Math. Soc. 109 (2014), no. 4, 975–1013.
M. Hairer, A theory of regularity structures, Invent. Math. 198 (2014), no. 2, 269–504.
M. Hairer, K. Matetski, Discretisations of rough stochastic PDEs, Ann. Probab. 46 (2018), no. 3, 1651–1709.
J.P. Kahane, Some Random Series of Functions, Second edition. Cambridge Studies in Advanced Mathematics, 5, Cambridge University Press, Cambridge, 1985. xiv+305 pp.
R. Killip, J. Murphy, M. Vişan, Almost sure scattering for the energy-critical NLS with radial data below \(H^1(\mathbb{R}^4)\), to appear in Comm. Partial Differential Equations.
N. Kishimoto, A remark on norm inflation for nonlinear Schrödinger equations, arXiv:1806.10066 [math.AP].
H. Kuo, Gaussian measures in Banach spaces, Lecture Notes in Mathematics, Vol. 463. Springer-Verlag, Berlin-New York, 1975. vi+224 pp.
A. Kupiainen, Renormalization group and stochastic PDEs, Ann. Henri Poincaré 17 (2016), no. 3, 497–535.
H. Lindblad, C. Sogge, On existence and scattering with minimal regularity for semilinear wave equations, J. Funct. Anal. 130 (1995), 357–426.
J. Lührmann, D. Mendelson, Random data Cauchy theory for nonlinear wave equations of power-type on \(\mathbb{R}^3\), Comm. Partial Differential Equations 39 (2014), no. 12, 2262–2283.
J. Lührmann, D. Mendelson, On the almost sure global well-posedness of energy sub-critical nonlinear wave equations on \(\mathbb{R}^3\), New York J. Math. 22 (2016), 209–227.
H.P. McKean, Statistical mechanics of nonlinear wave equations. IV. Cubic Schrödinger, Comm. Math. Phys. 168 (1995), no. 3, 479–491. Erratum: Statistical mechanics of nonlinear wave equations. IV. Cubic Schrödinger, Comm. Math. Phys. 173 (1995), no. 3, 675.
Y. Meyer, Wavelets and operators, Translated from the 1990 French original by D. H. Salinger. Cambridge Studies in Advanced Mathematics, 37. Cambridge University Press, Cambridge, 1992. xvi+224 pp.
L. Molinet, On ill-posedness for the one-dimensional periodic cubic Schrödinger equation, Math. Res. Lett. 16 (2009), no. 1, 111–120.
A. Nahmod, N. Pavlović, G. Staffilani, Gigliola Almost sure existence of global weak solutions for supercritical Navier-Stokes equations, SIAM J. Math. Anal. 45 (2013), no. 6, 3431–3452.
A. Nahmod, G. Staffilani, Almost sure well-posedness for the periodic 3D quintic nonlinear Schrödinger equation below the energy space, J. Eur. Math. Soc. (JEMS) 17 (2015), no. 7, 1687–1759.
E. Nelson, A quartic interaction in two dimensions, 1966 Mathematical Theory of Elementary Particles (Proc. Conf., Dedham, Mass., 1965) pp. 69–73 M.I.T. Press, Cambridge, Mass.
T. Oh, Periodic stochastic Korteweg-de Vries equation with additive space-time white noise, Anal. PDE 2 (2009), no. 3, 281–304.
T. Oh, Remarks on nonlinear smoothing under randomization for the periodic KdV and the cubic Szegö equation, Funkcial. Ekvac. 54 (2011), no. 3, 335–365.
T. Oh, A remark on norm inflation with general initial data for the cubic nonlinear Schrödinger equations in negative Sobolev spaces, Funkcial. Ekvac. 60 (2017) 259–277.
T. Oh, M. Okamoto, O. Pocovnicu, On the probabilistic well-posedness of the nonlinear Schrödinger equations with non-algebraic nonlinearities, arXiv:1708.01568 [math.AP].
T. Oh, M. Okamoto, N. Tzvetkov, Uniqueness and non-uniqueness of the Gaussian free field evolution under the two-dimensional Wick ordered cubic wave equation, preprint.
T. Oh, O. Pocovnicu, Probabilistic global well-posedness of the energy-critical defocusing quintic nonlinear wave equation on \(\mathbb{R}^3\), J. Math. Pures Appl. 105 (2016), 342–366.
T. Oh, O. Pocovnicu, A remark on almost sure global well-posedness of the energy-critical defocusing nonlinear wave equations in the periodic setting, Tohoku Math. J. 69 (2017), no.3, 455–481.
T. Oh, O. Pocovnicu, N. Tzvetkov, Probabilistic local Cauchy theory of the cubic nonlinear wave equation in negative Sobolev spaces, preprint.
T. Oh, O. Pocovnicu, Y. Wang, On the stochastic nonlinear Schrödinger equations with non-smooth additive noise, to appear in Kyoto J. Math.
T. Oh, J. Quastel, On Cameron-Martin theorem and almost sure global existence, Proc. Edinb. Math. Soc. 59 (2016), 483–501.
T. Oh, L. Thomann, A pedestrian approach to the invariant Gibbs measures for the 2-d defocusing nonlinear Schrödinger equations, Stoch. Partial Differ. Equ. Anal. Comput. 6 (2018), 397–445.
T. Oh, L. Thomann, Invariant Gibbs measures for the 2-d defocusing nonlinear wave equations, to appear in Ann. Fac. Sci. Toulouse Math.
T. Oh, N. Tzvetkov, Quasi-invariant Gaussian measures for the cubic fourth order nonlinear Schrödinger equation, Probab. Theory Related Fields 169 (2017), 1121–1168.
T. Oh, N. Tzvetkov, On the transport of Gaussian measures under the flow of Hamiltonian PDEs, Sémin. Équ. Dériv. Partielles. 2015-2016, Exp. No. 6, 9 pp.
T. Oh, N. Tzvetkov, Quasi-invariant Gaussian measures for the two-dimensional defocusing cubic nonlinear wave equation, arXiv:1703.10718 [math.AP].
T. Oh, N. Tzvetkov, Y. Wang, Solving the 4NLS with white noise initial data, preprint.
T. Oh, Y. Wang, On the ill-posedness of the cubic nonlinear Schrödinger equation on the circle, to appear in An. Ştiinţ. Univ. Al. I. Cuza Iaşi. Mat. (N.S.).
T. Ozawa, Y. Tsutsumi, Space-time estimates for null gauge forms and nonlinear Schrödinger equations, Differential Integral Equations 11 (1998), no. 2, 201–222.
R.E.A.C. Paley, A. Zygmund, On some series of functions (1), (2), (3), Proc. Camb. Philos. Soc. 26 (1930), 337–357, 458–474; 28 (1932), 190–205.
O. Pocovnicu, Probabilistic global well-posedness of the energy-critical defocusing cubic nonlinear wave equations on \(\mathbb{R}^4\), J. Eur. Math. Soc. (JEMS) 19 (2017), 2321–2375.
O. Pocovnicu, Y. Wang, An \(L^p\)-theory for almost sure local well-posedness of the nonlinear Schrödinger equations, preprint.
A. Poiret, D. Robert, L. Thomann, Probabilistic global well-posedness for the supercritical nonlinear harmonic oscillator, Anal. PDE 7 (2014), no. 4, 997–1026.
G. Richards, Invariance of the Gibbs measure for the periodic quartic gKdV, Ann. Inst. H. Poincaré Anal. Non Linéaire 33 (2016), no. 3, 699–766.
B. Simon, The \(P(\varphi )_2\)Euclidean (quantum) field theory, Princeton Series in Physics. Princeton University Press, Princeton, N.J., 1974. xx+392 pp.
C. Sun, B. Xia, Probabilistic well-posedness for supercritical wave equations with periodic boundary condition on dimension three, Illinois J. Math. 60 (2016), no. 2, 481–503.
T. Tao, Nonlinear dispersive equations. Local and global analysis, CBMS Regional Conference Series in Mathematics, 106. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 2006. xvi+373 pp.
L. Thomann, N. Tzvetkov, Gibbs measure for the periodic derivative nonlinear Schrödinger equation, Nonlinearity 23 (2010), no. 11, 2771–2791.
N. Tzvetkov, Quasiinvariant Gaussian measures for one-dimensional Hamiltonian partial differential equations, Forum Math. Sigma 3 (2015), e28, 35 pp.
N. Tzvetkov, Random data wave equations, arXiv:1704.01191 [math.AP].
N. Wiener, Tauberian theorems, Ann. of Math. (2) 33 (1932), no. 1, 1–100.
B. Xia, Generic ill-posedness for wave equation of power type on 3D torus, arXiv:1507.07179 [math.AP].
V. Yudovich, Non-stationary flows of an ideal incompressible fluid, Zh. Vychisl. Math. i Math. Fiz. (1963) 1032–1066 (in Russian).
T. Zhang, D. Fang, Random data Cauchy theory for the generalized incompressible Navier-Stokes equations, J. Math. Fluid Mech. 14 (2012), no. 2, 311–324.
Acknowledgements
Á. B. is partially supported by a grant from the Simons Foundation (No. 246024). T. O. was supported by the European Research Council (grant no. 637995 “ProbDynDispEq”). The authors would like to thank Justin Forlano for careful proofreading.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bényi, Á., Oh, T., Pocovnicu, O. (2019). On the Probabilistic Cauchy Theory for Nonlinear Dispersive PDEs. In: Boggiatto, P., et al. Landscapes of Time-Frequency Analysis. Applied and Numerical Harmonic Analysis. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-05210-2_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-05210-2_1
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-05209-6
Online ISBN: 978-3-030-05210-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


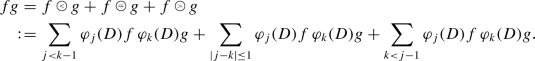
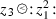 and
and 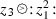 always make sense as distributions, it suffices to give a meaning to the resonant product
always make sense as distributions, it suffices to give a meaning to the resonant product 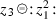 in a probabilistic manner.
in a probabilistic manner.