Abstract
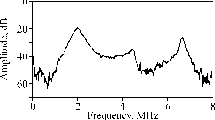
In this paper, the dispersion of surface acoustic waves (SAW) in case carborized steel samples was calculated. The calculations were based on the Thomsen-Haskill matrix formalism. This method has the advantage that it treats a given profile as a stack of several layers, each with arbitrary thickness, density and elastic moduli. This treatment allows for a realistic representation of real material effects by allowing, for example, fluctuations in these parameters with depth, either from material variability or measurement error. In order to demonstrate the capability of the formalism we measured hardness, density and bulk velocity in homogeneously carbonized specimens. We then used these data to synthesize several different hardness profiles, such as might be encountered in actual industrial applications. For these profiles the SAW dispersion curves were then calculated. The results provided valuable insight into such questions as the range of SAW velocity extremal values and the frequency bandwidth over which the velocity changes are maximum. Thus the Thomson- Haskill matrix method is shown to provide a useful tool for simulating the effect of hardness on SAW velocity with potential applications for a wide variety of physical property gradients.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
R.L. Roderick and R. Truell, “The Measurement of Ultrasonic Attenuation in Solids by the Pulse Technique and Some Results in Steel”, J. Appl. Phys., Vol. 23, pp 267–279, 1952.
C. Tamburelli and A. Quaroni, “Ultrasonic Velocity Measurements to Inspect Malleable Iron Casting”, NDT, Vol. 8, pp 152–157, 1975.
N. Bozorg-Grayeli, “Acoustic Nondestructive Evaluation of Microstructure”, Phd. Dissertation, Material Science and Engineering, Stanford University, CA., 1981.
M. Rosen, “Analytical Ultrasonics for Characterization of Metallurgical Microstructure and Transformations”, in Materials Analysis by Ultrasonics, ed. A. Vary, Noyes Data Corp., Park Ridge, New Jersey, USA, pp 79–97, 1987.
J. Krautkramer and H. Krautkramer, Ultrasonic Testing of Materials. 2nd ed., New York, Springer-Verlag, 1977.
S. Singh, P.S. Shuttleworth and H.I.Burrier, “Effects of Carbon Leval and Microstructure on Ultrasonic Velocity in Steels”,in ASNT 1991 Spring Conference. Oakland, CA., USA, pp 140–142.
B.A. Auld, Acoustic Waves and Fields in Solids. Wiley-Interscience, New York, Vol. 2, pp 294, 1974.
B.R. Tittmann and R.B. Thompson, “Measurement of Physical Property Gradients with Elastic Surface Waves”, in Proc. of the Conf. on New NDT Tech.. Southwest Research Institute, San Antonio, Texas, pp 20, April 1973.
B.R. Tittmann, G.A. Alers, R. B. Thompson and R.A. Young, “Characterization of Subsurface Anomalies by Elastic Surface Wave Dispersion”, in Proc. IEEE Ultrasonic Svmp.. Milwaukee, WI, pp 561 - 564, 1974.
J.M. Richardson, “Estimation of surface layer structure from Rayleigh wave dispersion: I. Dense data case”, J. Appl. Phys., Vol. 48, pp 498–512, 1977.
J.M. Richardson and B.R. Tittmann,“Estimation of surface layer structure from Rayleigh wave dispersion: II. Sparse data case-Analytical theory”, J. Appl. Phys., Vol. 48, pp 5111–5121, 1977.
B.R. Tittmann and J.M. Richardson, “Estimation of surface layer structure from Rayleigh wave dispersion: HI. Sparse data case-Interpretation of experimental data”, J. Appl Phys., Vol. 49, pp 5242–5249, 1978.
B.R. Tittmann, L.A. Ahlberg, J.M. Richardson and R.B. Thompson,“Determination of Physical Property Gradients from Measured Surface Wave Dispersion”, IEEE Trans. Ultrason. Ferroelec. Freq. Contr.,Vol. 34, pp 500–507, 1987.
W.T. Thomson “Transmission of Elastic Waves through a Stratified Solid Medium”, J. Appl. Phys., Vol. 21, pp 89, 1950.
N.A. Haskell, “The Dispersion of Surface Waves on Multilayered Media”, Bull Seism. Soc. Am., Vol. 43, pp 17–34, 1953.
K-E Thelning, Steel and its Heat Treatment, 2nd ed., Butterworths, London, 1984.
M. O’Donnell, E.T. Jaynes and J.G. Miller, “Kramers-Kronig relationship between ultrasonic attenuation and phase velocity”, J. Acoust. Soc. Am., Vol 69, pp 696–701, 1981.
E.P. Papadakis, “The Inverse Problem in Materials Characterization through Ultrasonic Attenuation and Velocity Measurements”, in Nondestructive Methods for Material Property Determination, ed. C.O. Ruud and R.E. Green Jr., Plenum Press, New York, pp 151–160, 1984.
J. Kushibiki, H. Asano, T. Ueda and N. Chubachi,“Application of line-focus beam acoustic microscope to inhomogeneity detection of SAW device Materials”, Proc. 1986 !EEE Symposium, 749–753 (1986)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1993 Plenum Press, New York
About this chapter
Cite this chapter
Gordon, G., Tittmann, B., Singh, S. (1993). Surface Acoustic Wave Determination of Hardness: Forward Problem. In: Thompson, D.O., Chimenti, D.E. (eds) Review of Progress in Quantitative Nondestructive Evaluation. Springer, Boston, MA. https://doi.org/10.1007/978-1-4615-2848-7_210
Download citation
DOI: https://doi.org/10.1007/978-1-4615-2848-7_210
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-4613-6233-3
Online ISBN: 978-1-4615-2848-7
eBook Packages: Springer Book Archive