Keywords

1 Introduction

Airborne gravity gradiometry is an advanced technology for surveying a gravity field; it acquires gravity field information with high efficiency and high spatial resolution. Compared with gravity information, the gravity gradient tensor provides more information on the field source such as orientation, depth, and shape (Tang and Hu 2018; Yan and Ma 2015). There are many different types of gravity gradiometer: rotating accelerometer gravity gradiometers, superconducting gravity gradiometers, cold atomic interferometer gravity gradiometers (Paik 2007; Difrancesco 2007; Moody 2011; Liu 2014; Hao 2013). Rotating accelerometer gravity gradiometer (RAGG) was developed by Ernest Metzger of Bell-Aerospace in the 1980s (Heard 1988). But, over the past decade, rotating accelerometer gravity gradiometers are the only commercial moving base gravity gradiometer in the word; all other types are either in fight testing or in a laboratory setting. Companies that operate commercial rotating accelerometer gravity gradiometer systems are: Bell Geospace (Air-FTG), ARKeX (FTGeX), GEDEX (HD-AGG), and FUGRO (AGG-Falcon) (Rogers 2009; Metzger 1977). In this study, we synthetically consider almost all the unperfect factors, for example accelerometer installation errors, accelerometer scale-factor imbalance, etc., and construct a numerical model. The RAGG numerical model is a virtual RAGG with a comprehensive set of precisely adjustable parameters; based on it, many key techniques, for example RAGG automatic calibration, post error compensation, and self-gradient modeling, can be verified.

2 RAGG Numerical Model

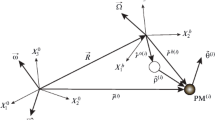
A high-precision numerical model of the RAGG is established, as shown in Fig. 1. In the numerical model, each accelerometer has six mounting error parameters: radial distance, initial phase angle, altitude angle, and misalignment error angles. Among them, the radial distance, initial phase angle, and altitude angle determine the mounting position of the accelerometer; the misalignment error angles determine the orientation deviation between the accelerometer measurement frame and the accelerometer nominal frame of the actual mounting position. The detailed definition of the mounting error parameters can be found in literature (Yu and Cai 2019). Moreover, each accelerometer has nine other output model parameters: zero bias (K j0), linear scale factors (K j1), second-order error coefficients (K j2, K j4, K j5, K j6, K j7, K j8), and current to voltage gain (k jV∕I). We use a test mass to produce gravitational gradients to excite the RAGG. The specific force of the accelerometer A j in the RAGG numerical model is given by:

(1)

Where f cmm is the specific force of the RAGG; \({{\dot {\boldsymbol {\omega }} }_{im}}\) is the angular acceleration of the RAGG with respect to the inertial frame; ω im is the angular velocity of the RAGG with respect to the inertial frame; G is the gravitational constant; \({{{\boldsymbol {r}}_{{o_m}{A_j}}}}\) is the position vector of accelerometer A j in the RAGG measurement frame; m represents the weight of the test mass; and A j S is the position vector from accelerometer A j to the test mass. If the test mass is not a point mass, the gravitational acceleration that the RAGG accelerometers undergo produced by the test mass can be calculated using finite element analysis. In addition, the test mass can be in motion with respect to the RAGG; in this case, A j S is time varying. The specific forces of accelerometer A j in the accelerometer nominal frame of the actual mounting position (f jx, f jy, f jz) can be calculated from:

$$\displaystyle \begin{aligned} {\begin{array}{*{20}{l}} {{f_{jx}} = {{\boldsymbol{f}}_j} \cdot {{\boldsymbol{\tau }}_{jx}}} ,\\ {{f_{jy}} = {{\boldsymbol{f}}_j} \cdot {{\boldsymbol{\tau }}_{jy}}} ,\\ {{f_{jz}} = {{\boldsymbol{f}}_j} \cdot {{\boldsymbol{\tau }}_{jz}}}. \end{array}} \end{aligned} $$
(2)
Fig. 1
figure 1

Principle and program flow of the RAGG numerical model. (a) Principle of the RAGG numerical model. (b) Program flow of the RAGG numerical model

Full size image

Where Ï„ jx, Ï„ jy, and Ï„ jz are unit vectors of the accelerometer nominal frame of the actual mounting position in the directions of the x-, y-, and z-axes. The specific forces in the accelerometer measurement frame are:

$$\displaystyle \begin{aligned} \left[ \begin{matrix} {{f}_{ji}} \\ {{f}_{jo}} \\ {{f}_{jp}} \\ \end{matrix} \right]=\boldsymbol{C}\left[ \begin{matrix} {{f}_{jx}} \\ {{f}_{jy}} \\ {{f}_{jz}} \\ \end{matrix} \right], \end{aligned} $$
(3)

where C is the transformation matrix from the accelerometer nominal frame of the actual mounting position to the accelerometer measurement frame. To make the numerical model approximate the actual RAGG, we add accelerometer noise to the accelerometer model:

(4)

The accelerometer noise f jnoise is simulated by a power spectral density model (Jekeli 2006):

$$\displaystyle \begin{aligned} \varPhi (f)_{noise} = \alpha {f^{ - b}} + {\omega _T} , \end{aligned} $$
(5)

where α and b represent the amplitude and low-frequency growth of the red noise, and ω T denotes the amplitude of the white noise.

Figure 1b is the program flow of the RAGG numerical model. Firstly, the RAGG simulation parameters are set up, including test masses parameters, RAGG rotating disk parameters, accelerometer mounting parameters, accelerometer model parameters, RAGG motion parameters, etc. Then substituting the parameters into the formula (1)–(3) calculates the specific force in accelerometer measurement frame at time t. According to the formula (4), calculating the output voltage of the RAGG accelerometer, the RAGG output before demodulation at time t is calculated by: G out(t) = V 1(t) + V 2(t) − V 3(t) − V 4(t). The above process is repeated until time t is equal to the simulation duration time. Finally, the RAGG output data is input to the quadrature amplitude modulation (QAM) demodulator to extract gravitational gradient.

Let Γ xx, Γ xy, Γ xz, Γ yy, and Γ yz represent the five independent gravitational gradient elements at the origin of the RAGG measurement frame. When mass is far enough away from the RAGG, the gravitational acceleration measured by the RAGG accelerometers is a first-order approximation of the gravitational acceleration and gravitational gradient tensor at the center of the rotating disc; in this case, the inline channel measurement and the cross channel measurement of the RAGG approximate Γ xx − Γ xy and Γ xy; otherwise, the inline channel measurement and cross channel measurement of the RAGG are the sum of Γ xx − Γ xy, Γ xy, and high-order gravitational gradient tensor elements. To distinguish between Γ xx − Γ xy, Γ xy and the measurements of the RAGG, Γ xx − Γ xy, Γ xy is called as center gravitational gradients; Γ xx − Γ xy is the inline channel of the center gravitational gradients; Γ xy is the cross channel of the center gravitational gradients. In RAGG analytical model, gravitational acceleration that the RAGG accelerometer undergoes is a first-order taylor approximation of the gravitational acceleration and gravitational gradient tensor at the center of the rotating disc; but in the numerical model, the gravitational accelerations are calculated using Newton’s law of gravitation instead of a linear approximation. Therefore the numerical model are close to the actual RAGG.

3 Multi-frequency Gravitational Gradient Simulation Experiment

In multi-frequency gravitational gradient simulation experiment, a test mass rotates about the RAGG with time-varying angular velocity producing multi-frequency gravitational gradient excitations. Based on the angular velocity of the test mass and its initial coordinate in the RAGG measurement frame, we can obtain the coordinates of the test mass in the RAGG measurement frame at any time. We then calculate the gravitational gradient tensor at the origin of the RAGG measurement frame and then calculate the center gravitational gradients. The RAGG numerical model simulates a perfect RAGG without accelerometer mounting errors, accelerometer scale-factor imbalances, accelerometer second-order error coefficients and accelerometer noise, so we set the accelerometer mounting errors, the accelerometer second-order error coefficients, accelerometer noise parameters to zero. The linear scale factor of the four accelerometers is k j1 = 10 mA/g, the current-to-voltage gain is k jV∕I = 109 ohm, the nominal mounting radius R is 0.1 m, and the rotation frequency of the RAGG disc is 0.25 Hz. Figure 2 shows a point mass of 486 kg with an initial position in the RAGG measurement frame of (1.1, 0.5, 0) and rotating about the RAGG with time-varying angular speed \(\omega (t)=500+400\sin {}(0.0628t)^\circ /\mathrm {{h}}\).

Fig. 2
figure 2

A test mass rotating about the RAGG with time-varying angular velocity

Full size image

Figure 3 shows the voltage outputs of the four accelerometers in the RAGG numerical model excited by the rotating point mass. Figure 4 shows the output voltage before demodulation of the numerical model. Figures 5 and 6 show the demodulated gravitational gradient comparison among the RAGG model and the center gravitational gradients; we can see that the inline channel and the cross channel of the RAGG numerical model are overlapped with that of the center gravitational gradients and only one curve is displayed; to distinguish the outputs of numerical model and the center gravitational gradients, their differences are calculated and shown in Figs. 7 and 8; the differences are in the order of 10 −1 E, and they are caused by the high-order gravitational gradient tensor.

Fig. 3
figure 3

Accelerometer voltage outputs in RAGG numerical model

Full size image
Fig. 4
figure 4

Output voltage of the numerical model before demodulation

Full size image
Fig. 5
figure 5

Demodulated gravitational gradient comparison between numerical model and center gravitational gradients: Inline channel

Full size image
Fig. 6
figure 6

Demodulated gravitational gradient comparison between numerical model and center gravitational gradients: Cross-channel

Full size image
Fig. 7
figure 7

The difference between center gravitational gradients and numerical model: Inline channel

Full size image
Fig. 8
figure 8

The difference between center gravitational gradients and numerical model: Cross-channel

Full size image

4 Conclusion

Based on the measurement principle and configuration of the RAGG, we considered the factors of circuit gain mismatch, installation error, accelerometer scale-factor imbalance, and accelerometer second-order error coefficients, then developed a high-precision numerical model. The parameters of the RAGG prototypes are unknowable and uncontrollable, but the parameters of the RAGG numerical model are adjustable and knowable; to some extent, the RAGG numerical model are more suitable for verifying some technique solutions of the RAGG.