Skip to main content
Springer Nature Link
Log in

Properties of G1 Continuity Conditions Between Two B-Spline Surfaces

  • Conference paper
Advances in Computer Graphics (CGI 2006)

Part of the book series: Lecture Notes in Computer Science ((LNIP,volume 4035))

Included in the following conference series:

Abstract

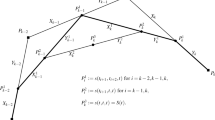
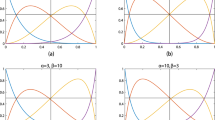
This paper addresses some properties of G 1 continuity conditions between two B-spline surfaces with arbitrary degrees and generally structured knots. Key issues addressed in the paper include necessary G 1 continuity conditions between two B-spline surfaces, general connecting functions, continuities of the general connecting functions, and intrinsic conditions of the general connecting functions along the common boundary. In general, one may use piecewise polynomial functions, i.e. B-spline functions, as connecting functions for G 1 connection of two B-spline surfaces. Based on the work reported in this paper, some recent results in literature using linear connecting functions are special cases of the general connecting functions reported in this paper. In case that the connecting functions are global linear functions along the common boundary commonly used in literature, the common boundary degenerates as a Bézier curve for proper G 1 connection. Several examples for connecting two uniform biquadratic B-spline surfaces with G 1 continuity are also presented to demonstrate the results.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Piegl, L., Tiller, W.: The NURBS Book. Springer, New York (1997)

    Google Scholar 

  2. Milroy, M.J., Bradley, C., Vickers, G.W., Weir, D.J.: G1 continuity of B-spline surface patches in reverse engineering. Computer Aided Design 27(6), 471–478 (1995)

    Article  MATH  Google Scholar 

  3. Ma, W., Leung, P.C., Cheung, E.H.M., Lang, S.Y.T., Cui, H.: Smooth multiple surface fitting for reverse engineering. In: Proceedings of the 32nd CIRP International Seminar on Manufacturing Systems, Katholieke Universteit Leuven, Belgium, pp. 53–62 (1999)

    Google Scholar 

  4. Eck, M., Hoppe, H.: Automatic reconstruction of B-spline surfaces of arbitrary topology type. Computer Graphics 30(8), 325–334 (1996)

    Google Scholar 

  5. Piegl, L.A., Tiller, W.: Filling n-sided regions with NURBS patches. The Visual Computer 15(2), 77–89 (1999)

    Article  MATH  Google Scholar 

  6. Shi, X., Yu, P., Wang, T.: G1 continuous conditions of biquartic B-spline surfaces. Journal of Computational and Applied Mathematics 144(1-2), 251–262 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  7. Shi, X., Wang, T., Yu, P.: A practical construction of G1 smooth biquintic B-spline surfaces over arbitrary topology. Computer Aided Design 36(5), 413–424 (2004)

    Article  MATH  Google Scholar 

  8. Shi, X., Wang, T., Wu, P., Liu, F.: Reconstruction of convergent G1 smooth B-spline surfaces. Computer Aided Geometric Design 21(9), 893–913 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  9. Che, X., Liang, X., Li, Q.: G1 continuity conditions of adjacent NURBS surfaces. Computer Aided Geometric Design 22(4), 285–298 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  10. Che, X., Liang, X.: G1 continuity conditions of B-spline surfaces. Northeastern Math. J. 18, 343–352 (2002)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Hangzhou Dianzi University, Hangzhou, Zhejiang, 310018, P.R. China

    Nailiang Zhao

  2. City University of Hong Kong, Kowloon, Hong Kong SAR, China

    Weiyin Ma

Authors
  1. Nailiang Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weiyin Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. The University of Tokyo,, P.O. Box

    Tomoyuki Nishita

  2. State Key Lab. of CAD&CG, Zhejiang Univerisity,, 310027, Hangzhou, China

    Qunsheng Peng

  3. Max Planck Institute for Computer Science, Saarbrücken, Germany

    Hans-Peter Seidel

Rights and permissions

Reprints and permissions

Copyright information

© 2006 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Zhao, N., Ma, W. (2006). Properties of G1 Continuity Conditions Between Two B-Spline Surfaces. In: Nishita, T., Peng, Q., Seidel, HP. (eds) Advances in Computer Graphics. CGI 2006. Lecture Notes in Computer Science, vol 4035. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11784203_73

Download citation

  • DOI: https://doi.org/10.1007/11784203_73

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-35638-7

  • Online ISBN: 978-3-540-35639-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics