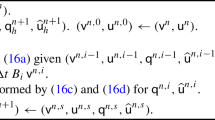1 Introduction

Hyperbolic conservation laws are at the heart of many physical models in science and engineering, e.g., fluid dynamics describing the airflow around an airplane, acoustics, and space plasma modeling. Usually, the systems need to be solved numerically. A common approach is to apply the method of lines, i.e., to apply a spatial semi-discretization first and solve the resulting ordinary differential equation (ODE) numerically. For this task, explicit Runge-Kutta (RK) methods are among the most commonly used schemes because of their efficiency and parallel scalability [48, 53, 55].

Since demanding simulations require a significant amount of compute resources, there is a strong interest in developing efficient numerical methods. Here, the efficiency can be measured by the required compute time, energy, and human time. The time- and energy-to-solution depend on the algorithms and their implementation as well as the hardware [4, 41, 93] and are often a focus of high performance computing (HPC) studies. The required human time depends on the robustness of the overall numerical method and the sensitivity with respect to parameters that may need to be tuned to ensure the robustness and/or the efficiency. In this article, we study an error-based step size control for compressible flow problems to demonstrate that it is efficient in all three aspects.

We use entropy-dissipative semi-discretizations to ensure the robustness [29, 31, 83, 86] but do not investigate specific implementation techniques discussed elsewhere [33, 61, 77]. Instead, we focus on the step size control of time integration methods applied to ODEs resulting from spatial semi-discretizations of compressible flow problems. The goal is to adapt the time step size \(\Delta t\) such that it is as big as possible while still satisfying the accuracy and stability requirements. For explicit RK methods applied to (high-order) semi-discretizations, the stability requirements are usually more restrictive. Thus, a commonly used approach is to adapt the time step size according to a Courant-Friedrichs-Lewy (CFL) number chosen by the user. This involves estimating local wave speeds and mesh spacing, which can be demanding for complex systems and curved high-order meshes in multiple space dimensions required in practice. The optimal CFL number depends on the space and time discretizations and possibly on the specific problem [14, 58, 84]. An alternative, widely used in the context of general-purpose ODE solvers, is an error-based step size control. There, a local error estimate is obtained from an embedded method and fed into a controller adapting the time step size according to user-specified tolerances. This approach has also been used successfully for partial differential equations [6, 51, 74, 94] but appears to be less-widely applied in the CFD community.

In this article, we systematically study an error-based step size control for compressible CFD problems and compare it to CFL-based approaches. Specifically, we use the RK methods and controllers developed in [74] in two different software environments. Most of the examples use the open source packages OrdinaryDiffEq.jl [73] for ODE solvers and Trixi.jl [78, 85] for spatial semi-discretizations implemented in Julia [7]. Some large-scale, industrially relevant CFD simulations are implemented in SSDC [67], which is built on top of the Portable and Extensible Toolkit for Scientific computing (PETSc) [3], its mesh topology abstraction (DMPLEX) [51], and its scalable ODE/DAE solver library [1]. All source code and instructions required to reproduce the numerical experiments using open source packages are available online in our reproducibility repository [79].

In the following, we briefly review RK methods and step size control techniques in Sect. 2. Afterwards, we study the robustness and the sensitivity to user-supplied parameters under a change of mesh structure of both step size control approaches in Sect. 3. Section 4 focuses on the effect of nonlinear shock capturing schemes. In Sect. 5, we discuss the impact of an initial transient period, e.g., in the cold start of a simulation initialized with free stream values. Thereafter, we study the step size control in the presence of a change of variables in Sect. 6. Next, we discuss the convenience of the error-based step size control for exploratory research of new systems in Sect. 7. Finally, we summarize and discuss our findings in Sect. 8.

2 Runge-Kutta (RK) Methods and Step Size Control

We use the method of lines approach and first discretize a conservation law in space. In particular, we focus on spatial semi-discretizations using collocated discontinuous Galerkin (DG) methods (and related shock capturing schemes); see, e.g., [29, 31, 83, 86]. The resulting ODE

$$ \left\{\begin{aligned} \begin{aligned}\frac{\text{d}}{\textrm{d}t} u(t)&= f(t, u(t)),{} & {} t \in (0,T),\\ u(0)&= u^{0} \end{aligned} \end{aligned}\right.$$
(1)

is then solved using numerical time integration methods. Here, we use explicit RK methods with an embedded error estimator of the form [12, 38]

$$\left\{\begin{array} {ll} y_i&= u^n + \Delta t_n \sum _{j=1}^{i-1} a_{ij} \, f(t_n + c_j \Delta t_n, y_j), \qquad i \in \{1, \cdots , s\},\\ u^{n+1}&= u^n + \Delta t_n \sum _{i=1}^{s} b_{i} \, f(t_n + c_i \Delta t_n, y_i), \\ \widehat{u}^{n+1}&= u^n + \Delta t_n \sum _{i=1}^{s} \widehat{b}_{i} \, f(t_n + c_i \Delta t_n, y_i) + \widehat{b}_{s+1} f(t_{n+1}, u^{n+1}). \end{array}\right.$$
(2)

Here, \(u^{n+1}\) is the numerical solution of the main method, \(\widehat{u}^{n+1}\) is the embedded methods solution used to obtain the local error estimate \(u^{n+1} - \widehat{u}^{n+1}\), and \(y_i\) are the stage values. RK methods are parameterized by their Butcher tableau

$$\begin{aligned} \begin{array}{c | c} c &{} A \\ \hline &{} b^{\text{T}} \\ &{} \widehat{b}^{\text{T}} \end{array} \end{aligned}$$
(3)

where \(A = (a_{ij})_{i,j=1}^s \in \mathbb {R}^{s \times s}\) is strictly lower triangular for explicit methods, \(b, c \in \mathbb {R}^s\), and \(\widehat{b}\in \mathbb {R}^{s+1}\). If \(\widehat{b}_{s+1} \ne 0\), the RK pair (2) uses the so-called first-same-as-last (FSAL) idea to include the predicted value at the new time in the embedded error estimator [27]. This can increase the performance of the embedded method and comes at no additional cost if the step is accepted, since \(f(t_{n+1}, u^{n+1})\) must be computed as the first stage of the next step anyway.

All methods considered in this article are applied in the local extrapolation mode, i.e., a main method of order q is coupled with an embedded error estimator of order \(\widehat{q}= q - 1\). Whenever possible, we make use of low-storage formats such as 3S*+ [50, 74]. We use the same naming convention of RK methods as in [74], i.e., NAMEq(\(\widehat{q}\))s indicates an s-stage method of order q with the embedded error estimator of order \(\widehat{q}\). This base name is followed by additional information on low-storage properties and a subscript “F” for FSAL methods.

2.1 Time Integration Loop and Callbacks

We use implementations of the time integration methods available in OrdinaryDiffEq.jl [73] in Julia or PETSc/TS [1]. The basic steps for the time integration loop are given in Algorithm 1. At first, a preliminary time step is performed with the given RK method. If the error-based step size control is activated, the embedded error estimator is also computed; it is used to update the time step size and determine whether the time step is rejected. After accepting a time step, callbacks are activated. We use these callback mechanisms for adaptive mesh refinement (AMR) and, if activated, CFL-based step size control.

figure a

A more detailed overview of the time integration loop is given below in Algorithm 2, discussed after introducing the step size control mechanisms.

2.2 CFL-Based Step Size Control

Explicit time integration methods for first-order hyperbolic conservation laws are subject to a CFL time step restriction of the form \(\Delta t\leqslant C \Delta x/ \lambda _\textrm{max}\) [22]. However, it is non-trivial to provide sharp estimates of the terms in this restriction, e.g., an appropriate value for \(\Delta x\) on curved meshes for high-order DG methods in multiple space dimensions. In general, the CFL-based step size control requires user estimates of the maximal local wave speeds \(\lambda _\textrm{max}(u^n_i)\) at the degree of freedom \(u^n_i\) and the corresponding local mesh spacing \(\Delta x_i\). Then, the time step is determined as

$$\begin{aligned} \Delta t_n = \nu \, \min _i \frac{\Delta x_i}{\lambda _\textrm{max}(u^n_i)}, \end{aligned}$$
(4)

where \(\nu\) is the desired CFL number. For DG methods using polynomials of degree \(p\) on (possibly) curved grids for the linear advection equation \(\partial _t u + (a \cdot \partial _x) u = 0\), we follow [2, 74] and use the estimate

$$\begin{aligned} \frac{\Delta x_i}{\lambda _\textrm{max}(u^n_i)} = \frac{2}{p+ 1} \frac{J_i}{\sum _{j=1}^d\vert (J \partial _{x} \xi ^j)_i \cdot a \vert }, \end{aligned}$$
(5)

where \(d\) is the number of spatial dimensions, \(J_i\) the determinant of the grid Jacobian \(\partial _{x} \xi\) at node i, \((J \partial _{x} \xi ^j)_i\) the contravariant basis vector in direction j at node i [54, Chapter 6], and 2 is the size of the reference element. For nonlinear conservation laws, a is replaced by appropriate estimates of the local wave speeds.

2.3 Error-Based Step Size Control

We perform the error-based step size control based on controller ideas from digital signal processing [36, 37, 88–90]. In particular, we use PID controllers that select a new time step based on

$$\begin{aligned} \Delta t_{n+1} = \kappa \Bigl ( \epsilon _{n+1}^{\beta _1 / k} \epsilon _{n }^{\beta _2 / k} \epsilon _{n-1}^{\beta _3 / k} \Bigr ) \Delta t_{n}, \end{aligned}$$
(6)

where \(k = \min (q, \widehat{q}) + 1\), q is the order of the main method, and \(\widehat{q}\) is the order of the embedded method. Because \(\widehat{q}= q - 1\) in our case, we have that \(k = \widehat{q}+ 1 = q\). Moreover, \(\beta _i\) are the controller parameters, \(\kappa\) is a step size limiter, and

$$\begin{aligned} \epsilon _{n+1} = \frac{1}{w_{n+1}}, \qquad w_{n+1} = \left( \frac{1}{m} \sum _{i=1}^{m} \left( \frac{u_i^{n+1} - \widehat{u}_i^{n+1}}{\tau _a+ \tau _r\max \{ \vert u_i^{n+1}\vert , \vert \widetilde{u}_i\vert \}} \right) ^2 \right) ^{1/2}, \end{aligned}$$
(7)

where m is the total number of degrees of freedom in u, and \(\tau _a, \tau _r\) are the absolute and relative error tolerances. In OrdinaryDiffEq.jl, \(\widetilde{u} = u^{n}\), while PETSc uses \(\widetilde{u} = \widehat{u}^{n+1}\). Unless stated otherwise, we use equal tolerances \(\tau _a= \tau _r= \texttt {tol}\) and the default step size limiter \(\kappa (a) = 1 + \arctan (a - 1)\) [91].

The decision whether the step shall be accepted or rejected is determined by the size of the factor multiplying the time step size \(\Delta t_{n}\) in (6). The default option used for all numerical experiments is to accept a step whenever the limited factor is at least \(0.9^2\). Otherwise, the step is rejected and the time step size \(\Delta t_{n}\) is set as the new predicted step size (6). Another common strategy is to decide whether a step should be rejected based only on the current local error estimate. Söderlind and Wang [89, 91] argued why the approach we described here can be beneficial to reduce the amount of (unnecessary but expensive) step rejections.

To make the step size control fully automatic, we use the estimate of the initial step size implemented in OrdinaryDiffEq.jl from the algorithm described by Hairer et al. [38, p. 169]. \(\epsilon _{n}\) and \(\epsilon _{n-1}\) are initially set to one (for \(n = 0\)).

A more detailed overview of the time integration loop including additional aspects about the step size control and step rejections is shown in Algorithm 2. Parameters such as the threshold \(0.9^2\) used to determine whether a step should be accepted or the limiting threshold \(w_\textrm{min}\) used in Algorithm 2 are based on recommendations in reference works such as [38, Sect. IV.2] and [12, Sect. 371]; we always use their default values and do not consider them as user-facing parameters that need to be chosen manually.

figure b

2.4 Importance of Controller Parameters

The RK pair (2) and the PID controller (6) must be developed together to obtain good results. In particular, semi-discretizations of conservation laws limited by stability should be integrated using a combination of RK pair and controller leading to a stable step size control, based on the test equation [40]; see also [39, Sect. IV.2] and [49]. This has been demonstrated for spectral element discretizations for compressible flows in [74]. In this article, we use the optimized controllers of [74].

2.5 Representative Runge-Kutta (RK) Methods Used in This Article

There is a vast amount of literature on RK methods. Many schemes have been designed as general-purpose methods for low- or high-tolerance applications or even specifically for hyperbolic conservation laws. While we have performed numerical experiments with various schemes, we restrict this article to the following representative set of methods. First, we consider the general-purpose method:

  • \({\textrm{BS}}{3}{(2)}_{\textrm{F}}\), the third-order, three-stage method of [8] (BS3() in OrdinaryDiffEq.jl, 3bs in PETSc).

This method has been shown to be among the most efficient—if not the most efficient—general-purpose method for the CFD problems in which we are interested [74]. Next, we consider methods optimized for spectral element semi-discretizations of compressible CFD, namely,

  • \({\textrm{RDPK}}{3}(2){5}_\textrm{F}[3{\textrm{S}^*}_{+}]\), the third-order, five-stage method of [74] (RDPK3SpFSAL35() in OrdinaryDiffEq.jl);

  • \({\textrm{RDPK}}{4}(3){9}_\textrm{F}[3{\textrm{S}^*}_{+}]\), the fourth-order, nine-stage method of [74] (RDPK3SpFSAL49() in OrdinaryDiffEq.jl).

Finally, we consider the strong stability preserving (SSP) method:

  • \({\textrm{SSP}}3(2)4[3{{\textrm{S}^*}}_{+}]\), the third-order, four-stage SSP method of [57] with embedded method of [21] and efficient implementation and step size controller of [74] (SSPRK43() in OrdinaryDiffEq.jl).

3 Robustness Under Change of Mesh Structure

Both CFL- and error-based step size controls come with parameters that must be chosen by the user, either a CFL factor \(\nu\) or a tolerance \(\texttt {tol}\). However, the sensitivity with respect to these parameters differs significantly. The CFL factor \(\nu\) influences the time step sizes—and thus the efficiency—linearly, while the tolerance \(\texttt {tol}\) has roughly a logarithmic influence. Thus, it is arguably easier to choose an appropriate tolerance than an optimal CFL factor.

Moreover, in the stability limited regime, it is often convenient to use the error-based step size control, since there is usually a range of tolerances resulting in the same number of right-hand side (RHS) evaluations a manually optimized CFL-control could achieve at best. Furthermore, an optimal CFL factor \(\nu\) depends on the mesh. Thus, it can vary when introducing curved coordinates compared to a uniform grid. This was already demonstrated for a 2D linear advection equation in [74, Sect. 3]. Here, we extend this demonstration to the nonlinear compressible Euler equations of an ideal gas in \(d= 3\) space dimensions given by

$$\begin{aligned} \partial _t \begin{pmatrix} \rho \\ \rho v_i \\ \rho e \end{pmatrix} + \sum _{j=1}^d\partial _{x_j} \begin{pmatrix} \rho v_j \\ \rho v_i v_j + p \delta _{ij} \\ (\rho e + p) v_j \end{pmatrix} = 0, \end{aligned}$$
(8)

where \(\rho\) is the density, v the velocity, \(\rho e\) the total energy, and p the pressure given by

$$\begin{aligned} p = (\gamma - 1) \left( \rho e - \frac{1}{2} \rho v^2 \right) , \end{aligned}$$
(9)

with the ratio of specific heats \(\gamma = 1.4\). Specifically, we consider the classical inviscid Taylor-Green vortex with the initial dataFootnote 1

$$\left\{\begin{array} {ll} \rho ^0 = 1, \; v_1^0 = \sin (x_1) \cos (x_2) \cos (x_3), \; v_2^0 = -\cos (x_1) \sin (x_2) \cos (x_3), \; v_3^0 = 0, \\ p^0 = \frac{\rho ^0}{{Ma}^2 \gamma } + \rho ^0 \frac{\cos (2 x_1) \cos (2 x_3) + 2 \cos (2 x_2) + 2 \cos (2 x_1) + \cos (2 x_2) \cos (2 x_3)}{16}, \end{array}\right.$$
(10)

where \({Ma} = 0.1\) is the Mach number. We consider the domain \([-\uppi , \uppi ]^3\) with periodic boundary conditions and meshes with 8 elements per coordinate direction. We apply entropy-dissipative DG methods with polynomials of degree \(p= 3\) using a local Lax-Friedrichs flux at interfaces and the flux of [75, 80, 81] in the volume terms. We integrate the semi-discretizations in the time interval [0, 10].

We consider two meshes, a uniform Cartesian mesh and a curved mesh that heavily warps the Cartesian reference coordinates \((\xi , \eta , \zeta ) \in [-1, 1]^3\) to the desired mesh in physical coordinates (x, y, z) with the mapping

$$\left\{\begin{aligned} y&= \eta + \frac{L_y}{8} \bigl ( \cos (3 \uppi (\xi - c_x) / L_x) \cos ( \uppi (\eta - c_y) / L_y) \cos ( \uppi (\zeta - c_z) / L_z) \bigr ), \\ x&= \xi + \frac{L_x}{8} \bigl ( \cos ( \uppi (\xi - c_x) / L_x) \cos (4 \uppi (y - c_y) / L_y) \cos ( \uppi (\zeta - c_z) / L_z) \bigr ), \\ z&= \zeta + \frac{L_y}{8} \bigl ( \cos ( \uppi (x - c_x) / L_x) \cos (2 \uppi (y - c_y) / L_y) \cos ( \uppi (\zeta - c_z) / L_z) \bigr ), \\&\!\!\!\!L_x = L_y = L_z = 2 \uppi , \quad c_x = c_y = c_z = 0, \end{aligned}\right.$$
(11)

which has been adapted from [17]. The curved mesh and the initial pressure are visualized in Fig. 1.

Fig. 1
figure 1

Initial pressure of the compressible Euler equations for the inviscid Taylor-Green vortex on a slice of the curved mesh

Full size image
Fig. 2
figure 2

Number of ODE RHS evaluations for representative RK methods using error-based (markers) and CFL-based (lines) step size control. The CFL factors were tuned manually to be as large as possible without crashing the simulation. Note that the optimized CFL factors are between 55% and 74% larger on the curved grid

Full size image

The required number of RHS evaluations for the selected, representative RK methods is shown in Fig. 2, for CFL-based and error-based step size controls. All RK methods show the same qualitative behavior on both grids. The step size for this problem is largely limited by the stability, resulting in a range of tolerances yielding the optimal number of RHS evaluations one can also achieve by tuning the CFL factor manually (maximizing \(\nu\) to three significant digits so that the simulations do not crash). This range of tolerances spans up to five orders of magnitude. For looser tolerances, the simulations may crash due to positivity issues, typically in the first few time step. Stricter tolerances let the controller detect an accuracy-limited regime and increase the number of RHS evaluations accordingly. This happens at looser tolerances for \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) than for the other methods, since \({\textrm{SSP}}3(2)4[3{{\textrm{S}^{*}}}_{+}]\) is only optimized for the SSP coefficient, while the other methods are also constructed to minimize the principal truncation error. Since all methods are of the same order of accuracy, the slope of the increasing number of RHS evaluations is the same.

However, there is a significant difference between CFL-based and error-based step size controls when switching the mesh types. Indeed, the CFL factor can be increased between 55% (for \({\textrm{BS}}{3(2)}{3}_{\textrm{F}}\)) and 74% (for \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\)) on the curved mesh compared to the equivalent Cartesian mesh. In particular, choosing an optimized CFL factor from the uniform mesh results in the same amount of efficiency loss when the CFL factor is not tuned again manually from scratch. In contrast, basically, the same range of tolerances can be used to get the optimal number of RHS evaluations on both grids for the error-based step size control.

4 Change of Linear Stability Restrictions in Nonlinear Schemes

There are many shock capturing approaches for DG methods, e.g., artificial viscosity [35, 72], replacing DG elements by finite volume subcells [28, 87], modal filtering [63, 76], or specially constructed invariant domain preserving methods [34, 59, 71]. Here, we use the a priori convex blending of high-order DG elements with finite volume subcells described in [42].

4.1 Linear CFL Restrictions

Shock capturing approaches in nonlinear schemes will typically change the linear CFL restriction on the time step for explicit time integration schemes. Here, we demonstrate this for some third-order schemes of the representative RK methods introduced in Sect. 2.5.

We consider the linear advection equation

$$\begin{aligned} \partial _t u(t,x) + \sum _{j=1}^2 a^j \partial _j u(t,x) = 0 \end{aligned}$$
(12)

in the domain \([-1, 1]^2\) with periodic boundary conditions and velocity \(a = (1, 1)^\text{T} / \sqrt{2}\). We discretize the domain using \(8^2\) uniform elements with polynomials of degree \(p= 3\) on Legendre-Gauss-Lobatto nodes. We choose a fixed blending parameter \(\alpha = 0.5\) in the shock capturing scheme of [42] with the standard DG collocation spectral element method (DGSEM), e.g., [54], and local Lax-Friedrichs flux for the finite volume subcells. We compute the spectra of the standard DGSEM scheme and the shock capturing scheme. Due to the fixed choice of the blending parameter, both semi-discretizations are linear and we compute their spectra numerically.

Fig. 3
figure 3

Spectra of DGSEM and shock capturing (SC) semi-discretizations of the linear advection equation are embedded into the stability regions of some representative RK methods. The stability regions are scaled by the effective number of stages of the RK methods (taking the FSAL property into account). The spectra of the semi-discretizations are scaled by the maximal factor, so that the standard DGSEM spectrum is in the region of absolute stability

Full size image

The spectra embedded into the stability regions of the representative RK methods are visualized in Fig. 3. To make it easier to compare the RK methods, the stability regions are scaled by the effective number of RK stages, taking the FSAL property into account. The spectra of the semi-discretizations are scaled by the maximal factor, so that the standard DGSEM spectrum is in the region of absolute stability of the RK method. Clearly, the (scaled) spectra of the shock capturing semi-discretizations are partially outside of the stability regions. Thus, one can expect a more restrictive CFL condition than for the standard DGSEM schemes.

These linear CFL restrictions predict an approximately one-quarter bigger CFL number for standard DGSEM discretizations compared to the shock capturing variants for \(\textrm{BS}{3}(2){3}_{\textrm{F}}\) and \(\textrm{RDPK}{3}(2){5}_{\textrm{F}}[{\mathrm{3\,S}^*}_{+}]\). For these time integration methods, the SC spectra extend significantly to the left-half of the complex plane outside of the stability regions, in particular near the negative real axis. The effect is qualitatively similar but quantitatively less pronounced for \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) (ca. 5% instead of more than 20%).

4.2 Application to Nonlinear Magnetohydrodynamics: Orszag-Tang Vortex

Next, we apply the representative time integration methods to entropy-dissipative semi-discretizations of the ideal generalized Lagrange multiplier (GLM) magnetohydrodynamics (MHD) equations [9, 25] for the Orszag-Tang vortex setup [66]. Specifically, we use the initial condition

$$\left\{\begin{aligned} \begin{aligned} \rho ^0 = 1, \quad v_1^0 = -\sin (2\uppi x_2), \quad v_2^0 = \sin (2\uppi x_1), \quad v_3^0 = 0, \quad p^0 = 1 / \gamma , \\B_1^0 = -\sin (2\uppi x_2) / \gamma , \quad B_2^0 = \sin (4\uppi x_1) / \gamma , \quad B_3^0 = 0, \quad \psi ^0 = 0, \end{aligned} \end{aligned}\right.$$
(13)

in the domain \([0, 1]^2\) with periodic boundary conditions, where \(\rho\) is the density, v the velocity, p the pressure, B the magnetic field, and \(\psi\) the Lagrange multiplier to control divergence errors. The ideal GLM-MHD equations with ratio of specific heats \(\gamma = 5 / 3\) and divergence cleaning speed \(c_h = 1\) are discretized on a uniform mesh with \(2^6 = 64\) elements per coordinate direction and polynomials of degree \(p= 3\). We use the shock capturing method of [42] with the entropy-conservative numerical flux of [44] and a local Lax-Friedrichs flux at interfaces and for finite volume subcells, both with the nonconservative Powell source term. We use the product of density and pressure as the shock indicator variable with blending parameters \(\alpha _{\textrm{max}} = 0.5\) and \(\alpha _{\textrm{min}} = 0.001\).

Fig. 4
figure 4

Evolution of the density and the shock capturing indicator (SCI) computed using \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) and entropy-dissipative shock capturing semi-discretizations of the ideal GLM-MHD equations for the Orszag-Tang vortex

Full size image

As shown in Fig. 4, the flow and its numerical approximation remain smooth in its initial phase. Between \(t = 0.1\) and \(t = 0.2\), the shock capturing indicator detects troubled cells and activates the finite volume shock capturing mechanism. At the final time, several shocklets are visible in the approximation.

Fig. 5
figure 5

Effective CFL numbers (first row) and time step sizes (second row) of some representative RK methods applied to entropy-dissipative shock capturing semi-discretizations of the ideal GLM-MHD equations for the Orszag-Tang vortex

Full size image

We recorded the time step sizes and effective CFL numbers, i.e., the CFL factor computed a posteriori based on the time step size chosen by the error-based step size controller, after every accepted time step for some representative RK methods. The tolerance is set to \(\texttt {tol}= 10^{-4}\) in all cases with the error-based step size control. For the CFL-based step size control, we bisected the maximal CFL number without blow-up to three significant digits. The results are shown in Fig. 5. Clearly, the time step size of the CFL-based approaches does not vary significantly in time. Thus, the estimated CFL restriction is nearly constant. However, the nonlinear schemes activate shock capturing mechanisms between \(t = 0.1\) and \(t = 0.2\). Thus, the estimated linear CFL restriction should become more severe as discussed in Sect. 4.1. This can be observed also for the error-based step size control; all RK methods use larger time steps initially until the shock capturing part is activated. Then, the error-based step size control yields approximately the maximal step size also used by the CFL-based step size control with manually tuned CFL number. In particular, the initial time step size is approximately one-quarter bigger with the error-based step size control (after the controller has adapted the time step size from the automated initial guess). During the full simulation, the error-based step size control results in the following performance improvements based on the number of function evaluations (see also Table 1): 13% for \(\textrm{BS}{3}(2){3}_{\textrm{F}}\), 11% for \({\textrm{RDPK}}{3}(2){5}_{\textrm{F}}[3{\textrm{S}^{*}}_{+}]\), and 6% for \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\).

While the quantitative numbers for \({\textrm{BS}}{3}(2){3}_{\textrm{F}}\) and \({\textrm{RDPK}}{3}(2){5}_{\textrm{F}}[3{{\textrm{S}}^*}_{+}]\) fit very well to the linear analysis, one could expect that the initial advantage of \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) with the error-based step size control should be smaller, since the stability region is less optimal for high-order DGSEM and relatively better suited for low-order shock capturing methods. First, we do not necessarily expect that such a linear analysis is quantitatively correct for general nonlinear problems, although it was shown to behave very well in applications [70]. Second, the shock capturing mechanism also changes the behavior of the ODE RHS, usually reducing the smoothness of the spatially discrete system, which also affects step size control.

Table 1 Performance of representative RK methods with default error-based and manually tuned CFL-based step size controllers: number of function evaluations (#FE), accepted steps (#A), and rejected steps (#R) for the Orszag-Tang vortex with entropy-dissipative shock capturing semi-discretizations
Full size table

As expected, the method \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\) optimized for spectral element discretizations performs better than the general-purpose method \(\textrm{BS}{3}(2){3}_\textrm{F}\) and uses 15% less function evaluations (with the error-based step size control). For this problem with a significant amount of shock capturing, \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) with error-based step size performs even better and uses additionally 16% less function evaluations than \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\).

In summary, the results of this section demonstrate that the error-based step size control can react robustly and efficiently to varying linear CFL restrictions in nonlinear schemes. In particular, they usually require less parameter tuning while still achieving optimal performance. For this problem with a significant amount of shock capturing mechanisms, the strong stability preserving method \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) performs well.

5 Initial Transient Period: Cold Start of a Simulation

When performing a cold start of a demanding CFD simulation, e.g., by initializing the flow around objects with free stream values, the initial transient period often requires smaller time steps than the fully developed simulation. For demanding simulations with positivity issues for high-order spatial schemes used in this section, we apply SSP time integration methods.

5.1 Double Mach Reflection of a Strong Shock

Fig. 6
figure 6

Density and mesh at the final time of the simulation of the Woodward-Colella double Mach reflection using \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) applied to entropy-dissipative shock capturing semi-discretizations with positivity-preserving limiters and adaptive mesh refinement

Full size image

First, we consider the double Mach reflection of Woodward and Colella [97]. We set up an initial grid with 80 uniform elements that is adaptively refined during the simulation using p4est [11]. We use the shock capturing approach of [42] with DG elements using polynomials of degree \(p= 4\) and the entropy-conservative numerical flux of [75, 80, 81] in the volume terms and a local Lax-Friedrichs flux at interfaces and finite volume subcells. AMR is triggered every two time steps and the positivity-preserving limiter of [99] for density and pressure is applied after every RK stage. We apply \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) to integrate the system in time \(t \in [0, 0.2]\). The complete setup can be found in the reproducibility repository [79]. Figure 6 shows the density and the mesh at the final time.

Fig. 7
figure 7

Time step sizes and effective CFL numbers of \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) applied to entropy-dissipative shock capturing semi-discretizations with positivity-preserving limiters and adaptive mesh refinement for the double Mach reflection problem

Full size image

Figure 7 shows the evolution of the time step sizes and the effective CFL number. There is an initial transient period of ca. 100 time steps where both the time step size and the effective CFL number are much smaller than in the remaining simulation. This small initial step size is selected by the automatic detection algorithm and the error-based step size control, and no manual intervention is necessary. The same simulation setup run with the CFL-based step size control crashes in the first few time steps, even with a small CFL number of \(\nu = 0.01\). The initial transient period can be captured with even smaller CFL numbers, but running the simulation afterwards in a reasonable amount of time required adapting the CFL factor. In contrast, the error-based step size control can be used with the same parameters throughout the simulation.

5.2 Astrophysical Mach 2 000 Jet

Next, we consider a simulation of an astrophysical Mach 2 000 jet using the ideal compressible Euler equations with ratio of specific heat \(\gamma = 5 / 3\) based on the setup of [60]. Specifically, we use the initial condition

$$\begin{aligned} \rho ^0 = 0.5, \quad v_1^0 = 0, \quad v_2^0 = 0, \quad p^0 = 0.417\,2 \end{aligned}$$
(14)

in the domain \([-0.5, 0.5]\) equipped with periodic boundary conditions in the y-direction and Dirichlet boundary conditions using the initial data in the x-direction except for \(t > 0\), \(x =\)− 0.5, and \(y \in [\)− 0.05, 0.05], where we use boundary data (denoted by a superscript b)

$$\begin{aligned} \rho ^\text{b} = 5, \quad v_1^\text{b} = 800, \quad v_2^\text{b} = 0, \quad p^\text{b} = 0.417\,2. \end{aligned}$$
(15)

We use an initially uniform mesh with 64 elements per coordinate direction and polynomials of degree \(p= 3\). We use the shock capturing approach of [42] with the entropy-conservative numerical flux of [75, 80, 81] in the volume terms and a local Lax-Friedrichs flux at interfaces and finite volume subcells. After every time step, we apply adaptive mesh refinement. Moreover, we apply the positivity-preserving limiter of [99] for density and pressure after every RK stage. We integrate the semi-discrete system in time using \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) for \(t \in [0, 10^{-3}]\). The complete setup can be found in the reproducibility repository [79].

Fig. 8
figure 8

Density and mesh at the final time of the simulation of an astrophysical Mach 2 000 jet using \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) applied to entropy-dissipative shock capturing semi-discretizations with positivity-preserving limiters and adaptive mesh refinement

Full size image

Figure 8 shows a snapshot of the numerical solution and the adapted grid at the final time \(t = 10^{-3}\). While the initial condition is given by uniform free stream values, the boundary condition (15) changes the numerical approximation rapidly in time. Consequently, the mesh is refined over time and adapts to the solution structures.

Fig. 9
figure 9

Time step sizes and effective CFL numbers of \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) applied to entropy-dissipative shock capturing semi-discretizations with positivity-preserving limiters and adaptive mesh refinement for the astrophysical Mach 2 000 jet

Full size image

Figure 9 shows the evolution of the time step for this demanding simulation. The initial time step must be very small—of the order \(\Delta t\approx 10^{-12}\)—to allow the simulation to run. For this setup, we set \(\Delta t= 10^{-12}\) initially; other choices are also possible and are adapted to similar values automatically by the controller, but the fully automatic initial guess is not sufficient in this case.

The initial transient period lasts for ca. 100 time steps where the error-based step size controller increases the time step size gradually. Afterwards, the time step size plateaus. Handling such an initial transient period is difficult for standard CFL-based step size controllers. Initially, a CFL factor of \(\nu \approx 10^{-9}\) is required; \(\nu = 10^{-8}\) results in a blow-up of the simulation. One could implement a more complicated CFL-based controller adapting the CFL factor in the initial transient period or restart the simulation after ca. 100 time steps with a larger CFL factor. However, no such additional techniques are required for the error-based step size control, making it easier to use in this case.

5.3 Delta Wing

The next test case setup approximates the solution of the compressible Navier-Stokes equations. We consider an industrially relevant simulation of a 65\(^\circ\) swept delta wing at a Mach number \({Ma} = 0.9\), a Reynolds number \({Re}=10^{6}\) (based on the mean aerodynamic chord), and setting the angle of attack to \(\textrm{AoA}= {13}^\circ\). The geometry was proposed by Hummel and Redeker [47] for the Second International Vortex Flow Experiment (VFE-2) and manufactured based on an NASA wing geometry that served as reference configuration [20]. We consider the flow past the leading-edge configuration with a medium radius leading edge \(r_{\text{LE}}/\bar{c}=0.001\,5\), where \(\bar{c}={0.653}\,{\textrm{m}}\). The delta wing has a mean aerodynamic chord of \(\ell ={0.667}\,{\textrm{m}}\), a root chord length of \(c_{\text{r}} = 1.47 \ell\), and a wing span of \(b=1.37 \ell\). The sting present in the wind tunnel testing is kept downstream as part of the geometry up to the position \(x_1/c_{\text{r}}=1.758\), where the \(x_1\) Cartesian coordinate points in the streamwise direction, as shown in the left part of Fig. 10.

For this test, we use the hp-adaptive entropy-stable solver SSDC [67], which is able to deliver numerical results in good agreement with experimental data. Entropy-stable adiabatic no-slip wall boundary conditions [23] are applied to the wing and sting surfaces, whereas freestream far-field boundary conditions are applied at the inlet and outlet planes. Due to the symmetry of the problem in the span-wise direction, half span of the flow is modeled through a symmetry boundary condition. On the rest of the boundary planes, entropy-stable inviscid wall boundary conditions [69] are prescribed. The grid consists of \(\approx 9.2\times 10^4\) hexahedral elements. It is subdivided into three blocks, as shown in the right part of Fig. 10, with each block corresponding to a different solution polynomial degree p. In particular, we use \(p=2\) in the far-field region, \(p=5\) in the region surrounding the delta wing and its support, and \(p=3\) elsewhere. Given the degree of the solution and the number of elements in each block, the total number of degrees of freedom (DOFs) is \(\approx 1.435 \times 10^{7}\).

Fig. 10
figure 10

Solution polynomial degree distribution, p, computational domain and boundary mesh elements for the 65\(^\circ\) swept delta wing test case [67]

Full size image

The flow around a delta wing is peculiar. When the angle of attack exceeds 7\(^\circ\), typically, flow separation occurs at the leading edge. The roll-up of the leading-edge vortices induces low pressure on the upper surface of the wing and enhances the lift. Figure 11 shows the instantaneous pressure coefficient distribution and streamlines colored by the velocity magnitude at \(t = 0.05\).

Fig. 11
figure 11

Instantaneous pressure coefficient distribution and streamlines colored by the velocity magnitude at \(t = 0.05\) for the 65\(^\circ\) swept delta wing test case [67] (left: top view; right: bottom view)

Full size image
Fig. 12
figure 12

Effective CFL numbers and time step sizes depending on the time step index (left column) and physical time (right column) of some representative RK methods applied to entropy-dissipative semi-discretizations of the compressible Navier-Stokes equations for the delta wing setup

Full size image

Results of simulations using some representative RK methods are shown in Fig. 12. For this cold start of the simulation with free stream values, all methods begin with a conservative estimate of the time step size. The error-based step size controllers increase the time step size in the first few time steps and reach an asymptotically constant step size after a few hundred time steps.

The effective CFL number shown in Fig. 12 is basically proportional to the time step size itself. Running SSDC with the CFL-based step size control requires a CFL factor that is (at least initially)

  • 13% smaller for \(\textrm{BS}{3}(2){3}_\textrm{F}\),

  • 21% smaller for \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\),

  • 32% smaller for \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\),

than the asymptotic CFL factor to avoid a blow-up of the simulation. The required number of RHS evaluations and rejected steps are listed in Table 2.

Table 2 Performance of representative RK methods with error-based step size controllers: number of function evaluations (#FE), accepted steps (#A), and rejected steps (#R) for the delta wing setup up to time \(t = 0.015\)
Full size table

5.4 NASA Common Research Model

The NASA common research model (CRM) was conceived in 2007. Its aerodynamic design was completed in 2008, responding to needs broadly expressed within the US and international aeronautics communities for modern/industry-relevant geometries coupled with advanced experimental data for applied computational fluid dynamic validation studies [82]. Here, we consider the compressible Navier-Stokes equations for a flow over the NASA CRM at an angle of attack of 10\(^\circ\), a Mach number \({Ma} = 0.85\), and a Reynolds number \({Re} = 5 \times 10^{6}\).

The computational domain contains \(12.8 \times 10^{6}\) hexahedral elements with a maximum aspect ratio of approximately 105. Entropy-stable adiabatic no-slip wall boundary conditions [23] are applied to the aircraft, whereas freestream far-field boundary conditions are applied at the inlet and outlet planes. We set a solution polynomial degree \(p = 3\) in the whole domain. Given the degree of the solution and the number of cells, the number of DOFs is \(\approx 7.68 \times 10^{8}\). A zoom of the mesh near the surface of the right wing and the nacelle is shown in Fig. 13.

Fig. 13
figure 13

Zoom of the mesh for the NASA CRM generated at KAUST

Full size image
Fig. 14
figure 14

Effective CFL numbers and time step sizes depending on the time step index (left column) and physical time (right column) of some representative RK methods applied to entropy-dissipative semi-discretizations of the compressible Navier-Stokes equations for the NASA common research model

Full size image

Results of simulations using some representative RK methods are shown in Fig. 14. Again, all methods use a conservative estimate of the initial time step size \(\Delta t\), which then increases \(\Delta t\) monotonically in the first few hundred time steps and reaches an asymptotically approximately constant step size afterwards. The effective CFL number shown in Fig. 14 is, again, basically proportional to the time step size itself. Running SSDC with the CFL-based step size control requires a CFL factor that is (at least initially)

  • 16% smaller for \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\),

  • 9% smaller for \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\),

than the asymptotic CFL factor to avoid a blow-up of the simulation. For \(\textrm{BS}{3}(2){3}_\textrm{F}\), the asymptotic CFL factor from the error-based step size control can be chosen for the complete simulation. The required number of RHS evaluations and rejected steps are listed in Table 3.

Table 3 Performance of representative RK methods with error-based step size controllers: number of function evaluations (#FE), accepted steps (#A), and rejected steps (#R) for the NASA common research model up to time \(t = 0.004\)
Full size table

To conclude this test case, we highlight that the error-based controller yields a substantially higher level of robustness for this industry-relevant test case under a change of mesh structure. To verify that, we simulate the same flow problem using the mesh illustrated in Fig. 15. This new mesh is one of the grids provided for the fifth high-order workshop held at Ceneaero, Belgium, and it corresponds to the mesh tagged as “CRM-WB-a2.75-Coarse-P2A”. When the CFL-based controller is used, the target CFL number is set to the effective asymptotic value obtained from the previous simulations with the mesh shown in Fig. 13, i.e., approximately 3.6 for all three RK methods (see Fig. 14). The simulations run successfully to the final time for all the three time integration methods tested, i.e., \(\textrm{BS}{3}(2){3}_\textrm{F}\), \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\), and \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\), when the error-based time step controller is used. On the contrary, all simulations fail when we choose the CFL-based time step controller. The reason is simple, the effective asymptotic value of the CFL number for this new mesh is approximately a factor of three smaller than the value set, i.e., \(\approx 1.2\). This indicates that the CFL-based controller is not sufficiently robust under a change of mesh. In many cases, we could mitigate the instability by choosing a “very small value” for the target CFL number, but this would yield a very inefficient and computationally expensive time advancement of the simulation.

Fig. 15
figure 15

Zoom of the CRM-WB-a2.75-Coarse-P2A mesh for the NASA CRM provided by the fifth high-order workshop [13]

Full size image

6 Change of Variables: Dissipative Methods Using an Entropy Projection

Whenever a semi-discretization is not strictly a collocation method, there are some transformations between the basic solution variables evolved in time and nodal values required to compute fluxes, e.g., methods using modal coefficients [16, 62], entropy variables as primary unknowns [43, 46], staggered grid methods [56, 68], and DG difference methods [98]. Here, we apply entropy-stable Gauss methods [17] available in Trixi.jl [78, 85] with efficient implementations [77]. While these schemes are more complex than collocation methods due to the entropy projection, they also possess favorable robustness properties for multidimensional simulations of under-resolved compressible flows with variable density and small-scale features [18].

We consider a Kelvin-Helmholtz instability of the 2D compressible Euler equations of an ideal gas with ratio of specific heats \(\gamma = 1.4\) as in [18]. The domain \([-1, 1]^2\) is equipped with periodic boundary conditions and the simulation is initialized with

$$\left\{\begin{aligned} \begin{aligned} \rho _1 = 1, \quad \rho _2 = \rho _1 \frac{1+A}{1-A}, \quad \rho ^0 = \rho _1 + B(x,y) (\rho _2 - \rho _1), \\ p^0 = 1, \quad v_1^0 = B(x,y) - \frac{1}{2}, \quad v_2^0 = \frac{1}{10} \sin (2\uppi x), \end{aligned} \end{aligned}\right.$$
(16)

where A is the Atwood number parameterizing the density contrast and

$$\begin{aligned} B(x,y) = \tanh (15 y + 7.5) - \tanh (15 y - 7.5) \end{aligned}$$
(17)

is a smoothed step function. We apply Gauss methods with 32 elements per coordinate direction and polynomials of degree \(p= 3\). We choose the entropy-conservative flux of [75, 80, 81] for the volume terms and a local Lax-Friedrichs flux at surfaces. We apply several representative RK methods to evolve the resulting entropy-dissipative semi-discretizations in time \(t \in [0, 5]\).

6.1 Mild Initial Conditions with Low Atwood Number

Table 4 Performance of representative RK methods with default error-based and manually tuned CFL-based step size controllers: number of function evaluations (#FE), accepted steps (#A), and rejected steps (#R) for the Kelvin-Helmholtz instability with low Atwood number \(A = 3/7\) and entropy-dissipative Gauss collocation semi-discretizations using entropy projections
Full size table

Table 4 shows a summary of the performance statistics of some representative RK methods for a low Atwood number \(A = 3/7\). The CFL number \(\nu\) was maximized manually up to three significant digits (so that the simulations did not crash). We used time integration methods with controllers recommended in [74] and a default tolerance \(\texttt {tol}= 10^{-4}\); we set \(\texttt {tol}= 10^{-5}\) for \(\textrm{RDPK}{4}(3){9}_\textrm{F}[3{\textrm{S}^{*}}_+]\), since the simulation crashed for the looser default tolerance.

The total number of function evaluations and time steps is always smaller with the error-based step size control in this example, usually around 5%. In addition, the manual optimization of the CFL factor \(\nu\) required several simulation runs. Note that the optimal CFL factors are different from the ones used for the Orzsag-Tang vortex while the same tolerances were used. For this setup, \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) is the most efficient method, followed by \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\).

6.2 Demanding Initial Conditions with High Atwood Number

Increasing the density contrast makes this under-resolved test case more demanding [18]. Violations of positivity are more likely to occur and the sensitivity of the entropy variables for near-vacuum states can cause issues [98, 15]. In particular, the basic variables evolved in time for the Gauss methods violate positivity properties of the density/pressure around \(t \approx 3\) even for strict CFL factors such as \(\nu = 0.05\) for \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\), so that a standard CFL-based step size control is not possible. Similar problems occur for other RK methods.

Table 5 Performance of representative RK methods with default error-based and manually tuned CFL-based step size controllers: number of function evaluations (#FE), accepted steps (#A), and rejected steps (#R) for the Kelvin-Helmholtz instability with high Atwood number \(A = 0.7\) and entropy-dissipative Gauss collocation semi-discretizations using entropy projections
Full size table

In contrast, the error-based step size control works directly in most cases, as shown in Table 5. We only needed to use a stricter tolerance \(\texttt {tol}= 10^{-6}\) for \(\textrm{RDPK}{4}(3){9}_\textrm{F}[3{\textrm{S}^{*}}_+]\). This RK method has more stages than the other methods, making it more difficult to adapt quickly to changing conditions. Again, \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) is the most efficient method, followed by \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\).

7 New Systems: Convenient Exploratory Research

A key feature of error-based time stepping methods is that they require no knowledge of the maximum eigenvalues to select a stable explicit time step. This feature is particularly convenient when one wants to apply the existing numerical methods to new equation systems. To illustrate this, we consider the shallow water equations augmented with an Exner equation to account for interactions between the bottom topography and the fluid flow. The coupled system of equations in two spatial dimensions is

$$\begin{aligned} \frac{\partial }{\partial t} \begin{pmatrix} h\\ hv_1\\ hv_2\\ b \end{pmatrix} + \frac{\partial }{\partial x} \begin{pmatrix} hv_1\\ hv_1^2 + \frac{g}{2}h^2\\ hv_1v_2\\ \xi q_1(\pmb {v}) \end{pmatrix} +\frac{\partial }{\partial y} \begin{pmatrix} hv_2\\ hv_1v_2\\ hv_2^2 + \frac{g}{2}h^2\\ \xi q_2(\pmb {v}) \end{pmatrix} = \begin{pmatrix} 0\\ -gh\frac{\partial b}{\partial x}\\ -gh\frac{\partial b}{\partial y}\\ 0 \end{pmatrix}, \end{aligned}$$
(18)

where h(x, y, t) is the water height, \(\pmb {v}(x,y,t)=(v_1(x,y,t),v_2(x,y,t))^\text{T}\) is the velocity field, b(x, y, t) is the evolving bottom topography, and g is the gravitational constant.

The last line in (18) is the Exner equation for the time evolution of the bottom topography b. It contains the constant \(\xi = 1/(1-\sigma )\) where \(\sigma \in (0,1)\) is the porosity of the bottom material, and the solid transport discharge \(\pmb {q}=(q_1,q_2)^\text{T}\) as a function of the flow velocity \(\pmb {v}\). A closure model is required to describe how the bottom topography couples to the flow and defines the form of the \(\pmb {q}\) terms. This closure depends on the characteristics of the bottom material and flow, e.g., the grain size or Froude number. There exist many closure models for the solid transport discharge proposed and studied (analytically as well as numerically) in the literature; see e.g., [10, 30, 32, 64]. For the present study, we consider the simple and frequently used model due to Grass [32] that models the instantaneous sediment transport as a power law on the velocity field

$$\begin{aligned} \pmb {q}(\pmb {v}) = A_g \pmb {v} \left( v_1^2+v_2^2\right) ^{\frac{m-1}{2}}. \end{aligned}$$
(19)

In (19), the constant \(A_g\in [0,1]\) accounts for the porosity of the bottom sediment layer as well as the effects of the grain size and is usually determined from experimental data. When \(A_g\) is zero, there is no sediment transport and (18) reduces to the standard two-dimensional shallow water equations. The interaction between the bottom and the water flow is weak when \(A_g\) is small and strong as \(A_g\) approaches one. The factor \(m\in [1,4]\) in the Grass model may also be determined from data; however, if one considers odd integer values of m, then (19) can be differentiated and the model remains valid for all values of the velocity field \(\pmb {v}\). For the remainder of this discussion, we will take \(m=3\) and the solid transport discharge will take the form

$$\begin{aligned} \pmb {q}(\pmb {v}) = A_g \pmb {v} \left( v_1^2+v_2^2\right) . \end{aligned}$$
(20)

For the particular closure model (20), we investigate the flux Jacobian of the governing system of equations (18). This is because the choice of a stable explicit time step under a CFL condition requires knowledge of the fastest wave speed of the underlying system. For this, we compute the flux Jacobian in the x-direction, which incorporates non-conservative terms from the right-hand side of (18), to be

$$\begin{aligned} \frac{\partial \pmb {f}}{\partial \pmb {u}} = \begin{pmatrix} 0 &{} 1 &{} 0 &{} 0\\ gh - v_1^2 &{} 2v_1 &{} 0 &{} gh\\ -v_1v_2 &{} v_2 &{} v_1 &{} 0\\ -\frac{3\xi A_g v_1}{h}\left( v_1^2+v_2^2\right) &{} \frac{\xi A_g}{h}\left( 3v_1^2+v_2\right) &{} \frac{2\xi A_g}{h}v_1v_2 &{} 0 \end{pmatrix}. \end{aligned}$$
(21)

Note that the analysis and results in the y-direction are analogous, so we will only consider (21) for this eigenvalue analysis for time step purposes. With the chosen Grass closure model, it has been shown that all the eigenvalues of (21) are real and the governing system (18) is hyperbolic [19, 26]. The eigenvalues of the Jacobian in the x-direction are \(v_1\) and the three roots of the characteristic polynomial

$$\begin{aligned} \lambda ^3 - 2v_1\lambda ^2 + (v_1^2 - gh - g\xi A_g (3v_1^2+v_2^2)) \lambda + g\xi A_gv_1(3v_1^2+v_2^2) =0. \end{aligned}$$
(22)

It is possible, although unwieldy, to apply Cardano’s formula to determine the real, distinct roots of (22). However, an accurate estimate to the maximum wave speed from (22) is necessary for the traditional CFL-based time stepping methods.

For many applications of interest, the characteristic flow speed of the water is much faster than the speed of the bottom topography [19, 45, 92]. In particular, for subcritical flow, the value of \(v_1\) is relatively small, so it is possible to use a loose bound of the flow speeds with \(v_1 \pm \sqrt{gh}\) where \(\sqrt{gh}\) is the surface wave speed. However, this loose bound applied to a CFL time step condition can result in excessive numerical diffusion that acts on the computed (slowly moving) bottom topography.

To approximate the solution of the shallow water equations with an Exner model (18), we use a DG spectral element method in space to create the semi-discretization and apply explicit time integration; see [95] for details. To couple the moving bottom topography b(x, y, t), we use an unsteady approach where the water flow and riverbed are calculated simultaneously. That is, the water flow can be either steady or unsteady and the changes in the bed update are considered to be significant, i.e., the wave speed of the bed-updating equation is of a similar magnitude to the wave speeds of the water flow. For this approach, the system of flow and bottom evolution equations are discretized simultaneously. This high-order DG method applied to the shallow water equations is well balanced for static and subcritical moving water flow [95, 96].

As an exemplary test case, we consider the evolution of a smooth sand hill bottom topography in a uniform flow governed by the shallow water equations. This test case is a two-dimensional numerical simulation that was first proposed and analyzed by de Vriend [24]. It has become a common test case for benchmarking purposes in the moving bottom topography literature, e.g., [5, 19, 26, 45, 92], as it is easy to set up and demonstrates the ability of a numerical scheme to capture the morphology of a bottom topography governed with (18).

It involves the evolution of a conical sand dune in a channel with a non-erodible bottom on a square domain with dimensions 1 000 m \(\times\) 1 000 m. The initial conditions of the flow variables for this test case given in conservative variables are

$$\begin{aligned} \begin{pmatrix} h\\ hv_1\\ hv_2\\ \end{pmatrix} = \begin{pmatrix} 10 -b(x,y,0)\\ 10\\ 0\end{pmatrix}, \end{aligned}$$
(23)

and the initial form of the sediment layer is given by

$$\begin{aligned} b(x,y,0) = {\left\{ \begin{array}{ll} \sin ^2\Bigl (\frac{(x-300)\uppi }{200}\Bigr )\sin ^2\Bigl (\frac{(y-400)\uppi }{200}\Bigr ) &{} \text {if } 300\leqslant x\leqslant 500,\, 400\leqslant y\leqslant 600, \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$
(24)

We set the gravitational constant to be \(g = {9.8}\,{\textrm{m}/\textrm{s}^2}\). The porosity of the sediment material is \(\sigma = 0.4\) and the free parameter from the Grass model (20) is \(A_g = 0.001\). The parameter \(A_g\) corresponds to the coupling strength and speed of interaction between the sediment and the water flow [5, 45]. Taking a small value for \(A_g\) models, weak coupling and a simulation must be run for a longer time period to observe significant variations in the sediment layer. Therefore, we take the final time of this simulation to be \(t = 100\) h (360 000 s). The discharge value \(hv_1= {10}\;{\textrm{m}^2/\textrm{s}}\) from (23) gives the Froude number

$$\begin{aligned} {Fr} = \frac{\sqrt{v_1^2 + v_2^2}}{\sqrt{gh}} \approx 0.1. \end{aligned}$$
(25)

Thus, the flow is in the subcritical regime and we must set boundary conditions accordingly; see, e.g., [65]. For this test case, the boundary conditions are taken to be walls on the top and bottom of the domain, the left is a subcritical inflow, and the right is a subcritical outflow. The complete setup can be found in the reproducibility repository [79].

For the spatial discretization, we divide the domain \(\varOmega = [0,1\,000]^2\) into 900 Cartesian elements. In each element, we use polynomials of degree \(p=5\) in each spatial direction for the DG approximation. This results in 32 400 DOFs for each equation in (18). The classic shallow water equations for water height, momentum, and bottom topography terms are discretized with the well-balanced, high-order DG method described by Wintermeyer et al. [95]. The additional Exner equation for sediment transport is discretized with a standard DG spectral element approximation.

We first investigate the use of the error-based time step control for this shallow water with sediment transport problem setup. We recorded the time step sizes and effective CFL numbers after every accepted time step for three representation RK methods. The tolerance is set to \(\texttt {tol}= 10^{-7}\) for all error-based time stepping methods considered. All three time integration techniques work directly for this test case. The behavior of the time step size and the effective CFL number are presented in Fig. 16. Initially, the time step size of the three methods increases before the time step settles to a stable value as the physical problem becomes a quasi-steady flow where the sediment slowly evolves in the presence of the background flow.

Fig. 16
figure 16

Time step sizes and effective CFL numbers for three error-based RK methods. Left column: # time steps is the x-axis. Right column: time is the x-axis

Full size image

We further investigate the effectiveness of the three time integrators with the error-based step size control for this test case, as shown in Table 6. For this quasi-steady-state configuration, we found that a stricter tolerance \(\texttt {tol}= 10^{-7}\) for all the integration techniques tested performed the best in the sense of requiring a lower number of time steps. Here, we find that \(\textrm{RDPK}{4}(3){9}_\textrm{F}[3{\textrm{S}^{*}}_+]\) is the most efficient method, followed by \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\).

Table 6 Performance of representative RK methods with default error-based and step size controllers: number of function evaluations (#FE), accepted steps (#A), and rejected steps (#R) for a shallow water flow over an evolving sand dune
Full size table

We examine the expected solution behavior as well as simulation results for the sediment transport problem under consideration. As time evolves, the conical dune (24) gradually spreads into a star-shaped pattern. That is, the sediment will redistribute itself along a triangular shape with a particular spreading angle \(\alpha\) and the bulk shape of the dune will move with a speed \(c_0\) as it spreads [24, 45]. This process is illustrated in Fig. 17.

Fig. 17
figure 17

Characteristic evolution of a dune-shaped sediment distribution

Full size image

When the Grass model is used and the interaction between the flow and sediment is weak, that is \(A_g<0.01\), de Vriend [24] derived an analytical approximation for this spreading angle. In particular, when \(m=3\) in the Grass model (20), this spreading angle of a conical dune is

$$\begin{aligned} \alpha = \tan ^{-1}\left( \frac{3\sqrt{3}}{13}\right) \approx {21.787}{^{\circ }}. \end{aligned}$$
(26)

Next, we present simulation results obtained using \(\textrm{RDPK}{4}(3){9}_\textrm{F}[3{\textrm{S}^{*}}_+]\), which was found to be the most efficient. The numerical results from the other two time integration techniques were similar and will not be presented. Figure 18 shows the bottom topography at the initial and final times. From this figure, we see that the discretization captures the expected star-shaped pattern of the sediment evolution.

Fig. 18
figure 18

Projected lateral view of the approximate solution of the bottom topography b(x, y, t) that demonstrates expected star-shaped structure of the conical sand dune at the final time

Full size image

We also estimate the spreading angle of a conical sand dune obtained for the numerical simulation [92]. This is done by examining the angle up to the iso-level 0.012 5 over time, as shown in Fig. 19. We are able to numerically estimate the spreading angle to be \(\alpha _{\text {num}} = {20.4}{^\circ }\). The numerical spreading angle of the current method compares well to the theoretical angle (26) as well as to similar angle studies done in the literature [5, 26, 45, 92].

Fig. 19
figure 19

Estimation of the spreading angle \(\alpha _{\text {num}} = {20.4}{^\circ }\) for the numerical approximation of a conical sand dune found by examining the iso-level 0.012 5 at the initial and final times. The theoretical prediction of the spreading angle for this problem setup is \({21.787}{^\circ }\)

Full size image

We applied error-based time stepping methods to the shallow water equations augmented with an Exner equation to model sediment transport. This served to demonstrate that it is convenient and straightforward to extend the existing code for a new system of equations and obtain a first set of numerical results. This was particularly useful for the considered shallow water Exner equations, because eigenvalue estimates for a general problem setup are unwieldy to obtain [19, 26]. These preliminary results for the evolution and spreading of a conical sand dune compared well to the theoretical solution behavior as well as results from the literature. The development of high-order DG methods for sediment transport problems is the subject of ongoing research. Details about the physical problem setup and numerical parameters as well as all code necessary to reproduce the figures in this section are available in the reproducibility repository for this article [79].

8 Summary and Conclusions

We have compared CFL- and error-based step size controls of explicit RK methods applied to DG semi-discretizations of compressible CFD problems. Our numerical experiments demonstrate that the error-based step size control is convenient and robust in a wide range of applications, including industrially relevant complex geometries with curved meshes in multiple dimensions, shock capturing schemes, initial transient periods (cold start of a simulation), semi-discretizations involving a change of variables, and for exploratory research involving new systems of equations.

There are cures for some problems of the CFL-based step size control discussed in this article. For example, a cold start requiring an initially smaller CFL factor could run a few hundred time steps with a small CFL factor and use a larger CFL factor after a restart—or increase the CFL factor based on a user-supplied function in the first time steps. A change of linear stability behavior of shock capturing schemes could be handled by including the shock capturing indicator in the CFL-based step size control. However, this requires sophisticated additional mechanisms as implemented in some in-house codes. On the other hand, the error-based step size control worked right out of the box without further modifications for the problems considered here. It does not require special handling of many edge cases and comes with a reduced sensitivity with respect to user-supplied parameters.

While we have shown that the error-based step size control is convenient and robust in many applications, including industrially relevant large-scale computations of compressible CFD problems, it does not come with hard mathematical guarantees. For example, some invariant domain preserving methods come with some robustness properties guaranteed under certain CFL constraints; the error-based step size control alone can usually not be proven to satisfy these constraints in all cases. Nevertheless, based on our experience, it is usually robust for suitably chosen shock capturing mechanisms.

As a byproduct of this research, we also compared several time integration methods for hyperbolic conservation laws and compressible flow problems. For lower Mach number flows or problems with positivity issues and/or strong shock capturing requirements, \({\textrm{SSP}}3(2)4[3{\textrm{S}^{*}}_{+}]\) is usually the most efficient scheme. Otherwise, \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3\textrm{S}^{*}_+]\) and \(\textrm{RDPK}{4}(3){9}_\textrm{F}[3{\textrm{S}^{*}}_+]\) are usually the most efficient methods, where \(\textrm{RDPK}{3}(2){5}_\textrm{F}[3{\textrm{S}^{*}}_+]\) tends to be more robust and \(\textrm{RDPK}{4}(3){9}_\textrm{F}[3{\textrm{S}^{*}}_+]\) tends to be more efficient for stricter tolerances. Nevertheless, \(\textrm{BS}{3}(2){3}_\textrm{F}\) is still one of the best general-purpose ODE solvers for problems like the ones considered in this article.

Future research includes the investigation of the error-based step size control with adaptive mesh refinement and stabilization techniques such as positivity-preserving limiters [99]. These are usually implemented as callbacks outside of the inner time integration loop and are thus “not seen” by error estimators. Moreover, we would like to optimize new RK methods including error estimators and step size controllers for compressible CFD problems in other ranges than [2], e.g., focusing on lower Mach flows and dissipative effects.