A Net Present Value Approach in Developing Optimal Replenishment Policies with Allowable Shortages for a Product Life Cycle

Abstract

In this paper, we utilize a net present value approach to devise replenishment policy with allowable shortages in the finite planning horizon by considering a general, time-varying, continuous, deterministic demand function for a product life cycle. We consider four possible alternatives for the inventory problem in the shortage models. (1) It starts with an instant replenishment and ends with zero inventories, (2) It starts with an instant replenishment and ends with shortages, (3) It starts with shortages and ends with zero inventories, or (4) It starts and ends with shortages. We investigate the optimal number of inventory replenishments, the corresponding optimal inventory replenishment time points and the shortage time points and analytically compare these four inventory models based on minimizing the total relevant cost. A complete search procedure is developed to find the optimal solution by employing the properties derived in this paper and the well-known Nelder–Mead algorithm. Also, several numerical examples are carried out to illustrate the features of these models by utilizing the search procedure developed in this paper. Then various models are analytically compared, and identified the best alternative among them based on minimizing total relevant costs.

Introduction

In the recent year, enterprise business becomes complex day after day and environment is look like kaleidoscope. It is important issue that enterprise reduces operating the cost to increase profits. In the inventory management, a manager not only has to take ordering time into consideration, but also has to consider the backorder parameter, which will be a more practical approach. For the reason, the objective of this paper is utilized a net present value approach to devise replenishment policy with allowable shortages in the finite planning horizon by considering a general, time-varying, continuous, deterministic demand function for a product life cycle. Four possible alternatives for the inventory problem are considered in the shortage models according to different policy making.

Numerous research works have been carried out by incorporating linear-increasing demand into inventory models under a variety of circumstances [11]. The literature concerning the replenishment problem for the case of linear-decreasing demand is also well documented [15]. In contrast to the case of linear trend demand, there have been several researchers who have made contributions to the case of non-linear increasing demand for the replenishment problem [31]. Sana [20] dealt with a stochastic economic order quantity model over a finite time horizon and assumed selling price is a random variable that follows a probability density function. Sana [21] dealt with an economic order quantity model for uncertain demand when capacity of own warehouse is limited and the rented warehouse is considered.

In particular, the time value of money represents the interest one might earn on a payment received today until that future date. Buzacott [2] investigated the effects of inflation rate on the EOQ formula and the pricing policies. Chandra and Bahner [3] examined the discounting effects of inflation on the optimal inventory policies of the order-level system and economic lot-size system. Grubbstrom and Kingsman [10] applied the net present value principle to consider the problem of determining the optimal ordering quantities of a purchased item where there are step changes in price.

Over the past 40 years, many scholars have explored the product inventory model, and the use of mathematics or algorithms to define the optimal inventory policy [18, 27]. With the advances in computing, scholars do more to pursue the optimal decision-making solution. The objective function of the total relevant costs considered in our various models is mathematically formulated as a mixed-integer nonlinear programming problem. A complete search procedure is provided to find the optimal solution by employing the properties derived in this paper and the Nelder–Mead algorithm.

The contributions of this paper are: we investigate the optimal number of inventory replenishments, the corresponding optimal inventory replenishment time points and the shortage time points. The objective function of the net present value for the total relevant costs considered in our model is mathematically formulated as a mixed-integer nonlinear programming problem. A complete search procedure is developed to find the optimal solution by employing the properties derived in this paper and the well-known Nelder–Mead algorithm. Also, several numerical examples and the corresponding analyses are carried out to illustrate the features of these models by utilizing the search procedure developed in this paper. Then various models are analytically compared, and identified the best alternative among them based on minimizing total relevant costs. Under this assumption, this paper attempts to answer the following research questions.

• (1) How to formulate the optimal number of replenishments, replenishment time point and shortage time point to obtain the lowest cost when decision maker faced the different demand rate, replenishment cost, holding cost shortage cost, discounting rate of net inflation and fixed planning horizon?

• (2) Under the same cost structure of these four shortage models, which model is the lowest cost model?

• (3) To understand how the different cost parameters influence total cost and decision result, we integrated many kinds of structures and done sensitivity analysis.

The remainder of this paper is organized follows. We introduce related work in “Related Work ” section and present basic assumptions, model environments and mathematical notation in “Model Assumptions and Notation ” section. In “Mathematical Formulation ” section, we formulate the proposed problem as a cost minimization problem, where the number of inventory replenishments, the inventory replenishment time points, and the beginning time points of shortages within the product life cycle are the decision variables. Following the mathematical formulation, in “Solution Procedure” section, a complete search procedure is provided to find the optimal solution by employing the Nelder–Mead algorithm. In “Algorithmic Structure for Nelder–Mead Algorithm” section, several numerical examples are carried out to illustrate the features of our model by utilizing the search procedure developed in “Solution Procedure ” section. Finally, some concluding remarks are made in “Numerical Examples” section.

Related Work

In the past years, several authors had researched the method to solve for the inventory lot-sizing problem with linearly increasing demand, infinite shortage cost, and fixed planning horizon. Yang [33] derived a heuristic decision rule for the replenishment of items over a finite planning horizon during which shortages were allowed. Astanti and Luong [1] developed a replenishment policy for inventory systems with nonlinear increasing demand pattern with allowable shortages and applied a heuristic technique to help determine the operational parameters for the inventory policy. Yang et al. [34] dealt with the problem of determining the optimal replenishment policy with allowable shortages and partial backlogging/lost sales for deteriorating items with stock-dependent demand. Chung and Huang [6] presented a mathematical model on EOQ for constant demand, shortages under permissible delay in payments. Khanra et al. [12] investigated an economic order quantity model over a finite time horizon for an item with a quadratic time dependent demand by considering shortages in inventory under permissible delay in payments. Khanra et al. [13] dealt with a comparison between inventory followed by shortages model and shortages followed by inventory model with variable demand rate and assumed that the stock deteriorates over time which follows a two parameter Weibull distribution. De and Sana [8] investigated an intuitionistic fuzzy economic order quantity inventory model with backlogging. Sana and Goyal [22] dealt with an economic order quantity model for variable lead-time, order dependent purchasing cost, order size, reorder point and lead-time dependent partial backlogging.

Another extension of the inventory model with time-varying demands is to consider the case where shortages are allowed. Goyal et al. [9] proposed a new replenishment policy which was to start each cycle with shortage and after a period of shortages which replenishment should be made and showed that the new type of replenishment policy is superior to the traditional one. It further proposed four heuristic procedures that new replenishment policy. Teng et al. [29] compared various models and established various inventory replenishment policies to solve the problem of determining the timing and number of replenishments. Finally it proposed a simple and computationally efficient optimal method in a recursive fashion. Sarkar [23] dealt with an Economic Order Quantity model for finite replenishment rate where demand and deterioration rate are both time-dependent. Sarkar [24] considered a mathematical model to investigate the retailer’s optimal replenishment policy under permissible delay in payment with stock dependent demand within the Economic Order Quantity framework. Chung and Cárdenas-Barrón [7] studied two inventory models for deterioration under permissible delay in payments. Pal et al. [19] developed an integrated inventory model under three levels of trade credit policy. Sarkar et al. [25] considered an economic production quantity model with rework process at a single-stage manufacturing system with planned backorders. Sarkar et al. [26] proposed study investigates a continuous review inventory model and used an investment function to improve the process quality.

We proceed to review the literature in inventory theories by incorporating the discounting effects of the time value of money. Chung and Lin [5] developed inventory models and derived optimal solutions by employing the discounting cash flow approach for deteriorating items taking account of time value of money over a fixed planning horizon. Sun and Queyranne [28] investigated the general multi-product, multi-stage production and inventory model utilizing the net present value of its total cost as the objective function. Moon et al. [16] developed inventory models for ameliorating/deteriorating items with time-varying demand pattern over a finite planning horizon, taking into account the effects of inflation and time value of money.

In contrast to past research, we explore the demand function follows the product-life-cycle shape for the decision maker to determine the optimal policy with allowable shortages. The objective function of the net present value for the total relevant costs considered in our model is mathematically formulated as a mixed-integer nonlinear programming problem. We will examine the replenishment policies for the various shortage models with product life-cycle shape under inflation and time discounting.

Model Assumptions and Notation

The demand with a product-life-cycle shape can be classified into 4 stages. At the beginning of the planning horizon, the demand increases very slowly. As time goes on, the demand increases very rapidly and eventually reaches a peak. At the last stage, the demand decreases with time and reaches zero at the end of the planning horizon. A key feature differentiates our paper from the previous works is that the demand function follows the shape of a product-life-cycle under inflation and time discounting with allowable shortages. Specifically, we assume that the demand function is a revised version from Beta distribution function. Namely,

$$\begin{aligned} f(t)= & {} \frac{Q}{B(\alpha ,\beta )}t^{\alpha -1}(H-t)^{\beta -1} \end{aligned}$$

(1)

$$\begin{aligned} B(\alpha ,\beta )= & {} \int \limits _0^H {t^{\alpha -1}(H-t)^{\beta -1}\hbox {d}t} \end{aligned}$$

(2)

Beta distribution is a family of continuous probability distributions defined on the interval parametrized by two positive shape parameters, denoted by $\alpha$ and $\beta$, that appear as exponents of the random variable and control the shape of the distribution. We used following notation where $H$ is the planning horizon under consideration, $Q$ is the cumulative quantity of the demand in the planning horizon and $\alpha , \beta$ are the shape parameter and the scale parameter for the revised Beta distribution function. Different values of $\alpha$ and $\beta$ will have different shapes of the demand function. In Fig. 1, we show three different sets of parameters for $\alpha$ and $\beta$ to graphically depict the demand function. If $\alpha = 1$ and $\beta = 2$, the demand is expressed as a linear decreasing function. On the other hand, if $\alpha = 2$ and $\beta = 1$, the demand is expressed as a linear increasing function. If $\alpha = 6$ and $\beta = 3$, the demand function forms up like a product-life-cycle shape.

Fig. 1

Different sets of parameters a, b for the Beta distribution demand function

The mathematical model of the inventory replenishment problem is based on the following assumptions:

• 1. A single item/product is considered in this paper.

• 2. Rate of demand increase or decrease changes following $\alpha$ and $\beta$ with time.

• 3. The planning horizon under consideration is assumed to be finite.

• 4. Lead time is zero.

• 5. Shortages are allowed.

• 6. Inflation and time discounting are allowed.

• 7. Replenishments occur instantaneously at an infinite rate.

• 8. The deteriorating nature of products is not considered.

• 9. Lead-time of replenishment is zero.

• 10. Minimization of total relevant costs is the objective.

Mathematical Formulation

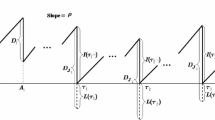
Product inventory to meet customer demand, however, like computer, communication or consumer electronics product life cycle is short than other product. Obsolescent product is easy to stockpile. Therefore, it results in greater inventory cost. Many industries start thinking about the pre-order model for the operation. In this model, when the opportunity cost of failure of sales, loss of customer goodwill, delay cost, or similar costs may not cause a significant impact on the overall cost, enterprise can consider the shortage model. Teng and Leung [30] stated that all four possible alternatives for the inventory problem with in the shortage models. According to different business models, there are four inventory structures. Model 1 starts with an instant replenishment and ends with zero inventories. Model 2 starts with an instant replenishment and ends with shortages. Model 3 starts with shortages and ends with zero inventories. Model 4 starts and ends with shortages. We then analytically compare these four inventory models based on minimizing the total relevant cost for the decision maker of firm which can design inventory structure to decrease the relevant cost.

The $i\hbox {th}$ replenishment is made at time $t_{i}$. The quantity received at $t_{i}$ is used partly to meet the accumulated shortages in the previous cycle from time $s_{i}$ to $t_{i+1}\, (s_{i}< t_{i+1})$ in Model 1 and Model 2. In Model 3 and Model 4, the quantity received at $t_{i}$ is used partly to meet the accumulated shortages in the previous cycle from time $s_{i}$ to $t_{i}\, (s_{i} <t_{i})$. The inventory in Model 1 and Model 2 at $t_{i}$ gradually reduces to zero at $s_{i}\, (t_{i}<s_{i})$ due to demand. In Model 3 and Model 4, the inventory at $t_{i}$ gradually reduces to zero at $s_{i+1}\, (t_{i}<s_{i+1})$ due to demand. Consequently, based on whether the inventory is permitted to start and/or end with shortages, we have four models as shown in Figs. 1, 2, 3, and 4.

Fig. 2

The model starts with an instant replenishment and ends with zero inventories

Fig. 3

The model starts with an instant replenishment and ends with shortages

Fig. 4

The model starts with shortages and ends with zero inventories

The total relevant costs considered in our models include the fixed replenishment cost, the unit purchasing cost, the inventory holding cost, and the inventory shortage cost. The objective of the inventory problem here is to determine the number of replenishments $n$, and the timing of the reorder points $\{t_{i}\}$ and the shortage points $\{s_{i}\}$ in order to minimize the total cost. The mathematical formulation of the objective function for our model can be expressed in Eqs. (3)–(6).

The corresponding total relevant costs of the system for these four models are as follows:

$$\begin{aligned} W_{Model\, 1} (n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} )&=c\left( e^{-Rt_1 }\int \limits _{t_1 }^{s_1 } {f(t)dt} +\sum _{i=1}^{n-2} e^{-Rt_{i+1} }\int \limits _{s_i }^{s_{i+1} } {f(t)dt} + e^{-Rt_n }\int \limits _{s_{n-1} }^H {f(t)dt} \right) \nonumber \\&\quad +\,h\left( {\sum _{i=1}^{n-1} {\int \limits _{t_i }^{s_i } {e^{-Rt}(t-t_i )f(t)dt} } +\int \limits _{t_n }^H {e^{-Rt}(t-t_n )f(t)dt} } \right) \nonumber \\&\quad +\,K\sum _{i=1}^n {e^{-Rt_i }} +s\sum _{i=1}^{n-1} {\int \limits _{s_i }^{t_{i+1} } {e^{-Rt}(t_i -t)f(t)dt} } \end{aligned}$$

(3)

$$\begin{aligned} W_{Model \, 2} (n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} )&=c\left( e^{-Rt_1 }\int \limits _{t_1 }^{s_1 } {f(t)dt} +\sum _{i=1}^{n-2} {e^{-Rt_{i+1} }\int \limits _{s_i }^{s_{i+1} } {f(t)dt} }+\,e^{-RH}\int \limits _{s_{n-1} }^H {f(t)dt} \right) \nonumber \\&\quad +\,h\sum _{i=1}^{n-1} {\int \limits _{t_i }^{s_i } {e^{-Rt}(t-t_i )f(t)dt} } +K\sum _{i=1}^{n-1} {e^{-Rt_i }} +Ke^{-RH}\nonumber \\&\quad +\,s\left( \sum _{i=1}^{n-2} {\int \limits _{s_i }^{t_{i+1} } {e^{-Rt}(t_{i+1} -t)f(t)dt} }+\int \limits _{s_{n-1} }^H {e^{-Rt}(H-t)f(t)dt} \right) \end{aligned}$$

(4)

$$\begin{aligned} W_{Model\, 3} (n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} )&=c\left( {\sum _{i=1}^{n-1} {e^{-Rt_i }\int \limits _{s_i }^{s_{i+1} } {f(t)dt} } +e^{-Rt_n }\int \limits _{s_n }^H {f(t)dt} } \right) \nonumber \\&\quad +\,h\left( {\sum _{i=1}^{n-1} {\int \limits _{t_i }^{s_{i+1} } {e^{-Rt}(t-t_i )f(t)dt} } +\int \limits _{t_n }^H {e^{-Rt}(t-t_n )f(t)dt} } \right) \nonumber \\&\quad +\,K\sum _{i=1}^n {e^{-Rt_i }} +s\sum _{i=1}^n {\int \limits _{s_i }^{t_i } {e^{-Rt}(t_i -t)f(t)dt} } \end{aligned}$$

(5)

$$\begin{aligned} W_{Model \, 4} (n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} )&=c\left( {\sum _{i=1}^{n-1} {e^{-Rt_i }\int \limits _{s_i }^{s_{i+1} } {f(t)dt} } +e^{-RH}\int \limits _{s_n }^H {f(t)dt} } \right) \nonumber \\&\quad +\,h\sum _{i=1}^{n-1} {\int \limits _{t_i }^{s_{i+1} } {e^{-Rt}(t-t_i )f(t)dt} } +K\sum _{i=1}^{n-1} {e^{-Rt_i }} +Ke^{-RH}\nonumber \\&\quad +\,s\left( {\sum _{i=1}^{n-1} {\int \limits _{s_i }^{t_i } {e^{-Rt}(t_i -t)f(t)dt} } +\int \limits _{s_n }^H {e^{-Rt}(H-t)f(t)dt} } \right) \end{aligned}$$

(6)

As a result, the problem now is to determine $n, \{t_{i}\}$ and $\{s_{i}\}$ such that $W_{Model\, j} \left( {n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} } \right) , j = 1, 2, 3$ and 4, are minimized, respectively. The above four equations include the total purchasing costs for the product, the total inventory holding costs, the total replenishment costs and the total shortage costs in the planning horizon. Moreover, we note that the decision variables in four expressions include an integer value $n$, real values of $t_{i}$, and real values of $s_{i}$.

If we take the first derivative of $W_{Model\, j} \left( {n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} } \right) , j = 1$ and 2, with respect to $s_{i}$, then we can have the following result.

$$\begin{aligned} \frac{\partial W_{Model\, j} \left( {n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} } \right) }{\partial s_i }= & {} c\left( {e^{-Rt_i }-e^{-Rt_{i+1} }} \right) f(s_i ) +h\left( {e^{-Rs_i }s_i-e^{-Rs_i }t_i } \right) f(s_i )\nonumber \\&\quad -\,s\left( {e^{-Rs_i }t_{i+1} -e^{-Rs_i }s_i } \right) f(s_i )=0 \end{aligned}$$

(7)

By rearranging Eq. (7), $s_{i}$ can be expressed by $t_{i}$ and $t_{i+1}$, which is shown as in Eq. (8).

$$\begin{aligned} s_i =\frac{e^{-Rs_i }\left( {ht_i +st_{i+1} } \right) -c\left( {e^{-Rt_i }-e^{-Rt_{i+1} }} \right) }{e^{-Rs_i }\left( {h+s} \right) } \end{aligned}$$

(8)

Another, if we take the first derivative of $W_{Model\, j} \left( {n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} } \right) , j = 3$ and 4, with respect to $s_{i}$, then we can have the following result.

$$\begin{aligned} \frac{\partial W_{Model\, j} (n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} )}{\partial s_i }= & {} c\left( {e^{-Rt_{i-1} }-e^{-Rt_i }} \right) f(s_i )+h\left( {e^{-Rs_i }s_i -e^{-Rs_i }t_{i-1} } \right) f(s_i )\nonumber \\&\quad -\,s\left( {e^{-Rs_i }t_i -e^{-Rs_i }s_i } \right) f(s_i )=0 \end{aligned}$$

(9)

By rearranging Eq. (9), $s_{i}$ can be expressed by $t_{i-1}$ and $t_{i}$, which is shown as in Eq. (10).

$$\begin{aligned} s_i =\frac{e^{-Rs_i }\left( {ht_{i-1} +st_i } \right) -c\left( {e^{-Rt_{i-1} }-e^{-Rt_i }} \right) }{e^{-Rs_i }\left( {h+s} \right) } \end{aligned}$$

(10)

Because we can’t obtain the close form, we use the Eq. (5) from Chen et al. [4] to approximate the $s_{i}$ of power in the Eqs. (8) and (10). The approximation is shown as in Eqs. (11) and (12).

$$\begin{aligned} s_i =\frac{e^{-R\frac{\left( {ht_i +st_{i+1} } \right) }{\left( {h+s} \right) }}\left( {ht_i +st_{i+1} } \right) -c\left( {e^{-Rt_i }-e^{-Rt_{i+1} }} \right) }{e^{-R\frac{\left( {ht_i +st_{i+1} } \right) }{\left( {h+s} \right) }}\left( {h+s} \right) } \end{aligned}$$

(11)

and

$$\begin{aligned} s_i =\frac{e^{-R\frac{\left( {ht_{i-1} +st_i } \right) }{\left( {h+s} \right) }}\left( {ht_{i-1} +st_i } \right) -c\left( {e^{-Rt_{i-1} }-e^{-Rt_i }} \right) }{e^{-R\frac{\left( {ht_{i-1} +st_i } \right) }{\left( {h+s} \right) }}\left( {h+s} \right) } \end{aligned}$$

(12)

Moreover, the second partial derivative of $W_{Model\, j} \left( {n,\left\{ {t_i } \right\} ,\left\{ {s_i } \right\} } \right)$ with respect to $s_{i}$ can be easily shown to be positive by evaluating $s_{i}$ at which Eqs. (7) and (9) are satisfied. Therefore, we can substitute $s_{i}$ into the objective function of the four models.

We note that the decision variables in the objective function are the discrete integer variable $n$ and positive real variables of $t_{i}$ for $i = 1, 2, \ldots , n-1$. If we obtain optimal $t_{i}$, then $s_{i}$ of the Model 1 and Model 2 can be obtained by Eq. (11) and the Model 3 and Model 4 can be obtained by Eq. (12) accordingly. Hence, the problem discussed in this paper becomes a cost minimization problem with a mixed-integer multidimensional objective function. It is almost impossible to have analytical closed form solutions for the proposed model. In the following section, we will present a complete search procedure to find out the optimal number of replenishments $n$ and the corresponding optimal replenishment time point $t_{i}$ and the optimal beginning time points of shortage $s_{i}$ for $i = 1, 2, \ldots , n-1$. Specifically, for given any $n$, the Nelder–Mead algorithm will be utilized to solve for the optimal $t_{i}$.

Solution Procedure

In this section, we will first briefly review the Nelder–Mead algorithm. Next, we will show how to improve and apply Nelder–Mead algorithm to find the optimal $t_{i}^{*}$ for any given $n$. Then, the search procedure to find optimal $n^{*}$ is presented. A complete procedure integrates with Nelder–Mead algorithm and search algorithm to determine the optimal $n^{*}$ and $t_{i}^{*}$ is shown as following.

The Nelder–Mead simplex algorithm is the most widely used direct search method for solving the unconstrained optimization problem. The method uses the concept of a simplex, which is a special polytope of N + 1 vertices in N dimensions. Examples of simplexes include a line segment on a line, a triangle on a plane, a tetrahedron in three-dimensional space and so forth. Nelder–Mead algorithm was proposed as a derivative-free method which makes it suitable for problems with non-smooth functions for minimizing a real-valued function $f(\mathbf{x})$ for $\mathbf{x}\in \, \hbox {R}^\mathrm{n}$ and $n$ the dimension. The object of this algorithm is to provide a direct search optimization method to solve the unconstrained optimization problem. The method approximates a local optimum of a problem with N variables when the objective function varies smoothly and is unimodal. For those readers interested in the Nelder–Mead algorithm, please refer to Nelder and Mead [17] for details. The essential concept behind the search procedure of the Nelder–Mead algorithm is that the worst vertex is rejected and replaced by a new better vertex at the each iteration. A new vertex is formed and the search is continued until the vertices converge. The iterations of the Nelder–Mead method consist of the following three steps which are ordering, centroid and transformation. Additionally, iterations of the Nelder–Mead algorithm have an interesting geometrical interpretation. We summarize the search procedure of the Nelder–Mead algorithm as follows.

• 1. Before performing the algorithm, four scalar parameters must be specified to define a complete Nelder–Mead method which are the coefficients of reflection $(\omega )$, expansion $(\theta )$, contraction $(\gamma )$, and shrinkage $(\sigma )$. Lagarias et al. [14] indicates that these four coefficient should satisfy

  $$\begin{aligned} \omega >0,\theta >1,\theta >\omega ,1>\gamma >0,1>\sigma >0 \end{aligned}$$

  (13)

  and the nearly universal choices used in most implementations which should be

  $$\begin{aligned} \omega =1,\theta =2,\gamma =\frac{1}{2},\sigma =\frac{1}{2} \end{aligned}$$

  (14)

• 2. At the beginning of the each iteration, $(n+1)$ vertices are identified and each of which is a point in $\hbox {R}^\mathrm{n}$. Assuming that each iteration begins by ordering and labeling these vertices as $\mathbf{x}^{1}, \mathbf{x}^{2},\ldots , \mathbf{x}^{n+1}$, such that $f(\mathbf{x}^{1})\le f(\mathbf{x}^{2}) \le {\ldots }{\ldots }\le f(\mathbf{x}^{n})\le f(\mathbf{x}^{n+1})$. Define $\overline{\mathbf{x}} =\frac{\sum _\mathrm{{i}=1}^n \mathbf{x}^\mathrm{{i}} }{n}$ is the centroid of $n$ best points (all vertices except for $\mathbf{x}^{n+1})$.

• 3. The result of any iteration is either (1) a single new vertex, which replaces $\mathbf{x}^{n+1}$ in the set of vertices for next iteration, or (2) a shrink, where a set of $n$ new points together with $\mathbf{x}^{1}$ forms up the new set of vertices for next iteration. Specifically, four different operations, which are REFLECTION, EXPANSION, INSIDE CONTRACTION and OUTSIDE CONTRACTION, yields a single new vertex while the SHRINK operation replaces all but one (i.e., $\mathbf{x}^{1})$ vertices to form up the new set of vertices.

• 4. The REFLECTION operation means the worst point $\mathbf{x}^{n+1}$ is reflected through the centroid $\overline{\mathbf{x}}$ by a factor of $\omega$. Based on the result of the REFLCTION operation, EXPANSION operation extends the reflection point along with the reflection path by a factor of $\theta$.

• 5. The OUTSIDE CONTRACTION operation moves the reflection point towards the centroid by a factor of $\gamma$. On the other hand, the INSIDE CONTRACTION operation moves the worse point towards centroid $\overline{\mathbf{x}}$ by a factor of $\gamma$.

• 6. The SHRINK operation causes all vertices but the best point to have their distances to the best point reduced by a factor of $\sigma$. The transformation was used to prevent the algorithm from failing in the failed contraction.

For those five different types of operations in Nelder–Mead algorithm, please refer to Fig. 5 in details for geometric interpretations.

Fig. 5

The model starts and ends with shortages

Algorithmic Structure for Nelder–Mead Algorithm

Figure 6 shows that the process continues and generates a sequence of triangles that converges down on the solution point. The method uses the concept of a simplex, which is a specialv poly-tope of $m+1$ vertices in $m$ dimensions. First, suppose that we have $m$ variables to solve. An iteration of the Nelder–Mead algorithm can be described as follows (Fig. 7).

Fig. 6

Possible outcomes for a step in the Nelder–Mead simplex algorithm for $n$ = 2

Fig. 7

The sequence of triangles converging

• 1. Given $\hbox {parameters}\,\omega , \theta , \gamma , \sigma$ and order the $(m+1)$ vertices to satisfy $f(\mathbf{x}^\mathrm{{1}}) \le f(\mathbf{x}^\mathrm{{2}})\le {\ldots }\le f(\mathbf{x}^{m}) \le f(\mathbf{x}^{m\mathrm {+1}})$. Define $\overline{\mathbf{x}} =\frac{\sum \limits _\mathrm{{i}=1}^m \mathbf{x}^\mathrm{{i}} }{m}$ is the centroid of $m$ best points (all vertices except $\hbox {for}\,\mathbf{x}^{m\mathrm {+1}}$).

• 2. Calculate $\mathbf{x}^\mathrm{{r}}$ from $\mathbf{x}^\mathrm{{r}}=\overline{\mathbf{x}} +\omega (\overline{\mathbf{x}} -\mathbf{x}^{m\mathrm {+1}})=(1+\omega )\times \overline{\mathbf{x}} -\omega \times \mathbf{x}^{m\mathrm {+1}}\,\hbox {and}\, \hbox {evaluate}\,f(\mathbf{x}^\mathrm{{r}})$. If $f(\mathbf{x}^\mathrm{{1}})\le f(\mathbf{x}^\mathrm{{r}})< f(\mathbf{x}^{m})$ then replace $\mathbf{x}^{m\mathrm {+1}}\,\hbox {with}$ the reflection vertex $\mathbf{x}^\mathrm{{r}}\,\hbox {and}$ terminate the iteration.

• 3. If $f(\mathbf{x}^\mathrm{{r}})<f(\mathbf{x}^\mathrm{{1}})$, calculate the expansion $\hbox {vertex}\,\mathbf{x}^\mathrm{{e}}\,\hbox {from}\,\mathbf{x}^\mathrm{{e}}=\overline{\mathbf{x}} +\theta (\mathbf{x}^\mathrm{{r}}-\overline{\mathbf{x}} )=(1+\omega \theta )\overline{\mathbf{x}} -\omega \theta \mathbf{x}^{m\mathrm {+1}}\,\hbox {and evaluate}\,f(\mathbf{x}^\mathrm{{e}})$. If $f(\mathbf{x}^\mathrm{{e}})<f(\mathbf{x}^\mathrm{{r}})$, then replace $\mathbf{x}^{m\mathrm {+1}}\,\hbox {with}$ the expansion vertex $\mathbf{x}^\mathrm{{e}}\,\hbox {and}$ terminate the iteration; otherwise, replace $\mathbf{x}^{m\mathrm {+1}}\,\hbox {with}$ the reflection vertex $\mathbf{x}^\mathrm{{r}}\,\hbox {and}$ terminate the iteration.

• 4. If $f(\mathbf{x}^{m}) \le f(\mathbf{x}^\mathrm{{r}})<f(\mathbf{x}^{m\mathrm {+1}})$, then calculate $\mathbf{x}^\mathrm{{co}}\,\hbox {from}\, \mathbf{x}^\mathrm{{co}}=\overline{\mathbf{x}} +\gamma (\mathbf{x}^\mathrm{{r}}-\overline{\mathbf{x}} )=(1+\omega \gamma )\overline{\mathbf{x}} -\omega \gamma \mathbf{x}^{m+1}\,\hbox {and evaluate}\,f(\mathbf{x}^\mathrm{{co}})$. If $f(\mathbf{x}^\mathrm{{co}})\le f(\mathbf{x}^\mathrm{{r}})$, then replace $\mathbf{x}^{m\mathrm {+1}}\,\hbox {with}$ the outside contraction vertex $\mathbf{x}^\mathrm{{co}}\,\hbox {and}$ terminate the iteration; otherwise, go to Step 6 to perform a shrink.

• 5. On the other hand, if $f(\mathbf{x}^{m\mathrm {+1}})\le f(\mathbf{x}^\mathrm{{r}})$, then calculate $\mathbf{x}^\mathrm{{ci}}\,\hbox {from}\, \mathbf{x}^\mathrm{{ci}}=\overline{\mathbf{x}} -\gamma (\overline{\mathbf{x}} -\mathbf{x}^{m\mathrm {+1}})=(1-\gamma )\overline{\mathbf{x}} +\gamma \mathbf{x}^{m\mathrm {+1}}\,\hbox {and evaluate}\, f(\mathbf{x}^\mathrm{{ci}})$. If $f(\mathbf{x}^\mathrm{{ci}})<f(\mathbf{x}^{m\mathrm {+1}})$, then replace $\mathbf{x}^{m\mathrm {+1}}\,\hbox {with}$ the inside contraction vertex $\mathbf{x}^\mathrm{{ci}}\,\hbox {and}$ terminate the iteration; otherwise, go to Step 6 to perform a shrink.

• 6. Perform a shrink operation. Calculate $\mathbf{v}^\mathrm{{i}}=\mathbf{x}^{1}+\sigma (\mathbf{x}^\mathrm{{i}}-\mathbf{x}^{1})\,\hbox {for}\, \hbox {i}=2, 3,{\ldots },m+1$. Replace $\mathbf{x}^\mathrm{{2}}\,\hbox {by}\,\mathbf{v}^\mathrm{{2}},\mathbf{x}^\mathrm{{3}}\,\hbox {by}\,\mathbf{v}^\mathrm{{3}},{\ldots }, \mathbf{x}^{m}\,\hbox {by}\,\mathbf{v}^{m}\,\hbox {and}\,\mathbf{x}^{m+1}\,\hbox {by}\, \mathbf{v}^{m+1}$. That is, the new set of vertices $\hbox {is}\,\mathbf{x}^{1},\mathbf{v}^\mathrm{{2}},\mathbf{v}^\mathrm{{3}},{\ldots },\mathbf{v}^{m},\mathbf{v}^{m+1}$.

We will show how to apply the Nelder–Mead algorithm to solve our problem. Referring to Eqs. (3)–(6), we seek to minimize the total relevant cost through determining the optimal number of replenishments in the planning horizon $n^{*}$ and the corresponding replenishment time points $t_{i}^{*}\,\hbox {for}$ $i=2,{\ldots }, n^{*}$. Therefore, we can separate our problem into two parts: 1) given any $n$, finding the optimal replenishments in the planning time points $t_{i}^{*}\,\hbox {for}\, i=2,{\ldots }, n, \hbox {and}\, 2)$ finding the optimal number of replenishments in the planning horizon $n^{*}$. We will first describe how to find the optimal replenishment time points $t_{i}^{*}$ by employing the Nelder–Mead algorithm under the condition that the number of replenishments in the planning horizon $n$ is given. Next, we will show search algorithm how to determine the optimal number of replenishments in the planning horizon $n^{*}$. By combining the algorithms, we can have the complete procedure to find the optimal number of replenishments in the planning horizon $n^{*}$ as well as the corresponding optimal replenishment time points $t_{i}^{*}$.

We consider that the number of replenishments is given in the planning horizon and need to identify initial vertices in order to start performing the Nelder–Mead algorithm to find the optimal replenishment time points $t_{i}^{*}$. Since the number of replenishments is $n$ and these two time points $t_{1}$ and $t_{n+1}$ are initialized that $t_{1}$=0 and $t_{n+1}=H$ are given. We need to find $(t_{2}, t_{3},{\ldots }, t_{n})$ such that the total relevant cost is minimized. Because we have ($n-1$) variables to solve, we need to have $n$ vertices initially. The first vertex can be obtained by dividing $H$ equally. Namely,

$$\begin{aligned} \mathbf{t}^{1}=\left( {\frac{H}{n},\frac{2H}{n},\ldots ,\frac{(n-1)H}{n}} \right) \end{aligned}$$

(15)

The second vertex is identical to $\mathbf{t}^{1}\,\hbox {in}$ Eq. (15) except that the first term is multiplied by the factor $(1+\Delta )$, and is shown in Eq. (16). Similarly, the third vertex is identical to $\mathbf{t}^{1}\,\hbox {in}$ equation (15) except that the second term is multiplied by the factor $(1+\Delta )$, and is shown in Eq. (16).

$$\begin{aligned} \mathbf{t}^{2}=\left( {\frac{(1+\Delta )H}{n},\frac{2H}{n},\ldots ,\frac{(n-1)H}{n}} \right) \end{aligned}$$

(16)

The same operations can be performed to obtain the initial $n$ vertices, which are shown in Eq. (17). We note that $\Delta \,\hbox {is}$ usually set to be $\frac{H}{5n}\,\hbox {dynamically}$.

$$\begin{aligned} \left[ {{\begin{array}{ccccc} \mathbf{t}^{1} \\ \mathbf{t}^{2} \\ \vdots \\ \mathbf{t}^{n-1} \\ \mathbf{t}^{n} \\ \end{array} }} \right] =\left[ {{\begin{array}{ccccc} {\frac{H}{n}}&{} {\frac{2H}{n}}&{} \cdots &{} {\frac{(n-2)H}{n}}&{} {\frac{(n-1)H}{n}} \\ {\frac{(1+\Delta )H}{n}}&{} {\frac{2H}{n}}&{} \cdots &{} {\frac{(n-2)H}{n}}&{} {\frac{(n-1)H}{n}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ {\frac{H}{n}}&{} {\frac{2H}{n}}&{} \cdots &{} {\frac{(1+\Delta )(n-2)H}{n}}&{} {\frac{(n-1)H}{n}} \\ {\frac{H}{n}}&{} {\frac{2H}{n}}&{} \cdots &{} {\frac{(n-2)H}{n}}&{} {\frac{(1+\Delta )(n-1)H}{n}} \\ \end{array} }} \right] \end{aligned}$$

(17)

After the initial vertices $\mathbf{t}^{1},\mathbf{t}^{2},{\ldots },\mathbf{t}^{n-1},\mathbf{t}^{n}$ are obtained by Eq. (17), we can perform the Nelder–Mead algorithm to process for our problem. The searching procedure to find the optimal $(t_{1}^{*}, t_{2}^{*},{\ldots }, t_{n-1}^{*})$ is summarized as follows:

Step 0: :

Given the initial vertices $\mathbf{t}^{i}$ for $i$=1,..., $n$, and the relevant parameter $\omega , \theta , \gamma , \sigma$.

Step 1: :

Order the vertices $W(\mathbf{t}^{1}), W(\mathbf{t}^{2}),{\ldots }, W(\mathbf{t}^{n})$, and let $\mathbf{t}^{i}$ be the $i-\hbox {th}\,\hbox {minimum}\,\mathbf{t }\,\hbox {of} W(\mathbf{t})\,\hbox {with}$ sorted $(W(\mathbf{t}^{1}), W(\mathbf{t}^{2}), {\ldots }, W(\mathbf{t}^{n}))$.

Step 2: :

Compute the reflected vertex $\mathbf{t}^\mathrm{r}$ from $\mathbf{t}^\mathrm{r}=\overline{\mathbf{t}} + \omega (\overline{\mathbf{t}} -\mathbf{t}^{n})=(1+\omega )\times \overline{\mathbf{t}} -\omega \times \mathbf{t}^{n}$, where $\overline{\mathbf{t}} =\frac{\sum \limits _{i=1}^{n-1} \mathbf{t}^\mathrm{{i}}}{n-1}\,\hbox {is}$ the centroid of the $n$-1 best points (all vertices except $\hbox {for}\,\mathbf{t}^{n})$. And evaluate $W_{r}=W(\mathbf{t}^{n})$.

Step 3: :

If $W_{r}<W(\mathbf{t}^{1})$, go to Step 4. If $W(\mathbf{t}^{1})\le W_{r}<W(\mathbf{t}^{n-1})$, replace $\mathbf{t}^{n}$ with reflected $\hbox {vertex}\,\mathbf{t}^\mathrm{r}$ and go to Step 8. If $W(\mathbf{t}^{n-1})\le W_{r}<W(\mathbf{t}^{n})$, go to Step 5. If $W(\mathbf{t}^{n})\le W_{r}$, go to Step 6.

Step 4: :

Compute the expansion vertex $\mathbf{t}^\mathrm{e}$ from $\mathbf{t}^\mathrm{{e}}=\overline{\mathbf{t}} +\theta (\mathbf{t}^\mathrm{{r}}-\overline{\mathbf{t}} )=\overline{\mathbf{t}} +\omega \theta (\overline{\mathbf{t}} -\mathbf{t}^{n})=(1+\omega \theta )\times \overline{\mathbf{t}} -\omega \theta \times \mathbf{t}^{n}\,\hbox {and}$ evaluate $W_{e}=W(\mathbf{t}^\mathrm{e})$. If $W_{e}<W_{r}$, replace $\mathbf{t}^{n}$ with expansion vertex $\mathbf{t}^\mathrm{e }\,\hbox {and}$ go to Step 8; otherwise, replace $\mathbf{t}^\mathrm{n}$ with reflected vertex $\mathbf{t}^\mathrm{r}$ and go to Step 8.

Step 5: :

Compute the outside contraction vertex $\mathbf{t}^\mathrm{co}$ from $\mathbf{t}^\mathrm{{co}}=\overline{\mathbf{t}} +\gamma (\mathbf{t}^\mathrm{{r}}-\overline{\mathbf{t}} )=(1+\omega \gamma )\times \overline{\mathbf{t}} -\omega \gamma \times \mathbf{t}^{n}\,\hbox {and evaluate}\, W_{co}=W(\mathbf{t}^\mathrm{co})$. If $W_{co}\le W_{r}$, replace $\mathbf{t}^{n}$ with the outside contraction vertex $\mathbf{t}^\mathrm{co}$ and go to Step 8; otherwise, go to Step 7.

Step 6: :

Compute the inside contraction vertex $\mathbf{t}^\mathrm{ci}$ from $\mathbf{t}^\mathrm{{ci}}=\overline{\mathbf{t}} -\gamma (\overline{\mathbf{t}} -\mathbf{t}^{n})=(1-\gamma )\times \overline{\mathbf{t}} +\gamma \times \mathbf{t}^{n}\,\hbox {and}$ evaluate $W_{ci}=W(\mathbf{t}^\mathrm{ci})$. If $W_{ci}<W(\mathbf{t}^{n})$, replace $\mathbf{t}^{n}$ with the inside contraction vertex $\mathbf{t}^\mathrm{ci}$ and go to Step 8; otherwise, go to Step 7.

Step 7: :

Calculate the $n$ vertices $\mathbf{v}^\mathrm{z}=\mathbf{t}^{1}+\sigma (\mathbf{t}^\mathrm{z}-\mathbf{t}^{1})$, for $z=2, \ldots$, n Replace vertices $\mathbf{t}^{2},{\ldots },\mathbf{t}^{n-1},\mathbf{t}^{n}$ with vertices $\hbox {v}^{2},{\ldots },\mathbf{v}^{n-1},\mathbf{v}^{n}$. Go to Step 8.

Step 8: :

Order the vertices $W(\mathbf{t}^{1}), W(\mathbf{t}^{2}), {\ldots }, W(\mathbf{t}^{n})$, and let $\mathbf{t}^\mathrm{i}$ be the $\hbox {i}^\mathrm{th}\,\hbox {minimum}$ t of $W(\mathbf{t}^{1})\,\hbox {with}$ sorted $(W(\mathbf{t}^{1}), W(\mathbf{t}^{2}), {\ldots }, W(\mathbf{t}^{n}))$. Check if t converges, if yes, then output $t_{i}^{*}\,\hbox {and}\, W(t_{i}^{*})$; otherwise, go to Step 2.

Any fixed $n\,\hbox {which}$ is the number of replenishments is given, we can obtain optimal replenishment time points $t_{i}^{*}$. For notational simplicity, we let

$$\begin{aligned} W(n)=W(n,\left\{ {t_i ^{*}} \right\} ) \end{aligned}$$

(18)

We note that the total relevant cost $W(n)$ is a strictly convex with respect to $n$. If we assume that demand is uniformly distributed in the planning horizon, from EOQ formula, we can obtain the following result

$$\begin{aligned} EOQ=\sqrt{\frac{2KQ}{hH}} \end{aligned}$$

(19)

Therefore, the approximate integer value for $n$ can be expressed as Eq. (20).

$$\begin{aligned} n=\left\lfloor {\sqrt{\frac{QhH}{2K}}} \right\rfloor \end{aligned}$$

(20)

Where $\left\lfloor x \right\rfloor \,\hbox {is}$ the rounded integer of $x$. We note that Eq. (20) is identical to Eq. (18) in Yang et al. [32]. It is apparent that searching $n^{*}\,\hbox {by}$ starting with $n$ as in Eq. (20) is much more efficient than by starting with $n=1$. Therefore, we have the following procedure to find the optimal number of replenishments:

Step 0: :

Choose two initial values of $n$; say $n$ in Eq. (20) and $n-1$. Utilize the Nelder–Mead algorithm to find $\{t_{i}^{*}\}$ and compute $W(n)$ and $W(n-1)$.

Step 1: :

If $W(n)\ge W(n-1)$, then compute $W(n-2), W(n-3)$ until we find $W(k)\le W(k-1)$. Output $n^{*}=k$ and stop.

Step 2: :

If $W(n)<W(n-1)$, then compute $W(n+1), W(n+2)$ until we find $W(k)<W(k+1)$. Output $n^{*}=k$ and stop.

By combining these algorithms, we can have the complete procedure to find out the optimal number of replenishments in the planning horizon $n^{*}$ as well as the corresponding optimal replenishment time points $t_{i}^{*}$.

Numerical Examples

We provide numerical examples to illustrate the features of the proposed model and the corresponding solution procedure. The values of parameters are $H = 1, K = 200, c = 10, h = 5, s = 7, R = 0.05, Q = 5000, \alpha = 3$, and $\beta = 2$. By employing the algorithm presented in the previous section. The optimal solutions can be obtained and shown in Table 1.

Table 1 Computational result for various models of example

In addition, we provide another numerical example that the values of parameters are $H = 1, K = 100, c = 5, h = 3, s = 4, R = 0.1, Q = 3000, \alpha = 6$, and $\beta = 3$. The optimal solutions can be obtained and shown in Table 2.

Table 2 Computational result for various models of example

From the result of Tables 1 and 2, the ranking of the total cost in the different inventory models can be obtained, which indicates Model $3<\hbox {Model}\, 4<\hbox {Model}\, 1<\hbox {Model}\,2$. The results of the above numerical examples show that Model 3 provides the least expensive policy when the demand function follows the shape of a product-life-cycle.

Inventory control is mainly to ensure the inventory maintain at a reasonable level under the condition of business demand. Control the inventory, right time and appropriately order the products to avoid out-stock or shortage. Decrease the inventory space and total inventory cost. Control inventory funds, accelerate cash flow. The problem raised by excessive inventory is the space of the warehouse and storage cost, thereby increasing the product cost. Occupancy large amount of cash flow resulting in sluggish funds. Not only increased the burden of loan interest, but affect the time value and the opportunity income. Resulting the loss of tangible and intangible in products and raw materials. Making the resources of the enterprise idle, and affecting its reasonable configuration and optimization. Cover various contradictions and problems of the production and the whole business process is harmful for improving the management level.

Shortage cost means the loss of product supply interruption, including the loss of material interruption, the loss of delaying shipping, the loss of sale opportunities (also include the loss of goodwill by subjective estimating) and so on. The shortage cost could be the decision related cost depends on whether the enterprise allowed shortage in different situations. If shortage allowed, the shortage cost and inventory amounts negative related. On the contrary, if shortage is not allowed, the shortage cost is zero then the shortage cost is not necessary to be considered.

After entering 21st century, new science discovered and new technology breakthrough. The process of developing science and technology is hard to estimate accurately. Hence, the estimate of future science and technology development is hard to predict many times. Sometimes, the deviation even happened. Therefore, product is no longer produced then sold in technology industry. Production efficiency may not reach the product demand, as in the Product Life Cycle stage, especially in the Growth stage, the product demand is significant growth. So, considering to the inventory policy, shortage gradually became one of the decision policies.

In finance, the net present value (NPV) is defined as the sum of the present values of incoming and outgoing cash flows over a period of time. This paper integrated shortage and net present value. Through different product demand, providing decision maker formulates the stock policy model. Model 3 illustrates that we sell the product from shortage, then reach a time point, and then start to make up for the shortage. This kind of inventory model has often applied to 3C industry. Mostly through new product released, providing consumers pre-order, and producing in this process then make up for the consumers demand. Hence, this optimal decision model is widely used in the reality industry.

Conclusion

Designing effective inventory systems has important ramifications for firms, regulatory bodies, and the market. Numerous research works have been carried out by incorporating linear-increasing demand into inventory models under a variety of circumstances. And several authors had researched the method to solve for the inventory lot-sizing problem with time varying demand, infinite shortage cost, and fixed planning horizon.

In contrast to past research, the contributions of this paper are: (1) author explores the demand function follows the product-life-cycle shape for the decision maker to determine the optimal policy with allowable shortages, (2) author considers the objective function of the net present value for the total relevant costs considered in our model is mathematically formulated as a mixed-integer nonlinear programming problem, (3) author examines the replenishment policies for the various shortage models with product life-cycle shape under inflation and time discounting and (4) author provides a complete search procedure to find the optimal solution by employing the Nelder–Mead algorithm and to determine the optimal number of replenishments, the corresponding optimal replenishment time points, and the shortage beginning time points in the planning horizon for the decision maker.

With the increasing scarcity of resources and changes in the environment in the twenty first century, global awareness and concern about the world’s environment increased and ideas of resources recycling risen. These environmental issues indicated that many governments around the world are confronted with led their legislators to devise laws to encourage this concern. The proposed model can be extended in several ways. For example, an EOQ decision-making retailer is assumed not only to sell the products to public consumers but also to collect those sold used products from public consumers. Also the deteriorating nature of the product and quantity discounts of the unit cost, etc. may be added in this paper for further study.