1 Introduction

With the development of power electronics technology and control technology, permanent magnet synchronous motor (PMSM) has been widely applied in various industrial sectors due to its compact size, high torque/inertia ratio, high torque/weight ratio and absence of rotor loss[1, 2]. PMSM is a complicated high-order, nonlinear system with multiple variables and strong coupling characteristics. Over the last decades, various design methods have been developed.

To get fast four-quadrant operation, good acceleration and smooth starting, the field-oriented control or vector control is widely used in the design of PMSM drives[2], and in this control process, the precise rotor position and speed are needed. The most commonly used control strategy in PMSM is to install an encoder or other kinds of sensors on the rotor shaft to gain the information on rotor speed and position of the motor, but this would increase the system cost and reduce the system reliability[3]. In recent years, to enhance the system performance and reduce the adverse effects of sensors on the system, several algorithms have been suggested to achieve sensorless operation[4–7].

The sensorless control methods can be divided into two categories: signal injection based methods[8, 9] and back electromotive force (back-EMF (electro-motive force)) based methods[10]. The drawbacks of signal injection based methods include the generation of acoustic noise, suffering from secondary saliency and cross-saturation problems. Meanwhile, the methods of back-EMF are unsuitable for low and zero speed, and sensitive to the parameter variations of the PMSM. Extended Kalman filter has been widely used for rotor speed and position estimation in sensorless control of PMSM[11–14]. The filter, including prediction and innovation, requires a lot of recursive computations. However, it is difficult to guarantee convergence of the estimated speed and position[5]. In [15], model reference adaptive system (MRAS) technique has been used for speed estimation in sensorless speed control of PMSM with space vector pulse width modulation. The stable and efficient estimation of rotor speed at low region was guaranteed by simultaneous identification of PMSM. A reduced-order linear Luenberger observer was proposed to obtain the rotor speed of the motor[16]. The rate of convergence for the Luenberger observer was determined through pole assignment. In [17], a speed sensorless control for PMSM with port-controlled Hamiltonian (PCH) model was established. Furthermore, a passive full-order observer was designed to estimate rotor speed.

In order to improve the robustness and accuracy of position and speed estimations, the sliding mode observers were widely used in very recent years[18–20]. The sliding mode observer has better dynamic behavior, robustness against disturbance and high accuracy estimation ability. However, the chattering phenomenon in sliding mode observer is the major drawback. To reduce the chattering, several works based on high order sliding mode techniques have been published to improve the performance[20].

Backstepping control is a new type recursive and systematic design methodology for the feedback control of uncertain nonlinear system, particularly for the system with matched uncertainties[21]. The most appealing point of it is to use the virtual control variable to make the original high order system simple, thus the final outputs can be derived systematically through suitable Lyapunov functions[5].

In this paper, we mainly investigate backstepping sensorless speed controller for permanent magnet synchronous motor based on slide model observer. A sliding model controller, which adopted a saturation function is designed to estimate the back-EMF to reduce the chattering problem. Also, a phase-locked loop is proposed to estimate the rotor velocity and rotor position angle, because it has good tracking performance for the frequency and phase. Meanwhile, the practical stability of the controller-observer scheme is studied via Lyapunov theorem.

The rest of this paper is organized as follows. In Sections 2 and 3, the mathematical model and the backstepping controller for PMSM are presented. The speed and position information of PMSM are estimated by slide model observer in Section 4. Section 5 presents simulation examples to demonstrate the effectiveness of the proposed method. Finally, some conclusions are drawn in Section 6.

2 Mathematic model of PMSM and problem formulation

Assume that magnetic circuit is unsaturated and hysteresis as well as eddy current losses are ignored. The mathematical model of a conventional surface mounted PMSM can be given with above standard assumptions in the d − q frame as[22]

$${{{\rm{d}}{i_d}} \over {{\rm{d}}t}} = - {1 \over {{L_d}}}R{i_d} + p\omega {i_q} + {1 \over {{L_d}}}{u_d}$$
(1)
$${{{\rm{d}}{i_q}} \over {{\rm{d}}t}} = - {1 \over {{L_d}}}R{i_d} + p\omega {i_q} - {{p{\phi _f}} \over L}\omega + {1 \over {{L_d}}}{u_q}$$
(2)
$${{{\rm{d}}\omega} \over {{\rm{d}}t}} = {{3p{\phi _f}} \over {2J}}{i_q} - {B \over J}\omega - {{{T_L}} \over J}$$
(3)

where R is the stator resistance, L d , L q are the d-axes and q-axes stator inductances, u d , u q denote the d-axes and q-axes stator voltages, i d , i q are the d-axes and q-axes stator currents, p is the number of pole pairs of the PMSM, ω is the rotor angular velocity of the motor, φ ƒ is the flux linkage, T L represents the applied load torque disturbance, J is the rotor inertia, and B is the viscous friction coefficient.

To formulate the design problem, according to (1)–(3), the state space model of the PMSM can be rewritten as the following nonlinear system:

((4))

where x(t) is the state vector defined as x. The main control objective is to keep all the signals in the closed loop system bounded and ensure global asymptotic convergence of the speed and current tracking errors to zero.

3 Design of backstepping controller

Backstepping control is an efficient method for nonlinear system. In the backstepping procedure, the first step is to define a virtual control state and then it is forced to become a stabilizing function. Consequently, by appropriately designing the related control input on the basis of Lyapunov stability theory, the error variable can be stabilized. Based on the backstepping design principle, the overall controller design can be established.

3.1 Speed controller design methodology

The controller for the speed state x1 can be designed in three steps.

  • Step 1. To solve speed tracking problem, the state tracking error variable can be defined as

    $${e_1} = x_1^{\ast} - {x_1}$$
    (5)

    where x1* is the reference rotor speed and x1 is the actual rotor speed. For stabilizing the speed component, the speed tracking error dynamics derived from (4) and (5) can be obtained as

    $${\dot e_1} = \dot x_1^{\ast} - {\dot x_1} = {1 \over J}(B{x_1} + {T_L} - {{3p{\phi _f}} \over 2}{x_2}).$$
    (6)

  • Step 2. Choose the following candidate Lyapunov function as

    $${V_1} = {1 \over 2}e_1^2.$$
    (7)

  • Step 3. The time derivative of Lyapunov function (7) can be obtained as

    $${\dot V_1} = {e_1}{\dot e_1} = {{{e_1}} \over J}(B{x_1} + {T_L} - {{3p{\phi _f}} \over 2}{x_2}).$$
    (8)

According to Lyapunov’s stability definition, in order to allow the tracking error to converge to zero, (9) must be satisfied and make \({\dot V_1} < 0\).

$${1 \over J}(B{x_1} + {T_L} - {{3p{\phi _f}} \over 2}{x_2}) = - k{e_1},\;\;k > 0.$$
(9)

Following the backstepping methodology with (9), the virtual control variable input x2 is

$${x_2} = {2 \over {3p{\phi _f}}}(B{x_1} + T + kJ{e_1}).$$
(10)

From (8) and (10), the following equation can be obtained as

$${\dot V_1} = {e_1}{\dot e_1} = - ke_1^2.$$
(11)

Therefore, when (10) is satisfied, the speed error approaches zero. In other word, global asymptotic tracking of speed can be achieved.

PMSM is a complicated high-order, nonlinear system with multiple variables and strong coupling characteristics. Decoupling control is a commonly used method in PMSM control system. The exact thrust force to drive the motor is determined by the q-axis current. Moreover, it is advisable to make the d-axis current x3 be zero for the interest of reduction of power consumption. Since controlling x3 to zero will eliminate the coupling term x1, x3 in (2), the minimal control effort can be expected. In other word, when i d =0, the control scheme is

$$x_2^{\ast} = {2 \over {3p{\phi _f}}}(B{x_1} + T + kJ{e_1})$$
(12)
$$x_3^{\ast} = 0$$
(13)

where x2* is the reference q-axis current and x3* is the reference d-axis current.

3.2 Current controller design methodology

  • Step 1. For the purpose of q-axis current tracking, e2 is selected as the new state variable for current tracking error.

    $${e_2} = x_2^{\ast} - {x_2}.$$
    (14)

    The derivative of e2 is given by

    $$\matrix{{{{\dot e}_2} = \dot x_2^{\ast} - {{\dot x}_2}} \hfill \cr{\quad \quad {{2(B - kJ)} \over {3p{\phi _f}J}}({{3p{\phi _f}} \over 2}{x_2} - B{x_1} - {T_L}) +} \hfill \cr{\quad \quad {{R{x_2}} \over L} + p{x_1}{x_3} - {{{u_q}} \over L} + {{p{\phi _f}} \over L}{x_1}.} \hfill \cr}$$
    (15)

  • Step 2. For a new system based on e1 and e2, we define the second Lyapunov function as

    $${V_2} = {V_1} + {1 \over 2}e_2^2.$$
    (16)

  • Step 3. The time derivative of V2 is given by

    $$\matrix{{{{\dot V}_2} = {{\dot V}_1} + {e_2}{{\dot e}_2} = - ke_1^2 + {e_2}[{{2(B - kJ)} \over {3p{\phi _f}J}}({{3p{\phi _f}} \over 2}{x_2} -} \hfill \cr{\quad B{x_1} - {T_L}) + {{R{x_2}} \over L} + p{x_1}{x_3} - {{{u_q}} \over L} + {{p{\phi _f}} \over L}{x_1}]} \hfill \cr}$$
    (17)

    where u q is the actual control variable. If the stabilizing control law is defined as

    $$\matrix{{{u_q} = L({B \over J}{x_2} - 2{{{B^2}} \over {3p{\phi _f}}}{x_1} - {{2B{T_L}} \over {3p{\phi _f}J}} -} \hfill \cr{\quad {{2{k^2}J} \over {3p{\phi _f}}} + {{R{x_2}} \over L} - p{x_1}{x_3} + {{p{\phi _f}} \over L}{x_1} + {k_1}{e_2})} \hfill \cr}$$
    (18)

    then the following result is obtained as

    $$\matrix{{{{2(B - kJ)} \over {3p{\phi _f}J}}({{3p{\phi _f}} \over 2}{x_2} - B{x_1} - {T_L}) + {{R{x_2}} \over L} +} \hfill \cr{\quad p{x_1}{x_3} - {{{u_q}} \over L} + {{p{\phi _f}} \over L}{x_1} = - {k_1}{e_2},\quad > 0} \hfill \cr}$$
    (19)
    $${\dot V_2} = - k_1^2 - {k_1}e_2^2 < 0.$$
    (20)

Similarly, the d-axis current controller can be designed by the following steps.

  • Step 1. Choose d-axis current tracking error as a new state variable as

    $${e_3} = x_3^{\ast} + {x_3}.$$
    (21)

    Differentiating e3 with respect to time and using the result of (4) give

    $${\dot e_3} = \dot x_3^{\ast} - {\dot x_3} = {R \over L}{x_3} - p{x_1}{x_2} - {{{u_d}} \over L}.$$
    (22)

  • Step 2. For a new system based on e1, e2 and e3, define the third Lyapunov function as

    $${V_3} = {V_2} + {1 \over 2}e_3^2.$$
    (23)

  • Step 3. Differentiating V3 with respect to time yields

    $$\matrix{{{{\dot V}_3} = {{\dot V}_2} + {e_3}{{\dot e}_3} =} \hfill \cr{\quad \quad - ke_1^2 - {k_1}e_2^2 + {e_3}({R \over L}{x_3} - p{x_1}{x_2} - {{{u_d}} \over L}).} \hfill \cr}$$
    (24)

Equation (24) contains the actual control variable u d . If the actual control variable u d is defined as

$${u_d} = R{x_3} - pL{x_1}{x_2} + L{k_2}{e_3},$$
(25)

then \({\dot V_3} < 0\), i.e.,

$${R \over L}{x_3} - p{x_1}{x_2} - {{{u_d}} \over L} = - {k_3}{e_3},\quad {k_3} > 0.$$
(26)

Combining (23) and (25), we obtain

$${\dot V_3} = - k_1^2 - ke_2^2 - ke_3^2.$$
(27)

From (27), it can be seen that the Lyapunov function \({V_3} = ke_1^2 + ke_2^2 + ke_3^2 > 0\) and \({\dot V_3} < 0\), which indicates the tracking error will converge asymptotically to zero. The objective of backstepping control for PMSM is completed.

4 Design of speed observer

The precise rotor position and speed information are essential for implementing back-stepping control of PMSM. However, in industrial applications, because of issues such as space limitations, signal noise and temperature, using sensors to measure the rotor’s position and speed is not suitable. This paper exploits the paradigm of the sliding-mode observer to acquire the rotor position and speed information for PMSM based on backstepping control.

4.1 Sliding-mode observer

The sliding model observer design is modeled in stationary αβ coordinates, (28) shows the transformation matrix between dq-current (i dq ) and αβ-current (i αβ ).

((28))

where θ e denotes the electrical angle of the rotor. Equations (1)–(3) can be expressed as

$${{{\rm{d}}{i_\alpha}} \over {{\rm{d}}t}} = - {1 \over L}R{i_\alpha} + {1 \over L}{i_\alpha} + {1 \over L}{u_\alpha}$$
(29)
$${{{\rm{d}}{i_\beta}} \over {{\rm{d}}t}} = - {1 \over L}R{i_\beta} + {1 \over L}{i_\beta} + {1 \over L}{u_\beta}$$
(30)
$${{{\rm{d}}{i_\omega}} \over {{\rm{d}}t}} = {{3p{\phi _f}} \over {2J}}({i_\beta}\cos {\theta _e} - {i_\alpha}\sin {\theta _e}){B \over J}\omega - {{{T_L}} \over J}.$$
(31)

The electromotive force equation is defined as

$$\left\{{\matrix{{{e_\alpha} = - {\phi _f}{\omega _e}\sin {\theta _e}} \hfill \cr{{e_\beta} = {\phi _f}{\omega _e}\cos {\theta _e}.} \hfill \cr}} \right.$$
(32)

Since the electric time constant is rather small, the stator current response is quicker than the rotation speed. Supposing \(\dot \omega = 0\) in cycle control time, (32) can be rewritten as

$$\left\{{\matrix{{{{\dot e}_\beta} = - {\omega _e}{e_\beta}} \hfill \cr{{{\dot e}_\beta} = {\omega _e}{e_\alpha}.} \hfill \cr}} \right.$$
(33)

From (32), it can be seen that the back-EMF e α and e β are sinusoidal waves, and contain the information of rotor velocity and position information, so the rotor velocity and position can be obtained from the estimated back-EMF. We construct the slide model observer as

$$\left\{{\matrix{{{{{\rm{d}}{s_\alpha}} \over {{\rm{d}}t}} = - {1 \over L}R{s_\alpha} + {1 \over L}{e_\alpha} - {k \over L}{z_\alpha} - {{{k_1}} \over L}{\rm{sat}}({s_\alpha})} \hfill \cr{{{{\rm{d}}{s_\beta}} \over {{\rm{d}}t}} = - {1 \over L}R{s_\beta} + {1 \over L}{e_\beta} - {k \over L}{z_\beta} - {{{k_1}} \over L}{\rm{sat}}({s_\beta})} \hfill \cr}} \right.$$
(34)

where \({s_\alpha} = {\hat i_\alpha} - {i_\alpha},\;{s_\beta} = {\hat i_\beta} - {i_\beta},\;{z_\alpha} = {k_1}\;{\rm{sat}}\;({s_\alpha}) \times {{{\omega _c}} \over {s + {\omega _c}}},\;{z_\alpha} = {k_1}\;{\rm{sat}}\;({s_\beta}) \times {{{\omega _c}} \over {s + {\omega _c}}}\) denotes the feedback coefficient, k1 denotes the slide model coefficient and k1 > 0, ω c denotes the cut-off frequency of one-order, low-pass filter.

The slide model observer reaches the slide model surface within limited time if the inequality is satisfied. The estimated value of the electromotive force can be deduced as

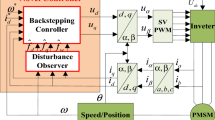
$$\left\{{\matrix{{{{\hat e}_\alpha} = k{z_\alpha} + {k_1}{\rm{sat}}({s_\alpha})} \hfill \cr{{{\hat e}_\beta} = {k_z}\beta + {k_1}{\rm{sat}}({s_\beta}).} \hfill \cr}} \right.$$
(35)

The rotor position of PMSM is related to the phase of the electromotive force. A common method for estimating the actual rotor position is achieved by using arc-tangent function of electromotive force. However, this method leads to disadvantages such as low robustness, low anti-disturbance ability, and inability to adapt to environmental changes. A more serious consequence is the chattering phenomenon caused by parameter variation. In this paper, the phase-locked loop method is used to estimate the speed and position of the rotor, as shown in Fig.1.

Fig. 1
figure 1

Block diagram of phase loop lock (PLL)

Full size image

The deviation between the actual rotator position and the estimated value can be expressed as

$$\Delta e = {\phi _f}{\hat \omega _e}\sin ({\theta _e} - {\hat \theta _e}) = {\hat e_\alpha}\cos {\theta _e} + {\hat e_\beta}\sin {\theta _e}.$$
(36)

In this estimation algorithm, the one-order low-pass filter is used. As a result, phase delay occurs and phase compensation is required. In this paper, phase compensation is achieved by using variable cut-off frequency at a certain reference rotation speed.

$$\Delta {\theta _e} = a\tan ({\omega _e} \times T)$$
(37)

where \(T = {\textstyle{1 \over {M \times {\omega ^{\ast}}}}},\;M\) denotes a constant (normally is 2–5).

4.2 Stability analysis

The designed slide model observer must be stable and satisfy the Lyapunov’s stability condition

$$s\dot s < 0.$$
(38)

Using (34), the previous equation (38) will yield

((39))

, where Δ denotes the boundary-layer thickness of saturation function.

In (39), \( - {R \over L}s_i^2 < 0\) and satisfies (40), therefore the slide model observer is stable.

$${k_1}(1 + {k \over {s + {\omega _c}}}) > \vert{e_i}\vert = {\theta _f}\vert{\omega _e}\vert.$$
(40)

5 Numerical simulation and analysis

Simulation works are carried out on the PMSM to prove the effectiveness of the proposed scheme. The simulations are performed using the Matlab simulink simulation package. In order to validate the control strategies as discussed, digital simulation studies were made using the system described in Fig. 2.

Fig. 2
figure 2

Block diagram of the sensorless PMSM speed control system

Full size image

The stator resistance R is 0.56, the number of pole pairs p is 3, the rotation inertia J is 0.0021 kg/m2, the flux of permanent magnet ϕ ƒ is 0.82 Wb, the inductance L is 0.0153 H, and the viscous damping B is 0.0001.

The initial rotation speed of the motor is 500r/min, and the rotation speed is 100r/min at 0.5 s and 250r/min at 0.8 s, respectively.

The initial load torque of the motor is 5 N·m and the load torque is 10N·m at 0.25 s.

The parameters of the backstepping controller are selected as k = 250, k = 500 and k2 = 150. The parameters of the slide model observer are selected as Δ = 1, k1 = 20, k = 125 and ω c = 40 Hz.

The numerical simulation results are shown in Fig. 3. Fig. 3 (a) indicates the reference rotation speed of the motor and the actual rotation speed. From Fig. 3 (a), it can be seen that the rotation speed of the motor can rapidly track the reference rotation speed with small stability error, fast response and small overshoot. Fig. 3 (b) shows the variation of electromagnetic torque as the load torque changes. From Fig. 3 (b), it can be seen that the motor has fast torque response. Fig. 3 (c) shows the three-phase current of the stator. The current amplitude is proportional to the rotation torque and changes rapidly as the load torque varies. The current frequency is inversely proportional to the rotation speed. Fig. 3 (d) shows the wave of rotor current in d-q frame. In Fig. 3 (d), d-axis current i d is zero, which satisfies the control scheme i d * = 0. In Fig. 3 (e), the magnitude of q-axis current, i q is proportional to the load torque.

Fig. 3
figure 3

Simulink diagram of system

Full size image

Fig. 4 shows the tracking error of actual rotation speed and estimated rotation speed, respectively. It can be seen that there is a relatively larger error when the motor is started. However, after a short while, the slide model observer can accurately and quickly track the rotation speed.

Fig. 4
figure 4

The speed tracking error

Full size image

6 Conclusions

This paper has presented a design method for backstepping control of PMSM based on slide model observer. An efficient backstepping controller was first presented. Then, applying slide model control technique and PLL theory, the slide model observer was designed. The slide model observer is very convenient to be implemented in practice. Finally, numerical examples demonstrated the validity of this approach.