Abstract
In this paper, the problem of controlling chaos in a Sprott E system with distributed delay feedback is considered. By analyzing the associated characteristic transcendental equation, we focus on the local stability and Hopf bifurcation nature of the Sprott E system with distributed delay feedback. Some explicit formulae for determining the stability and the direction of the Hopf bifurcation periodic solutions are derived by using the normal form theory and center manifold theory. Numerical simulations for justifying the theoretical analysis are provided.
Similar content being viewed by others
1 Introduction
Since the pioneering work of Ott et al.[1], the topics of chaos and chaotic control are growing rapidly in many different fields such as ecological system, chemical systems and biological systems, and so forth[2–10]. We all know that chaotic systems have very complicated dynamical nature, which plays an important role in many fields such as secure communications, information processing, high-performance circuit design for telecommunications[11]. Chaos, which often causes irregular behaviors in practical system, is usually undesirable. In many cases, we wish to avoid and eliminate such behaviors. Recently, many schemes such as Ott et al.[1], feedback and non-feedback control[12–17], observer-based control[12], active control[13], adaptive control[18, 19], inverse optimal control[20], evolutionary algorithm[21], etc., have been presented to implement the chaos control. For more related work, one can see [22–26]. In 2012, Wang and Chen[27] reported the very surprising finding of the following new 3D autonomous chaotic Sprott E system with one stable node or stable focus
When a = 0, it is the Sprott E system[28].When a ≠ 0, the stability of the single equilibrium is fundamentally different[29]. Let yz + a = 0, x2 − y = 0, 1 − 4x = 0, we can obtain that system (1) has only one stable equilibrium \(E({x^{\ast}},\;{y^{\ast}},\;{z^{\ast}}) = ({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;16a)\) if a > 0. Interestingly, Wang and Chen[29] found that system (1) can generate chaotic phenomenon which is shown in Fig. 1 (Fig. 1 shows the waveform portraits and the phase portraits of system (1)).
Chaotic attractor of system (1) with a = 0.006. The initial value is (1.5, 1.5, 1.5)
In this paper, we study the stability, and the local Hopf bifurcation nature for system (1). To the best of our knowledge, it is the first try to introduce continuous distributed time-delayed feedback force to control the chaos of the Sprott E system.
The remainder of the paper is organized as follows. In Section 2, we investigate the stability of the equilibrium and the occurrence of local Hopf bifurcations of the Sprott E system with distributed delay feedback. In Section 3, the direction and stability of the local Hopf bifurcation are established. In Section 4, numerical simulations are carried out to show the validity of chaotic control. Some main conclusions are drawn in Section 5.
2 Stability and bifurcation analysis
In this section, we shall study the stability of the equilibrium and the existence of local Hopf bifurcations.
In order to apply feedback control, we add a continuous distributed time delayed force
to the third equation of system (1), then system (1) takes the form
where \(a,\;b > 0,\;\smallint _{- \infty}^0k(s)ds = 1,\;\smallint _{- \infty}^0sk(s)ds < + \infty\). Obviously, system (2) has the equilibrium point \(E({x^{\ast}},\;{y^{\ast}},\;{z^{\ast}}) = ({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;16a)\).
Let \(\bar x(t) = x(t) - {x^{\ast}},\;\bar y(t) = y(t) - {y^{\ast}},\;\bar z(t) = z(t) - {z^{\ast}}\) and still denote \(\bar x(t),\;\bar y(t)\) and \(z(t)\) by x(t), y(t) and z(t), respectively, then (2) becomes
The linearization of (3) near E(x*, y*, z*) is given by
whose characteristic equation appears as
In this paper, we consider the weak kernel case, i.e., k(s) = αe−αs, where α > 0. As to the general gamma kernel case, we can make a similar analysis. We give the initial condition of system (4) as
The characteristic equation (5) with the weak kernel case takes the form
where
In view of the well known Routh-Hurwitz criterion, we can conclude that all the roots of (6) has negative real parts if the following conditions
hold true.
Based on the analysis above, we can easily obtain the following Theorem 1.
-
Theorem 1. The equilibrium E(x*, y*, z*) of system (2) with the weak kernel is locally asymptotically stable if the following conditions are fulfilled:
$$\left\{{\matrix{{\alpha - b + 1 > 0} \hfill \cr{(\alpha - b + 1)(\alpha - b - 2{x^{\ast}}{z^{\ast}} + 4{y^{\ast}}) -} \hfill \cr{\quad [4{y^{\ast}}(1 + \alpha) - 2{x^{\ast}}{z^{\ast}}(\alpha - b)] > 0} \hfill \cr{[4{y^{\ast}}(1 + \alpha) - 2{x^{\ast}}{z^{\ast}}(\alpha - b)] \times} \hfill \cr{\quad \{(\alpha - b + 1)(\alpha - b - 2{x^{\ast}}{z^{\ast}} + 4{y^{\ast}}) -} \hfill \cr{\quad [4{y^{\ast}}(1 + \alpha) - 2{x^{\ast}}{z^{\ast}}(\alpha - b)]\} - 4{y^{\ast}}\alpha {{(\alpha - b + 1)}^2} > 0.} \hfill \cr}} \right.$$Let λ i (i = 1, 2, 3, 4) be the roots of (6), then we have
$$\left\{{\matrix{{{\lambda _1} + {\lambda _2} + {\lambda _3} + {\lambda _4} = - {\theta _1}(\alpha)} \hfill \cr{{\lambda _1}{\lambda _2} + {\lambda _1}{\lambda _3} + {\lambda _1}{\lambda _4} + {\lambda _2}{\lambda _3} + {\lambda _2}{\lambda _4} + {\lambda _3}{\lambda _4} = {\theta _2}(\alpha)} \hfill \cr{{\lambda _1}{\lambda _2}{\lambda _3} + {\lambda _1}{\lambda _2}{\lambda _4} + {\lambda _1}{\lambda _3}{\lambda _4} + {\lambda _2}{\lambda _3}{\lambda _4} = - {\theta _3}(\alpha)} \hfill \cr{{\lambda _1}{\lambda _2}{\lambda _3}{\lambda _4} = {\theta _4}(\alpha).} \hfill \cr}} \right.$$(9)If there exists an α0 ∈ R+ such that D3 (∈0) = 0 and
 , then by the Routh-Hurwitz criterion, there exists a pair of purely imaginary roots, say \({\lambda _1} + {{\bar \lambda}_2} = {\rm{i}}{\omega _0}(\omega \neq 0)\), and the other two roots λ3, X4 satisfy: if X3, X4 are real, then λ3 < 0, λ4 < 0; if λ3, λ4 are complex conjugate, then \({\mathop{\rm Re}\nolimits} \{{\lambda _3}\} = {\mathop{\rm Re}\nolimits} \{{\lambda _4}\} = - {{{\theta _1}(\alpha)} \over 2}\). It is easy to calculate that $$\matrix{{{{{\rm{d}}({\mathop{\rm Re}\nolimits})({\lambda _1}))} \over {{\rm{d}}\alpha}} = - {{{\theta _1}(\alpha)} \over {2[\theta _1^3(\alpha){\theta _3}(\alpha) + {{({\theta _1}(\alpha){\theta _2}(\alpha) - 2{\theta _3}(\alpha))}^2}]}} \times} \hfill \cr{{{\left. {\quad \quad \quad \quad \quad {{{\rm{d}}{D_3}(\alpha)} \over {{\rm{d}}\alpha}}} \right\vert}_{\alpha = {\alpha _0}}}} \hfill \cr}$$(10)
, then by the Routh-Hurwitz criterion, there exists a pair of purely imaginary roots, say \({\lambda _1} + {{\bar \lambda}_2} = {\rm{i}}{\omega _0}(\omega \neq 0)\), and the other two roots λ3, X4 satisfy: if X3, X4 are real, then λ3 < 0, λ4 < 0; if λ3, λ4 are complex conjugate, then \({\mathop{\rm Re}\nolimits} \{{\lambda _3}\} = {\mathop{\rm Re}\nolimits} \{{\lambda _4}\} = - {{{\theta _1}(\alpha)} \over 2}\). It is easy to calculate that $$\matrix{{{{{\rm{d}}({\mathop{\rm Re}\nolimits})({\lambda _1}))} \over {{\rm{d}}\alpha}} = - {{{\theta _1}(\alpha)} \over {2[\theta _1^3(\alpha){\theta _3}(\alpha) + {{({\theta _1}(\alpha){\theta _2}(\alpha) - 2{\theta _3}(\alpha))}^2}]}} \times} \hfill \cr{{{\left. {\quad \quad \quad \quad \quad {{{\rm{d}}{D_3}(\alpha)} \over {{\rm{d}}\alpha}}} \right\vert}_{\alpha = {\alpha _0}}}} \hfill \cr}$$(10)thus the Hopf bifurcation occurs near E(x*,y*,z*) when α passes through α0.
3 Direction and stability of bifurcating periodic solutions
In this section, by using techniques from normal form and center manifold theory[30], we shall investigate the direction, stability, and period of these periodic solutions bifurcating from the equilibrium E(i*, y*, z*). Let μ = α−α0, then system (3) undergoes the Hopf bifurcation at the equilibrium E(x*,y*,z*) for μ = 0, and then ±iω0 are purely imaginary roots of the characteristic equation at the equilibrium E(x*, y*, z*). System (3) can be written as an functional differential equation (FDE) in C = C([−∞, 0]), R3) as
where u(t) = [x(t),y(t),z(t)]T ∈ C and u t (θ) = u(t + θ) = [x(t + θ),y(t + θ), z(t + θ)]T ∈ C, and A and R are given by

and

respectively, where φ(θ) = [φ1 (θ), φ2 (θ), φ3 (θ)]T ∈ C and \({f_1} = {\phi _2}(0){\phi _3}(0),\;{f_2} = \phi _1^2(0)\).
For ψ ∈ C ([0, +∞], (R3)*), define
For φ ∈ C([−∞, 0], R3) and ψ ∈ C([0, +∞], (R3)*), define the bilinear form
where η(θ) = η(θ, 0), the A = A(0) and A* are adjoint operators. By the discussions in Section 2, we know that ±iω0 are eigenvalues of A(0), and they are also eigenvalues of A* corresponding to iω0 and −iω0, respectively. Assume that \(q(\theta) = {(1,\;{a_1},\;{a_2})^T}{{\rm{e}}^{{\rm{i}}{\omega _{\rm{0}}}\theta}}\) is the eigenvector of A(0) corresponding to iω0, then we have A(0) q(0) = iω0q(0), i.e.,

where
We can obtain
where
Assume that \({q^{\ast}}(s) = D{[1,\;a_1^{\ast},\;a_2^{\ast}]^T}{{\rm{e}}^{{\rm{i}}{\omega _{\rm{0}}}s}}(0 \leq s < + \infty)\) is the eigenvector of A*(0) corresponding to −iω0, then we have A*(0)q*(0) = iω0q*(0), i.e.,

where
We can obtain
where
If we choose
then <q*(s),q(θ) ≥ 1 and \(< {q^{\ast}}(s),\;\bar q(\theta) \geq 0\).
Next, we use the same notations as those in Hassard[30] and we first compute the coordinates to describe the center manifold C0 at μ = 0. Let u t be the solution of (11) when μ = 0.
Define
on the center manifold C0, and we have
where
and z and a are local coordinates for center manifold C0 in the direction of q* and \({{\bar q}^{\ast}}\). Noting that W is also real if u t is real, we consider only real solutions. For solutions u t ∈ C0 of (11),
That is
where
Let ƒ0 = [ƒ1, ƒ2]T. Hence, we have
Then, we get
Since there exist unknowns \(W_{20}^{(1)}(0),\;W_{20}^{(3)}(0),\;W_{11}^{(1)}(0),\;W_{11}^{(2)}(0),\;W_{11}^{(3)}(0)\), in g21, we still need to compute them.
It follows from (11) and (14) that

where
Comparing the coefficients, we obtain
For θ ∈ [−∞, 0),
Comparing the coefficients of (21) with (18) gives that
From (19), (22) and the definition of A, we get
Noting that \(q(\theta) = q(0){{\rm{e}}^{{\rm{i}}{\omega _{\rm{0}}}\theta}}\), we have
where \({E_1} = [{E_1}^{(1)},\;{E_1}^{(2)},\;{E_1}^{(3)}] \in {{\bf{R}}^3}\) is a constant vector. Similarly, from (20), (23) and the definition of A, we have
where \({E_2} = [{E_2}^{(1)},\;{E_2}^{(2)},\;{E_2}^{(3)}] \in {{\bf{R}}^3}\) is a constant vector.
In what follows, we shall seek appropriate E1, E2 in (25), (27), respectively. It follows from the definition of A and (22), (23) that
and
where η(θ) = η(0, θ).
Noting that
and substituting (25) and (30) into (28), we have
That is

where
It follows that
where

Similarly, substituting (26) and (31) into (29), we have
That is

It follows that
where

From (25), (27), (32) and (33), we can calculate g21 and derive the following values:
which determine the quantities of bifurcating periodic solutions on the center manifold C0 at the critical value α0, namely, we have the following result.
-
Theorem 2. The periodic solution is supercritical (sub-critical) if μ2 > 0 (μ2 < 0); the bifurcating periodic solutions are orbitally asymptotically stable with asymptotical phase (unstable) if β2 < 0 (β2 > 0); the periods of the bifurcating periodic solutions increase (decrease) if T2 > 0 (T2 < 0).
4 Computer simulations
In this section, we present some numerical results of system (2) to verify the analytical predictions obtained in the previous section. From Section 3, we may determine the direction of a Hopf bifurcation and the stability of the bifurcation periodic solutions. Let us consider the following system:
where k(s)= αe−αs, α > 0. Let yz + 0.006 = 0, x2 − y = 0, 1 − 4x = 0. It is easy to see that system (35) has an equilibrium \({\rm{E}}({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\) and all the conditions indicated in Theorem 2 are satisfied. When τ = 0, the equilibrium \({\rm{E}}({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\) is asymptotically stable. By means of Matlab 7.0, we get α0 ≈ 0.4512. Thus the equilibrium \({\rm{E}}({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\) is stable when α < α0 which is illustrated by the computer simulations (see Fig. 2). When α passes through the critical value a0, the equilibrium \({\rm{E}}({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\) loses its stability and a Hopf bifurcation occurs, i.e., a family of periodic solutions bifurcations from the equilibrium \({\rm{E}}({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\) It follows from the formulae (34) presented in Section 3 that μ2 > 0 and β2 < 0. Then the direction of the Hopf bifurcation is α > α0, and these bifurcating periodic solutions from \({\rm{E}}({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\) around α0 are stable, which are depicted in Fig. 3.
Behavior and phase portraits of system (35) with α = 0.25 < α0 ≈ 0.4512. The equilibrium \({\rm{E}}({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\) is asymptotically stable. The initial value is (1.5, 1.5, 1.5)
Behavior and phase portraits of system (35) with α = 0.55 > α0 ≈ 0.4512. Hopf bifurcation occurs from the equilibrium \(E({\textstyle{1 \over 4}},\;{\textstyle{1 \over {16}}},\;{\textstyle{1 \over 4}},\; - {\textstyle{{12} \over {125}}})\). The initial value is (1.5, 1.5, 1.5)
5 Conclusions
In this paper, a feedback control method is applied to suppress chaotic behavior of a Sprott E system within the chaotic attractor. By adding a continuous distributed time delayed force to the third equation of the Sprott E system, we have made a detailed discussion on the local stability of the equilibrium E(x*, y*, z*) and local Hopf bifurcation of the delayed Sprott E system model. We showed that if some conditions are fulfilled, then the Sprott E system is asymptotically stable for α < α0 and when α passes through α0, a sequence of Hopf bifurcations occur around the equilibrium E(x*, y*, z*), namely, a family of periodic orbits bifurcate from the the equilibrium E(x*, y*, z*), which implies the chaos of this system can be suppress. Some numerical simulations are included to visualize the theoretical findings. Moreover, the control method used in this paper can be applicable to other chaotic systems. We will carry our some related work in near future.
References
E. Ott, C. Grebogi, J. A. York. Controlling chaos. Physical Review Letters, vol. 64, no. 11, pp. 1196–1199, 1990.
X. F. Liao, G. R. Chen, Hopf bifurcations and chaos analysis of chens system with distributed delays. Chaos, Solitons and Fractals, vol. 25, no. 1, pp. 197–220, 2005.
G. Corso, F. B. Rizzato. Hamiltonian bifurcation leading to chaos in a low-energy relativistic wave-particle system. Physica D, vol. 80, no. 3, pp. 296–306, 1995.
A. E. Gohary, A. S. Ruzaiza. Chaos and adaptive control in two prey, one predator system with nonlinear feedback. Chaos, Solitons and Fractals, vol. 34, no. 2, pp. 443–453, 2007.
Y. A. Kuznetsov, S. Rinaldi. Remarks on food chain dynamics. Mathematical Biosciences, vol. 134, no. 1, pp. 1–33, 1996.
M. C. Varriale, A. A. Gomes. A study of a three species food chain. Ecological Modelling, vol. 110, no. 2, pp. 119–133, 1998.
F. Y. Wang, G. P. Pang. Chaos and Hopf bifurcation of a hybrid ratio-dependent three species food chain. Chaos, Solitons & Fractals, vol. 36, no. 5, pp. 1366–1376, 2008.
J. G. Du, T. W. Huang, Z. H. Sheng, H. B. Zhang. A new method to control chaos in an economic system. Applied Mathematics and Computation, vol. 217, no. 6, pp. 2370–2380, 2010.
M. Sadeghpour, H. Salarieh, A. Alasty. Controlling chaos in tapping mode atomic force microscopes using improved minimum entropy control. Applied Mathematical Modelling, vol. 37, no. 3, pp. 1599–1606, 2013.
A. S. Hegazi, E. Ahmed, A. E. Matouk. On chaos control and synchronization of the commensurate fractional order Liu system. Communications in Nonlinear Science and Numerical Simulation, vol. 18, no. 5, pp. 1193–1202, 2013.
G. R. Chen. Controlling Chaos and Bifurcations in Engineering Systems, Boca Raton, FL: CRC Press, 1999.
X. S. Yang, G. R. Chen. Some observer-based criteria for discrete-time generalized chaos synchronization. Chaos, Solitons & Fractals, vol. 13, no. 6, pp. 1303–1308, 2002.
G. R. Chen, X. Dong. On feedback control of chaotic continuous-time systems. IEEE Transactions on Circuits and Systems, vol. 40, no. 9, pp. 591–601, 1993.
M. T. Yassen. Chaos control of Chen chaotic dynamical system. Chaos, Solitons & Fractals, vol. 15, no. 2, pp. 271–283, 2003.
H. N. Agiza. Controlling chaos for the dynamical system of coupled dynamos. Chaos, Solitons & Fractals, vol. 13, no. 2, pp. 341–352, 2002.
H. T. Zhao, Y. P. Lin, Y. X. Dai. Bifurcation analysis and control of chaos for a hybrid ratio-dependent three species food chain. Applied Mathematics and Computation, vol. 218, no. 5, pp. 1533–1546, 2011.
Y. L. Song, J. J. Wei. Bifurcation analysis for Chen’s system with delayed feedback and its application to control of chaos. Chaos, Solitons & Fractals, vol. 22, no. 1, pp. 75–91, 2004.
E. W. Bai, K. E. Lonngren. Sequential synchronization of two Lorenz systems using active control. Chaos, Solitons & Fractals, vol. 11, no. 7, pp. 1041–1044, 2000.
M. T. Yassen. Adaptive control and synchronization of a modified Chua’s circuit system. Applied Mathematics and Computation, vol. 135, no. 1, pp. 113–128, 2001.
T. L. Liao, S. H. Lin. Adaptive control and synchronization of Lorenz system. Journal of the Franklin Institute, vol. 336, no. 6, pp. 925–937, 1999.
H. Richter, K. J. Reinschke, H. Richter, K. J. Reinschke. Optimization of local control of chaos by an evolutionary algorithm. Physica D, vol. 144, no. 3–4, pp. 309–334, 2000.
R. Senkerik, I. Zelinka, D. Davendra, Z. Oplatkova. Utilization of SOMA and differential evolution for robust stabilization of chaotic Logistic equation. Computers & Mathematics with Applications, vol. 60, no. 4, pp. 1026–1037, 2010.
I. Zelinka, M. Chadli, D. Davendra, R. Senkerik, R. Jasek. An investigation on evolutionary reconstruction on continuous chaotic systems. Mathematical and Computer Modelling, vol. 57, no. 1–2, pp. 2–15, 2013.
M. Chadli, I. Zelinka, T. Youssef. Unknown inputs observer design for fuzzy systems with application to chaotic system reconstruction. Computers and Mathematics with Applications, vol. 66, no. 2, pp. 147–154, 2013.
H. A. Yousef, M. Hamdy. Observer-based adaptive fuzzy control for a class of nonlinear time-delay systems. International Journal of Automation and Computing, vol. 10, no. 4, pp. 275–280, 2013.
G. D. Zhao, N. Duan. A continuous state feedback controller design for high-order nonlinear systems with polynomial growth nonlinearities. International Journal of Automation and Computing, vol. 10, no. 4, pp. 267–274, 2013.
X. Wang, G. R. Chen. A chaotic system with only one stable equilibrium. Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 3, pp. 1264–1272, 2012.
J. C. Sprott. Simplest dissipative chaotic flow. Physics Letters A, vol. 228, no. 3–4, pp. 271–274, 1997.
X. Wang, G. R. Chen. Constructing a chaotic system with any number of equilibria. Nonlinear Dynamics, vol. 71, no. 3, pp. 429–436, 2013.
B. Hassard, D. Kazarino, Y. Wan. Theory and Applications of Hopf bifurcation, Cambridge, UK: Cambridge University Press, 1981.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is supported by National Natural Science Foundation of China (Nos. 11261010 and 11101126), Soft Science and Technology Program of Guizhou Province (No. 2011LKC2030), Natural Science and Technology Foundation of Guizhou Province (No. J[2012]2100), Governor Foundation of Guizhou Province (No. [2012]53) and Natural Science and Technology Foundation of Guizhou Province (2014), and Natural Science Innovation Team Project of Guizhou Province (No. [2013]14).
Recommended by Associate Editor Mohammed Chadli
Rights and permissions
About this article
Cite this article
Xu, CJ., Wu, YS. Chaos control and bifurcation behavior for a Sprott E system with distributed delay feedback. Int. J. Autom. Comput. 12, 182–191 (2015). https://doi.org/10.1007/s11633-014-0852-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11633-014-0852-z



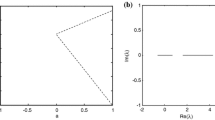

 , then by the Routh-Hurwitz criterion, there exists a pair of purely imaginary roots, say
, then by the Routh-Hurwitz criterion, there exists a pair of purely imaginary roots, say 
