1 Introduction

Fractional calculus [1], which generalizes the conventional calculus theory to non-integer-order systems, has gained too many attentions in the past few decades. The most important reason is that the mathematical knowledge for fractional-order derivatives and integrals has quickly grown and modeling of dynamical systems by fractional calculus techniques has been frequently reported in real-world applications, which includes active magnetic bearing system [2], robot manipulators [3], wind turbine generators [4], big data [5], video streams [6], economics [7] and mechanical systems [8]. In particular, fractional calculus has played a noteworthy role in control theory. In this regard, several fractional controllers, with greater flexibility in improving the robustness and control performance, have attracted considerable interests among scholars [9,10,11,12,13,14,15]. To show the benefits of fractional characterizing of system dynamics, the following illustrative example is given.

Example 1

[8]. Consider a 2D system with initial condition \(x\left( 0\right) =x_{0}\) for \(0<v<1\) as follows.

$$\begin{aligned} \frac{\text {d}}{\text {d}t}x\left( t \right)= & {} vt^{v-1} \end{aligned}$$
(1)
$$\begin{aligned} \frac{{\text {d}^{\alpha }}}{\text {d}t^{{\alpha }}}x\left( t \right)= & {} vt^{v-1},0<\alpha <1 \end{aligned}$$
(2)

in which \(\frac{{\text {d}^{\alpha }}}{{\text {d}t}^{{\alpha }}}\) denotes the Caputo derivative of order \(\alpha \).

By integration, it can be easily computed that \(t^{v}+x_0\) and \(\frac{v\varGamma \left( v \right) t^{v+\alpha -1}}{\varGamma \left( {\alpha +v} \right) }+x_0 \) are the analytical solutions of (1) and (2), respectively. Obviously, although the integer-order system (1) is unstable for any \(v\in \left( 0,1 \right) \), the fractional system (2) is stable as \(0<v\le 1-\alpha \), indicating that this system can utilize extra attractive dynamical attributes over the corresponding integer-order system (1).

Owing to observation in many real-world phenomena, chaos and chaotic behavior have been changed into an interesting topic in recent years. Chaos is an especial case of nonlinear dynamics which displays unusual features such as extraordinary sensitivity to initial conditions and system parameter variations, broad Fourier transform spectra and fractal properties of the motion in the phase space. In general, a chaotic behavior is usually interpreted as locally unbounded oscillations which are globally bounded with a short-time prediction horizon. In this case, control of chaos means forcing the system states to converge a stable equilibrium point or to track a reference command. Although the existence of chaos can be beneficial in some applications (e.g., in oscillators), it may generate harmful oscillations and vibrations in mechanical parts of a system. Such fluctuations should be effectively suppressed. In this regard, control and synchronization of fractional-order chaotic systems have been successfully addressed in the literature and a wide variety of control methods have been proposed. For example, Bigdeli and Ziazi [16] have derived an adaptive active control technique for chaos suppression of uncertain fractional-order chaotic systems. In [17], a prediction-based feedback controller has been given to synchronize two chaotic systems. A passivity-based controller has been developed for fractional-order unified chaotic systems [18]. Sliding mode controllers have been also adopted to realize a stable equilibrium point for fractional chaotic systems [19, 20]. However, many of these approaches have proved an asymptotic stability for the system equilibrium states and they have used multi-input complicated schemes for realizing control of system’s unwanted chaos.

As one of the most popular and successful control methodologies, sliding mode control (SMC) [21] is a version of variable structure control technology which uses switching discontinuous functions to undertake plant parameter fluctuations and external perturbations. The most reason for popularity of SMCs may goes back to the simplicity in practical implementations, low sensitivity to external noises, robustness against system uncertainties and high stability characteristics. The application of SMCs for fractional chaotic systems has been addressed in various papers [22,23,24,25,26]. Chen et al. [27] have introduced a novel class of fractional chaotic systems and have proposed a single-input sliding mode controller for controlling of the system. Since the introduced class of chaotic systems in [27] is general and many fractional chaotic systems belong to that class, considerable attention has been paid to study chaos suppression and synchronization of such systems. Yin et al. [28] have proposed adaptive sliding mode control schemas for chaos control of fractional chaotic systems with unknown parameters. The work [29] has considered the fractional chaotic systems with unknown perturbations and has revisited the problem of sliding mode controller design for robust control of such systems using a one-dimensional control input. A sliding mode control technology for stabilization of the fractional-order systems subjected to model uncertainty and external disturbance has been adopted and realized for chaos control of the fractional-order Chen, Lorenz and a financial system in [30].

Although the above-mentioned sliding mode-based works have attractive features such as simple design technology and good stability property, the convergent to the origin is asymptotic in such sliding modes. In other words, once the system reaches to the sliding surface, even in a finite time, the system trajectories will approach to zero with infinite settling time. Nevertheless, from a practical engineering point of view, it is more valuable to suppress the chaotic behavior of the system in a finite time with quick convergence. Furthermore, accessing finite time stabilization of a dynamical system can provide more accuracy in tracking, quick convergence to the equilibrium and good robustness against external disturbances [31]. To accomplish a finite time stable system, some continuous/discontinuous non-smooth feedback controllers should be provided which result in a non-Lipschitz closed-loop system [31]. Another significant issue in control community is to realize the control of the fractional-order systems by a single-input controller, which can reduce the control effort as well as the complexity of design and implementation. Indeed, the problem of multi-input control schemes is a very critical issue in both theory and practice [32]. However, to the best knowledge of the author, there is no work in the literature for finite time non-smooth control of fractional-order chaotic systems with single input in the presence of mismatched uncertainties to be remained as an open challenge solved in this article.

With this motivation, this paper proposes a new non-smooth switching-type controller, which is based on the sliding mode technique, aiming to stabilize a class of uncertain fractional chaotic systems with external disturbances. In order to improve the convergence speed in both reaching phase and sliding motion, some non-smooth functions are utilized. However, discontinuity in the control law makes undesirable oscillations with finite amplitude and large frequencies which are known as the chattering phenomenon. In practice, it would be more valuable to achieve a fractional SMC with a fast response and low chattering amplitude, too. Hence, this paper removes the discontinuous operator of the control signal by inserting it into a fractional integral leading to a smooth signal without any chattering. Thus, the introduced sliding mode controller is non-smooth in sliding surface and smooth in control law. The outcome will be a finite time stable closed-loop system with no harmful chattering. The proposed control approach will then modified for the systems with parameter variations and external perturbations to produce robustness against unknown fluctuations. Both matched and mismatched uncertainties are considered, and two appropriate sliding mode controllers are derived. In addition to mathematical stability analysis, simulation results are provided to show that the proposed finite time non-smooth-type sliding mode control technology can own a fast response without chattering amplitude.

The reminder of the article is organized as follows. In Sect. 2, mathematical preliminaries of the fractional-order derivatives and integrals as well as fractional stability theorems are presented. Section 3 deals with system description and problem formulation. Control design and stability analysis are involved in Sect. 4. Numerical Simulations are given in Sect. 5. At last, the paper concludes the findings in Sect. 6.

2 Mathematical preliminaries of fractional calculus

In this section, applied definitions of fractional integrals and derivatives as well as their essential properties are given. Then, some necessary fractional-order stability theorems are included.

It is worth to notice that although there are various types of fractional derivatives, the definition of fractional integration is unique as follows.

Definition 1

[1] The fractional integral (or Riemann–Liouville fractional integration) of a function \(f\left( t \right) \) is given by

$$\begin{aligned} { }_{t_0 }I_t^\alpha f\left( t \right) =\frac{1}{\varGamma \left( \alpha \right) }\mathop \int \nolimits _{t_0 }^t \frac{f\left( \tau \right) }{\left( {t-\tau } \right) ^{1-\alpha }}\text {d}\tau \end{aligned}$$
(3)

where \(t_0 \) is the initial time, \(\alpha \in R^{+}\) is the order of integration and \(\varGamma \left( . \right) \) is the Gamma function which is defined as \(\varGamma \left( z \right) =\mathop \int \nolimits _{t_{0}}^\infty t^{z-1}\hbox {e}^{-\hbox {t}}\text {d}t\).

For solving Riemann–Liouville-type fractional differential equations, the fractional-order initial value conditions are required with no apparent practical meanings and even no easy way to measure them. Another definition has been introduced by Caputo to overcome this shortcoming.

Definition 2

[1] The Caputo fractional derivative of a function \(f\left( t \right) \) is defined as follows.

$$\begin{aligned} { }_{t_0 }^{C} D_t^\alpha f\left( t \right)= & {} { }_{t_0 }I^{\left( {m-\alpha } \right) }_t \frac{\text {d}^{m}}{\text {d}t^{m}}f\left( t \right) \nonumber \\= & {} \frac{1}{\varGamma \left( {m-\alpha } \right) }\mathop \int \nolimits _{t_0 }^t \frac{f^{\left( m \right) }\left( \tau \right) }{\left( {t-\tau } \right) ^{\alpha -m+1}}\text {d}\tau \end{aligned}$$
(4)

where \(m-1<\alpha <m\in N\).

Property 1

[1] The following equality holds for \(m=1\).

$$\begin{aligned} { }_{t_0}^{C} D_t^\alpha { }_{t_0 }I_t^\alpha f\left( t \right) ={}_{t_0 }^{RL} D_t^\alpha f\left( t \right) { }_{t_0 }I_t^\alpha f\left( t \right) =f\left( t \right) \end{aligned}$$
(5)

Property 2

[1] For the Caputo definition, the following equality is satisfied for \(m=1\).

$$\begin{aligned} { }_{t_0 }I_t^\alpha { }_{t_0 }^{C} D_t^\alpha f\left( t \right) =f\left( t \right) -f\left( {t_0 } \right) \end{aligned}$$
(6)

In this paper, we use the Caputo definition of the fractional derivatives and for convenience denote it by \(D^{\alpha }\).

Lemma 1

[33] Suppose that \(x=0\) be an equilibrium point for fractional non-autonomous system

$$\begin{aligned} D^{\alpha }x\left( t \right) =f\left( {x,t} \right) \end{aligned}$$
(7)

where \(f\left( {x,t} \right) \) satisfies the Lipschitz condition with Lipschitz constant \(l>0\) and \(\alpha \in \left[ {0,1} \right] \). If there exists a Lyapunov function \(V\left( {t,x\left( t \right) } \right) \) and a class-K functions \(\alpha _i ,i=1,2,3\) satisfying

$$\begin{aligned} \alpha _1 \left( \Vert x \right\| )\le & {} V\left( {t,x}\right) \le \alpha _2 \left( \Vert x \Vert \right) \end{aligned}$$
(8)
$$\begin{aligned} D^{\alpha }V\left( {t,x} \right)\le & {} -\alpha _3 \left( \Vert x \Vert \right) \end{aligned}$$
(9)

then \(x=0\) is the asymptotical stable equilibrium point of the system (7).

Lemma 2

[34] Assume \(f\left( t \right) \in R\) be a continuous and derivable function. Then, for any time instant \(t\ge t_0 \), the following inequality holds.

$$\begin{aligned} \frac{1}{2}{ }_{t_0 }^C D_t^\alpha f^{2}\left( t \right) \le f\left( t \right) { }_{t_0 }^C D_t^\alpha f\left( t \right) \end{aligned}$$
(10)

3 System explanation and problem formulation

In this article, a widely applied class of fractional chaotic systems is taken into account as follows [27].

$$\begin{aligned} \left\{ {{\begin{array}{lll} {D^{q}x=y\cdot f\left( {x,y,z} \right) +z\cdot \varphi \left( {x,y,z} \right) -\alpha x} \\ {D^{q}y=g\left( {x,y,z} \right) -\beta y} \\ {D^{q}z=y\cdot h\left( {x,y,z} \right) -x\cdot \varphi \left( {x,y,z} \right) -\gamma z} \\ \end{array} }} \right. \end{aligned}$$
(11)

where \(q\in \left( {0,1} \right) \) is the fractional order of the differential equations of the system, x, y, \(z\in R^{3}\) are state variables, \(f\left( . \right) \),\(\varphi \left( . \right) \), \(h\left( . \right) \in R^{3}\rightarrow R\) are linear or pseudo-linear functions, \(g\left( . \right) \in R^{3}\rightarrow R\) is a continuous nonlinear function and \(\alpha \), \(\beta \), \(\gamma \in R^{+}\) are some constants.

Remark 1

It is worth noticing that several works in the literature [27, 28] have considered the non-commensurate fractional systems to be controlled. However, since the stability analysis of the control approach of these works has not been performed on the basis of the fractional Lyapunov stability theory of non-commensurate fractional-order systems, their theoretical results are questionable [35, 36].

Remark 2

One can check that the fractional-order model (11) can describe many fractional chaotic systems such as the Lorenz fractional chaotic system and fractional Rucklidge oscillator. Examples of these fractional-order chaotic systems that can be characterized by the model (11) are listed in Table 1.

Table 1 List of several fractional-order chaotic systems described by the model (11)
Full size table

For stabilization and control purposes, one can add the single control input \(u\left( t \right) \) to the second sate equation of the system (11) [27]. Thus, the fractional-order chaotic system (11) can be rewritten as follows.

$$\begin{aligned} \left\{ {{\begin{array}{l} {D^{q}x=y\cdot f\left( {x,y,z} \right) +z\cdot \varphi \left( {x,y,z} \right) -\alpha x} \\ {D^{q}y=g\left( {x,y,z} \right) -\beta y+u\left( t \right) } \\ {D^{q}z=y\cdot h\left( {x,y,z} \right) -x\cdot \varphi \left( {x,y,z} \right) -\gamma z} \\ \end{array}}} \right. \end{aligned}$$
(12)

Remark 3

It should be noted that in all the related previous works the control input has been added into the second state equation of the system. However, in fact, there is no limitation to add the single controller in the other state equations. In this case, both sliding manifold and control input should be modified to satisfy the stability condition of Lyapunov theory. Also, adding the control input \(u\left( t \right) \) into the system dynamics may make the system to be a non-autonomous fractional-order system. Therefore, the stability analysis of the equilibrium point of this system should be carried out using non-autonomous version of the fractional Lyapunov stability theorems [33].

Assumption 2

[27]. Without loss of generality, it is supposed that the functions \(f\left( . \right) \),\(\varphi \left( . \right) \),\(g\left( . \right) \) and \(h\left( . \right) \) can ensure that the fractional chaotic system (12) has a unique solution in \(\left[ {T,\infty } \right) \), \(T>0\) for any known initial condition.

The control objective of this paper is to design a non-smooth sliding mode single-input controller for the system (12) with/without uncertain terms and external disturbances such that the zero equilibrium point of the system is stabled in a given finite time without the chattering phenomenon.

Remark 4

In [37], it has been proved that there is no finite time stable equilibrium point for fractional-order systems. However, the results of [37] are only valid for continuous smooth systems (one can see that in the Theorems 4 and 6 of [37] there is a limitation of continuity for the system function). Actually, this fact exists for integer-order systems, too. However, since our approach is non-smooth and, therefore, the closed-loop system is discontinuous (due to the existence of the sign function in the control input), the results of [37] are not applicable for the non-smooth control design approach introduced in this paper.

4 Main results

In this section, first a non-smooth finite time stable sliding surface is proposed. Then the chatter-free sliding mode control law is derived based on fractional Lyapunov theory. Afterward, the externally distributed system with matched and mismatched parameter variations is considered and the controller is modified to be robust against the unknown uncertain terms.

4.1 Non-smooth sliding surface

According to finite time stability theory [31], non-smooth functions are required to guarantee that the states of the system converge to an equilibrium point within a finite time. Therefore, this paper introduces the following non-smooth sliding surface for the fractional chaotic systems represented by (12).

$$\begin{aligned} s\left( t \right) =D^{q}y+\omega \left( t \right) \end{aligned}$$
(13)

where \(\omega \left( t \right) =x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) \) is a non-smooth function.

The sliding mode condition \(s\left( t \right) =0\) should be satisfied on sliding motion [21]. Thus, one has

$$\begin{aligned} s\left( t \right)= & {} D^{q}y+\omega \left( t \right) =0\rightarrow D^{q}y\nonumber \\= & {} -\left( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) } \right) \nonumber \\ \end{aligned}$$
(14)

Inserting the above equation into the system dynamics (12), one can obtain the sliding mode dynamics as follows.

$$\begin{aligned} \left\{ \!\!{{\begin{array}{lll} {D^{q}x=y\cdot f\left( {x,y,z} \right) +z\cdot \varphi \left( {x,y,z} \right) -\alpha x} \\ {D^{q}y\!=-\left( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) {+}\beta \hbox {sgn}\left( y \right) } \right) } \\ {D^{q}z=y\cdot h\left( {x,y,z} \right) -x\cdot \varphi \left( {x,y,z} \right) -\gamma z} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(15)

Theorem 1

The origin equilibrium point of the fractional-order system (15) is finite time stable.

Proof

Let a Lyapunov function candidate is defined as follows.

$$\begin{aligned} V_1 \left( t \right) =\frac{1}{2}\left( {x^{2}+y^{2}+z^{2}} \right) \end{aligned}$$
(16)

Taking fractional derivative of \(V_1 \left( t \right) \) and using Lemma 2, one has

$$\begin{aligned} D^{q}V_1 \left( t \right) \le xD^{q}x+yD^{q}y+zD^{q}z \end{aligned}$$
(17)

Based on the sliding mode dynamics (15), one can obtain

$$\begin{aligned}&D^{q}V_1 \left( t \right) \le x\left( {y\cdot f\left( {x,y,z} \right) +z\cdot \varphi \left( {x,y,z} \right) -\alpha x} \right) \nonumber \\&\quad +\, y\left( -( x\cdot f\left( {x,y,z} \right) {+}z\cdot h\left( {x,y,z} \right) {+}\beta \hbox {sgn}\left( y \right) ) \right) \nonumber \\&\quad +\, z\left( {y\cdot h\left( {x,y,z} \right) -x\cdot \varphi \left( {x,y,z} \right) -\gamma z} \right) \end{aligned}$$
(18)

Simplifying the above inequality and using \(y\hbox {sgn}\left( y \right) =\left| y \right| \), we have

$$\begin{aligned} D^{q}V_1 \left( t \right) \le -\alpha x^{2}-\beta \left| y \right| -\gamma z^{2}\le 0 \end{aligned}$$
(19)

Since, referencing to Lemma 1, one concludes that the states of the sliding mode dynamics (15) converge the origin asymptotically.

The final step of the proof procedure is to show the convergence happens in finite time. To reach this end, define

$$\begin{aligned} V_{1s} \left( t \right) =0.5y^{2}\le V_1 \left( t \right) \end{aligned}$$
(20)

Thus, inequality (19) can be rewritten in the following form.

$$\begin{aligned} D^{q}V_1 \left( t \right)\le & {} -\alpha x^{2}-\beta \left| y \right| +-\gamma z^{2}\le -\beta \left| y \right| \nonumber \\= & {} -\frac{\beta }{\sqrt{0.5}}\left( {V_{1s} \left( t \right) } \right) ^{0.5} \end{aligned}$$
(21)

On the other hand, there exists a constant \(\eta >0\) such that [38]

$$\begin{aligned} \eta \left( {V_1 \left( t \right) } \right) ^{0.5}\le \left( {V_{1s} \left( t \right) } \right) ^{0.5} \end{aligned}$$
(22)

Using (21) and applying square root operator and then multiplying \(-\frac{\beta }{\sqrt{0.5}}\) to both sides of the above inequality, one can obtain

$$\begin{aligned} D^{q}V_1 \left( t \right) \le -\frac{\beta }{\sqrt{0.5}}\left( {V_{1s} \left( t \right) } \right) ^{0.5}\le -\frac{\beta \eta }{\sqrt{0.5}}\left( {V_1 \left( t \right) } \right) ^{0.5}\nonumber \\ \end{aligned}$$
(23)

Using Property 2 and integrating both sides of the above inequality from 0 to t, one has

$$\begin{aligned}&V_1 \left( t \right) -V_1 \left( 0 \right) \nonumber \\&\quad \le -\frac{\beta \eta }{\sqrt{0.5}\varGamma \left( q \right) }\mathop \int \nolimits _0^t \left( {V_1 \left( \tau \right) } \right) ^{0.5}\left( {t-\tau } \right) ^{q-1}\text {d}\tau \end{aligned}$$
(24)

Letting \(V_1 \left( t \right) -V_1 \left( 0 \right) =\mathop \int \limits _0^t {{\dot{V}}_1}(\tau )\text {d}\tau \), we get

$$\begin{aligned} \mathop \int \nolimits _0^t \frac{{{{\dot{V}}_1}\left( \tau \right) }}{{{{\left( {{V_1}\left( \tau \right) } \right) }^{0.5}}}}\text {d}\tau \le - \frac{{\beta \eta }}{{\sqrt{0.5}\varGamma \mathrm{{\varGamma }}\left( q \right) }}\mathop \int \nolimits _0^t {\left( {t - \tau } \right) ^{q - 1}}\text {d}\tau \end{aligned}$$
(25)

Solving the integration, one obtains

$$\begin{aligned} 2\left( {V_1 \left( t \right) } \right) ^{0.5}\left| {{\begin{array}{l} t \\ 0 \\ \end{array} }} \right. \le -\frac{\beta \eta t^{q}}{\sqrt{0.5}\varGamma \left( {q+1} \right) } \end{aligned}$$
(26)

Now, if we set \(V_1 \left( t \right) \equiv 0\) for \(\infty \ge t\ge T_1 \), then it can be concluded that

$$\begin{aligned} T_1 \le \root q \of {\frac{2\sqrt{0.5}\varGamma \left( {q+1} \right) \left( {V_1 \left( 0 \right) } \right) ^{0.5}}{\beta \eta }} \end{aligned}$$
(27)

Therefore, the origin of the sliding mode dynamics (15) is finite time stable. Thus, the proof is completed. \(\square \)

4.2 Sliding control law

As the second part of a sliding mode control scheme, the proper control law should be provided to force system states to reach the sliding manifold and stay on it forever. The control law includes two components: (a) equivalent control and (b) switching control [21]. The equivalent control is responsible for dealing with nonlinear dynamics of the system and for reaching the system states to the sliding manifold. It is computable from some sliding motion rules [21]. In this paper, the equivalent control is obtained using the following condition.

$$\begin{aligned} s\left( t \right) =0 \end{aligned}$$
(28)

Using \(s\left( t \right) \) in Eq. (13), one has

$$\begin{aligned} s\left( t \right)= & {} D^{q}y+\left( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) }\right. \nonumber \\&\left. {+\beta \hbox {sgn}\left( y \right) } \right) =0 \end{aligned}$$
(29)

Inserting \(D^{q}y\) from the system dynamics (12), we have

$$\begin{aligned}&s\left( t \right) =g\left( {x,y,z} \right) -\beta y+u\left( t \right) +\left( x\cdot f\left( {x,y,z} \right) \right. \nonumber \\&\left. \quad +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) \right) =0 \end{aligned}$$
(30)

Thus, the equivalent control is computed as follows.

$$\begin{aligned} u_{eq} \left( t \right)= & {} -(g\left( {x,y,z} \right) -\beta y+x\cdot f\left( {x,y,z} \right) \nonumber \\&+z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) ) \end{aligned}$$
(31)

However, to avoid the chattering, the term \(\beta \hbox {sgn}\left( y \right) \) is removed from the equivalent control (31). Therefore, the final \(u_{eq} \left( t \right) \) is proposed as below.

$$\begin{aligned}&u_{eq} \left( t \right) {=}-(g\left( {x,y,z} \right) \nonumber \\&\quad -\beta y+x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) ) \end{aligned}$$
(32)

The switching control is in charge to keep the system states on the sliding manifold and tackle the system uncertainties and external noises [21]. The most important drawback of the sliding mode control rule is the existence of the sign function in the switching control. The sign function is a discontinuous hard switcher which forces the system states to oscillate with high frequency and finite amplitude. This phenomenon is known as chattering. Due to limitations in switching devices and delays of physical systems, the chattering will result in low control accuracy, high heat losses in power electronic circuits and bruising of moving mechanical parts [19]. In this paper, to prevent the chattering, an integral-type switching control law is proposed such that the discontinuous function is transferred into that providing a smooth control signal.

$$\begin{aligned} u_{sw} \left( t \right) =-kD^{-q}\left( {\hbox {sgn}\left( s \right) } \right) \end{aligned}$$
(33)

where \(k>0\) is a constant representing the switching gain.

According to Eqs. (32) and (33), the final control signal is proposed as follows.

$$\begin{aligned} u\left( t \right)= & {} -(g\left( {x,y,z} \right) -\beta y+x\cdot f\left( {x,y,z} \right) \nonumber \\&+z\cdot h\left( {x,y,z} \right) +kD^{-q}\left( {\hbox {sgn}\left( s \right) } \right) ) \end{aligned}$$
(34)

Theorem 2

Assume that the chaotic fractional-order system (12) is controlled by the control signal (34). The states of this system will attain the sliding surface \(s\left( t \right) =0\) in finite time.

Proof

Choosing a Lyapunov function candidate in the form of \(V_2 \left( t \right) =\frac{1}{2}s^{2}\) and taking fractional derivative of it, one can obtain

$$\begin{aligned} D^{q}V_2 \left( t \right) \le sD^{q}s \end{aligned}$$
(35)

Replacing \(s\left( t \right) \) by Eq. (30), one gets

$$\begin{aligned}&D^{q}V_2 \left( t \right) \le sD^{q}\left[ {g\left( {x,y,z} \right) -\beta y+u\left( t \right) }\right. \nonumber \\&\left. +\big ( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) } \right] \end{aligned}$$
(36)

Inserting \(u\left( t \right) \) from (34) into the above inequality, we have

$$\begin{aligned} D^{q}V_2 \left( t \right)\le & {} sD^{q}\left[ {g\left( {x,y,z} \right) }\right. \nonumber \\&-\,\beta y{-}\left( {g\left( {x,y,z} \right) -\beta y+x\cdot f\left( {x,y,z} \right) }\right. \nonumber \\&\left. +\,z\cdot h\left( {x,y,z} \right) +kD^{-q}\left( {\hbox {sgn}\left( s \right) } \right) \right) \nonumber \\&\left. +\,\left( {x{\cdot } f\left( {x,y,z}\right) {+}z\cdot h\left( {x,y,z}\right) {+}\beta \hbox {sgn}\left( y \right) } \right) \right] \nonumber \\ \end{aligned}$$
(37)

Simplifying the above inequality, we have

$$\begin{aligned} D^{q}V_2 \left( t \right) \le -sD^{q}\left[ {kD^{-q}\left( {\hbox {sgn}\left( s \right) } \right) -\beta \hbox {sgn}\left( y \right) } \right] \end{aligned}$$
(38)

Since \(\beta \hbox {sgn}\left( y \right) \) is a constant, using the definition of the Caputo fractional derivative one can conclude that \(D^{q}\left[ {\beta \hbox {sgn}\left( y \right) } \right] =0\), this yields

$$\begin{aligned} D^{q}V_2 \left( t \right) \le -sD^{q}\left[ {kD^{-q}\left( {\hbox {sgn}\left( s \right) } \right) } \right] \end{aligned}$$
(39)

Subsequently, according to property 1, one has

$$\begin{aligned} D^{q}V_2 \left( t \right) \le -k\left| s \right| \le 0 \end{aligned}$$
(40)

Thus, referencing to Lemma 1, one concludes that the states of the sliding motion happens asymptotically. \(\square \)

Now it is time to show that the sliding motion occurs in finite time. Using Property 2 and integrating both sides of the above inequality from 0 to \(t_r \), one has

$$\begin{aligned}&V_2 \left( {t_r } \right) -V_2 \left( 0 \right) \nonumber \\&\quad \le -\frac{k}{\sqrt{0.5}\varGamma \left( q \right) }\mathop \int \limits _0^t \left( {V_2 \left( \tau \right) } \right) ^{0.5}\left( {t-\tau } \right) ^{q-1}\text {d}\tau \end{aligned}$$
(41)

Letting \(V_2 \left( {t_r } \right) -V_2 \left( 0 \right) =\mathop \int \limits _0^{t_r } {{\dot{V}}_2}\left( \tau \right) \text {d}\tau \), we get

$$\begin{aligned} \mathop \int \limits _0^{{t_r}} \frac{{{{\dot{V}}_2}\left( \tau \right) }}{{{{\left( {{V_2}\left( \tau \right) } \right) }^{0.5}}}}\text {d}\tau \le - \frac{k}{{\sqrt{0.5}\varGamma \mathrm{{\varGamma }}\left( q \right) }}\mathop \int \limits _0^{{t_r}} {\left( {t - \tau } \right) ^{q - 1}}\text {d}\tau \end{aligned}$$
(42)

Solving the integration, one obtains

$$\begin{aligned} 2\left( {V_2 \left( t \right) } \right) ^{0.5}\left| {{\begin{array}{l} {t_r } \\ 0 \\ \end{array} }} \right. \le -\frac{kt_r^q }{\sqrt{0.5}\varGamma \left( {q+1} \right) } \end{aligned}$$
(43)

Now, if we set \(V\left( {t_r } \right) \equiv 0\) for \(\infty \ge t\ge T_2 \), then it can be concluded that

$$\begin{aligned} T_2 \le \root q \of {\frac{2\sqrt{0.5}\varGamma \left( {q+1} \right) \left( {V_2 \left( 0 \right) } \right) ^{0.5}}{k}} \end{aligned}$$
(44)

Therefore, the states of the system (12) will attain the sliding surface \(s\left( t \right) =0\) in a given finite time. This completes the proof.

4.3 Control for matched disturbed uncertain system

It is well known that in practice most of the physical chaotic systems are inherently with unknown nonlinearities. Besides, in real-world applications, due to modeling errors, structural variations of the system, environment noises, mutual interfere between the system components, etc, the dynamics of the chaotic systems are inevitably disturbed by unknown variations and external disturbances. Whereas due to the high sensitivity of the chaotic systems to the variations of any parameters of the system the presence of the unknown uncertainties and external disturbances can lead to unpredictable behaviors in chaotic systems and even destabilize the controlled chaotic system. Therefore, the proposed control law is modified to show robust behavior against the above-mentioned fluctuations. First, matched unknown uncertain terms as well as external disturbances are added to the system dynamics (12) as follows.

$$\begin{aligned} \left\{ \!\!{{\begin{array}{lll} {D^{q}x=y\cdot f\left( {x,y,z} \right) +z\cdot \varphi \left( {x,y,z} \right) -\alpha x} \\ {D^{q}y=g\left( {x,y,z} \right) -\beta y+\Delta \left( {x,y,z} \right) +\text {d}\left( t \right) +u\left( t \right) } \\ {D^{q}z=y\cdot h\left( {x,y,z} \right) -x\cdot \varphi \left( {x,y,z} \right) -\gamma z} \\ \end{array} }} \right. \end{aligned}$$
(45)

where \(\Delta \left( {x,y,z} \right) \) is an unknown system variation and \(\text {d}\left( t \right) \) represents unknown external perturbations.

Assumption 3

The boundedness attribute of the chaotic systems states as well as the existence of chaotic attractors [39] implies that the system uncertainties and external disturbances should be bounded. Thus, there are suitable positive constants \(\mu \), \(\rho \) and \(\sigma \) such that the following inequalities are satisfied.

$$\begin{aligned} \left| {D^{q}\Delta \left( {x,y,z} \right) } \right|\le & {} \mu \Vert \left( {x,y,z} \right) \Vert +\rho \nonumber \\ \left| {D^{q}\text {d}\left( t \right) } \right|\le & {} \theta \end{aligned}$$
(46)

where \(\Vert \left( {x,y,z} \right) \Vert =\sqrt{x^{2}+y^{2}+z^{2}}\).

Here the previous non-smooth sliding surface (13) is adopted and the overall robust control law is designed as follows.

$$\begin{aligned}&u\left( t \right) =-(g\left( {x,y,z} \right) -\beta y+x\cdot f\left( {x,y,z} \right) \nonumber \\&\quad +\,z\cdot h\left( {x,y,z} \right) +D^{-q}\left[ {\left( {{\mu }\Vert \left( {x,y,z} \right) \Vert +K} \right) \hbox {sgn}\left( s \right) } \right] \nonumber \\ \end{aligned}$$
(47)

where \(K>{\rho }+{\theta }\) is a positive constant.

It should be noted that it is assumed that the amounts of \(\mu \), \(\rho \) and \(\theta \) are known in advance. In fact, although there is little knowledge about the exact values of the uncertainties and external disturbances, it is reasonable to assume that their bounds are known in practice. Indeed, one can select a large enough K to satisfy the condition \(K>\rho +\theta \)

Theorem 3

Consider the uncertain chaotic fractional-order system (45) is controlled by the control signal (47). The states of this system will reach the sliding surface \(s\left( t \right) =0\) in finite time.

Proof

Selecting a Lyapunov function candidate in the form of \(V_3 \left( t \right) =\frac{1}{2}s^{2}\) and taking fractional derivative of it, one can obtain

$$\begin{aligned} D^{q}V_3 \left( t \right) \le sD^{q}s \end{aligned}$$
(48)

Based on Lemma 2 and using the system dynamics (45) and the sliding surface (13), one gets

$$\begin{aligned} D^{q}V_3 \left( t \right)\le & {} sD^{q}\left[ {g\left( {x,y,z} \right) -\beta {y}+\Delta \left( {x,y,z} \right) }\right. \nonumber \\&+\hbox {d}\left( t \right) +u\left( t \right) +\left( {x\cdot f\left( {x,y,z} \right) }\right. \nonumber \\&\left. \left. {+z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) } \right) \right] \end{aligned}$$
(49)

It is clear that

$$\begin{aligned}&D^{q}V_3 \left( t \right) \le sD^{q}\left[ {g\left( {x,y,z} \right) -\beta y+u\left( t \right) }\right. \nonumber \\&\quad \left. +\left( x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) \right) \right] \nonumber \\&\quad +\left| s \right| \left( {\left| {D^{q}\Delta \left( {x,y,z} \right) } \right| } +\left| {D^{q}\text {d}\left( t \right) } \right| \right) \end{aligned}$$
(50)

Applying Assumption 3, one has

$$\begin{aligned}&D^{q}V_3 \left( t \right) \le sD^{q}\left[ {g\left( {x,y,z} \right) -\beta {y}+u\left( t \right) }\right. \nonumber \\&\left. +\left( x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) \right) \right] \nonumber \\&+\left| s \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert +\rho +\theta } \right) \end{aligned}$$
(51)

Inserting \(u\left( t \right) \) from (47) into the above inequality, we have

$$\begin{aligned} D^{q}V_3 \left( t \right)\le & {} sD^{q}\left[ {g\left( {x,y,z} \right) -\beta y-\left( {g\left( {x,y,z} \right) }\right. }\right. \nonumber \\&-\beta y+x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) \nonumber \\&\left. +D^{-q}\left[ {\left( {{\mu }\Vert \left( {x,y,z} \right) \Vert +K} \right) \hbox {sgn}\left( s \right) } \right] \right) \nonumber \\&+\left( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) }\right. \nonumber \\&\left. \left. +\beta \hbox {sgn}\left( y \right) \right) \right] {+}\left| s \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert {+}\rho {+}\theta } \right) \nonumber \\ \end{aligned}$$
(52)

Simplifying the above inequality, we have

$$\begin{aligned}&D^{q}V_3 \left( t \right) {\le } -sD^{q}\left[ D^{-q}\left[ {\left( {\mu \Vert \left( {x,y,z} \right) \Vert {+}K} \right) \hbox {sgn}\left( s \right) } \right] \right. \nonumber \\&\quad \left. -\beta \hbox {sgn}\left( y \right) \right] +\left| s \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert +\rho +\theta } \right) \end{aligned}$$
(53)

\(\square \)

On the basis of Property 1 and \(D^{q}\left[ {\beta \hbox {sgn}\left( y \right) } \right] =0\), one obtains

$$\begin{aligned} D^{q}V_3 \left( t \right)\le & {} -\left( {K+\mu \Vert \left( {x,y,z} \right) \Vert }\right) \left| s \right| \nonumber \\&+\left| s \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert +\rho +\sigma } \right) \nonumber \\\le & {} -\left( {K-{\rho }-{\theta }} \right) \left| s \right| \le 0 \end{aligned}$$
(54)

Thus, using Lemma 1, one concludes that the states of the uncertain system (45) will reach the sliding surface (13) asymptotically. Moreover, a similar approach given in Eqs. (41)–(44) can be utilized to show that the sliding motion occurs in finite time \(T_3 \le \root q \of {\frac{2\sqrt{0.5}\varGamma \left( {q+1} \right) \left( {V_3 \left( 0 \right) } \right) ^{0.5}}{K-\rho -\theta }}\). Hence, the proof is completed.

4.4 Control for mismatched uncertain system

As appeared in Eqs. (15) and (45), the considered uncertainty terms are matched types. However, one can assume that there are some special mismatched uncertainties in the system dynamics. In this regard, the system dynamics (45) is modified as follows.

$$\begin{aligned} \left\{ \!\! {{\begin{array}{lll} D^{q}x=y\cdot f\left( {x,y,z} \right) +z\cdot \varphi \left( {x,y,z} \right) \\ \quad -\alpha x+\Delta _x \left( {x,y,z,t} \right) \\ D^{q}y=g\left( {x,y,z} \right) -\beta y+\Delta \left( {x,y,z} \right) \\ \quad +\text {d}\left( t \right) +\vartheta \left( t \right) \\ D^{q}z=y\cdot h\left( {x,y,z} \right) -x\cdot \varphi \left( {x,y,z} \right) -\gamma z\\ \quad +\Delta _z \left( {x,y,z,t} \right) \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(55)

where \(\vartheta \left( t \right) \in R\) is the control signal and \(\Delta _x \left( {x,y,z,t} \right) \) and \(\Delta _z \left( {x,y,z,t} \right) \) represent the mismatched uncertain terms of the system in which they are assumed to be bounded by two positive constants \(\delta _x \) and \(\delta _z \) as below.

$$\begin{aligned} \left| {\Delta _x \left( {x,y,z,t} \right) } \right| \le \delta _x \left| y \right| , \quad \left| {\Delta _z \left( {x,y,z,t} \right) } \right| \le \delta _z \left| y \right| \end{aligned}$$
(56)

To handle the mismatched uncertainties, only the sliding surface (13) should be revised first. Accordingly, the sliding manifold (13) is modified as follows.

$$\begin{aligned} {\upsigma }\left( t \right) =D^{q}y+\pi \left( t \right) \end{aligned}$$
(57)

where \(\pi \left( t \right) =x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\left( {\beta +\delta _x \left| x \right| +\delta _z \left| z \right| } \right) \hbox {sgn}\left( y \right) \) is a non-smooth function.

Then, using \({\upsigma }\left( t \right) =0\) the sliding mode dynamics becomes

$$\begin{aligned} \left\{ \!\! {{\begin{array}{lll} D^{q}x=y\cdot f\left( {x,y,z} \right) +z\cdot \varphi \left( {x,y,z} \right) -\alpha x\\ \quad +\Delta _x \left( {x,y,z,t} \right) \\ D^{q}y=-\left( x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) \right. \\ \quad \left. +\left( {\beta +\delta _x \left| x \right| +\delta _z \left| z \right| } \right) \hbox {sgn}\left( y \right) \right) \\ D^{q}z=y\cdot h\left( {x,y,z} \right) -x\cdot \varphi \left( {x,y,z} \right) \\ \quad -\gamma z+\Delta _z \left( {x,y,z,t} \right) \\ \end{array} }} \right. . \end{aligned}$$
(58)

The finite time stability of zero for the sliding mode dynamics (58) is proven through the following theorem.

Theorem 4

Zero equilibrium point of the fractional-order system (58) is finite time stable.

Proof

Choose a Lyapunov function candidate as follows.

$$\begin{aligned} V_4 \left( t \right) =\frac{1}{2}\left( {x^{2}+y^{2}+z^{2}} \right) \end{aligned}$$
(59)

Taking fractional derivative of \(V_4 \left( t \right) \) and using Lemma 2, one has

$$\begin{aligned} D^{q}V_4 \left( t \right) \le xD^{q}x+yD^{q}y+zD^{q}z \end{aligned}$$
(60)

Based on the sliding mode dynamics (58), one can obtain

$$\begin{aligned}&{D^q}{V_4}\left( t \right) \le x\left( {y\cdot f\left( {x, y, z} \right) + z\cdot \varphi \left( {x, y, z} \right) - \alpha x}\right. \nonumber \\&\left. +\, {\Delta _x}\left( {x, y, z, t} \right) \right) + y\left( { - \left( {x\cdot f\left( {x, y, z} \right) }\right. }\right. \nonumber \\&\left. {\left. {+\, z\cdot h\left( {x, y, z} \right) + \left( {\beta + {\delta _x}\left| x \right| + {\delta _z}\left| z \right| } \right) \hbox {sgn}\left( y \right) } \right) } \right) \nonumber \\&+\, z\left( {y\cdot h\left( {x, y, z} \right) - x\cdot \varphi \left( {x, y, z} \right) - \gamma z}\right. \nonumber \\&\left. +\, {\Delta _z}\left( {x, y, z, t} \right) \right) \le - \alpha {x^2} + \left| x \right| \left| {{_x}\left( {x, y, z, t} \right) } \right| \nonumber \\&-\, \left( {\beta + {\delta _x}\left| x \right| + {\delta _z}\left| z \right| } \right) \left| y \right| \nonumber \\&-\, \gamma {z^2} + \left| z \right| \left| {{\Delta _z}\left( {x, y, z, t} \right) } \right| \end{aligned}$$
(61)

Using the inequalities (56), one gets

$$\begin{aligned}&D^{q}V_4 \left( t \right) {\le } -\alpha x^{2}{+}\left| x \right| \left| y \right| \delta _x {-}\left( {\beta {+}\delta _x \left| x \right| {+}\delta _z \left| z \right| } \right) \left| y \right| \nonumber \\&\quad -\,\gamma z^{2}+\left| z \right| \left| y \right| \delta _z =-\alpha x^{2}-\beta \left| y\right| -\gamma z^{2}\le 0 \end{aligned}$$
(62)

One can see that (62) gets the same result as obtained in (19). Thus, a similar approach done in Theorem 1 can easily conclude that the origin is the finite time stable equilibrium point of the mismatched system (55) with a settling time \(T_4 \le \root q \of {\frac{2\sqrt{0.5}\varGamma \left( {q+1} \right) \left( {V_4 \left( 0 \right) } \right) ^{0.5}}{\beta \eta }}\). Therefore, the proof is ended. \(\square \)

Now, according to the sliding surface (57), the new robust control law is proposed as follows.

$$\begin{aligned} \vartheta \left( t \right)= & {} -\big (g\left( {x,y,z} \right) -\beta y+x\cdot f\left( {x,y,z} \right) \nonumber \\&+z\cdot h\left( {x,y,z} \right) \nonumber \\&+D^{-q}\left[ {\left( {{\mu }\Vert \left( {x,y,z} \right) \Vert +L} \right) \hbox {sgn}\left( {\upsigma } \right) } \right] \big ) \end{aligned}$$
(63)

where \(L>{\rho }+{\theta }+{\upgamma }\) is a positive constant with \(\left| {D^{q}\left( {\delta _x \left| x \right| +\delta _z \left| z \right| } \right) } \right| \le {\upgamma }\).

Theorem 5

Consider the mismatched uncertain chaotic fractional-order system (55) is controlled by the control signal (63). The states of this system will approach the sliding surface \({\upsigma }\left( t \right) =0\) in finite time.

Proof

Selecting a Lyapunov function candidate in the form of \(V_5 \left( t \right) =\frac{1}{2}{\upsigma }^{2}\) and taking fractional derivative of it, one can obtain

$$\begin{aligned} D^{q}V_5 \left( t \right) \le {\upsigma }D^{q}{\upsigma } \end{aligned}$$
(64)

Based on Lemma 2 and using the system dynamics (45) and the sliding surface (13), one gets

$$\begin{aligned} D^{q}V_5 \left( t \right)\le & {} {\upsigma }D^{q}\left[ {g\left( {x,y,z} \right) -{\beta }y + \Delta \left( {x,y,z} \right) +\hbox {d}\left( t \right) }\right. \nonumber \\&+\vartheta \left( t \right) +\left( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) }\right. \nonumber \\&\left. {\left. {+\left( {\beta +\delta _x \left| x \right| +\delta _z \left| z \right| } \right) \hbox {sgn}\left( y \right) } \right) } \right] \end{aligned}$$
(65)

It is obvious that

$$\begin{aligned}&D^{q}V_5 \left( t \right) {\le } {\upsigma }D^{q}\left[ {g\left( {x,y,z} \right) {-}\beta y{+}\vartheta \left( t \right) }\right. \nonumber \\&\left. +\left( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) } \right) \right] \nonumber \\&+\left| s \right| \left( {\left| {D^{q}\Delta \left( {x,y,z} \right) } \right| }\right. \nonumber \\&\left. +\left| {D^{q}\text {d}\left( t \right) } \right| +\left| {D^{q}\left( {\delta _x \left| x \right| +\delta _z \left| z \right| } \right) } \right| \right) \end{aligned}$$
(66)

Applying Assumption 3 and the condition in (63), one gets

$$\begin{aligned}&D^{q}V_5 \left( t \right) \le {\upsigma }D^{q}\left[ g\left( {x,y,z} \right) -\beta y+\vartheta \left( t \right) \right. \nonumber \\&\left. +\left( x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) \right) \right] \nonumber \\&+\left| s \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert +\rho +\theta +{\upgamma }} \right) \end{aligned}$$
(67)

Inserting \(\vartheta \left( t \right) \) from (63) into the above inequality, we have

$$\begin{aligned}&D^{q}V_5 \left( t \right) \le {\upsigma }D^{q}\left[ {g\left( {x,y,z} \right) -\beta y-\left( {g\left( {x,y,z} \right) }\right. }\right. \nonumber \\&-\beta y+x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) \nonumber \\&\left. {\left. {+D^{-q}\left[ {\left( {{\mu }\Vert \left( {x,y,z} \right) \Vert +L} \right) \hbox {sgn}\left( {\upsigma } \right) } \right] } \right) }\right. \nonumber \\&\left. {+\left( {x\cdot f\left( {x,y,z} \right) +z\cdot h\left( {x,y,z} \right) +\beta \hbox {sgn}\left( y \right) } \right) } \right] \nonumber \\&+\left| s \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert +\rho +\theta +{\upgamma }} \right) \end{aligned}$$
(68)

Simplifying the above inequality, we have

$$\begin{aligned}&D^{q}V_5 \left( t \right) {\le } -{\upsigma }D^{q}\left[ {D^{-q}\left[ {\left( {{\mu }\Vert \left( {x,y,z} \right) \Vert {+}L} \right) \hbox {sgn}\left( {\upsigma } \right) } \right] }\right. \nonumber \\&\left. {-\beta \hbox {sgn}\left( y \right) } \right] +\left| s \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert +\rho +\theta +{\upgamma }} \right) \end{aligned}$$
(69)

\(\square \)

On the basis of Property 1 and \(D^{q}\left[ {\beta \hbox {sgn}\left( y \right) } \right] =0\), one obtains

$$\begin{aligned}&D^{q}V_5 \left( t \right) {\le } \!-\left( {L{+}\mu \Vert \left( {x,y,z} \right) \Vert } \right) \left| {\upsigma } \right| {+}\left| {\upsigma } \right| \left( {\mu \Vert \left( {x,y,z} \right) \Vert }\right. \nonumber \\&\left. {+\rho +\theta +{\upgamma }} \right) \le -\left( {L-{\rho }-{\theta }-{\upgamma }} \right) \left| {\upsigma } \right| \le 0 \end{aligned}$$
(70)

Therefore, on the basis of Lemma 1, one concludes that the states of the uncertain system (55) will attain the sliding surface (57) asymptotically. Besides, a similar strategy utilized in Eqs. (41)–(44) can be applied to indicate that the sliding motion occurs in finite time \(T_5 \le \root q \of {\frac{2\sqrt{0.5}\varGamma \left( {q+1} \right) \left( {V_5 \left( 0 \right) } \right) ^{0.5}}{L-{\rho }-{\theta }-{\upgamma }}}\). This ends the proof.

5 Simulation results

This section provides two numerical simulations for illustrating the effective performance of the proposed non-smooth single-input controller in chaos control of fractional chaotic systems with and without uncertain terms and external disturbances. The predictor-corrector approach described in [40] with a step time of 0.0001 is applied to solve the fractional-order equations in MATLAB software environment.

5.1 Chaos control of fractional Lorenz system

This example employs the introduced non-smooth finite time sliding mode approach for chaos control of fractional-order Lorenz system [27] without system uncertainties and external disturbances. The dynamic equations of the fractional Lorenz system are given as follows.

$$\begin{aligned} \left\{ {{\begin{array}{l} {D^{q}x=a\left( {y-x} \right) } \\ {D^{q}y=x\left( {b-z} \right) -y+u\left( t \right) } \\ {D^{q}z=xy-cz} \\ \end{array} }} \right. \end{aligned}$$
(71)

where \(a=10\), \(b=28\), \(c=8/3\) and \(q=0.94\) are selected to ensure the chaotic behavior for the fractional Lorenz system [27].

According to (13), the following sliding surface is taken into account.

$$\begin{aligned} s\left( t \right) =D^{0.94}y+ax+xz+\hbox {sgn}\left( y \right) \end{aligned}$$
(72)

The sliding control law is also designed based on Eq. (34) as below.

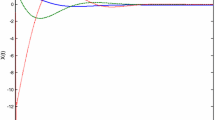
$$\begin{aligned} u\left( t \right)= & {} -(x\left( {28-z} \right) -y+10x\nonumber \\&\quad +\,xz+0.1D^{-0.94}\left( {\hbox {sgn}\left( s \right) } \right) ) \end{aligned}$$
(73)

The initial states of the system are randomly assigned as \(x\left( 0 \right) =3\), \(y\left( 0 \right) =-1\) and \(z\left( 0 \right) =2\). The state trajectories of the controlled fractional-order Lorenz system are depicted in Fig. 1. Obviously, the convergence to zero is obtained rapidly in finite time. The time response of the implemented non-smooth sliding surface (72) is shown in Fig. 2. One can see that the sliding surface dynamics possesses desired features such as rapid transient response and finite time convergence to the origin with no steady state error and free of chattering. Figure 3 illustrates the time history of the control signal (73). It is clear that the amplitude of the control input is satisfactory and there is no harmful oscillation on the control curve. Therefore, it can be concluded that the proposed control method can be implemented in physical systems.

Fig. 1
figure 1

State trajectories of the controlled fractional Lorenz system

Full size image
Fig. 2
figure 2

Time response of the sliding surface applied for fractional Lorenz system

Full size image
Fig. 3
figure 3

Time history of the control signal applied for fractional Lorenz system

Full size image

5.2 Stabilization of fractional financial system

This example examines the robustness and efficacy of the proposed finite time sliding mode controller in stabilization of a fractional-order financial system with system variations and external disturbances. The dynamical equations of the uncertain perturbed system are as follows [28].

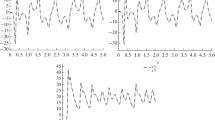
$$\begin{aligned} \left\{ {{\begin{array}{l} {D^{q}x=z+\left( {y-a} \right) x} \\ {D^{q}y=1-by-x^{2}+\Delta \left( {x,y,z} \right) +\text {d}\left( t \right) +u\left( t \right) } \\ {D^{q}z=-x-cz} \\ \end{array} }} \right. \end{aligned}$$
(74)

Time evolution of the state trajectories of the system (74) with the parameters \(a=1\), \(b=0.1\), \(\Delta \left( {x,y,z} \right) =\text {d}\left( t \right) =u\left( t \right) =0\), \(c=1\) and \(q=0.98\) and initial conditions of \(x\left( 0 \right) =0.1\), \(y\left( 0 \right) =0.2\) and \(z\left( 0 \right) =-0.1\) are plotted in Fig. 4. It is seen that the system behavior is oscillatory.

The following uncertain terms and external perturbations are inserted to the dynamics of the system (74).

$$\begin{aligned} \Delta \left( {x,y,z} \right)= & {} 0.1\sin \left( {x+y+z} \right) \nonumber \\ \text {d}\left( t \right)= & {} 0.1\cos \left( t \right) +0.2\hbox {tanh}\left( {20t} \right) \end{aligned}$$
(75)

in which the term \(0.2\hbox {tanh}\left( {20t} \right) \) represents high frequency external noises.

Fig. 4
figure 4

State trajectories of uncontrolled fractional financial system

Full size image
Fig. 5
figure 5

State trajectories of the controlled fractional financial system

Full size image

And, using (13), a sliding surface is designed as follows.

$$\begin{aligned} s\left( t \right) =D^{0.98}y+x^{2}+0.1\hbox {sgn}\left( y \right) \end{aligned}$$
(76)

The sliding control law is realized according to Eq. (47).

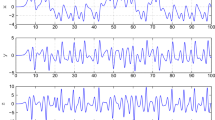
$$\begin{aligned} u\left( t \right)= & {} -\left( \left( {1-x^{2}} \right) -0.1y+x^{2}\right. \nonumber \\&\left. +D^{-0.98}\left( {\left( {\Vert \left( {x,y,z} \right) \Vert +1} \right) \hbox {sgn}\left( s \right) } \right) \right) \end{aligned}$$
(77)

Figure 5 displays the robust state trajectories of the controlled uncertain perturbed fractional-order financial system. One can see that the system states approach to zero with a fast convergence rate, implying that the oscillatory behavior of the original system is suppressed and the effects of system variations and external disturbances are overcame. The time response of the implemented non-smooth sliding surface (76) is illustrated in Fig. 6. It is clear that the sliding surface dynamics exhibits desired transient response and attains to the origin with no steady state error while the chattering is removed. This means that the proposed chattering elimination method does not affect the steady behavior of the system. Figure 7 plots the time history of the control signal (77). Obviously, the control effort is feasible and there is no oscillation on the control curve. Thus, it indicates that the proposed non-smooth finite time control can be realized in practice.

Fig. 6
figure 6

Time response of the sliding surface applied for fractional financial system

Full size image
Fig. 7
figure 7

Time history of the control signal applied for fractional financial system

Full size image

6 Conclusions

The aim of this article is to guarantee the finite time stability of the origin equilibrium point for a class of fractional-order chaotic systems with a single control input. To reach this end, based on the finite time control theory, a non-smooth sliding mode control technology is introduced. Analytical approaches are provided to show that the sliding mode dynamics is finite time stable. To evade the undesirable chattering which inherent in conventional sliding modes, a smooth control law is proposed and validated using the Lyapunov stability criterion. Afterward, the system dynamics is disturbed by unknown variations and fluctuations and the control law is modified to overcome the unwanted terms affecting the system performance. The case of unwanted mismatched uncertainties is also discussed, and appropriate modifications are provided to suit the sliding manifold for such uncertainties. It is shown that the introduced control approach is feasible in practical situations. And numerical simulations reveal that there is no chattering on control input, the control effort is logical, no steady state errors are seen on the output of the system, and fast convergence rate to zero equilibrium is guaranteed. Finally, it is noted that, as a valuable future work, the results of this paper can be extended to the system with time delay with an inspiration of the work [41].