Two-dimensional analytical model of threshold voltage and drain current of a double-halo gate-stacked triple-material double-gate MOSFET

Abstract

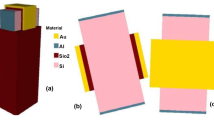
We have developed a two-dimensional analytical model for the channel potential, threshold voltage, and drain-to-source current of a symmetric double-halo gate-stacked triple-material double-gate metal–oxide–semiconductor field-effect transistor (MOSFET). The two-dimensional Poisson’s equation is solved to obtain the channel potential. For accurate modeling of the device, fringing capacitance and effective surface charge are considered. The basic drift–diffusion equation is used to model the drain-to-source current. The midchannel potential of the device is used instead of the surface potential in the current modeling, considering the fact that the punch-through current is not confined only to the surface in a fully depleted MOSFET. An expression for the pinch-off voltage is derived to model the drain current in the saturation region accurately. Various short-channel effects such as drain-induced barrier lowering, gate leakage, threshold voltage, and roll-off have also been investigated. This structure shows excellent ability to suppress various short-channel effects. The results of the proposed model are validated against data obtained from a commercially available numerical device simulator.

Appendices

Appendix 1

The expressions for $G_{j}$ and $H_{j}$ ($j=1,2,3,4,5$) are listed below:

$$\begin{aligned} G_1= & {} \frac{1}{2\sinh \left( {\tau L} \right) }\left[ V_{\mathrm{FD}} +V_{\mathrm{bi}}+V_{\mathrm{DS}} +\frac{\alpha _5}{\tau ^{2}}\right. \nonumber \\&\left. -\left( V_{\mathrm{bi}}+V_{\mathrm{FS}}+\frac{\alpha _1}{\tau ^{2}} \right) \hbox {e}^{-\tau L}\right. \nonumber \\&\left. +\left( {\frac{\alpha _1 -\alpha _2 }{\tau ^{2}}} \right) \cosh \left\{ {\tau \left( L_2+L_3+L_4+L_5\right) } \right\} \right. \nonumber \\&\left. +\left( \frac{\alpha _2-\alpha _3}{\tau ^{2}} \right) \cosh \left\{ \tau \left( L_3+L_4+L_5\right) \right\} \right. \nonumber \\&\left. +\left( \frac{\alpha _3-\alpha _4}{\tau ^{2}}\right) \cosh \left\{ \tau \left( L_4+L_5\right) \right\} \right. \nonumber \\&\left. +\left( \frac{\alpha _4-\alpha _5}{\tau ^{2}}\right) \cosh \left( \tau L_5\right) \right] , \end{aligned}$$

(81)

$$\begin{aligned} G_2= & {} G_1-\left( \frac{\alpha _1 -\alpha _2 }{2\tau ^{2}} \right) \hbox {e}^{-\tau L_1}, \end{aligned}$$

(82)

$$\begin{aligned} G_3= & {} G_1 -\left( \frac{\alpha _1 -\alpha _2 }{2\tau ^{2}} \right) \hbox {e}^{-\tau L_1}\nonumber \\&-\left( \frac{\alpha _2 -\alpha _3 }{2\tau ^{2}}\right) \hbox {e}^{-\tau \left( L_1+L_2\right) }, \end{aligned}$$

(83)

$$\begin{aligned} G_4= & {} G_1 -\left( \frac{\alpha _1 -\alpha _2 }{2\tau ^{2}} \right) \hbox {e}^{-\tau L_1 }-\left( {\frac{\alpha _2 -\alpha _3 }{2\tau ^{2}}} \right) \hbox {e}^{-\tau \left( {{L}_1 +{L}_2 } \right) }\nonumber \\&-\left( {\frac{\alpha _3 -\alpha _4 }{2\tau ^{2}}} \right) \hbox {e}^{-\tau \left( {{L}_1 +{L}_2 +{L}_3 } \right) }, \end{aligned}$$

(84)

$$\begin{aligned} G_5= & {} G_1 -\left( {\frac{\alpha _1 -\alpha _2 }{2\tau ^{2}}} \right) \hbox {e}^{-\tau L_1}-\left( {\frac{\alpha _2 -\alpha _3 }{2\tau ^{2}}} \right) \hbox {e}^{-\tau \left( L_1+L_2\right) }\nonumber \\&-\left( {\frac{\alpha _3 -\alpha _4 }{2\tau ^{2}}} \right) \hbox {e}^{-\tau \left( L_1+L_2+L_3\right) }\nonumber \\&-\left( {\frac{\alpha _4 -\alpha _5 }{2\tau ^{2}}} \right) \hbox {e}^{-\tau \left( {{L}_1 +{L}_2 +{L}_3 +{L}_4 } \right) }, \end{aligned}$$

(85)

$$\begin{aligned} H_1= & {} V_{\mathrm{bi}}-G_1+\frac{\alpha _1}{\tau ^{2}}+V_{\mathrm{FS}}, \end{aligned}$$

(86)

$$\begin{aligned} H_2= & {} H_1-\left( \frac{\alpha _1 -\alpha _2 }{2\tau ^{2}} \right) \hbox {e}^{\tau L_1}, \end{aligned}$$

(87)

$$\begin{aligned} H_3= & {} H_1 -\left( {\frac{\alpha _1 -\alpha _2 }{2\tau ^{2}}} \right) \hbox {e}^{\tau {L}_1 }-\left( {\frac{\alpha _2 -\alpha _3 }{2\tau ^{2}}} \right) \hbox {e}^{\tau \left( {{L}_1 +{L}_2 } \right) },\nonumber \\ \end{aligned}$$

(88)

$$\begin{aligned} H_4= & {} H_1 -\left( {\frac{\alpha _1 -\alpha _2 }{2\tau ^{2}}} \right) \hbox {e}^{\tau L_1}-\left( {\frac{\alpha _2 -\alpha _3 }{2\tau ^{2}}} \right) \hbox {e}^{\tau \left( L_1+L_2\right) }\nonumber \\&-\left( \frac{\alpha _3 -\alpha _4 }{2\tau ^{2}}\right) \hbox {e}^{\tau \left( L_1+L_2+L_3\right) }, \end{aligned}$$

(89)

$$\begin{aligned} H_5= & {} H_1-\left( \frac{\alpha _1-\alpha _2}{2\tau ^{2}} \right) \hbox {e}^{\tau L_1}-\left( \frac{\alpha _2 -\alpha _3 }{2\tau ^{2}}\right) \hbox {e}^{\tau \left( L_1+L_2\right) }\nonumber \\&-\left( \frac{\alpha _3 -\alpha _4 }{2\tau ^{2}} \right) \hbox {e}^{\tau \left( {{L}_1 +{L}_2 +{L}_3 } \right) }\nonumber \\&-\left( {\frac{\alpha _4 -\alpha _5 }{2\tau ^{2}}} \right) \hbox {e}^{\tau \left( {{L}_1 +{L}_2 +{L}_3 +{L}_4 } \right) }. \end{aligned}$$

(90)

Appendix 2

The expressions for ${V}_{\mathrm{thL}}$ and $U_{1}$–$U_{7}$ are given below:

$$\begin{aligned} V_{\mathrm{thL}}= & {} \frac{{qN}_{\mathrm{eff}}}{\epsilon _{\mathrm{Si}} \tau ^{2}}+V_{\mathrm{fb2}} +2\varphi _\mathrm{F}, \end{aligned}$$

(91)

$$\begin{aligned} U_1= & {} \frac{V_1 \left( {\hbox {e}^{-\tau {L}}-1} \right) }{2\sinh \left( {\tau {L}} \right) }-\frac{{V}_6 \left( {\hbox {e}^{-\tau {L}}-1} \right) }{\sinh \left( {\tau {L}} \right) }-V_6\nonumber \\&-\frac{{V}_{\mathrm{FD}} ^{\mathrm{th}}\left( {\hbox {e}^{-\tau {L}}-1} \right) }{2\left\{ {\sinh \left( {\tau {L}} \right) } \right\} ^{2}} -\frac{{V}_{\mathrm{FD}}^{\mathrm{th}}}{2\sinh \left( {\tau {L}} \right) }, \end{aligned}$$

(92)

$$\begin{aligned} U_2= & {} \left\{ {\frac{\left( {\hbox {e}^{-\tau L}-1} \right) }{2\sinh \left( \tau L\right) }}\right\} ^{2}, \end{aligned}$$

(93)

$$\begin{aligned} U_3= & {} V_1V_6-V_6^{2}, \end{aligned}$$

(94)

$$\begin{aligned} U_4= & {} \frac{2V_1V_{\mathrm{FD}}^{\mathrm{th}}}{\sinh \left( {\tau L} \right) }+4\left[ \left\{ \frac{V_{\mathrm{FD}}^{\mathrm{th}}}{2\sinh \left( {\tau L}\right) }\right\} ^{2}+\frac{V_6V_{\mathrm{FD}} ^{\mathrm{th}}}{\sinh \left( \tau L\right) }\right] ,\nonumber \\ \end{aligned}$$

(95)

$$\begin{aligned} U_5= & {} V_{\mathrm{fb1}}+2\varphi _\mathrm{F}+\gamma \sqrt{2\varphi _\mathrm{F}}, \end{aligned}$$

(96)

$$\begin{aligned} U_6= & {} \frac{2{V}_{\mathrm{FD}}^{\mathrm{th}}\hbox {e}^{-\tau L}}{\left\{ \sinh \left( \tau L\right) \right\} ^{2}}-\frac{4V_6 \hbox {e}^{-\tau L}}{\sinh \left( \tau L\right) }-\frac{2V_1\hbox {e}^{-\tau L}}{\sinh \left( \tau L\right) }, \end{aligned}$$

(97)

$$\begin{aligned} U_7= & {} \left\{ \frac{\hbox {e}^{-\tau L}}{\sinh \left( \tau L\right) }\right\} ^{2}, \end{aligned}$$

(98)

$$\begin{aligned} U_8= & {} \frac{2\hbox {e}^{-\tau L}\left( \hbox {e}^{-\tau L}-1 \right) }{\left\{ \sinh \left( {\tau {L}} \right) \right\} ^{2}}+\frac{2\hbox {e}^{-\tau L}}{\sinh \left( \tau {L}\right) }, \end{aligned}$$

(99)

where $V_{\mathrm{FD}}^{\mathrm{th}}=V_{\mathrm{FD}}$ at $V_{\mathrm{GS}}=V_{\mathrm{th}}$ and $V_{\mathrm{thL}}$ is the long-channel threshold voltage, which is independent of channel length.

$$\begin{aligned} V_{j}= & {} V_{\mathrm{bi}}+\frac{{qN}_{\mathrm{eff}}}{\epsilon _{\mathrm{Si}} \tau ^{2}}+V_{\mathrm{fb}j}; \quad j=1,2,3,4,5, \end{aligned}$$

(100)

$$\begin{aligned} V_6= & {} \frac{1}{2\sinh \left( {\tau L}\right) }\left[ V_{\mathrm{DS}}+V_5 -V_1 \hbox {e}^{-\tau L}\right. \nonumber \\&\left. +(V_1-V_2)\cosh \left\{ \tau \left( L_2+L_3+L_4+L_5\right) \right\} \right. \nonumber \\&\left. +(V_2-V_3)\cosh \left\{ \tau \left( L_3+L_4+L_5 \right) \right\} \right. \nonumber \\&\left. +(V_3-V_4)\cosh \left\{ \tau \left( L_4 +L_5\right) \right\} \right. \nonumber \\&\left. +(V_4-V_5)\cosh \left( \tau L_5\right) \right] . \end{aligned}$$

(101)