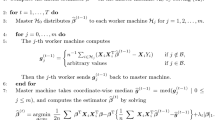Distributed optimization and statistical learning for large-scale penalized expectile regression

Abstract

Large-scale data from various research fields are not only heterogeneous and sparse but also difficult to store on a single machine. Expectile regression is a popular alternative for modeling heterogeneous data. In this paper, we devise a distributed optimization approach to SCAD and adaptive LASSO penalized expectile regression, where the observations are randomly partitioned across multiple machines. We construct a penalized communication-efficient surrogate loss (CSL) function. Computationally, our method based on the CSL function requires only the master machine to solve a regular M-estimation problem, while other worker machines compute the gradient of the loss function on local data. Our method matches the estimation error bound of the centralized method during consecutive rounds of communication. Under some mild assumptions, we establish the oracle properties of the SCAD and adaptive LASSO penalized expectile regression. We then develop a modified alternating direction method of multipliers (ADMM) algorithm for the implementation of the proposed estimator. A series of simulation studies are conducted to assess the finite-sample performance of the proposed estimator. Applications to an HIV study demonstrate the practicability of the proposed method.

Appendix: Proof of Theorem

Proof of Theorem 1

The proposed likelihood function ${\widetilde{L}}_{\text {SCAD}}(\beta )$ is not a convex function. In this case, we should consider the local minimizer instead of the global one ${\widehat{\beta }}^{(\text {SCAD})}$. To avoid confusion, we still denote the local solution by ${\widehat{\beta }}^{(\text {SCAD})}$. Inspired by the idea of Pollard (1991) and Fan and Li (2001), we show that for any given $\delta >0$, there exists a large enough constant c, such that

$$\begin{aligned} \text {P}\left[ \inf _{\left\| u\right\| _{2}=c} {\widetilde{L}}_{\text {SCAD}}\left( \beta _{0}+\frac{u}{\sqrt{n}} \right) >{\widetilde{L}}_{\text {SCAD}}(\beta _{0}) \right] \ge 1-\delta . \end{aligned}$$

(18)

Note that (18) shows that there exists a local minimum in the ball $\left\{ \beta _{0}+\frac{u}{\sqrt{n}}: \left\| u\right\| _{2}\le c\right\}$, which implies that there exists a local minimizer such that $\left\| {\widehat{\beta }}^{(\text {SCAD})}-\beta _{0}\right\| _{2}=O_{p}(n^{-\frac{1}{2}})$. By these facts, the proof of Theorem 1 will be complete if we can show that $n[{\widetilde{L}}_{\text {SCAD}}(\beta _{0}+\frac{u}{\sqrt{n}})$ $-{\widetilde{L}}_{\text {SCAD}}(\beta _{0})]$ is dominated when $\left\| u\right\| _{2}$ equal to sufficiently large c.

For simplicity, the dataset stored on the first machine are denoted by $\{x_{1i}, y_{1i}\}\overset{\wedge }{=}\{x_{i}, y_{i}\}_{i=1}^{n}$. Let ${\overline{\epsilon }}_{i}=y_{i}-x_{i}^{\text {T}}{\overline{\beta }}$, ${\overline{\epsilon }}_{ji}=y_{ji}-x_{ji}^{\text {T}}{\overline{\beta }}$, $\varphi _{\tau }(u)=2\tau uI(u >0)+2(1-\tau )uI(u \le 0)$, $\nabla F({\overline{\beta }})\overset{\wedge }{=}\nabla L_{N}({\overline{\beta }})-\nabla L_{1}({\overline{\beta }})$, $\epsilon _{i}=y_{i}-x_{i}^{\text {T}}\beta _{0}$, by performing a simple calculation, we have $\nabla F({\overline{\beta }})=\frac{1}{n}\mathop {\sum }\nolimits _{i=1}^{n} x_{i}\varphi _{\tau }({\overline{\epsilon }}_{i})-\frac{1}{mn}\mathop {\sum }\nolimits _{j=1}^{m} \mathop {\sum }\nolimits _{i=1}^{n} x_{ji}\varphi _{\tau }({\overline{\epsilon }}_{ji})$. Thus

$$\begin{aligned}&n\left[ {\widetilde{L}}_{\text {SCAD}}\left( \beta _{0}+\frac{u}{\sqrt{n}} \right) -{\widetilde{L}}_{\text {SCAD}}(\beta _{0}) \right] \nonumber \\&\quad =n\left[ L_{1}\left( \beta _{0}+\frac{u}{\sqrt{n}} \right) -L_{1}(\beta _{0})+\left\langle \nabla F({\overline{\beta }}),\frac{u}{\sqrt{n}}\right\rangle \right. \nonumber \\&\qquad \left. +\sum _{k=1}^{p}p_{\lambda } \left( \left| \beta _{0k}+\frac{u_{k}}{\sqrt{n}}\right| \right) -\sum _{k=1}^{p}p_{\lambda }(\left| \beta _{0k}\right| )\right] \nonumber \\&\quad =\text {I}+\text {II}+\text {III}. \end{aligned}$$

(19)

where $\text {I}=\mathop {\sum }\limits _{i=1}^{n} \left[ \rho _{\tau }\left( \epsilon _{i}-\frac{x_{i}^{\text {T}}u}{\sqrt{n}} \right) - \rho _{\tau }(\epsilon _{i}) \right]$, $\text {II}=u^{\text {T}}\left[ \frac{1}{\sqrt{n}}\mathop {\sum }\limits _{i=1}^{n} \left( x_{i}\varphi _{\tau }({\overline{\epsilon }}_{i})-\frac{1}{m} \sum _{j=1}^{m}x_{ji}\varphi _{\tau }({\overline{\epsilon }}_{ji}) \right) \right]$, $\text {III}=n\mathop {\sum }\limits _{k=1}^{p} \left[ p_{\lambda }\left( \left| \beta _{0k}+\frac{u_{k}}{\sqrt{n}}\right| \right) -p_{\lambda } (\left| \beta _{0k}\right| ) \right]$.

Under Assumptions (A1) and (A2), similarly to the arguments of Zhao and Zhang (2018), we obtain

$$\begin{aligned} \text {I}=g(\tau )u^{\text {T}}\left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] u-u^{\text {T}}\left[ \frac{1}{\sqrt{n}}\mathop {\sum }\limits _{i=1}^{n} x_{i}\varphi _{\tau }(\epsilon _{i}) \right] +o_{p}(1), \end{aligned}$$

(20)

where $g(\tau )=\tau (1-F_{\epsilon }(0))+(1-\tau )F_{\epsilon }(0)$. Therefore, we obtain

$$\begin{aligned} \text {I}+\text {II}=&g(\tau )u^{\text {T}}\left[ \frac{\sum _{i=1}^{n} x_{i}x_{i}^{\text {T}}}{n} \right] u\nonumber \\&+u^{\text {T}}\left[ \frac{1}{\sqrt{n}}\mathop {\sum }\limits _{i=1}^{n} \left( x_{i}\varphi _{\tau }({\overline{\epsilon }}_{i})-\frac{1}{m} \sum _{j=1}^{m}x_{ji}\varphi _{\tau }({\overline{\epsilon }}_{ji})-x_{i} \varphi _{\tau }(\epsilon _{i}) \right) \right] +o_{p}(1)\nonumber \\ =&g(\tau )u^{\text {T}}\left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] u +W_{n}^{\text {T}}u+o_{p}(1) \overset{\wedge }{=}G_{n}(u), \end{aligned}$$

(21)

where $W_{n}=\frac{1}{\sqrt{n}}\mathop {\sum }\limits _{i=1}^{n} D_{i}$, and

$$\begin{aligned} D_{i}=\xi _{i}-\frac{\eta _{i}}{m}-\zeta _{i}=\left( I_{p\times p},-\frac{I_{p\times p}}{m},-I_{p\times p} \right) _{p\times 3p}\left( \begin{array}{c} \xi _i \\ \eta _i \\ \zeta _i\\ \end{array} \right) _{3p\times 1},\qquad i=1,\ldots ,n \end{aligned}$$

with $\xi _{i}=x_{i}\varphi _{\tau }({\overline{\epsilon }}_{i})$, $\eta _{i}=\mathop {\sum }\limits _{j=1}^{m} x_{ji}\varphi _{\tau }({\overline{\epsilon }}_{ji})$, $\zeta _i=x_i\varphi _{\tau }(\epsilon _i)$ and $I_{p\times p}$ is the p-order identity matrix.

Under the Assumption (A2) that $\tau$-expectile of the error term is zero, we derive $\text {E}\left[ \varphi _{\tau }({\overline{\epsilon }}_{i}) \right] =\text {E}\left[ \varphi _{\tau } ({\overline{\epsilon }}_{ji}) \right] =\text {E}\left[ \varphi _{\tau }(\epsilon _{i}) \right] =0$, and

$$\begin{aligned} \text {Cov}(\xi _{i},\xi _{i})&=Ax_{i}x_{i}^{\text {T}},\qquad \text {Cov}(\eta _{i},\eta _{i})=A\mathop {\sum }\limits _{j=1}^{m} x_{ji}x_{ji}^{\text {T}},\qquad \text {Cov}(\zeta _i,\zeta _i)=4c(\tau )x_{i}x_{i}^{\text {T}},\\ \text {Cov}(\xi _{i},\eta _{i})&=Ax_{i}x_{i}^{\text {T}},\qquad \text {Cov}(\xi _{i},\zeta _i)=Bx_{i}x_{i}^{\text {T}},\qquad \text {Cov}(\eta _{i},\zeta _i)=Bx_{i}x_{i}^{\text {T}}, \end{aligned}$$

where $c(\tau )=\tau ^{2}\text {E}\left[ \epsilon _{i}^{2}I(\epsilon _{i}>0) \right] +(1-\tau )^{2}\text {E}\left[ \epsilon _{i}^{2}I(\epsilon _{i}\le 0) \right]$, $A=\text {Var}\left[ \varphi _{\tau }({\overline{\epsilon }}_{i}) \right]$, $B=\text {Cov}(\varphi _{\tau }({\overline{\epsilon }}_{i}),\varphi _{\tau }(\epsilon _{i}))$. Therefore,

$$\begin{aligned} W\overset{\wedge }{=}\text {Var}\left( \begin{array}{c} \xi _{i} \\ \eta _{i} \\ \zeta _{i} \end{array} \right) =\left( \begin{array}{ccc} Ax_{i}x_{i}^{\text {T}} &{} Ax_{i}x_{i}^{\text {T}} &{} Bx_{i}x_{i}^{\text {T}} \\ Ax_{i}x_{i}^{\text {T}} &{} A\mathop {\sum }\limits _{j=1}^{m} x_{ji}x_{ji}^{\text {T}} &{} Bx_{i}x_{i}^{\text {T}} \\ Bx_{i}x_{i}^{\text {T}} &{} Bx_{i}x_{i}^{\text {T}} &{} 4c(\tau )x_{i}x_{i}^{\text {T}} \end{array} \right) . \end{aligned}$$

(22)

By the fact that $D_{i}$ is independent and identically distributed zero-mean random vectors and Assumption (A2), we have

$$\begin{aligned} \text {Var}\left[ W_{n} \right] =&\frac{1}{n}\mathop {\sum }\limits _{i=1}^{n} (I_{p\times p},-\frac{I_{p\times p}}{m},-I_{p\times p})W\left( \begin{array}{c} I_{p\times p} \\ -\frac{I_{p\times p}}{m}\\ -I_{p\times p} \end{array} \right) \nonumber \\ =&\frac{1}{n}\mathop {\sum }\limits _{i=1}^{n}\left[ \left( \frac{m-2}{m}A +\frac{2-2m}{m}B+4c(\tau ) \right) x_{i}x_{i}^{\text {T}}+\frac{A}{m^{2}} \sum _{j=1}^{m}x_{ji}x_{ji}^{\text {T}} \right] \nonumber \\&\xrightarrow {\ \text {P}\ }m^{-1}h(m,\tau )\varSigma , \qquad \text {as}\quad n \longrightarrow \infty , \end{aligned}$$

(23)

where $h(m,\tau )=\left[ (m-1)A+(2-2m)B+4mc(\tau ) \right]$ . By central limit theorem, we have

$$\begin{aligned} W_{n}=\frac{1}{\sqrt{n}}\sum _{i=1}^{n}D_{i}\xrightarrow {\ d\ }N(0, m^{-1}h(m,\tau )\varSigma ). \end{aligned}$$

(24)

Therefore, $W_{n}^{\text {T}}u$ is bounded in probability, i.e.

$$\begin{aligned} W_{n}^{\text {T}}u=O_{p}\left(\sqrt{m^{-1}h(m,\tau )u^{\text {T}}\varSigma u}\right). \end{aligned}$$

(25)

Owing to the fact that

$$\begin{aligned} \text {III}=\,&n\sum _{k=1}^{p}\left[ p_{\lambda }\left( \left| \beta _{0k} +\frac{u_{k}}{\sqrt{n}}\right| \right) -p_{\lambda }(\left| \beta _{0k}\right| ) \right] \\ \ge\,&n\sum _{k=1}^{s}\left[ p_{\lambda }\left( \left| \beta _{0k} +\frac{u_{k}}{\sqrt{n}}\right| \right) -p_{\lambda }(\left| \beta _{0k}\right| ) \right] . \end{aligned}$$

For the SCAD penalty $p_{\lambda }(\theta )$, we have $p_{\lambda }^{'}(\theta )\equiv 0$ for $\theta \in [a\lambda ,+\infty )$, that is, $p_{\lambda }(\theta )$ is constant if $\theta \ge a\lambda$. Thus, if $\lambda =\lambda (n)\longrightarrow 0$, we obtain

$$\begin{aligned} n\sum _{k=1}^{s}\left[ p_{\lambda }\left( \left| \beta _{0k}+\frac{u_{k}}{\sqrt{n}}\right| \right) -p_{\lambda }(\left| \beta _{0k}\right| ) \right] =0 \end{aligned}$$

(26)

uniformly in any compact subset of $R^{p}$.

By assumption (A2) and (21), (25) and (26), $n\left[ {\widetilde{L}}_{\text {SCAD}}(\beta _{0}+\frac{u}{\sqrt{n}})- {\widetilde{L}}_{\text {SCAD}}(\beta _{0}) \right]$ is dominated by the term $g(\alpha )u^{\text {T}}\varSigma u$, when $\left\| u\right\| _{2}=c$ large enough. Thus, we have ${\widehat{\beta }}^{(\text {SCAD})}\xrightarrow {\ \text {P}\ }\beta _{0}$, as $n\longrightarrow \infty$. Owing to $N=nm$, if $\lambda =\lambda (N)\longrightarrow 0$, we have ${\widehat{\beta }}^{(\text {SCAD})}\xrightarrow {\ \text {P}\ }\beta _{0}$, as $N\longrightarrow \infty$. $\square$

Proof of Theorem 2

In order to prove the sparsity result, we should show that: if $\lambda =\lambda \left( n \right) \rightarrow 0$, and $\sqrt{n}\lambda \rightarrow \infty$ as $n\rightarrow \infty$, then with probability tending to one, any given $\beta _{1}$ satisfying $\parallel \beta _{1}-\beta _{10}\parallel _{2}=O_{p}\left( n^{-\frac{1}{2}} \right)$ and any constant c,

$$\begin{aligned} \left( \beta _{1}^{\text {T}},0^{\text {T}} \right) ^{\text {T}}=\arg \mathop {\min }\limits _{\parallel \beta _{2} \parallel \le {cn^{-\frac{1}{2}}}}{\widetilde{L}}_{\text {SCAD}} \left( \left( \beta _{1}^{\text {T}},\beta _{2}^{\text {T}} \right) ^{\text {T}} \right) , \end{aligned}$$

i.e., for any $\delta >0$

$$\begin{aligned} \text {P}\left[ \mathop {\inf }\limits _{\left\| \beta _{2}\right\| \le {cn^{-\frac{1}{2}}}} {\widetilde{L}}_{\text {SCAD}}\left( \left( \beta _{1}^{\text {T}}, \beta _{2}^{\text {T}} \right) ^{\text {T}} \right) >{\widetilde{L}}_{\text {SCAD}} \left( \left( \beta _{1}^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) \right] \ge 1-\delta . \end{aligned}$$

(27)

By performing a simple calculation, we obtain

$$\begin{aligned}&n\left[ {\widetilde{L}}_{\text {SCAD}}\left( \left( \beta _{1}^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) -{\widetilde{L}}_{\text {SCAD}}\left( \left( \beta _{1}^{\text {T}}, \beta _{2}^{\text {T}} \right) ^{\text {T}} \right) \right] \nonumber \\&\quad =n\left[ {\widetilde{L}}_{\text {SCAD}} \left( \left( \beta _{1}^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) -{\widetilde{L}}_{\text {SCAD}} \left( \left( \beta _{10}^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) \right] \nonumber \\&\qquad -n\left[ {\widetilde{L}}_{\text {SCAD}}\left( \left( \beta _{1}^{\text {T}}, \beta _{2}^{\text {T}} \right) ^{\text {T}} \right) -{\widetilde{L}}_{\text {SCAD}} \left( \left( \beta _{10}^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) \right] \nonumber \\&\quad =g\left( \tau \right) \sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},0^{\text {T}} \right) \left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] \sqrt{n} \left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},0^{\text {T}} \right) ^{\text {T}}\nonumber \\&\qquad +\sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},0^{\text {T}} \right) W_{n}\nonumber \\&\qquad -g\left( \tau \right) \sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}}, \beta _{2}^{\text {T}} \right) \left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] \sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},\beta _{2}^{\text {T}} \right) ^{\text {T}}\nonumber \\&\qquad -\sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},\beta _{2}^{\text {T}} \right) W_{n}\nonumber \\&\qquad -n\sum _{k=s+1}^{p}p_{\lambda }\left( \left| \beta _{k}\right| \right) +o_{p}\left( 1 \right) . \end{aligned}$$

(28)

Based on the given conditions $\left\| \beta _{1}-\beta _{10}\right\| _{2}=O_{p}\left( n^{-\frac{1}{2}} \right)$ and $\left\| \beta _{2}\right\| \le {cn^{-\frac{1}{2}}}$, and Assumption (A2), we summarize the results as

$$\begin{aligned}&g\left( \tau \right) \left( \sqrt{n}\left( \beta _{1}-\beta _{10} \right) ^{\text {T}},0^{\text {T}} \right) \left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] \left( \sqrt{n} \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},0^{\text {T}} \right) ^{\text {T}}=O_{p}\left( 1 \right) ,\nonumber \\&g\left( \tau \right) \sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}}, \beta _{2}^{\text {T}} \right) \left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] \sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}}, \beta _{2}^{\text {T}} \right) ^{\text {T}}=O_{p}\left( 1 \right) . \end{aligned}$$

(29)

Under the fact (25) in the proof of Theorem 1, we have

$$\begin{aligned}&\sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},0^{\text {T}} \right) W_{n} -\sqrt{n}\left( \left( \beta _{1}-\beta _{10} \right) ^{\text {T}},\beta _{2}^{\text {T}} \right) W_{n}\nonumber \\&\quad =-\sqrt{n}\left( 0^{\text {T}},\beta _{2}^{\text {T}} \right) W_{n} =O_{p}\left( \sqrt{nm^{-1}h\left( m,\tau \right) \beta _{2}^{\text {T}}\varSigma _{22}\beta _{2}} \right) =O_{p}\left( 1 \right) , \end{aligned}$$

(30)

the last equal in (30) relies on the fact that

$$\begin{aligned} n\beta _{2}^{\text {T}}\varSigma _{22}\beta _{2}&=n\sum _{i,j=1}^{p-s}a_{ij} \beta _{2i}\beta _{2j}\le {n}\max \left| a_{ij}\right| \sum _{i,j=1}^{p-s} \beta _{2i}\beta _{2j}\nonumber \\&=n\parallel \varSigma _{22}\parallel _{\infty }\sum _{i,j=1}^{p-s}\beta _{2i} \beta _{2j}=n\parallel \varSigma _{22}\parallel _{\infty }\left( \sum _{i=1}^{p-s} \left| \beta _{2i}\right| \right) \left( \sum _{j=1}^{p-s}\left| \beta _{2j}\right| \right) \nonumber \\&\le {n}\parallel \varSigma _{22}\parallel _{\infty }\parallel \beta _{2} \parallel _{1}^{2}\le \left( p-s \right) \parallel \varSigma _{22}\parallel _{\infty } \times {n}\parallel \beta _{2}\parallel _{2}^{2}=O_{p}\left( 1 \right) \end{aligned}$$

with $\varSigma _{22}=\left( a_{ij} \right) _{i,j=1}^{p-s}$, $\beta _{2}=\left( \beta _{2i} \right) _{i=1}^{p-s}$.

For the SCAD penalty, under the conditions $\lambda =\lambda \left( n \right) \rightarrow 0$ and $\sqrt{n}\lambda \rightarrow \infty$ as $n\rightarrow \infty$, we have

$$\begin{aligned} n\sum _{k=s+1}^{p}p_{\lambda }\left( \left| \beta _{k}\right| \right)&\ge {n}\sum _{k=s+1}^{p} \left( \lambda \varliminf _{\lambda \rightarrow 0}\varliminf _{\theta \rightarrow 0^{+}} \frac{p_{\lambda }^{'}\left( \theta \right) }{\lambda } \beta _{k}\text {sgn}\left( \beta _{k} \right) +o\left( \left| \beta _{k}\right| \right) \right) \nonumber \\&=n\lambda \left( \varliminf _{\lambda \rightarrow 0}\varliminf _{\theta \rightarrow 0^{+}} \frac{p_{\lambda }^{'}\left( \theta \right) }{\lambda } \right) \left( \sum _{k=s+1}^{p}\left( \left| \beta _{k}\right| \right) \right) \left( 1+o\left( 1 \right) \right) \nonumber \\&=n\lambda \left( \sum _{k=s+1}^{p}\left( \left| \beta _{k}\right| \right) \right) \left( 1+o\left( 1 \right) \right) . \end{aligned}$$

(31)

Based on the fact that $\mathop {\lim }\limits _{\lambda \rightarrow 0}\mathop {\lim }\limits _{\theta \rightarrow 0^{+}}\frac{p_{\lambda }^{'}\left( \theta \right) }{\lambda }=1$. Since $\sqrt{n}\lambda \rightarrow \infty$ and $\parallel \beta _{2}\parallel _{2}\le {cn^{-\frac{1}{2}}}$, $n\sum _{k=s+1}^{p}p_{\lambda }\left( \left| \beta _{k}\right| \right)$ is of higher order than $\sqrt{n}$. Then $\mathop {\inf }\limits _{\left\| \beta _{2}\right\| \le {cn^{-\frac{1}{2}}}}{\widetilde{L}}_{\text {SCAD}}\left( \beta _{1},\beta _{2} \right) >{\widetilde{L}}_{\text {SCAD}}\left( \beta _{1},0 \right)$ with probability tending to one. Therefore, we derive result (27) on any compact subset of $\left\{ \beta :\left\| \beta _{1}-\beta _{10}\right\| _{2}=O_{p}\left( n^{-\frac{1}{2}} \right) , \left\| \beta _{2}\right\| _{2}\le {cn^{-\frac{1}{2}}}\right\}$. As $N=nm$, it is easy to show that, $\lambda =\lambda \left( N \right) \rightarrow 0$ and $\sqrt{N}\lambda \rightarrow \infty$ as $N\rightarrow \infty$, we have $\widehat{\beta _{2}}^{(S)}=0$.

In the following, we prove the asymptotic normality of ${\widehat{\beta }}_{1}^{(\text {SCAD})}$. From the definition of ${\widehat{\beta }}^{(\text {SCAD})}$ and the notation (21), we can see that $\sqrt{n}\left( {\widehat{\beta }}_{1}^{(\text {SCAD})}-{\widehat{\beta }}_{10}^{(\text {SCAD})} \right)$ minimizes $G_{n}\left( \left( \theta ^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) +n\sum _{k=1}^{s}p_{\lambda }\left( \left| \beta _{0k}+\frac{\theta _{k}}{\sqrt{n}}\right| \right)$ with respect to $\theta$. The proof of Theorem 1 implies that

$$\begin{aligned} G_{n}\left( \left( \theta ^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right)&=g\left( \tau \right) \left( \theta ^{\text {T}},0^{\text {T}} \right) \left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] \left( \theta ^{\text {T}},0^{\text {T}} \right) ^{\text {T}}\nonumber \\&\quad +W_{n}^{\text {T}}\left( \theta ^{\text {T}},0 \right) ^{\text {T}}+o_{p}\left( 1 \right) +o\left( 1 \right) \nonumber \\&=g\left( \tau \right) \theta ^{\text {T}}\left[ \frac{\sum _{i=1}^{n}x_{i}^{1} (x_{i}^{1})^{\text {T}}}{n} \right] \theta +W_{n,11}^{\text {T}}\theta +o_{p}\left( 1 \right) +o\left( 1 \right) , \end{aligned}$$

(32)

where $W_{n,11}\xrightarrow {d}N\left( 0,m^{-1}h\left( m,\tau \right) \varSigma _{11} \right)$. For large n, under condition $\lambda =\lambda \left( n \right) \rightarrow 0$, we get

$$\begin{aligned} n\sum _{k=1}^{s}p_{\lambda }\left( \left| \beta _{0k}+\frac{\theta _{k}}{\sqrt{n}}\right| \right) =n\sum _{k=1}^{s}p_{\lambda }\left( \left| \beta _{0k}\right| \right) \end{aligned}$$

(33)

uniformly in any compact subset of $R^{s}$, and this term does not depend on the parameter $\theta$. Denote

$$\begin{aligned} \theta _{n}&=\arg \mathop {\min }\limits _{\theta }\left[ G_{n}\left( \left( \theta ^{\text {T}}, 0^{\text {T}} \right) ^{\text {T}} \right) +n\sum _{k=1}^{s}p_{\lambda }\left( \left| \beta _{0k}\right| \right) \right] \nonumber \\&=\left( -2g\left( \tau \right) \frac{\sum _{i=1}^{n}x_{i}^{1}(x_{i}^{1})^{\text {T}}}{n} \right) ^{-1}W_{n,11}. \end{aligned}$$

(34)

From the above results, we have

$$\begin{aligned} \sqrt{n}\left( {\widehat{\beta }}_{1}^{(\text {SCAD})}-\beta _{10} \right)&=\left( -2g\left( \tau \right) \frac{\sum _{i=1}^{n}x_{i}^{1}(x_{i}^{1})^{\text {T}}}{n} \right) ^{-1} W_{n,11}+o_{p}\left( 1 \right) \nonumber \\&\xrightarrow {\ d\ }N\left( 0,\frac{h\left( m,\tau \right) }{4mg^{2}\left( \tau \right) }\varSigma _{11}^{-1} \right) . \end{aligned}$$

(35)

Due to $N=nm$ and the result (35), ${\widehat{\beta }}_{1}^{(\text {SCAD})}$ has the following asymptotic property:

$$\begin{aligned} \sqrt{N}\left( {\widehat{\beta }}_{1}^{(\text {SCAD})}-\beta _{10} \right) \xrightarrow {\ d\ }N\left( 0,\frac{h\left( m,\tau \right) }{4g^{2}\left( \tau \right) }\varSigma _{11}^{-1} \right) , \quad \text {as}\quad N\rightarrow \infty . \end{aligned}$$

Proof of Theorem 3

Similar to (19) in the proof of Theorem 1, we obtain

$$\begin{aligned}&n\left[ {\widetilde{L}}_{\text {AL}}\left( \beta _{0}+\frac{u}{\sqrt{n}} \right) -{\widetilde{L}}_{\text {AL}}\left( \beta _{0} \right) \right] \nonumber \\&\quad =g\left( \tau \right) u^{\text {T}}\left[ \frac{\sum _{i=1}^{n}x_{i}x_{i}^{\text {T}}}{n} \right] u +W_{n}^{\text {T}}u+n\lambda \sum _{k=1}^{p}\left[ {\widetilde{\omega }}_{k} \left| \beta _{0k}+\frac{u_{k}}{\sqrt{n}}\right| -{\widetilde{\omega }}_{k} \left| \beta _{0k}\right| \right] +o_{p}\left( 1 \right) . \end{aligned}$$

(36)

Now consider the third term in (36), for $k=1,\ldots ,s$, the true coefficient $\beta _{0k}\ne 0$, then ${\widetilde{\omega }}_{k}\xrightarrow {\ \text {P}\ }\left| \beta _{0k}\right| ^{-r}$ and $\sqrt{n}\left( \left| \beta _{0k}+\frac{u_{k}}{\sqrt{n}}\right| -\left| \beta _{0k}\right| \right) \rightarrow {u_{k}}\text {sgn}\left( \beta _{0k} \right)$. Thus, by Slutsky’s theorem and $\sqrt{n}\lambda \rightarrow 0$, we have

$$\begin{aligned} \sqrt{n}\lambda \times \sqrt{n}\left[ {\widetilde{\omega }}_{k}\left| \beta _{0k} +\frac{u_{k}}{\sqrt{n}}\right| -{\widetilde{\omega }}_{k}\left| \beta _{0k}\right| \right] \xrightarrow {\ \text {P}\ }0, \qquad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

(37)

On the other hand, for $k=s+1,s+2,\ldots ,p$, we have $\beta _{0k}=0$, so $\sqrt{n}\left( \left| \beta _{0k}+\frac{u_{k}}{\sqrt{n}}\right| -\left| \beta _{0k}\right| \right) =\left| u_{k}\right|$ and $\sqrt{n}\lambda {\widetilde{\omega }}_{k}=n^{\frac{1+r}{2}}\lambda \left( \left| \sqrt{n}{\widehat{\beta }}_{k}\right| \right) ^{-r}$, where $\sqrt{n}{\widehat{\beta }}_{k}=O_{p}\left( 1 \right)$, so it follows that

$$\begin{aligned} n\lambda \left[ {\widetilde{\omega }}_{k}\left| \beta _{0k} +\frac{u_{k}}{\sqrt{n}}\right| -{\widetilde{\omega }}_{k}\left| \beta _{0k}\right| \right] \xrightarrow {\ \text {P}\ }&\left\{ \begin{array}{ll} \infty , &{}\text {when}\quad u_{k}\ne 0, \\ 0, &{}\text {otherwise}. \end{array} \right. \end{aligned}$$

(38)

Thus, from (36), (37), (38) and Slutsky’s theorem and Assumption (A2), we obtain

$$\begin{aligned}&n\left[ {\widetilde{L}}_{\text {AL}}\left( \beta _{0}+\frac{u}{\sqrt{n}} \right) -{\widetilde{L}}_{\text {AL}}\left( \beta _{0} \right) \right] \nonumber \\&\quad \xrightarrow {\ d\ }\text {E}\left( u \right) =\left\{ \begin{array}{ll} g\left( \tau \right) u^{1}\varSigma _{11}u^{1}+W_{n,11}^{\text {T}}u^{1}, &{}\text {when}\quad u_{k}=0, k\ge s+1, \\ \infty , &{}\text {otherwise}. \end{array} \right. \end{aligned}$$

(39)

where $u^{1}=(u_{1},u_{2},\ldots ,u_{s})^{\text {T}}$. Noticing that $n\left[ {\widetilde{L}}_{\text {AL}}\left( \beta _{0}+\frac{u}{\sqrt{n}} \right) -{\widetilde{L}}_{\text {AL}}\left( \beta _{0} \right) \right]$ is convex in u, and $\text {E}\left( u \right)$ has a unique minimier, and we have

$$\begin{aligned} \arg \mathop {\min }\limits _{u}{n}\left[ {\widetilde{L}}_{\text {AL}}\left( \beta _{0} +\frac{u}{\sqrt{n}} \right) \right] =\sqrt{n}\left( {\widehat{\beta }}^{(\text {AL})}- \beta _{0} \right) \xrightarrow {\ d\ }\arg \mathop {\min }\limits _{u}\text {E}\left( u \right) . \end{aligned}$$

(40)

Using (40) and as in the derivation of (35), we obtain

$$\begin{aligned} \sqrt{n}\left( {\widehat{\beta }}_{1}^{(\text {AL})}-\beta _{10} \right) \xrightarrow {\ d\ }N\left( 0,\frac{h\left( m,\tau \right) }{4mg^{2}\left( \tau \right) }\varSigma _{11}^{-1} \right) ,\quad \text {as}\quad n\rightarrow \infty \end{aligned}$$

i.e. when $\sqrt{N}\lambda \rightarrow 0$ and $N^{\frac{r+1}{2}}\lambda \rightarrow \infty$, we have

$$\begin{aligned} \sqrt{N}\left( {\widehat{\beta }}_{1}^{(\text {AL})}-\beta _{10} \right) \xrightarrow {\ d\ }N\left( 0,\frac{h\left( m,\tau \right) }{4g^{2}\left( \tau \right) }\varSigma _{11}^{-1} \right) , \quad \text {as}\quad N\rightarrow \infty . \end{aligned}$$

Next we show the consistency property of the model selection. For any $\beta _{1}-\beta _{10}=O_{p}\left( n^{-\frac{1}{2}} \right)$, $0<\parallel \beta _{2}\parallel <cn^{-\frac{1}{2}}$, similar to (28), we have

$$\begin{aligned} n\left[ {\widetilde{L}}_{\text {AL}}\left( \left( \beta _{1}^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) -{\widetilde{L}}_{\text {AL}}\left( \left( \beta _{1}^{\text {T}},\beta _{2}^{\text {T}} \right) ^{\text {T}} \right) \right] =O_{p}\left( 1 \right) -n\lambda \sum _{k=s+1}^{p}{\widetilde{\omega }}_{k}\left| \beta _{k}\right| . \end{aligned}$$

(41)

By applying the condition $n^{\frac{1+r}{2}}\lambda \rightarrow \infty$ as $n\rightarrow \infty$, we obtain

$$\begin{aligned} n\lambda \sum _{k=s+1}^{p}{\widetilde{\omega }}_{k}\left| \beta _{k}\right| =n^{\frac{1+r}{2}}\lambda \times \sqrt{n}\sum _{j=s+1}^{d}\left( \sqrt{n} \left| {\widehat{\beta }}_{k}\right| \right) ^{-r}\left| \beta _{k}\right| \rightarrow \infty . \end{aligned}$$

Therefore, the second term of (41) goes to $-\infty$ as $n\rightarrow \infty$, which in turn implies that $n\left[ {\widetilde{L}}_{\text {AL}}\left( \left( \beta _{1}^{\text {T}},0^{\text {T}} \right) ^{\text {T}} \right) -{\widetilde{L}}_{\text {AL}}\left( \left( \beta _{1}^{\text {T}},\beta _{2}^{\text {T}} \right) ^{\text {T}} \right) \right] <0$ for large n. Similarly to the explanation of the proof process of Theorem 2 in the corresponding part, we have ${\widehat{\beta }}_{2}^{(\text {AL})}=0$. That is, based on the assumption $\sqrt{N}\lambda \rightarrow \infty$ and $N^{\frac{1+r}{2}}\lambda \rightarrow \infty$, as $N\rightarrow \infty$, we have ${\widehat{\beta }}_{2}^{(\text {AL})}=0$ $\square$