Analytical study of nonlinear oscillatory systems using the Hamiltonian approach technique

Abstract

In this article, we investigate and apply Hamiltonian approach method as one of the analytical approximate techniques, for studying the strongly nonlinear dynamical systems such as the motion of a rigid rod rocking back on the circular surface without slipping and the free vibrations of an autonomous conservative oscillator with inertia and static-type fifth-order nonlinearities. To illustrate the applicability and accuracy of the method, the approximate solution results are compared with exact and numerical solutions.

Introduction

Most of the dynamical systems facing engineers, physicists and applied mathematicians today exhibit certain essential features which preclude exact analytical solutions. Some of these features are nonlinearities, variable coefficients, complex boundary shapes, and nonlinear boundary conditions at known or, in some cases, unknown boundaries. Even if the exact solution of a problem can be found explicitly, it may be useless for mathematical and physical interpretation or numerical evaluation. Examples of such problems are Bessel functions of large argument and large-order and doubly periodic functions. Therefore, to obtain information about solutions of equations, we are forced to resort to approximate and numerical solutions, or combinations of both.

Recently, considerable attention has been directed toward the analytical approximate solutions for the strongly nonlinear differential equations of dynamical systems. The traditional perturbation methods have many shortcomings, and they are not valid for strongly nonlinear dynamical systems.

To overcome the shortcomings, many techniques have appeared in open literature, for example, parameter-expanding method [1–3], variational iteration method [4–7], energy balance method [8–14], variational approach method [15–19], amplitude–frequency formulation [20–22], homotopy perturbation method [23–29], and the other analytical approximate solutions [30].

The solution of differential equations in physics and engineering, especially some oscillation equations are nonlinear, and in most cases it is difficult to solve such equations, especially analytically. Previously, He had introduced the energy balance method based on collocation and the Hamiltonian. This method can be seen as a Ritz method and leads to a very rapid convergence of the solution, and can be easily extended to other nonlinear oscillations.

This approach is very simple but strongly depends upon the chosen location point. Recently, He [31] has proposed the Hamiltonian approach to overcome the shortcomings of the energy balance method. This approach is a kind of energy method with a vast application in conservative oscillatory systems. Application of this method can be found in many literatures [31–35].

The Hamiltonian approach method is the subject of this article, as one of the analytical approximate techniques. In this article, we present two examples to illustrate the applicability, accuracy and effectiveness of the Hamiltonian approach method as one of the analytical approximate techniques.

As the first example in this paper, we investigate the nonlinear differential equation of the motion of a rigid rod rocking back on the circular surface without slipping [36]. In the second example, we investigate the nonlinear differential equation of the free vibrations of an autonomous conservative oscillator with inertia and static-type fifth-order nonlinearities [37].

To illustrate the accuracy of the Hamiltonian approach method, in first example, we compare the approximate solution result with exact solution. In second example, because there is no exact solution, we compare the approximate solution result with Runge–Kutta method as one of the known numerical methods.

The description of Hamiltonian approach method

To descript the He’s Hamiltonian approach method, we consider the following general oscillator [31]:

$$\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)+f(u(t))=0$$

(1)

with initial conditions:

$$u(0)=A,\frac{\text{d}}{\text{d}t}u(0)=0.$$

(2)

It is easy to establish a variational principle for Eq. (1), which reads [31]:

$$J\left(u(t)\right)=\underset{0}{\overset{T/4}{\int }}\left\{-\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+F\left(u(t)\right)\right\}\text{d}t$$

(3)

where T is the period of the oscillator ∂F/∂u = f(u).

In the functional (3), $-\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2$ is kinetic energy, and F(u(t)) is potential energy, so the functional (3) is the least Lagrangian action, from which we can immediately obtain its Hamiltonian, which reads:

$$H=\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+F\left(u(t)\right)=\text{constant}=H_0$$

(4)

or:

$$R(t)=\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+F(u(t))-F(A)$$

(5)

Equation (4) implies that the total energy keeps unchanged during the oscillation.

We use the following trial function to determine the angular frequency ω.

$$u(t)=Acos\mathit{\omega }t$$

(6)

where ω is the frequency. Submitting Eq. (6) into Eq. (5) results in a residual:

$$R(t)=\frac{1}{2}{A}^2{\mathit{\omega }}^2{sin}^2\mathit{\omega }t+F(Acos\mathit{\omega }t)-F(A)$$

(7)

If, by chance, the exact solution had been chosen as the trial function, then it would be possible to make R zero for all values of t by appropriate choice of ω. Since u(t) = A cos ωt is an approximation to the exact solution, R cannot be made zero everywhere. According to the energy balance method [2], locating at some a special point, that is, ωt = π/4 and setting R(t = π/4ω) = 0, we can obtain an approximate frequency–amplitude relationship of the studied nonlinear oscillator. Such treatment is much simple and has been widely used by engineers [3–7]. The accuracy of such location method, however, strongly depends upon the chosen location point. To overcome the shortcoming of the energy balance method, in this paper, we apply a new approach based on Hamiltonian [8, 9].

From Eq. (7), we have:

$$\frac{\mathit{\partial }H}{\mathit{\partial }A}=0.$$

(8)

Introducing a new function, $\overline{H}(u(t))$, defined as:

$$\overline{H}\left(u(t)\right)=\underset{0}{\overset{T/4}{\int }}\left\{\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+F\left(u(t)\right)\right\}\text{d}t=\frac{1}{4}TH$$

(9)

It is obvious that:

$$\frac{\mathit{\partial }\overline{H}}{\mathit{\partial }T}=\frac{1}{4}H$$

(10)

Equation (10) is, then, equivalent to the following one:

$$\frac{\mathit{\partial }}{\mathit{\partial }A}\left(\frac{\mathit{\partial }\overline{H}}{\mathit{\partial }T}\right)=0$$

(11)

or

$$\frac{\mathit{\partial }}{\mathit{\partial }A}\left(\frac{\mathit{\partial }\overline{H}}{\mathit{\partial }(1/\mathit{\omega })}\right)=0.$$

(12)

From Eq. (12), we can obtain approximate frequency–amplitude relationship of a nonlinear oscillators.

The application of Hamiltonian approach method for nonlinear dynamical systems

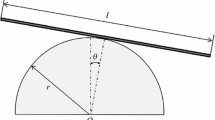
The motion of a rigid rod rocking back on the circular surface without slipping

In this section, we consider the motion of a rigid rod rocking back on the circular surface without slipping. The governing equation of this motion is in the following form [36]:

$$\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+\frac{3}{4}u{(t)}^2\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+\frac{3}{4}u(t){\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+3\frac{g}{l}u(t)cosu(t)=0$$

(13)

with the following initial conditions [36]:

$$u(0)=A,\frac{\text{d}}{\text{d}t}u(0)=0$$

(14)

where g and l are the positive constants. For this problem, we have:

$$f\left(u(t)\right)=\frac{3}{4}u{(t)}^2\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+\frac{3}{4}u(t){\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+3\frac{g}{l}u(t)cosu(t)$$

(15)

and:

$$F\left(u(t)\right)=\frac{3}{8}u{(t)}^2{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\frac{3g(cosu(t)+u(t)sinu(t))}{l}.$$

(16)

Its Hamiltonian can be easily obtained, which reads:

$$H=\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\frac{3}{8}u{(t)}^2{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\frac{3g(cosu(t)+u(t)sinu(t))}{l}.$$

(17)

Integrating Eq. (17) with respect to t from 0 to T/4, we have:

$$\overline{H}\left(u(t)\right)=\underset{0}{\overset{T/4}{\int }}\left\{\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\frac{3}{8}u{(t)}^2{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\frac{3g\left(cosu(t)+u(t)sinu(t)\right)}{l}\right\}\text{d}t.$$

(18)

Assuming that the solution can be expressed as u(t) = A cos ωt and substituting it to Eq. (18), we obtain:

$$\begin{array}{c}\overline{H}(u(t))=\underset{0}{\overset{T/4}{\int }}\left\{\begin{array}{c}\frac{1}{2}{A}^2{\mathit{\omega }}^2{sin}^2\mathit{\omega }t+\frac{3}{8}{A}^4{\mathit{\omega }}^2{cos}^2\mathit{\omega }t{sin}^2\mathit{\omega }t\\ +\frac{3g\left(cos(Acos\mathit{\omega }t)+Acos\mathit{\omega }t·sin(Acos\mathit{\omega }t)\right)}{l}\\ \end{array}\right\}\text{d}t\\ =\underset{0}{\overset{\mathit{\pi }/2}{\int }}\left\{\frac{1}{2}{A}^2\mathit{\omega }{sin}^{2}t+\frac{1}{\mathit{\omega }}\left[\begin{array}{c}\frac{3}{8}{A}^4{\mathit{\omega }}^2{cos}^{2}t{sin}^{2}t\\ +\frac{3g\left(cos(Acost)+Acost·sin(Acost)\right)}{l}\\ \end{array}\right]\right\}\\ =\frac{1}{2}{A}^2\mathit{\omega }·\frac{\mathit{\pi }}{4}+\frac{1}{\mathit{\omega }}\left[\frac{3}{8}{A}^4{\mathit{\omega }}^2·\frac{\mathit{\pi }}{16}+\frac{\mathit{\pi }}{2}·\frac{3g\left(\text{Bessel J(0,A) +}A·\text{Bessel J(1,A)}\right)}{l}\right].\\ \end{array}$$

(19)

In Eq. (19), we have two Bessel functions of the first kind. The Bessel functions are one of the special functions in mathematics. We can expand these Bessel functions of the first kind in the following form:

$$\text{Bessel J(0,}A)=1-\frac{1}{4}{A}^2+\frac{1}{64}{A}^4$$

(20)

and:

$$\text{Bessel J(1,}A)=\frac{1}{2}A-\frac{1}{16}{A}^3+\frac{1}{384}{A}^5$$

(21)

By substituting Eqs. (20) and (21) into Eq. (19), we obtain:

$$\overline{H}\left(u(t)\right)=\frac{1}{2}{A}^2\mathit{\omega }·\frac{\mathit{\pi }}{4}+\frac{1}{\mathit{\omega }}\left\{\frac{3}{8}{A}^4{\mathit{\omega }}^2·\frac{\mathit{\pi }}{16}+\frac{\mathit{\pi }}{2}·\frac{3g}{l}\left[\begin{array}{c}\left(1-\frac{1}{4}{A}^2+\frac{1}{64}{A}^4\right)\\ +A·\left(\frac{1}{2}A-\frac{1}{16}{A}^3+\frac{1}{384}{A}^5\right)\\ \end{array}\right]\right\}$$

(22)

Setting:

$$\frac{\mathit{\partial }}{\mathit{\partial }A}\left(\frac{\mathit{\partial }\overline{H}}{\mathit{\partial }(1/\mathit{\omega })}\right)=-A{\mathit{\omega }}^2·\frac{\mathit{\pi }}{4}-\frac{3}{8}{A}^3{\mathit{\omega }}^2·\frac{\mathit{\pi }}{4}+\frac{3g}{l}·\frac{\mathit{\pi }}{2}\left(-\frac{1}{2}A+\frac{1}{16}{A}^3+A-\frac{1}{4}{A}^3+\frac{1}{64}{A}^5\right)=0$$

(23)

We obtain the following frequency–amplitude relationship:

$${\mathit{\omega }}_{\text{HAM}}=\frac{\sqrt{\left(3g/l\right)\left(32+12A^2\right)\left(32-12A^2+A^4\right)}}{32+12A^2}.$$

(24)

Its period can be written in the following form:

$$T_{\text{HAM}}=\frac{2\mathit{\pi }}{\frac{\sqrt{\left(3g/l\right)\left(32+12A^2\right)\left(32-12A^2+A^4\right)}}{32+12A^2}}.$$

(25)

To illustrate the accuracy of the Hamiltonian approach method, we compare the approximate solution results with exact solution. For this dynamical system, the exact period is in the following form [36]:

$$T_{\text{Exact}}=4{\left(\frac{l}{3g}\right)}^{1/2}\underset{0}{\overset{\mathit{\pi }/2}{\int }}{\left(\frac{\left(4+3A^2{sin}^2\mathit{\phi }\right)A^2{cos}^2\mathit{\phi }}{8\left[AsinA+cosA-Asin\mathit{\phi }sin\left(Asin\mathit{\phi }\right)-cos\left(Asin\mathit{\phi }\right)\right]}\right)}^{1/2}\text{d}\mathit{\phi }.$$

(26)

A comparison of obtained results from the approximate period and the exact one is tabulated in Table 1 for g = 1.00, l = 1.00 and different values of A. From Table 1, the maximum relative error of the approximate periods is 1.9344 % for g = 1.00, l = 1.00 and A = 0.45π.

Table 1 Comparison of approximate periods with exact periods for g = 1.00, l = 1.00 and different values of A

Also, we present the comparison results of analytical approximate solution of u(t) based on t with exact solution with g = 1.00, l = 1.00 and different values of A in Figs. 1 and 2.

Fig. 1

Comparison of Hamiltonian approach method solution of u(t) based on t with exact solution for g = 1.00, l = 1.00, A = 0.05π

Fig. 2

Comparison of Hamiltonian approach method solution of u(t) based on t with exact solution for g = 1.00, l = 1.00, A = 0.45π

Also, to investigate on the behavior of this dynamical system, the effect of parameters g and l on the frequency corresponding to different values of amplitude (A) has been studied in Figs. 3 and 4.

Fig. 3

Comparison of frequency corresponding to different values of amplitude (A) and l = 1.00

Fig. 4

Comparison of frequency corresponding to different values of amplitude (A) and g = 1.00

The free vibrations of an autonomous conservative oscillator with inertia and static-type fifth-order nonlinearities

In this section, we consider the free vibrations of an autonomous conservative oscillator with inertia and static-type fifth-order nonlinearities. The differential equation of this dynamical system is the following form [37]:

$$\begin{array}{c}\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+{\mathit{\epsilon }}_{1}u{(t)}^2\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+{\mathit{\epsilon }}_{2}u{(t)}^4\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+{\mathit{\epsilon }}_{1}u(t){\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2\\ +2{\mathit{\epsilon }}_{2}u{(t)}^3{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\mathit{\lambda }u(t)+{\mathit{\epsilon }}_{3}u{(t)}^3+{\mathit{\epsilon }}_{4}u{(t)}^5=0,-1\le \mathit{\lambda }\le 1\\ \end{array}$$

(27)

with the following initial conditions [37]:

$$u(0)=A,\frac{\text{d}}{\text{d}t}u(0)=0$$

(28)

where ε₁, ε₂, ε₃ and ε₄ are positive parameters and λ is an integer which may take values of −1, 0 and 1 [37]. For this problem, we have:

$$\begin{array}{c}f\left(u(t)\right)={\mathit{\epsilon }}_{1}u{(t)}^2\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+{\mathit{\epsilon }}_{2}u{(t)}^4\left(\frac{{\text{d}}^2}{\text{d}{t}^2}u(t)\right)+{\mathit{\epsilon }}_{1}u(t){\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2\\ +2{\mathit{\epsilon }}_{2}u{(t)}^3{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\mathit{\lambda }u(t)+{\mathit{\epsilon }}_{3}u{(t)}^3+{\mathit{\epsilon }}_{4}u{(t)}^5\\ \end{array}$$

(29)

and:

$$\begin{array}{c}F\left(u(t)\right)=\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2{\mathit{\epsilon }}_{1}u{(t)}^2+\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2{\mathit{\epsilon }}_{2}u{(t)}^4\\ +\frac{1}{2}\mathit{\lambda }u{(t)}^2+\frac{1}{4}{\mathit{\epsilon }}_{3}u{(t)}^4+\frac{1}{6}{\mathit{\epsilon }}_{4}u{(t)}^6.\\ \end{array}$$

(30)

Its Hamiltonian can be easily obtained, which reads:

$$\begin{array}{c}H=\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2{\mathit{\epsilon }}_{1}u{(t)}^2+\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2{\mathit{\epsilon }}_{2}u{(t)}^4\\ +\frac{1}{2}\mathit{\lambda }u{(t)}^2+\frac{1}{4}{\mathit{\epsilon }}_{3}u{(t)}^4+\frac{1}{6}{\mathit{\epsilon }}_{4}u{(t)}^6.\\ \end{array}$$

(31)

Integrating Eq. (31) with respect to t from 0 to T/4, we have:

$$\overline{H}\left(u(t)\right)=\underset{0}{\overset{T/4}{\int }}\left\{\begin{array}{c}\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2+\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2{\mathit{\epsilon }}_{1}u{(t)}^2+\frac{1}{2}{\left(\frac{\text{d}}{\text{d}t}u(t)\right)}^2{\mathit{\epsilon }}_{2}u{(t)}^4\\ +\frac{1}{2}\mathit{\lambda }u{(t)}^2+\frac{1}{4}{\mathit{\epsilon }}_{3}u{(t)}^4+\frac{1}{6}{\mathit{\epsilon }}_{4}u{(t)}^6\\ \end{array}\right\}\text{d}t$$

(32)

Assuming that the solution can be expressed as u(t) = A cos ωt and substituting it to Eq. (32), we obtain:

$$\begin{array}{c}\overline{H}\left(u(t)\right)=\underset{0}{\overset{T/4}{\int }}\left\{\begin{array}{c}\frac{1}{2}{A}^2{\mathit{\omega }}^2{sin}^2\mathit{\omega }t+\frac{1}{2}{\mathit{\epsilon }}_1{A}^4{\mathit{\omega }}^2{sin}^2\mathit{\omega }t{cos}^2\mathit{\omega }t+\frac{1}{2}{\mathit{\epsilon }}_2{A}^6{\mathit{\omega }}^2{sin}^2\mathit{\omega }t{cos}^4\mathit{\omega }t\\ +\frac{1}{2}\mathit{\lambda }{A}^2{cos}^2\mathit{\omega }t+\frac{1}{4}{\mathit{\epsilon }}_3{A}^4{cos}^4\mathit{\omega }t+\frac{1}{6}{\mathit{\epsilon }}_4{A}^6{cos}^6\mathit{\omega }t\\ \end{array}\right\}\text{d}t\\ =\underset{0}{\overset{\mathit{\pi }/2}{\int }}\left\{\frac{1}{2}{A}^2\mathit{\omega }{sin}^{2}t+\frac{1}{\mathit{\omega }}\left[\begin{array}{c}\frac{1}{2}{\mathit{\epsilon }}_1{A}^4{\mathit{\omega }}^2{sin}^{2}t{cos}^{2}t+\frac{1}{2}{\mathit{\epsilon }}_2{A}^6{\mathit{\omega }}^2{sin}^{2}t{cos}^{4}t\\ +\frac{1}{2}\mathit{\lambda }{A}^2{cos}^{2}t+\frac{1}{4}{\mathit{\epsilon }}_3{A}^4{cos}^{4}t+\frac{1}{6}{\mathit{\epsilon }}_4{A}^6{cos}^{6}t\\ \end{array}\right]\right\}\text{d}t\\ =\frac{1}{2}{A}^2\mathit{\omega }·\frac{\mathit{\pi }}{4}+\frac{1}{\mathit{\omega }}\left[\begin{array}{c}\frac{1}{2}{\mathit{\epsilon }}_1{A}^4{\mathit{\omega }}^2·\frac{\mathit{\pi }}{16}+\frac{1}{2}{\mathit{\epsilon }}_2{A}^6{\mathit{\omega }}^2·\frac{\mathit{\pi }}{32}+\frac{1}{2}\mathit{\lambda }{A}^2·\frac{\mathit{\pi }}{4}\\ +\frac{1}{4}{\mathit{\epsilon }}_3{A}^4·\frac{3\mathit{\pi }}{16}+\frac{1}{6}{\mathit{\epsilon }}_4{A}^6·\frac{5\mathit{\pi }}{32}\\ \end{array}\right].\\ \end{array}$$

(33)

Setting:

$$\begin{array}{c}\frac{\mathit{\partial }}{\mathit{\partial }A}\left(\frac{\mathit{\partial }\overline{H}}{\mathit{\partial }(1/\mathit{\omega })}\right)=-A{\mathit{\omega }}^2·\frac{\mathit{\pi }}{4}-2{\mathit{\epsilon }}_1{A}^3{\mathit{\omega }}^2·\frac{\mathit{\pi }}{16}-3{\mathit{\epsilon }}_2{A}^5{\mathit{\omega }}^2·\frac{\mathit{\pi }}{32}\\ +\mathit{\lambda }A·\frac{\mathit{\pi }}{4}+{\mathit{\epsilon }}_3{A}^3·\frac{3\mathit{\pi }}{16}+{\mathit{\epsilon }}_4{A}^5·\frac{5\mathit{\pi }}{32}=0.\\ \end{array}$$

(34)

We obtain the following frequency–amplitude relationship:

$${\mathit{\omega }}_{\text{HAM}}=\sqrt{\frac{6{\mathit{\epsilon }}_3{A}^2+5{\mathit{\epsilon }}_4{A}^4+8\mathit{\lambda }}{8+4{\mathit{\epsilon }}_1{A}^2+3{\mathit{\epsilon }}_2{A}^4}}$$

(35)

Its period can be written in the following form:

$$T_{\text{HAM}}=\frac{2\mathit{\pi }}{\sqrt{\frac{6{\mathit{\epsilon }}_3{A}^2+5{\mathit{\epsilon }}_4{A}^4+8\mathit{\lambda }}{8+4{\mathit{\epsilon }}_1{A}^2+3{\mathit{\epsilon }}_2{A}^4}}}$$

(36)

For this dynamical system, because there is no exact solution, we compare the approximate solution results with Runge–Kutta method, as one of the known numerical methods. The numerical solution with Runge–Kutta method for this nonlinear differential equation is:

$$\frac{\text{d}}{\text{d}t}{u}_1(t)=u_2(t),{\text{u}}_1(0)=A$$

(37)

and

$$\frac{\text{d}}{\text{d}t}{u}_2(t)=-\frac{1}{1+{\mathit{\epsilon }}_1{u}_1{(t)}^2+{\mathit{\epsilon }}_2{u}_1{(t)}^4}\left(\begin{array}{c}\mathit{\lambda }{u}_1(t)+{\mathit{\epsilon }}_1{u}_1(t)u_2{(t)}^2\\ +2{\mathit{\epsilon }}_2{u}_1{(t)}^3{u}_2{(t)}^2\\ +{\mathit{\epsilon }}_3{u}_1{(t)}^3+{\mathit{\epsilon }}_4{u}_1{(t)}^5\\ \end{array}\right).$$

(38)

Motion is assumed to start from the position of maximum displacement with zero initial velocity. λ is an integer which may take values of −1, 0 and 1, and ε₁, ε₂, ε₃ and ε₄ are positive parameters. The values of parameters ε₁, ε₂, ε₃ and ε₄ associated for a mode are shown in Table 2.

Table 2 Values of dimensionless parameters ε _i for a mode

To illustrate the accuracy of the Hamiltonian approach method solution, we present the comparison results of analytical approximate solution of u(t) based on t with the numerical solution which solved by Runge–Kutta method as one of the known numerical methods in Figs. 5 and 6 for λ = 1.00, A = 1.00 and various modes (mode-1 and mode-3).

Fig. 5

Comparison of Hamiltonian approach method solution of u(t) based on t with numerical solution (Runge–Kutta method) for λ = 1.00, A = 1.00in mode-1

Fig. 6

Comparison of Hamiltonian approach method solution of u(t) based on t with numerical solution (Runge–Kutta method) for λ = 1.00, A = 1.00 in mode-3

Figures 7 and 8 present the high accuracy of Hamiltonian approach method solution in comparison with numerical solution for different values of ε₁, ε₂, ε₃ and ε₄, and show the phase–space curves (du/dt versus u(t) curve) for amplitude A = 1.00 and λ = 1.00.

Fig. 7

Comparison of analytical approximate solution of du/dt based on u(t) with the with numerical solution (Runge–Kutta method) for λ = 1.00, A = 1.00 in mode-1

Fig. 8

Comparison of analytical approximate solution of du/dt based on u(t) with the with numerical solution (Runge–Kutta method) for λ = 1.00, A = 1.00 in mode-3

It can be observed that the phase–space curves generated from approximate solution are close to that of the numerical curves. The phase plots show the behavior of the dynamical system in modes 1 and 3. It is periodic with a center at (0, 0).

Also, to investigate on the behavior of this dynamical system, the effect of parameters ε₁, ε₂, ε₃ and ε₄ on the frequency corresponding to different values of amplitude (A) has been studied in Fig. 9.

Fig. 9

Comparison of frequency corresponding to different values of amplitude (A) and various modes, mode-1, mode-2 and mode-3

It is evident that Hamiltonian approach method shows excellent agreement with the exact and numerical solutions and is quickly convergent and valid for a wide range of vibration amplitudes and initial conditions. The accuracy of the results shows that the Hamiltonian approach method can be potentiality used for the analysis of strongly nonlinear oscillation problems accurately.

Conclusion

In this article, we applied Hamiltonian approach method as one of the analytical approximate techniques, for studying the strongly nonlinear dynamical systems such as the motion of a rigid rod rocking back on the circular surface without slipping and the free vibrations of an autonomous conservative oscillator with inertia and static-type fifth-order nonlinearities.

Comparison of the results which are obtained by this method with the obtained result by the exact and numerical solutions reveal that the Hamiltonian approach method is very effective and convenient and does not require linearization or small perturbation and can be easily extended to other nonlinear dynamical systems and can therefore be found widely applicable in engineering and other sciences.

Authors contributions

MH conceived the study and participated in its design and coordination. MS carried out the numerical solution of equations and participated in drafting the manuscript. HEK carried out the software work and the solution of equations using analytical approximate methods. All authors read and approved the final manuscript.