Abstract
The concept of derivative is a basic concept of calculus. It is closely related to the concept of function, the idea of rate of change, and the limit concept. In recent decades, teaching the concept of derivative in mathematics classrooms has changed: a quite formal approach—closely linked to the teaching of calculus at university and based on the sequence concept—has been transformed to or substituted by a new one. This means working with rates of change, an intuitive access to the concepts of limit and derivative. It includes working with real functions right from the beginning, a great emphasis on graphs, and the use of digital technologies. The meaning of sequences has decreased to a point where they are sometimes no longer even taught in the calculus course. In recent years this concept has been criticized for not developing adequate perceptions of the basic concepts of calculus and not sufficiently preparing the students for scientific courses at university. In this paper we present an alternative discrete step-by-step approach to the basic concepts of calculus by working with sequences and difference sequences, functions defined on \( \mathbb{Z}\) and discrete domains of \( \mathbb{Q}\), and by subsequently developing the concept of rate of change in a discrete learning environment. The paper is based on general theoretical considerations and empirical investigations by the author and is meant as a contribution to classroom design-research or “design science” (Wittmann, Educ Stud Math 29(4):355–374, 1995).

















Similar content being viewed by others
Notes
In this paper we emphasize the access to the concept of derivative in coming from the average to the local rate of change of a function. We do not consider the alternative concept of the local linearization of a function.
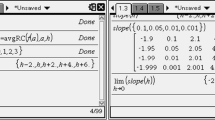
We used the program ScreenCam: http://en.wikipedia.org/wiki/Screencam (Accessed 1 May 2014).
The difference sequence and hence the graph do not change.
References
Artin, E. (1957). A freshman honors course in calculus and analytic geometry. Taught at Princeton University. Charlottesville, Virginia: Mathematical Association of America.
Bauer, L. (2011). Mathematics, intuition, formalization,: a study of students’ conceptions of 0.9999…. [Mathematik, Intuition, Formalisierung: eine Untersuchung von Schülerinnen- und Schülervorstellungen zu 0,9999….]. Journal für Mathematik-Didaktik, 32(1), 79–102.
Blum, W. (1975). Ein Grundkurs in analysis. Didaktik der Mathematik, 3, 163–184.
Büyükköroglu, T., Düzce, S. A., Çetin, N., Mahir, N., Deniz, A., & Üreyen, M. (2006). The effect of computers on teaching the limit concept. International Journal for Mathematics Teaching and Learning, 03.05. Published online. http://www.cimt.plymouth.ac.uk/journal. Accessed 5 May 2014.
Caballero-Gonzalez, C., & Bernal-Rodriguez, J. (2011). New technologies and education: Constructive, geometric and dynamic introduction of the derivative concept. International Journal for Technology in Mathematics Education, 18(4), 203–208.
Çetin, N. (2009). The performance of undergraduate students in the limit concept. International Journal of Education in Mathematics, Science and Technology, 40(3), 323–330.
Churchman, F. L. (1972). A comparative study of three different approaches to the limit concept. Dissertation. University of Georgia.
Crouch, R., & Haines, C. (2004). Mathematical modelling: transitions between the real world and the mathematical model. International Journal of Education in Mathematics, Science and Technology, 35(2), 197–206.
Doorman, M., & Gravemeijer, K. (2009). Emergent modelling: discrete graphs to support the understanding of change and velocity. ZDM—The International Journal on Mathematics Education, 41, 199–211.
Drijvers, P., & Trouche, L. (2008). From artefacts to instruments: a theoretical framework behind the orchestra metaphor. In G. W. Blume & M. K. Heid (Eds.), Research on technology and the teaching and learning of mathematics (Vol. 2, pp. 363–392)., Cases and perspectives Charlotte, NC: Information Age.
Ellis, R., & Gulick, D. (1989/2003). HBJ calculus (with Analytic geometry). Orlando, FL: Harcourt Brace Jovanovich.
Freudenthal, H. (1983). Didactical phenomenology of mathematical structure. Dordrecht: Reidel.
Gordon, S. P. (1979). A discrete approach to the calculus. International Journal of Education in Mathematics, Science and Technology, 10(1), 21–31.
Gravemeijer, K., & Doorman, M. (1999). Context problems in realistic mathematics education: A calculus course as an example. Educational Studies in Mathematics, 39, 111–129.
Gray, E., & Tall, D. (1994). Duality, ambiguity, and flexibility: A “proceptual” view of simple arithmetic. Journal for Research in Mathematics Education, 25(2), 116–140.
Hahn, S., & Prediger, S. (2008). Amount and change—a contribution to the didactic reconstruction of calculus [Bestand und Änderung—Ein Beitrag zur didaktischen Rekonstruktion der Analysis]. Journal für Mathematik-Didaktik, 29(3/4), 163–198.
Henning, A., & Hoffkamp, A. (2013). Developing an intuitive concept of limit when approaching the derivative function. Proceedings of CERME 8. Antalya, Turkey.
Kidron, I., & Zehavi, N. (2002). The role of animation in teaching the limit concept. International Journal of Computer Algebra in Mathematics Education, 9(3), 205–227.
Lang, S. (1964/1973). A first course in calculus. Dordrecht: Springer.
Larson, R. E., & Hostetler, R. P. (1986/2009). Calculus (with analytic geometry). Lexington, MA, and Toronto: Heath.
Mamona-Downs, J. (2001). Letting the intuitive bear on the formal: A didactical approach for the understanding of the limit of a sequence. Educational Studies in Mathematics, 48(2–3), 259–288.
Martinovic, D., & Karadag, Z. (2012). Dynamic and interactive mathematics learning environments: The case of teaching the limit concept. Teaching Mathematics and its Applications: An International Journal of the IMA, 31(1), 41–48.
NCTM. (1989). Standards for School Mathematics. Reston, VA: National Council of Teachers of Mathematics.
NCTM. (2000). Principles and Standards for School Mathematics. Reston, VA: National Council of Teachers of Mathematics.
Penuel, W. R., Fishman, B. J., Cheng, B., & Sabellin, N. (2011). Organizing research and development at the intersection of learning, implementation, and design. Educational Researcher, 40(7), 331–337.
Posner, G. J., Strike, K. A., Hewson, P. W., & Gertzog, W. A. (1982). Accommodation of a scientific conception: Toward a theory of conceptual change. Science Education, 66(2), 211–227.
Quesada, A., Einsporn, R. L., & Wiggins, M. (2008). The impact of the graphical approach on students’ understanding of the formal definition of limit. International Journal for Technology in Mathematics Education, 15(3), 95–102.
Ralston, A., & Young, G. S. (1983). The future of college mathematics. New York: Springer.
Robert, A. (1981). L’acquisition du concept de convergence des suites numéri-ques dans l’enseignement supérieur. Bull. Assoc. Prof. Math. Enseign. Public (pp. 649–674).
Roh, K. H. (2008). Students’ images and their understanding of definitions of the limit of a sequence. Educational Studies in Mathematics, 69(3), 217–233.
Roorda, G., Vos, P., & Goedhart, M. (2007). The concept of the derivative in modelling and applications. In Chr. Haines et al. (Eds.), Mathematical modelling (ICTMA 12): Education, engineering and economics. Proceedings of the 12th international conference on the teaching of mathematical modelling and applications, London, UK, July 10–14, 2005. Chichester: Horwood.
Seidman, S. B., & Rice, M. D. (1986). A fundamental course in higher mathematics incorporating discrete and continuous themes. In R. F. Churchhouse (Ed.), The influence of computers and informatics on mathematics and its teaching (pp. 95–106). Cambridge: Cambridge University Press.
Sierpinska, A. (1987). Humanities students and epistemological obstacles related to limits. Educational Studies in Mathematics, 18, 371–397.
Swinyard, C. (2011). Reinventing the formal definition of limit: The case of Amy and Mike. Journal of Mathematical Behavior, 30(2), 93–114.
Swinyard, C., & Larsen, S. (2012). Coming to understand the formal definition of limit: Insights gained from engaging students in reinvention. Journal for Research in Mathematics Education, 43(4), 465–493.
Tall, D. (1977). Conflicts and catastrophes in the learning of mathematics. Mathematical Education for Teaching, 2(4), 3–18.
Tall, D. (1992). The transition to advanced mathematical thinking: functions, limits, infinity, and proof. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 495–511). New York: Macmillan.
Tall, D. (1993). Students’ difficulties in calculus. Proceedings of Working Group 3 on Students’ Difficulties in Calculus, ICME-7 1992 (pp. 13–28). Québec, Canada.
Tall, D. (2013). How humans learn to think mathematically: Exploring the three worlds of mathematics (learning in doing: social, cognitive and computational perspectives). Cambridge: Cambridge University Press.
Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151–169.
Thies, S., & Weigand, H.-G. (2003). Working styles of students in a computer-based environment—results of a DFG project. In G. Törner et al. (Eds.), Selected papers from the Annual Conferences on Didactics of Mathematics, Ludwigsburg 2001. Hildesheim: Franzbecker. http://webdoc.sub.gwdg.de/ebook/e/gdm/2001/index.html. Accessed 5 May 2014.
Volkert, K. (1988). Geschichte der analysis. Mannheim: Wissenschafts Verlag.
Vollrath, H.-J. (1994). Methodik des Begriffslehrens. Stuttgart: Klett.
Weigand, H.-G. (2004). Sequences—basic elements for discrete mathematics. ZDM—Zentralblatt für Didaktik der Mathematik, 36(3), 91–97.
Wittmann, E. Chr. (1995). Mathematics education as a “design science”. Educational Studies in Mathematics, 29(4), 355–374.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Weigand, HG. A discrete approach to the concept of derivative. ZDM Mathematics Education 46, 603–619 (2014). https://doi.org/10.1007/s11858-014-0595-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-014-0595-x