Skip to main content

Advertisement

SpringerLink
Log in

Decomposition of Neurological Multivariate Time Series by State Space Modelling

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

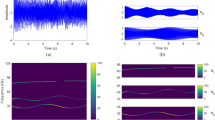
Decomposition of multivariate time series data into independent source components forms an important part of preprocessing and analysis of time-resolved data in neuroscience. We briefly review the available tools for this purpose, such as Factor Analysis (FA) and Independent Component Analysis (ICA), then we show how linear state space modelling, a methodology from statistical time series analysis, can be employed for the same purpose. State space modelling, a generalization of classical ARMA modelling, is well suited for exploiting the dynamical information encoded in the temporal ordering of time series data, while this information remains inaccessible to FA and most ICA algorithms. As a result, much more detailed decompositions become possible, and both components with sharp power spectrum, such as alpha components, sinusoidal artifacts, or sleep spindles, and with broad power spectrum, such as FMRI scanner artifacts or epileptic spiking components, can be separated, even in the absence of prior information. In addition, three generalizations are discussed, the first relaxing the independence assumption, the second introducing non-stationarity of the covariance of the noise driving the dynamics, and the third allowing for non-Gaussianity of the data through a non-linear observation function. Three application examples are presented, one electrocardigram time series and two electroencephalogram (EEG) time series. The two EEG examples, both from epilepsy patients, demonstrate the separation and removal of various artifacts, including hum noise and FMRI scanner artifacts, and the identification of sleep spindles, epileptic foci, and spiking components. Decompositions obtained by two ICA algorithms are shown for comparison.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Aït-Sahalia, Y., & Kimmel, R. (2007). Maximum likelihood estimation of stochastic volatility models. J. Financ. Econ., 83, 413–452.

    Article  Google Scholar 

  • Akaike, H. (1974a). Markovian representation of stochastic processes and its application to the analysis of autoregressive moving average processes. Ann. Inst. Stat. Math., 26, 363–387.

    Article  MathSciNet  MATH  Google Scholar 

  • Akaike, H. (1974b). A new look at the statistical model identification. IEEE Trans. Autom. Control, 19, 716–723.

    Article  MathSciNet  MATH  Google Scholar 

  • Akaike, H., & Nakagawa, T. (1988). Statistical analysis and control of dynamic systems. Dordrecht: Kluwer Academic.

    MATH  Google Scholar 

  • Allen, P. J., Josephs, O., & Turner, R. (2000). A method for removing imaging artifact from continuous EEG recorded during functional MRI. NeuroImage, 12, 230–239.

    Article  Google Scholar 

  • Åström, K. J. (1980). Maximum likelihood and prediction error methods. Automatica, 16, 551–574.

    Article  MATH  Google Scholar 

  • Attias, H., & Schreiner, C. E. (1998). Blind source separation and deconvolution: the dynamic component analysis algorithm. Neural Comput., 10, 1373–1424.

    Article  Google Scholar 

  • Baldick, R. (Ed.) (2006). Applied optimization: formulation and algorithms for engineering systems. Cambridge: Cambridge University Press.

    MATH  Google Scholar 

  • Bar-Shalom, Y., & Fortmann, T. (1988). Tracking and data association. San Diego: Academic Press.

    MATH  Google Scholar 

  • Barros, A. K., & Cichocki, A. (2001). Extraction of specific signals with temporal structure. Neural Comput., 13, 1995–2000.

    Article  Google Scholar 

  • Basilevsky, A. (1994). Statistical factor analysis and related methods: theory and applications. New York: Wiley-Interscience.

    Book  MATH  Google Scholar 

  • Beckmann, C., & Smith, S. (2004). Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans. Med. Imaging, 23, 137–152.

    Article  Google Scholar 

  • Beckmann, C., & Smith, S. (2005). Tensorial extensions of independent component analysis for multisubject FMRI analysis. NeuroImage, 25, 294–311.

    Article  Google Scholar 

  • Belouchrani, A., Abed-Meraim, K., Cardoso, J.-F., & Moulines, E. (1997). A blind source separation technique using second order statistics. IEEE Trans. Signal Process., 45, 434–444.

    Article  Google Scholar 

  • Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. J. Econom., 31, 307–327.

    Article  MathSciNet  MATH  Google Scholar 

  • Box, G. E. P., & Jenkins, G. M. (1970). Time series analysis, forecasting and control. San Francisco: Holden-Day.

    MATH  Google Scholar 

  • Brockwell, P. J., & Davis, R. A. (1987). Time series: theory and methods. Berlin: Springer.

    MATH  Google Scholar 

  • Cheung, Y. M., & Xu, L. (2003). Dual multivariate auto-regressive modeling in state space for temporal signal separation. IEEE Trans. Syst. Man Cybern., 33, 386–398.

    Google Scholar 

  • Choi, S., Cichocki, A., Park, H., & Lee, S. (2005). Blind source separation and independent component analysis: a review. Neural Inf. Process. Lett. Rev., 6, 1–57.

    Google Scholar 

  • Chui, C. K., & Chen, G. (1999). Springer series in information sciences : Vol. 17. Kalman filtering: with real-time applications (3rd ed.). Berlin: Springer.

    Google Scholar 

  • Cichocki, A., & Amari, S. (2002). Adaptive blind signal and image processing. Chichester: Wiley.

    Book  Google Scholar 

  • Comon, P. (1994). Independent component analysis, a new concept? Signal Process., 36, 287–314.

    Article  MATH  Google Scholar 

  • Delorme, A., Sejnowski, T., & Makeig, S. (2007). Enhanced detection of artifacts in EEG data using higher-order statistics and independent component analysis. NeuroImage, 34, 1443–1449.

    Article  Google Scholar 

  • Durbin, J., & Koopman, S. J. (2001). Time series analysis by state space methods. Oxford: Oxford University Press.

    MATH  Google Scholar 

  • Dyrholm, M., Makeig, S., & Hansen, L. K. (2007). Model selection for convolutive ICA with an application to spatiotemporal analysis of EEG. Neural Comput., 19, 934–955.

    Article  MATH  Google Scholar 

  • Engle, R. F., & Watson, M. (1981). A one-factor multivariate time series model of metropolitan wage rates. J. Am. Stat. Assoc., 76, 774–781.

    Article  Google Scholar 

  • Galka, A., Yamashita, O., & Ozaki, T. (2004). GARCH modelling of covariance in dynamical estimation of inverse solutions. Phys. Lett. A, 333, 261–268.

    Article  MATH  Google Scholar 

  • Galka, A., Ozaki, T., Bosch-Bayard, J., & Yamashita, O. (2006). Whitening as a tool for estimating mutual information in spatiotemporal data sets. J. Stat. Phys., 124, 1275–1315.

    Article  MathSciNet  MATH  Google Scholar 

  • Galka, A., Wong, K., & Ozaki, T. (2010). Generalized state space models for modeling non-stationary EEG time series. In A. Steyn-Ross & M. Steyn-Ross (Eds.), Springer series in computational neuroscience. Modeling phase transitions in the brain (pp. 27–52). Berlin: Springer.

    Chapter  Google Scholar 

  • Gevers, M. (2006). A personal view of the development of system identification. IEEE Control Syst. Mag., 26, 93–105.

    Article  Google Scholar 

  • Gnedenko, B. V. (1969). The theory of probability. Moscow: Mir Publishers.

    MATH  Google Scholar 

  • Grewal, M. S., & Andrews, A. P. (2001). Kalman filtering: theory and practice using MATLAB. New York: Wiley-Interscience.

    Google Scholar 

  • Harman, H. H. (1976). Modern factor analysis (3rd ed.). Chicago: University of Chicago Press.

    Google Scholar 

  • Harvey, A., Koopman, S. J., & Shephard, N. (Eds.) (2004). State space and unobserved component models. Cambridge: Cambridge University Press.

    MATH  Google Scholar 

  • Hyvärinen, A. (1999). Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw., 10, 626–634.

    Article  Google Scholar 

  • Hyvärinen, A., Karhunen, J., & Oja, E. (2001). Independent component analysis. New York: Wiley.

    Book  Google Scholar 

  • James, C., & Hesse, C. (2005). Independent component analysis for biomedical signals. Physiol. Meas., 26, R15–R39.

    Article  Google Scholar 

  • Jung, A., & Kaiser, A. (2003). Considering temporal structures in independent component analysis. In: Proc. 4th int. symp. ICA BSS, ICA 2003 (pp. 95–100). Nara, Japan, Apr. 2003.

  • Jung, T.-P., Makeig, S., McKeown, M., Bell, A., Lee, T.-W., & Sejnowski, T. (2001). Imaging brain dynamics using independent component analysis. IEEE Proc., 88, 1107–1122.

    Article  Google Scholar 

  • Kailath, T. (1968). An innovations approach to least-squares estimation—Part I: linear filtering in additive white noise. IEEE Trans. Autom. Control, 13, 646–655.

    Article  MathSciNet  Google Scholar 

  • Kailath, T. (1980). Information and system sciences series. Linear systems. Englewood Cliffs: Prentice-Hall.

    MATH  Google Scholar 

  • Kallenberg, O. (2002). Foundations of modern probability. Berlin: Springer.

    MATH  Google Scholar 

  • Kalman, R. E. (1960). A new approach to linear filtering and prediction problems. J. Basic Eng., 82, 35–45.

    Google Scholar 

  • Kalman, R. E., Falb, P. L., & Arbib, M. A. (1969). International series in pure and applied mathematics. Topics in mathematical system theory. New York: McGraw-Hill.

    MATH  Google Scholar 

  • Ljung, L. (1999). System identification: theory for the user (2nd ed.). Englewood Cliffs: Prentice-Hall.

    Google Scholar 

  • Mehra, R. K. (1971). Identification of stochastic linear systems using Kalman filter representation. AIAA J., 9, 28–31.

    Article  MATH  Google Scholar 

  • Mehra, R. K. (1974). Identification in control and econometrics: similarities and differences. Ann. Econ. Soc. Meas., 3, 21–47.

    Google Scholar 

  • Meinecke, F., Ziehe, A., Kawanabe, M., & Müller, K.-R. (2002). A resampling approach to estimate the stability of one- or multidimensional independent components. IEEE Trans. Biomed. Eng., 49, 1514–1525.

    Article  Google Scholar 

  • Miwakeichi, F., Martínez-Montes, E., Valdés-Sosa, P., Nishiyama, N., Mizuhara, H., & Yamaguchi, Y. (2004). Decomposing EEG data into space-time-frequency components using parallel factor analysis. NeuroImage, 22, 1035–1045.

    Article  Google Scholar 

  • Molenaar, P. C. (1985). A dynamic factor model for the analysis of multivariate time series. Psychometrika, 50, 181–202.

    Article  MATH  Google Scholar 

  • Molgedey, L., & Schuster, H. G. (1994). Separation of a mixture of independent signals using time delayed correlations. Phys. Rev. Lett., 72, 3634–3637.

    Article  Google Scholar 

  • Negishi, M., Abildgaard, M., Nixon, T., & Constable, R. (2004). Removal of time-varying gradient artifacts from EEG data acquired during continuous fMRI. Clin. Neurophysiol., 115, 2181–2192.

    Article  Google Scholar 

  • Neumaier, A., & Schneider, T. (2001). Estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Trans. Math. Softw., 27, 27–57.

    Article  MATH  Google Scholar 

  • Niazy, R., Beckmann, C., Iannetti, D., Brady, J., & Smith, S. (2005). Removal of FMRI environment artifacts from EEG data using optimal basis sets. NeuroImage, 28, 720–737.

    Article  Google Scholar 

  • Otter, P. (1986). Dynamic structural systems under indirect observation: identifiability and estimation aspects from a system theoretic perspective. Psychometrika, 51, 415–428.

    Article  MathSciNet  MATH  Google Scholar 

  • Ozaki, T., & Iino, M. (2001). An innovation approach to non-Gaussian time series analysis. J. Appl. Probab., 38, 78–92.

    Article  MathSciNet  Google Scholar 

  • Pagan, A. R. (1975). A note on the extraction of components from time series. Econometrica, 43, 163–168.

    Article  MATH  Google Scholar 

  • Pearlmutter, B. A., & Parra, L. C. (1997). Maximum likelihood blind source separation: a context-sensitive generalization of ICA. In M. C. Mozer, M. I. Jordan & T. Petsche (Eds.), Advances in neural information processing systems (Vol. 9, pp. 613–619). Cambridge: MIT Press.

    Google Scholar 

  • Protter, P. (1990). Stochastic integration and differential equations. Berlin: Springer.

    MATH  Google Scholar 

  • Rauch, H. E., Tung, G., & Striebel, C. T. (1965). Maximum likelihood estimates of linear dynamic systems. AIAA J., 3, 1445–1450.

    Article  MathSciNet  Google Scholar 

  • Schwarz, G. (1978). Estimating the dimension of a model. Ann. Stat., 6, 461–464.

    Article  MATH  Google Scholar 

  • Schweppe, F. (1965). Evaluation of likelihood functions for Gaussian signals. IEEE Trans. Inf. Theory, 11, 61–70.

    Article  MathSciNet  MATH  Google Scholar 

  • Sorenson, H. W. (1970). Least-squares estimation: from Gauss to Kalman. IEEE Spectr., 7, 63–68.

    Article  Google Scholar 

  • Stögbauer, H., Kraskov, A., Astakhov, S. A., & Grassberger, P. (2004). Least-dependent-component analysis based on mutual information. Phys. Rev. E, 70, 066123.

    Article  Google Scholar 

  • Tong, L., Liu, R., Soon, V. C., & Huang, Y. (1991). Indeterminacy and identifiability of blind separation. IEEE Trans. Circuits Syst., 38, 499–509.

    Article  MATH  Google Scholar 

  • Vigário, R., Sarela, J., Jousmiki, V., Hamalainen, M., & Oja, E. (2000). Independent component approach to the analysis of EEG and MEG recordings. IEEE Trans. Biomed. Eng., 47, 589–593.

    Article  Google Scholar 

  • Waheed, K., & Salem, F. M. (2005). Linear state space feedforward and feedback structures for blind source recovery in dynamic environments. Neural Process. Lett., 22, 325–344.

    Article  Google Scholar 

  • Wong, K. F. K., Galka, A., Yamashita, O., & Ozaki, T. (2006). Modelling non-stationary variance in EEG time series by state space GARCH model. Comput. Biol. Med., 36, 1327–1335.

    Article  Google Scholar 

  • Zhang, L., & Cichocki, A. (2000). Blind deconvolution of dynamical systems: a state space approach. J. Signal Process., 4, 111–130.

    Google Scholar 

  • Ziehe, A., & Müller, K.-R. (1998). TDSEP—an efficient algorithm for blind separation using time structure. In L. Niklasson, M. Bodén & T. Ziemke (Eds.), Proc. 8th int. conf. artificial neural networks, ICANN’98 (pp. 675–680). Berlin: Springer.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Neuropediatrics, University of Kiel, 24098, Kiel, Germany

    Andreas Galka, Hiltrud Muhle, Ulrich Stephani & Michael Siniatchkin

  2. Institute of Experimental and Applied Physics, University of Kiel, 24098, Kiel, Germany

    Andreas Galka

  3. Information and Coding Theory Lab, Faculty of Engineering, University of Kiel, 24098, Kiel, Germany

    Andreas Galka

  4. Massachusetts General Hospital, Harvard Medical School, Boston, MA, 02114, USA

    Kin Foon Kevin Wong

  5. Tohoku University, 28 Kawauchi, Aoba-ku, Sendai, 980-8576, Japan

    Tohru Ozaki

Authors
  1. Andreas Galka
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kin Foon Kevin Wong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tohru Ozaki
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hiltrud Muhle
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ulrich Stephani
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Michael Siniatchkin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Andreas Galka.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Galka, A., Wong, K.F.K., Ozaki, T. et al. Decomposition of Neurological Multivariate Time Series by State Space Modelling. Bull Math Biol 73, 285–324 (2011). https://doi.org/10.1007/s11538-010-9563-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11538-010-9563-y

Keywords

Search

Navigation