Skip to main content
SpringerLink
Log in

Non-Uniform Doo-Sabin Subdivision Surface via Eigen Polygon

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

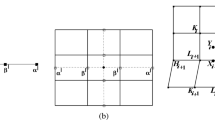
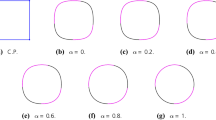
This paper constructs a new non-uniform Doo-Sabin subdivision scheme via eigen polygon. The authors proved that the limit surface is always convergent and is G1 continuous for any valence and any positive knot intervals under a minor assumption, that λ is the second and third eigenvalues of the subdivision matrix. And then, a million of numerical experiments are tested with randomly selecting positive knot intervals, which verify that our new subdivision scheme satisfies the assumption. However this is not true for the other two existing non-uniform Doo-Sabin schemes in [32, 33]. In additional, numerical experiments indicate that the quality of the new limit surface can be improved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Warren J and Weimer H, Subdivision Methods for Geometric Design, Morgan, Kaufmann, 2002.

  2. Muller K, Reusche L, and Fellner D, Extended subdivision surfaces: Building a bridge between NURBS and Catmull-Clark surfaces, ACM Transactions on Graphics, 2006, 25: 268–292.

    Article  Google Scholar 

  3. Doo D and Sabin M, Behaviour of recursive division surfaces near extraordinary points, Computer Aided Design, 1978, 10: 356–360.

    Article  Google Scholar 

  4. Catmull E and Clark J, Recursively generated B-spline surfaces on arbitrary topological meshes, Computer Aided Design, 1978, 10: 350–355.

    Article  Google Scholar 

  5. Loop C, Smooth subdivision surfaces based on triangles, Master’s thesis, University of Utah, 1987.

  6. Kobbelt L, \(\sqrt 3 \)-subdivision, SIGGRAPH’ 00: Proceedings of the 27th annual conference on Computer graphics and interactive techniques, ACM Press/Addison-Wesley Publishing Co., 2000, 103–112.

  7. Velho L and Zorin D, Quasi 4–8 subdivision, Computer Aided Geometric Design, 2001, 18: 345–358.

    Article  MathSciNet  Google Scholar 

  8. Velho L and Zorin D, 4–8 subdivision, Computer Aided Geometric Design, 2001, 18: 397–427.

    Article  MathSciNet  Google Scholar 

  9. Stam J and Loop C, Quad/Triangle subdivision, Computer Graphics Forum, 2003, 22: 1–7.

    Article  Google Scholar 

  10. Peters J and Shiue L, Combining 4- and 3-direction subdivision, ACM Transactions on Graphics, 2004, 23: 980–1003.

    Article  Google Scholar 

  11. Dyn N, Levin D, and Gregory J A, A four-point interpolatory subdivision scheme for curve design, Computer Aided Geometric Design, 1987, 4: 257–268.

    Article  MathSciNet  Google Scholar 

  12. Dyn N and Levin D, A butterfly subdivision scheme for surface interpolation with tension control, ACM Transactions on Graphics, 1990, 9: 160–169.

    Article  Google Scholar 

  13. Zorin D, Schröder P, and Sweldens W, Interpolating Subdivision for meshes with arbitrary topology, SIGGRAPH’96: Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, ACM, New York, NY, USA, 1996, 189–192.

  14. Kobbelt L, Interpolatory subdivision on open quadrilateral nets with arbitrary topology, Computer Graphics Forum, 1996, 15: 400–410.

    Article  Google Scholar 

  15. Deng C and Ma W, A unified interpolatory subdivision scheme for quadrilateral meshes, ACM Transactions on Graphics, 2013, 32(3): 1–11.

    Article  Google Scholar 

  16. Li X and Zheng J, An alternative method for constructing interpolatory subdivision from approximating subdivision, Computer Aided Geometric Design, 2012, 29(4): 474–484.

    Article  MathSciNet  Google Scholar 

  17. Labsik U and Greiner G, Interpolatory \(\sqrt 3 \) subdivision, Computer Graphics Forum, 2000, 19: 131–138.

    Article  Google Scholar 

  18. Li G, Ma W, and Bao H, Interpolatory \(\sqrt 2 \)-subdivision surfaces, Proc. Geometric Modeling and Processing, 2004, 185–194.

  19. Beccari C, Casciola G, and Romani L, A unified framework for interpolating and approximating univariate subdivision, Applied Mathematics and Computation, 2010, 216: 1169–1180.

    Article  MathSciNet  Google Scholar 

  20. Luo Z and Qi W, On interpolatory subdivision from approximating subdivision scheme, Applied Mathematics and Computation, 2013, 220: 339–349.

    Article  MathSciNet  Google Scholar 

  21. Albrechta G and Romani L, Convexity preserving interpolatory subdivision with conic precision, Applied Mathematics and Computation, 2012, 219(8): 4049–4066.

    Article  MathSciNet  Google Scholar 

  22. Luo Z and Qi W, On interpolatory subdivision from approximating subdivision scheme, Applied Mathematics and Computation, 2013, 220(1): 339–349.

    Article  MathSciNet  Google Scholar 

  23. Cirak F, Ortiz M, and Schröder P, Subdivision surfaces: A new paradigm for thin shell analysis, International Journal of Numerical Methods in Engineering, 2000, 47: 2039–2072.

    Article  Google Scholar 

  24. Burckhart D, Hamann B, and Umlauf G, Iso-geometric finite element analysis based on Catmull-Clark subdivision solids, Computer Graphics Forum, 2010, 29(5): 1575–1584.

    Article  Google Scholar 

  25. Dikici E, Snare S R, and Orderud F, Isoparametric finite element analysis for Doo-Sabin subdivision models, Proceedings of Graphics Interface, 2012, 19–26.

  26. Yuan X and Tang K, Rectified unstructured T-splines with dynamic weighted refinement for improvement in geometric consistency and approximation convergence, Computer Methods in Applied Mechanics and Engineering, 2017, 316: 373–399.

    Article  MathSciNet  Google Scholar 

  27. Riffnaller-Schiefer A, Augsdorfera U, and Fellner D, Isogeometric shell analysis with NURBS compatible subdivision surfaces, Applied Mathematics and Computation, 2016, 272(1): 139–147.

    Article  MathSciNet  Google Scholar 

  28. Wei X, Zhang Y, Hughes T J, et al., Truncated hierarchical Catmull-Clark subdivision with local refinement, Computer Methods in Applied Mechanics and Engineering, 2015, 291: 1–20.

    Article  MathSciNet  Google Scholar 

  29. Wei X, Zhang Y, Hughes T J R, et al., Extended truncated hierarchical Catmull-Clark subdivision, Computer Methods in Applied Mechanics and Engineering, 2016, 299: 316–336.

    Article  MathSciNet  Google Scholar 

  30. Kang H, Li X, Deng J, et al., Truncated hierarchical Loop subdivision surfaces and application in isogeometric analysis, Computers and Mathematics with Applications, 2016, 72: 2041–2055.

    Article  MathSciNet  Google Scholar 

  31. Cashman T J, Augsdörfer U H, Dodgson N A, et al., NURBS with extraordinary points: High-degree, non-uniform, rational subdivision schemes, ACM Transactions on Graphics, 2009, 28(3): 1–9.

    Article  Google Scholar 

  32. Sederberg T, Zheng J, Sewell D, et al., Non-uniform Recursive Subdivision Surfaces, SIG-GRAPH’98, 1998, 387–394.

  33. Huang Z and Wang G, Non-uniform recursive Doo-Sabin surfaces, Computer-Aided Design, 2013, 43: 1527–1533.

    Article  Google Scholar 

  34. Muller K, Funfzig C, Reusche L, et al., DINUS-double insertion, non-uniform, stationary subdivision surfaces, ACM Transactions on Graphics, 2010, 29: 1–21.

    Article  Google Scholar 

  35. Li X, Finnigin T, and Sederberg T W, G1 non-uniform Catmull-Clark surfaces, ACM Transactions on Graphics, 2016, 35: 1–8.

    Google Scholar 

  36. Li X and Chang Y, Non-uniform interpolatory subdivision surface, Applied Mathematics and Computation, 2018, 274: 239–253.

    Article  MathSciNet  Google Scholar 

  37. Qin K and Wang H, Eigenanalysis and continuity of non-uniform doo-sabin surfaces, Proceedings of the 7th Pacific Conference on Computer Graphics and Applications, 1999, 179–186.

  38. Peters J and Reif U, Subdivision Surfaces, Springer, 2008.

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, China

    Md Nur Alam & Xin Li

Authors
  1. Md Nur Alam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xin Li.

Additional information

This research was supported by the National Natural Science Foundation of China under Grant No. 61872328, SRF for ROCS SE, and the Youth Innovation Promotion Association CAS, CAS-TWAS president’s fellowship program.

This paper was recommended for publication by Editor-in-Chief GAO Xiao-Shan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Alam, M.N., Li, X. Non-Uniform Doo-Sabin Subdivision Surface via Eigen Polygon. J Syst Sci Complex 34, 3–20 (2021). https://doi.org/10.1007/s11424-020-9264-z

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-020-9264-z

Keywords

Search

Navigation