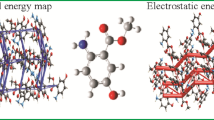
Abstract
The structures of selected thiobenzamides and some corresponding benzamides with two more or less bulky N-substituents have been studied by single-crystal X-ray diffraction analyses. The planarity of the thioamide moiety, i.e., the internal rotation about the Ar-CS and the C-N bond as well as the bending of the two N-substituents versus the thioamide plane, was determined from the data. The experimental data were corroborated by quantum chemical calculations of molecular ensembles in the crystal and, in particular, by Hirshfeld surface analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Although known since the nineteenth century, thioamides are still in the focus of chemists’ interest. They are important in drug design and peptide synthesis [1,2,3].
Due to the partial double bond character of the CN bond (Scheme 1), thioamides exhibit a more or less planar structure of the central skeleton.
However, deviations from planarity can occur on account of steric hindrance. Two different modes of disturbance demonstrated in Scheme 2 are possible: either rotation about the central CN bond by an angle Θ or bending of the N substituents by an angle δ between the SCR3 and the NR1R2 planes, i.e., deviation from sp2 hybridization at the nitrogen center.
It is well known since decades that the barriers for a 180° rotation about the C = N bond in thioamides are higher compared with the barriers in the corresponding amides [4,5,6,7,8] and are even high enough as to allow the separation of E/Z-stereoisomers with R2 ≠ R3 which are stable at room temperature [4, 9, 10]. This effect is obviously due to the lesser tendency of sulfur to form C = S double bonds compared with C = O bonds. Consequently, the sp2 configuration at the N center is more pronounced in thioamides and the planarity should be more distinct than in the corresponding amides.
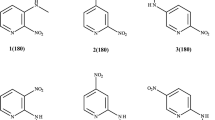
Ohwada et al. published a comprehensive study on the tunable planarity of thioamides [11]. They found out by X-ray structure analyses that the bicyclic N-thiobenzoyl-7-azabicyclo[2.2.1]heptane 1 significantly deviates from planarity in contrast to the related monocyclic pyrrolidino-thiobenzamide 2 and, expectedly, the deviation is more pronounced for the corresponding benzamides 1a and 2a [12].

We have prepared and studied a series of thiobenzamides and benzamides with two more or less bulky N-substituents as well as N,N,2,4,6-pentamethyl-thiobenzamide 15 the ortho-methyl groups of which should also cause considerable steric hindrance. Herein, we describe their NMR spectra, X-ray structures, and quantum-chemical calculations with a view on the pyramidalization at the nitrogen and on the torsion of the benzene ring versus the thioamide or amide plane. Furthermore, we take a view on the orientation of the molecules in the crystal by Hirshfeld surface analysis and calculation of the dispersion energies in the unit cell.
Experimental
Materials
N-tert-Butyl-N-methylamine, N-tert-butylaniline, di-tert-butylamine, 4-tert-butylbenzoyl chloride, and Lawesson’s reagent (LR) are commercially available. The thioamides were prepared either by thionation of the corresponding amides with P4S10 [13] or LR [14, 15] or by the one-pot procedure [16] from the corresponding acid chlorides, amines, and P4S10. For the details of the syntheses and the physical and spectroscopic data of all compounds confer the Supplemental Material file SM1.
X-Ray crystal structure determination
Agilent SuperNova Dual Source Diffractometer CuKα. Bruker SMART APEX CCD area-detector Diffractometer MoKα. CCDC: 3 (1,836,072), 3a, (2,018,834), 4 (1,836,073), 4a, (2,018,835), 6 (2,124,889), 7 (1,837,552), 8 (1,837,555), 9 (1,837,558), 10 (1,836,071), 10a (1,996,820), 11 (2,018,396), 11a (1,976,211), 12 (1,837,653), 13 (1,836,070), 14 (1,836,069), 14a (2,119,765), 15 (2,018,377).
Ortep plots of selected compounds are shown and discussed in the Results and Discussion section. Ortep plots of all compounds as well as the corresponding Tabs. with crystallographic data, details of data collection, and structure refinement parameters are given in the Supplemental Material files SM2 and SM3.
Computational aspects
All DFT and coupled cluster calculations including 1H and 13C NMR spectra were performed with the Orca program package (Version 5.0.2) [17], whereas computational crystal structure analysis was done by employing the Crystal Explorer 17.5 program [18].
The bond lengths, bond angles, and torsion angles of single molecules (“in the gas phase”) were calculated by applying Grimme’s composite B97-3c functional (Orca program) [19]. Interaction energies of the building blocks in the unit cell were obtained by applying the HFLD coupled-cluster approach [20] by the use of the local energy decomposition scheme (LED) [21,22,23,24,25]. Note: Gas phase static calculations refer to T = 0 K. All calculations of unit cells were performed by use of the CP2K-program, Version 8.1 (PBE functional; DZVP-GTH basis set, planewave cutoff 500 Ry) [26,27,28].
The calculations were executed on an AMD Ryzen Threadripper workstation or on the high-performance cluster at the data center (RRZ) of the University of Hamburg.
Results and discussion
The structures of a large number of thioamides have been determined by X-ray diffraction analyses. A survey at the CCDC provided as many as 89 hits for N,N-disubstituted arenecarbothioamides with 28 hits thereof for N-alkyl-N-aryl derivatives. However, neither N,N-diaryl- nor N-tert-alkyl-N-arylthiobenzamides are found in the data bank. Also, only four N-monosubstituted thioamides with N-tert-alkyl substituents have been studied.
For a more extensive study, we prepared several thiobenzamides of this type and performed single-crystal X-ray structure determinations (cf. Table 1). Unfortunately, our attempts to prepare N,N-di-tert-butylbenzamide (18a) were unsuccessful. Its synthesis is not described in the literature. Only MO calculations on its geometry and on its electronic distribution have been reported [29]. Acylation of di-tert-butylamine with benzoyl chloride led to N-tert-butylbenzamide under de-tert-butylation. Thus, the corresponding, and doubtlessly very interesting N,N-di-tert-butyl-thiobenzamide (18) could not be obtained. We also include thiobenzamides from earlier sources, the X-ray analyses of which have been performed but have not yet been published or have not been deposed at the CCDC. All thioamides considered in the present study are compiled in Table 1. X-ray structure analyses of selected related benzamides are also included for comparison.
E/Z-Stereoisomerism in solution as studied by NMR spectroscopy
As a consequence of the partial CN double bond character of thioamides [4, 5, 7, 8, 11, 38], two identical nitrogen substituents exhibit different chemical shifts of the 1H and 13C NMR signals. Accordingly, two diastereoisomers with E and Z configuration are frequently detected if the two substituents are different. Characteristic 1H and 13C NMR data compiled in Table 2 demonstrate these effects for selected thiobenzamides. NMR data of all thioamides studied are given in the Supplemental Material (SM1). We assigned the signals according to or in analogy with the literature [38,39,40,41,42] and considering the configurations observed in the crystalline state (see discussion of X-ray structural results, below).
The 1H and 13C NMR spectroscopic chemical shifts as calculated by use of the Orca program [17] in most cases agree well with the experimental results (see Table 2). Significant deviations are observed for the N,N-di-iso-propyl (7) and the N,N-di-cyclo-hexyl (9) derivatives. This is probably due to the complicated conformation within these N-substituents [38]. Also, the correct assignment of the signals to the respective E- or Z-configurations is corroborated by the calculations except for the two N,N-dimethyl derivatives 15 (13C) and 16 (1H and 13C) where the differences between the shifts of the two observed 13C signals are anyway very tiny.
At low temperature, the expected two 1H and 13C NMR signals are observed for the nuclei next to the nitrogen center of the symmetrically substituted thioamides 6, 7, 9, 15, and 16. Even the 1H and 13C signals of the CH3 groups in the β-position of N,N-di-iso-propyl-thiobenzamide 7 exhibit different chemical shifts at 223 K. This effect has been comprehensively studied by Berg and Pettersson [38] who also discussed the complicated gear effect caused by the different conformation of the four crowded methyl groups of 7. Coalescence of the signals due to free rotation about the N-CHMe2 bond and the partial CN double bond occur at elevated temperature.
The two diastereoisomers of 3 are clearly to distinguish at 223 K. An isomeric ratio E/Z = 3:2 follows from the intensity ratio of the methyl proton signals. The corresponding ratio for the trimethylsilyl derivative 5 is 9:1 at 243 K [42]. Only one 1H and one 13C signal for the central carbon atom of the N-tert-butyl substituent of 10 are observed at 223 K, 298 K and 378 K. Thus, N-tert-butyl-thiobenzanilide 10 obviously exists as a single diastereoisomer in solution with the sulfur neighboring the tert-butyl group (E-configuration according to the IUPAC rules!). The same result is observed for its 3,5-di-tert-butyl derivative 11.
E/Z-Stereoisomerism in the crystal as studied by X-ray structure analyses
According to X-ray analyses, N,N-dimethyl-thiobenzamides and -benzamides do not exhibit significant bending of the N substituents (Scheme 2). However, in spite of the partial C = N double bond character of amides and thioamides, torsion angles Θ2 > 0° (Scheme 3) are observed for the thiobenzamide 16 [11, 34, 36] and, more pronounced, for the corresponding benzamide 16a [33], even if these exhibit two least sterically demanding N-methyl substituents. N,N-Dimethyl-2,4,6-trimethyl-thiobenzamide 15 and, expectedly, N-methylthiobenzamide 17 with only one N-substituent neighboring the sulfur atom (Z configuration [37]) do not show significant torsion around the CN bond (Θ2 ≈ 0°, Scheme 3 and cf. also Table 3).
The angle Θ1 characterizing the torsion around the arene (thio-) amide bond of N,N-dimethyl derivatives (Scheme 3 and Table 3), on the other hand, is always far from 0°. Due to steric hindrance by the ortho-methyl groups, the arene ring of 15 is completely turned off the thioamide plane (Θ1 appr. 90°).
In our view, the angles Θ1 and Θ2 are the most obvious parameters for deviations from planarity within the molecules investigated.
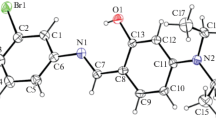
To find out if thiobenzamides with open-chained N-substituents considerably larger than methyl groups might show bending of the N-substituents, we determined the X-ray structures of selected thiobenzamides and, for comparison, of several related benzamides. Characteristic bond lengths d and bond angles \(\measuredangle\) of the studied compounds are compiled in Table 3. The amide 4a and the thioamides 3, 10 and 15 exhibit two and the thioamides 4 and 11 exhibit three independent molecules in the cell. Since the corresponding bond lengths d and bond angles \(\measuredangle\) do not significantly differ from each other, mean values of these data are given in the Tabs. For all individual data, see the Supporting Material (SM) or the Cifs deposed in the CCDC data bank. Ortep plots of each one molecule of the amides 3a, 4a, 10a, 11a, and 14a and of the thioamides 3–15 are shown in Figs. 3, 4, 5, and 6 and SM1-SM8.
The experimental bond lengths and angles are in accordance with data for other thioamides (see e.g., lit. [11, 37, 49,50,51,52]). Remarkably, no significant peculiarities are observed for thioamides with bulky N-substituents. Furthermore, the calculated data referring to single “gas phase” molecules agree well with the experimental results. The medians of the differences between experimental and calculated bond lengths (%) are Δd(C-X) = − 0.2, Δd(C-CAr) = − 0.8, Δd(C-N) = 1.2; and the medians of the bond angles (%) are \(\Delta \measuredangle\)(CCX) = 0.3, \(\Delta \measuredangle\)(CCN) = − 0.3, \(\Delta \measuredangle\)(XCN) = − 0.1 (reference compounds: 3–17), except for the thioamide 3 which exhibits a significantly increased C1-C7-N bond angle of 121.5° and a decreased C1-C7-S bond angle of 115.0° (see Table 3). This may be due to the unusual Z-configuration of 3 which causes enhanced steric hindrance between the sulfur atom and the tert-butyl group with widening and narrowing of the corresponding angles. All calculated C = S distances agree, however, well with the X-ray data. This is not a trivial result since C = S bond lengths obtained by quantum chemical calculations without consideration of dispersion forces significantly deviate from X-ray data [53].
The bond lengths calculated for the unit cell (CP2K; Functional PBE, DZVP-GTH basis set) are found systematically too long by ca. 1–4 pm (see Table 3). This effect is known from the lit. [46, 47]. E.g., for the CH3 group d(CH) = 107.9 pm (exp.) vs. 108.6 pm (calcd. with PBE). The deviation may be due to the application of less suitable parameters. The calculated bond angles in the unit cell (see Table 3), on the other hand, agree much better with the X-ray data.
The calculated Θ2 values (CP2K) for the unit cells of 16, 2, 3a, 6, and 6a significantly deviate from the X-ray values, which might be due to packing effects in the cell. Even employing the PBEsol-parametrization of PBE [54] which was designed for the calculation of solids and surfaces does not change torsions significantly, e.g., Θ1 = 60.3° and Θ2 = 7.3° for 3a.
The deviation from planarity of the benzamides and thiobenzamides can be derived from several experimental parameters.
The most easy to determine the sum Σ \(\measuredangle\)(R3CX) + \(\measuredangle\)(R3CN) + \(\measuredangle\)(XCN) of the three bond angles at the carbonyl/thiocarbonyl carbon of thiobenzamides and benzamides, expectedly, is 360.0 ± 0.1° which is indicative of the complete planarity at this center. N,N-Di-tert-butylbenzamide 18a with Σ \(\measuredangle (\mathrm{calcd}.)\) = 360.4° is somewhat off the range. In many cases, the sum N = α + β + γ (see Scheme 4) of the three bond angles at the nitrogen center is also 360°, i.e., ΔN = 0° within the experimental error. However, complete planarity at the nitrogen center of amides and thioamides is not self-evident! Despite the partial double bond character of the C = N bond and in contrast to the situation at the C = X center, one could well think of a deviation from planarity at the N center. A deviation may result from the above-mentioned bending of the N substituents of an angle δ between the R1-R2-N plane versus the X-C-R3 plane, i.e., a deviation from sp2 hybridization at the nitrogen may exist. In fact, significant pyramidalization for thiobenzamide 1 (ΔN = 2.5°) exhibiting a bicyclic N-substituent [11] and even more pronounced for the corresponding benzamide 1a (ΔN = 10.5°) [12] is observed, in contrast to the monocyclic pyrrolidides 2 and 2a. Ohwada defined the twist angle τ′ about the NCO bond as absolute mean value between the two torsion angles τ1 (R3CNR2) and τ2 (XCNR1), i.e., τ′abs = (τ1 + τ2)/2 as demonstrated in Scheme 4 [12] (see also Schemes 2 and 3).
Insignificant deviations ΔN (< 0.1 deg) of the sums Σ \(\measuredangle\)(R1NC) + \(\measuredangle\)(R2NC) + \(\measuredangle\)(R1NR2) from 360° are observed for many thiobenzamides and even for the respective benzamides. Table 4 shows the compounds with distances ω > 1 pm between the nitrogen and the plane opened by its three substituents CX, R1, and R2 together with ΔN, the simplest and clearest measure of the pyramidalization. The thiobenzamides 3, 6, 7, 8, 9, 10, and 14 with ωexp < 1 pm and ∆Nexp < 0.1 deg are neglected.
Figure 1 demonstrates the expected correlation (R = 0.9716) between ω and ∆N and the increasing pyramidal structure of the N-atom from the nearly planar thiobenzamide 17 to the most distinct pyramidalization of the benzamide 10a.
Correlation of distance ωexp and ∆N (see Table 4)
The torsion angles Θ1 between the arene (C1-C2-C6) and the amide/thioamide (X-C7-N) planes and Θ2 between the planes C1-C7-X and R1-N-R2 are compiled in Table 3. They characterize the out-of-plane geometry caused by Ar-CX and C-N bond rotation. Mean values are given in Table 3 in cases with two or three independent molecules in the unit cell. The thioamides 10 and 11 represent exceptions: the torsion angles of the independent molecules in their unit cells significantly deviate from each other (see the footnote of Table 3). Because of the above-mentioned possible pyramidalization at the N center, i.e., bending of the R1-N-R2 plane versus the C1-C7-X plane, the two torsion angles Θ1 (C1-CS-N-R2) and Θ2 (S-CS-N-R1) (see Scheme 4) may differ from each other. Thus, mean values Θ2 (footnote [b] and Table 3) are given for 10 and 11 in Table 3 [11, 12, 27].
Expectedly, the torsion angles Θ1 of thioamides and amides with N substituents larger than methyl groups in most cases are increased by ca. 10° and ca. 15°, respectively, compared with the values of ca. 60° for N,N-dimethylthiobenzamide 16 and ca. 50° for N,N-dimethylbenzamide 16a.
According to our calculations, the highly overcrowded N,N-di-tert-butyl-thiobenzamide 18 should represent an exceptional case (see Table 3) with an extremely high distortion of the partial CN double bond (Θ2 = 71.5°!) and a very low torsion of the benzene ring (Θ1 = 28.8°), which is demonstrated in Fig. 2. The remarkable distortion of the thioamide plane of 18 also corresponds with the calculated distance ω = 22 pm of the N atom from the plane of the three N substituents (see Table 3).
The variation of the experimental torsion angles Θ1 for the studied thiobenzamides and benzamides is summarized in Fig. 3. The values of the reference compounds 16 and 16a are marked with red circles.
Only each one diastereoisomer of the unsymmetrically substituted thiobenzamides 3, 4, 5, 10, and 11 and the benzamides 3a, 4a, and 10a exists in the crystal—also in cases with two or three independent molecules in the elemental cell. Thus, the question arises, which substituent adopts the syn-position neighboring the hetero atom, and which adopts the anti-position neighboring the benzene ring. Interestingly, the bulky tert-butyl groups of the thioamides 4, 10, and 11 and of the amides 3a, 4a, and 10a are oriented towards the sulfur or oxygen atoms (see Figs. 4, 5, 6, and 7) whereas the thioamide 3 (Fig. 4) and the N-trimethylsilyl derivative 5 (Fig. SM2) [30, 42] exist as the E-isomers with methyl groups neighboring the sulfur atom. In their recent publication, Song et al. [52] furthermore described the influence of solvents on the Z/E preference of N-aryl-thioacetamides and corroborated their results with DFT calculations.
Analysis of interactions in the unit cell
Since we had calculated significant changes of the geometric parameters of the considered amides and thioamides in the crystal, compared with the single molecule, which we had assigned to steric crowding, we further analyzed the interaction energies in the unit cell. We used the analysis of Hirshfeld surfaces [55,56,57,58] which has been established during the last decade and has proved to be a most suitable tool of investigation. In particular, the analysis of the so-called fingerprint regions allows visualization of close contacts between molecules in an ensemble like a unit cell (Supporting information Table SM4ff).
Following the basic ideas of Spackman, various functions can be mapped on Hirshfeld surfaces [55]. The distances de of the surface from the nearest nucleus outside and di of the surface from the nearest nucleus inside, respectively, are the important functions. The mapping of de and di pairs as a function of the fraction of surface points in a discrete section generates so-called fingerprint plots (color scheme: blue few points—green—red many points). These plots are unique for the given molecule and highly sensitive to the environment of the molecule shown for thiobenzamide 3 in Fig. 8 as an example (for other cases, cf. the Figs. in the SM).
Thiobenzamide 3 (B3LYP 6-31G**). a Visualization of Hirshfeld-surface; dotted lines represent H-bonding/H–H close contacts between molecules. Isosurface 0.5 /function dnorm. b Fingerprint plot of the Hirshfeld surface. Marked spikes represent H–H-close contacts. Figure 8 was generated by Crystal Explorer V 17.5 [18]
The combination of the de and di values, normalized by the van der Waals radius, is called contact distance dnorm. The dnorm surface is extremely useful to quantify close contacts as a histogram [55, 57] which shows the contribution of the various intermolecular close contacts in a given ensemble of molecules, e.g., a unit cell.
Hence, we calculated the close contact distribution of the studied set of amides and thioamides. As demonstrated in Fig. 9, increasing C-close contacts cause decreasing H-close contacts. The C–C-close contacts represent π-π-interaction. Aromatic substituents obviously force this effect. This is in accordance with the observed ranking. The N-close contacts (appr. 0.1%) do not play a vital role (see Fig. 9 and Supporting Information Tabs. SM4ff).
Calculation and discussion of energies, aromaticity, and interaction
Finally, we calculated the interaction energies of the molecules in the unit cells by use of the HFLD method (Hartree–Fock plus London Dispersion) [20], an adaptation of the domain-based local pair natural orbital coupled cluster-framework (DLPNO-CCSD(T)) developed by Neese and coworkers [17, 21,22,23,24,25]. This approach allows local energy decomposition (LED) of the interaction energies of fragments as they can be defined in unit cells of crystal structures. The LED LD contribution calculated by this method is quite similar to that obtained from a full DLPNO-CCSDT(T) calculation at lower computational cost [20].
Interaction energies and Hirshfeld surface analyses of all benzamides and thiobenzamides compiled in Table 1 are considered in Fig. 9 and Table 5. Unit cells have been generated by packing the corresponding CIF files using the MERCURY program [59]. Thus, moieties of up to the 516 atoms in the case of thiobenzamide 4 were generated. To make computations feasible within an appropriate time frame, we extracted dimers. In principle, compounds may be calculated up to 248 atoms in eight fragments as in 3 (this study) but, as well as, e.g., in cyclohexanone monooxygenase [20]. Limiting factors are the memory (RAM) and disk space of the used scratch directories.
All dimers were calculated by use of an augmented correlation consistent basis set including polarization functions as well as an auxiliary basis set to take the RIJK approach [60, 61] into account (aug-cc-pVDZ aug-cc-pVDZ/C aug-cc-pVTZ/JK [62,63,64,65]). The RIJK approach is crucial to assure single pair energy contribution less than 10‒6 a.u. as a diagnostic for tightly converged SCF. To save wall clock time, we decided to use the NormalPNO and TightSCF-setting accepting a slight loss of accuracy.
Furthermore, we determined the π-interaction using the local orbital locator (LOL) approach [66] and the harmonic oscillator measure of aromaticity (HOMA) indices [67]. The basis of the LOL as delocalized exchange, which depends on the non-interacting kinetic energy density, has been described by Schmider and Becke [68]. The HOMA model in its revised form intends to measure inter- and intramolecular interactions in the crystalline state [67]. It relies on the idea that σ-bonds tend to form bonds of equal length whereas π-bonds tend to form bonds of alternating lengths (localized bonds). The bonds of the real molecule are expected to have bond lengths in between. The author stated that aromaticity by the revised HOMA index in aromatic rings of various compounds depends rather weakly on the planarity of the system whereas it seems to be strongly dependent on intermolecular H-bonding as well as on substituent interactions.
HOMA indices are between 1 (fully aromatic) and 0 (completely nonaromatic) [67]. The HOMA analysis is still of interest for tailoring special characteristics of organic compounds [69].
The LOLIPOP index is defined as definite integral of the localized orbital locator of π-orbitals (LOL-π) within a cylindric range perpendicular to the plane of the ring considered (ref. to SM 5). Low LOLIPOP values indicate higher delocalization (π-depletion), lower aromaticity, and more pronounced π-interaction ability. Calculation of the LOL indices (LOL integrated π-over planes: LOLIPOP), which provides an indication of the π-π-interaction in aromatic systems, and of the HOMA indices, were performed with MULTIWFN V.3.8 [70, 71]. It is crucial to use the Molden input format based on the binary wavefunction file from the ORCA output (HFLD-runs; localized orbitals). For all calculations, default values were used.
The investigation of π-π-interactions, often called π-stacking, must be discussed with care! Grimme [72, 73] and Iverson [74] pointed out that this kind of interaction becomes more and more relevant in dimers with more than approximately 15 carbon atoms. Its driving force results from the geometry of the dimers including substituent effects. The dispersion component and the correlation effects between π-electrons of interacting dimers are the dominating factors of this type of interaction. The dispersion effect is strengthened if the π-planes of the monomers become more and more parallel emerging a stacked conformation.
To shed light on the details of interaction between the dimers considered, we clustered the amides and thioamides into four groups—A, B, C, and D—depending on the substituents at the N-atom.
-
Cluster A: 1 and 2: N-atom is part of a ring system.
-
Cluster B: 3, 3a, 4, 4a, 7, 8, 9, 15, 16, 16a, 17: both N substituents R1 and R2 are aliphatic.
-
Cluster C: 10, 10a, 11, 11a: R1 is aromatic, R2 is aliphatic (or vice versa).
-
Cluster D: 6, 6a, 12, 12a, 13, 14, 14a: both N substituents R1 and R2 are aromatic.
The different clusters can be depicted as follows (see Table 5 and LOLIPOP reference benzene with LOLIPOP-index 7.28 [66]).
Only the thiobenzamides 1, 2, 4, 11, 12, 15, 16, and 17 and the benzamides 3a, 4a, 6a, 10a, 11a, 12a, 14a, and 16a show significant deviations ω from a planar structure of the C-NR1-NR2-group (see Table 4 and Fig. 1). N-tert-Butylbenzanilide 10a exhibits the highest degree of non-planarity of all compounds considered. The resulting median values for ω are as follows: Cluster D 7.0 < cluster B 8.2 < cluster A 8.6 < cluster C 9.7. Thus, the N-aliphatic–aromatic substituted amides and thioamides bearing bulky substituents (cluster C) exhibit the most distinct quasi-pyramidal structure at the N-atom.
The HOMA and LOLIPOP indices for the Clusters B–D reveal the opposite order of the median values, i.e., HOMA median: Cluster D < cluster B < cluster C < cluster A; LOLIPOP median: Cluster C < cluster B < cluster A < cluster D. This result is in accordance with the idea that higher aromaticity causes less delocalization and, consequently, lower LOLIPOP values. Due to specific steric demand, cluster A represents an exceptional case.
According to the energy calculations, aromatic substituents at the N-atom and bulky substituents at the rings cause increasing dispersion energies. The absolutely highest dispersion energy (‒22 kcal mol‒1) is observed for the highly crowded N,N-diphenyl-3,5-di-tert-butyl-thiobenzamide 14. The lowest dispersion energy (‒1.5 kcal mol‒1) is found for N,N-dimethyl-thiobenzamide 17. Thiobenzamide 14 and the corresponding benzamide 14a exhibit the utmost difference of dispersion energies (‒13.3 kcal mol‒1). Comparison of the other pairs of thioamides/amides reveals differences of dispersion energies between ‒3.9 kcal mol‒1 and + 3.9 kcal mol‒1. The benzamides 3a, 4a, 10a, 11a, and 16 exhibit higher dispersion and correlation energies than the corresponding thiobenzamides (Fig. 10).
Conclusions
Our experimental and theoretical results reveal that the N-planarity of thiobenzamides is less pronounced as compared with the corresponding benzamides.
Twenty-four amides and thioamides have been investigated by X-ray diffraction analysis as well as by quantum chemical methods. Calculated geometries—in the gas phase and in unit cells—are in good accordance with experimental results. Over all compounds, the carbonyl and thiocarbonyl moiety can be considered as completely planar at the CS/CO centers. However, sixteen of the investigated compounds exhibit, to some extent, significant deviation from the planar structure at the C-NR1-NR2-moiety. The Hirshfeld surfaces were calculated to identify intermolecular close contacts. N,N-Dialkyl-thiobenzamides and -benzamides exhibit the closest H–H contacts and the weakest C–C contacts whereas the N,N-diaryl-thiobenzamides and -benzamides show the opposite effect. These results, furthermore, indicate that expectedly the bulky alkyl substituents in 4, 4a, 8, and 9 force H–H close contacts in the unit cells.
Dispersion and correlation energies were calculated by the HFLD-method. As expected, crowding leads to high dispersion and correlation energies as can be observed for 1, 4a, 11, 11a, 12, 12a, 13, and 14.
Data availability
X-ray data are available at the CCDC.
References
Mahanta N, Szantai-Kis DM, Petersson EJ, Mitchell DA (2019) Biosynthesis and chemical applications of thioamides. ACS Chem Biol 14:142–163. https://doi.org/10.1021/acschembio.8b01022
Camacho LA III, Lampkin BJ, VanVeller B (2019) A bottom-up approach to preserve thioamide residue stereochemistry during Fmoc solid-phase peptide synthesis. Org Lett 21:7015–7018. https://doi.org/10.1021/acs.orglett.9b02598
Mach P, Budzák Š, Juhász G (2014) Theoretical study (CC2, DFT and PCM) of charge transfer complexes between antithyroid thioamides and TCNE. J Mol Model 20:2312(1–16). https://doi.org/10.1007/s00894-014-2312-7
Walter W, Maerten G (1963) Thioformylierung von Aminen und Untersuchungen über die cis-trans-Isomerie an der ThioamidgruppeLiebigs Ann Chem 669:66–75
Stewart WE, Siddall TH III (1970) Nuclear magnetic resonance studies of amides. Chem Rev 70:517–551
Sandström J (1967) Barriers to internal rotation in thioamides. Experimental results and molecular orbital calculations. J Phys Chem 71:2318–2325. https://doi.org/10.1021/j100866a055
Walter W, Schaumann E, Voss J (1971) The difference in the barrier heights for internal rotation between amides and thioamides. Org Magnet Reson 3:733–735. https://doi.org/10.1002/mrc.127003061
Wiberg K, Rablen PR (1995) Why does thioformamide have a larger rotational barrier than formamide? J Am Chem Soc 117:2201–2209. https://doi.org/10.1021/ja00113a009
Walter W, Schaumann E, Reubke K-J (1968) Separation and properties of the cis-trans-Isomers of N-Alkylthioformamides. Angew Chem Int Ed 7:467. https://doi.org/10.1002/anie.196804671
Walter W, Schaumann E (1971) Über die Struktur der Thioamide und ihrer Derivate, XV. Trennung der geometrischen Isomeren und Bestimmung der Rotationsbarrieren bei N-Alkyl-thioamiden. Chem Ber 104:3361–3377. https://doi.org/10.1002/cber.19711041103
Hori T, Otani Y, Kawahata M, Yamaguchi K, Ohwada T (2008) Nonplanar structures of thioamides derived from 7-Azabicyclo[2.2.1]-heptane. Electronically Tunable Planarity of Thioamides. J Org Chem 73:9102–9108. https://doi.org/10.1021/jo8011996b
Otani Y, Nagae O, Naruse Y, Inagaki S, Ohno M, Yamaguchi K, Yamamoto G, Uchiyama M, Ohwada T (2003) An evaluation of amide group planarity in 7-Azabicyclo[2.2.1]heptane Amides. Low amide bond rotation barrier in solution. J Am Chem Soc 125:15191–15199. https://doi.org/10.1021/ja036644z
Voss J, Walter W (1970) EPR-Untersuchungen an Thioamiden, II. N, N-Dialkyl-thiobenzamid-Radikal-Anionen Liebigs. Ann Chem 734:1–12
Voss J (1995) 2,4-Bis(4-methoxyphenyl)-1,3,2,4-dithiadiphosphetane 2,4-Disulfide. In: Paquette LA, Burke SD (eds) Encyclopedia of Reagents for Organic Synthesis, 1st edn vol 1. John Wiley & Sons Ltd., Chichester, 530–534
Voss J (2006) 2,4-Bis(4-methoxyphenyl)-1,3,2,4-dithiadiphosphetane 2,4-Disulfide. In: Electronic Encyclopedia of Reagents for Organic Synthesis. Paquette LA, Crich D eds), 2nd edn vol 1, John Wiley & Sons Ltd., Chichester, 1-16. ISBN: 978-0-470-84289-8. http://www.mrw.interscience.wiley.com/eros/articles/rb170/sect0.html
Voss J, Walter W (1968) Direkte Darstellung von Thioamiden aus Säurechloriden und Aminen. Liebigs Ann Chem 716:209–211
Neese F (2022) The ORCA Program System. – Version 5.0. WIREs Wiley Interdiscip Rev: Comput Mol Sci 12:e1606. https://doi.org/10.1002/wcms.1606
Wolff SK, Grimwood DJ, McKinnon JJ, Turner MJ, Jayatilaka D, Spackman MA (2012) CrystalExplorer (Version 17.5), University of Western Australia.
Brandenburg JG, Bannwarth C, Hansen A, Grimme S (2018) B97–3c: A revised low-cost variant of the B97-D density functional method. J Chem Phys 148:064104-1–064104-13. https://doi.org/10.1063/1.5012601
Altun A, Neese F, Bistoni G (2019) HFLD: A nonempirical London Dispersion-Corrected Hartree−Fock method for the quantification and analysis of noncovalent interaction energies of large molecular systems. J Chem Theory Comput 15:5894–5907. https://doi.org/10.1021/acs.jctc.9b00425
Altun A, Neese F, Bistoni G (2018) Local energy decomposition analysis of hydrogen-bonded dimers within a domain-based pair natural orbital coupled cluster study. Beilstein J Org Chem 14:919–929. https://doi.org/10.3762/bjoc.14.79
Liakos DG, Neese F (2015) Is it possible to obtain coupled cluster quality energies at near density functional theory cost? Domain-based local pair natural orbital coupled cluster vs modern density functional theory. J Chem Theory Comput 11:4054–4063. https://doi.org/10.1021/acs.jctc.5b00359
Altun A, Neese F, Bistoni G (2019) Effect of electron correlation on intermolecular interactions: a pair natural orbitals coupled cluster based local energy decomposition study. J Chem Theory Comput 15:215–228. https://doi.org/10.1021/acs.jctc.8b00915
Yepes D, Neese F, List B, Bistoni G (2020) Unveiling the delicate balance of steric and dispersion interactions in organocatalysis using high-level computational methods. J Am Chem Soc 142:3613–3625. https://doi.org/10.1021/jacs.9b13725
Lu Q, Neese F, Bistoni G (2019) London dispersion effects in the coordination and activation of alkanes in σ-complexes: a local energy decomposition study. Phys Chem Chem Phys 21:11569–11577. https://doi.org/10.1039/c9cp01309a
Del Ben M, Schütt O, Wentz T, Messmer P, Hutter J, VandeVondele J (2015) Enabling simulation at the fifth rung of DFT: Large scale RPA calculations with excellent time to solution. Comp Phys Commun 187:120–129. https://doi.org/10.1016/j.cpc.2014.10.021
Kuehne, TD, Iannuzzi M, Del Ben M, Rybkin VV, Seewald P, Stein F, Laino T, Khaliullin RZ, Schuett O, Schiffmann F, Golze D, Wilhelm J, Chulkov S, Bani-Hashemian, MH Weber V, Borstnik U, Taillefumier M, Jakobovits AS, Lazzaro A, Pabst H, Mueller T, Schade R, Guidon M, Andermatt S, Holmberg N, Schenter GK, Hehn A, Bussy A, Belleamme F, Tabacchi G, Gloess A, Lass M, Bethune I, Mundy CJ, Plessl C, Watkins M, VandeVondele J, Krack M, Hutter J (2020) CP2K: an electronic structure and molecular dynamics software package I. quickstep: efficient and accurate electronic structure calculations. ArXiv.org, e-Print Archive Phys 1–51
Hartwigsen C, Goedecker S, Hutter J (1998) Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys Rev B58:3641–3662. S0163–1829(98)05628–8
Mujika JI, Matxain JM, Ericsson LA, Lopez X (2006) Resonance structures of the amide bond: advantage of planarity. Chem Eur J 12:7215–7224. https://doi.org/10.1002/chem.200600052
Lüke H-W (1978) Silylthioamide Eigenschaften und Reaktionen, PhD thesis. Univ. Hamburg, Germany
Harto S (1976) Röntgenstrukturanalyse von Carbonyl- und Thiocarbonyl-Verbindungen mit sp2- und sp-hybridisiertem Kohlenstoff, PhD thesis. Univ. Hamburg, Germany
Choudhury D, Banik A, Sarma R (2010) N, N-Diphenylbenzamide Acta Crystallogr Crystal Struct Commun C 66:o524–o526. https://doi.org/10.1107/S0108270110036887
Karlsen H, Kolsaker P, Rømming C, Uggerud E (2002) The analogy between C=O and C(CN)2. Part 2. 1 Structural properties of N, N-Dialkylaminobenzamides and the analogously substituted 2-(Phenylmethylene)propanedinitriles J Chem Soc Perkin Trans 2:404–409. https://doi.org/10.1039/b105532c
Walter W, Harto S, Voss J (1976) N, N-Dimethylthiobenzamid Acta Crystallogr B 32 2876 2877. https://doi.org/10.1107/S0567740876009084
Harto S (1974) Röntgenographische Untersuchungen zur Molekülstruktur des N,N-Dimethylthiobenzamids Diploma thesis. Univ. Hamburg
Basu B, Kundu S (2014) Unprecedented amidation of ‘Transient’ Aryl Thioaldehydes by N, N-dimethylformamide under basic conditions New J Chem 38:3367–3370. https://doi.org/10.1039/c4nj00480a
Śmiszek-Lindert W, Nowak M, Kusz J (2007) N-Methylthiobenzamide. Acta Crystallogr E, Structure Repo Online 63:o4030. https://doi.org/10.1107/S1600536807043723
Berg U, Pettersson I (1985) Conformational equilibria and torsional barriers of the Isopropyl groups in N, N-Diisopropylbenzamide and its thio and seleno analogues. Magn Reson Chem 23:536–539. https://doi.org/10.1002/mrc.1260230711
Holík M, Mannschreck A (1979) Application of NMR spectroscopy of Chiral Association Complexes. 8. Rotation about the C(sp2)-C(aryl) Bond in 2,6-Disubstituted Benzamides. Org Magn Reson 12:223–228. https://doi.org/10.1002/mrc.1270120411
Walter W, Maerten G, Rose H (1966) NMR-spektroskopische Untersuchungen an cis- und trans-N-Methyl-N-benzylthioformamid. Zuordnung der Konfigurationen und Kinetik der Umwandlung. Liebigs Ann Chem 691:25–32
Rae ID (1979) Carbon-13 NMR spectra of some amides and lactams and their thio and seleno analogs. Austral J Chem 32:567–573. https://doi.org/10.1071/CH9790567
Walter W, Lüke H-W, Voss J (1975) Über die Struktur der Thioamide und ihrer Derivate. XXXVI - N-(Trimethylsilyl)thioamide I. Liebigs Ann Chem 1808–1821
Khatri CK, Mali AS, Chaturbhuj GU (2017) Sulfated polyborate catalyzed kindler reaction: a rapid, efficient, and green protocol. Monatsh Chem 148:1463–1468. https://doi.org/10.1007/s00706-017-1944-6
Yousif NM, Salama MA (1989) The reaction of carboxylic acid chlorides with 2,4-Bis(4-methoxyphenyl)-1,3,2,4-dithiadiphosphetane 2,4-Disulfide. Egypt J Chem 30:519–522
Mannschreck A, Mattheus A, Rissmann G (1967) Comparison of kinetic results obtained by NMR line shape and equilibration methods. J Mol Spectrosc 23:15–31. https://doi.org/10.1016/0022-2852(67)90044-6
Xu X, Goddard WA III (2004) The extended Perdew-Burke-Ernzerhof functional with improved accuracy for thermodynamic and electronic properties of molecular systems. J Chem Phys 121:4068–4082. https://doi.org/10.1063/1.1771632
Ernzerhof M, Scuseria GE (1999) Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J Chem Phys 110:5029–5036. https://doi.org/10.1063/1.478401
Achar TK, Mal P (2015) Radical-induced metal and solvent-free cross-coupling using TBAI−TBHP: oxidative amidation of aldehydes and alcohols with N-Chloramines via C−H activation. J Org Chem 80:666–672. https://doi.org/10.1021/jo502464n
Eccles KS, Morrison R, Maguire AR, Lawrence SE (2014) Crystal landscape of primary aromatic thioamides. Cryst Growth Des 14:2753–2762. https://doi.org/10.1021/cg401891f
Śmiszek-Lindert W, Chełmecka E, Dudzińska A (2016) Hirshfeld surface analysis and spectroscopic and DFT studies of p-Acetotoluidide and p-Thioacetotoluidide. Struct Chem 27:1093–1106. https://doi.org/10.1007/s11224-015-0731-4
Lai M, Wu Z, Wang Y, Zheng Y, Zhao M (2019) Selective synthesis of aryl thioamides and Aryl-α-ketoamides from α-Oxocarboxylic acids and tetraalkylthiuram disulfides: an unexpected chemoselectivity from arylsulfonyl chlorides. Org Chem Front 6:506–511. https://doi.org/10.1039/c8qo01127c
Song S, Hyodo T, Ikeda H, Vu KAL, Tang Y, Chan ES, Otani Y, Inagaki S, Yamaguchi K, Ohwada T (2022) Contribution of solvents to geometrical preference in the Z/E equilibrium of N-Phenylthioacetamide. J Org Chem 87:1641–1660. https://doi.org/10.1021/acs.joc.1c00801
Voss J, Buddensiek D, Adiwidjaja G (2019) Preparation and structure of 4-(Dimethylamino)thiopivalophenone – intermolecular interactions in the crystal. Z Naturforsch 74b:825–831 and refs. cited therein. https://doi.org/10.1515/znb-2019-0113
Perdew JP, Ruzsinszky A, Czonka GI, Vydrov OA, Scuseria GE, Constantin LA, Hou X, Burke K (2008) Restoring the density-gradient expansion for exchange in solids and surfaces. Phys Rev Lett 100:136406. https://doi.org/10.1103/PhysRevLett.100.136406. Erratum (2009) Phys Rev Lett 102:039902. https://doi.org/10.1103/PhysRevLett.102.039902
Spackman MA, Jayatilaka D (2009) Hirshfeld surface analysis Cryst Eng Commun 11:19–32. https://doi.org/10.1039/b818330a
Spackman MA, McKinnon JJ (2002) Fingerprinting intermolecular interactions in molecular crystals. Cryst Eng Commun 4:378–392. https://doi.org/10.1039/b203191b
McKinnon JJ, Jayatilaka D, Spackman MA (2007) Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces. Chem Commun 3814–3816. https://doi.org/10.1039/b704980c
Hirshfeld FL (1977) Bonded-atom fragments for describing molecular charge densities. Theoret Chim Acta 44:129–138. https://doi.org/10.1007/BF00549096
Macrae CF, Sovago I, Cottrell SJ, Galek PTA, McCabe P, Pidcock E, Platings M, Shields GP, Stevens JS, Towler M, Wood PA (2020) Mercury 4.0: from visualization to analysis, design and prediction. J Appl Cryst 53:226–235. https://doi.org/10.1107/S1600576719014092
Eichkorn K, Treutler O, Öhm H, Häser M, Ahlrichs R (1995) Auxiliary basis sets to approximate Coulomb potentials. Chem Phys Lett 240:283–290. https://doi.org/10.1016/0009-2614(95)00621-A. Erratum 242:652–660. https://doi.org/10.1016/0009-2614(95)00838-U
Weigend F, Häser M, Patzelt H, Ahlrichs R (1998) RI-MP2: optimized auxiliary basis sets and demonstration of efficiency. Chem Phys Lett 294:143–152. https://doi.org/10.1016/s0009-2614(98)00862-8
Kendall RA, Dunning TH Jr, Harrison RJ (1992) Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J Chem Phys 96:6796–6806. https://doi.org/10.1063/1.462569
Prascher BP, Woon DE, Peterson KA, Dunning TH Jr, Wilson AK (2011) Gaussian basis sets for use in correlated molecular calculations. VII. Valence, core-valence, and scalar relativistic basis sets for Li, Be, Na, and Mg. Theor Chem Acc 128:69–82. https://doi.org/10.1007/s00214-010-0764-0)
Woon DE, Dunning TH Jr (1993) Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J Chem Phys 98:1358–1371. https://doi.org/10.1063/1.464303
Weigend F, Köhn A, Hättig C (2002) Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J Chem Phys 116:3175–3183. https://doi.org/10.1063/1.1445115
Gonthier JF, Steinmann SN, Roch L, Ruggi A, Luisier N, Severin K, Corminbœuf C (2012) π-Depletion as a criterion to predict π-stacking ability. Chem Commun 48:9239–9241. https://doi.org/10.1039/c2cc33886f
Krygowski TM (2000) Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of π-electron systems. J Chem Inf Comput Sci 33:70–78. https://doi.org/10.1021/CI00011a011
Schmider HL, Becke AD (2000) Chemical content of the kinetic energy density. J Mol Struct (Theochem) 527:51–61. https://doi.org/10.1016/S0166-1280(00)00477-2
Gilani M, Saeidian H, Mirjafary Z (2020) Harnessing aromaticity and intramolecular hydrogen bonding to tailor organosuperbases by using 2,4,6-cycloheptatriene-1-imine scaffold. Struct Chem 31:1545–1551. https://doi.org/10.1007/s11224-020-01520-0
Lu T, Chen Q (2020) A simple method of identifying π orbitals for non-planar systems and a protocol of studying π electronic structure. Theor Chem Acc 139:25(12pp.). https://doi.org/10.1007/s00214-019-2541-z
Lu T, Chen F (2012) Multiwfn: a multifunctional wavefunction analyzer. J Comput Chem 33:580–592. https://doi.org/10.1002/jcc.22885
Grimme S (2008) Do special noncovalent π–π stacking interactions really exist? Angew Chem Int Ed 47:3430–3434. https://doi.org/10.1002/anie.200705157
Plett CS, Grimme S (2023) Automated and efficient generation of general molecular aggregate structures. Angew Chem Int Ed 62:e202214477. https://doi.org/10.1002/anie.202214477
Martinez CR, Iverson BL (2012) Rethinking the term “pi-stacking.” Chem Sci 3:2191–2201. https://doi.org/10.1039/C2SC20045G
Acknowledgements
Manfred Krasmann (preparations), Dr. Thomas Hackl (NMR spectroscopy), Thorsten Mix, MS (NMR spectroscopy), Prof. Dr. Ulrich Behrens, Dr. Frank Hoffmann and Isabelle Nevoigt (X-ray) are acknowledged for experimental assistance and competent expert advice. We also thank Prof. Frank Neese and Dr. Frank Wennmohs, Max Planck Institut für Kohlenforschung, for providing the ORCA 5.0.2 program and Dr. Thomas Orgis, RRZ, for advice and support concerning the RRZ hardware and software.
Funding
Open Access funding enabled and organized by Projekt DEAL. This study is financially supported by the University of Hamburg, Hamburg, Germany,
Author information
Authors and Affiliations
Contributions
The authors of the current manuscript Jürgen Voss and Dirk Buddensiek contributed equally to this work. They read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Voss, J., Buddensiek, D. Sterically crowded thioamides: deviations from planarity as determined by X-ray structure analyses and quantum chemical calculations. Struct Chem 34, 1623–1639 (2023). https://doi.org/10.1007/s11224-023-02189-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11224-023-02189-x