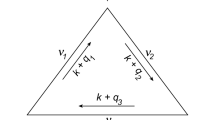
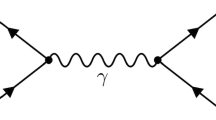
Abstract
Using Hilbert transforms, we establish two families of sum rules involving Bessel moments, which are integrals associated with Feynman diagrams in two-dimensional quantum field theory. With these linear relations among Bessel moments, we verify and generalize two conjectures by Bailey–Borwein–Broadhurst–Glasser and Broadhurst–Mellit.
Similar content being viewed by others
Notes
For our purposes, it suffices to evaluate the Hilbert transform of a function for almost every (a.e.) real variable, leaving out a subset of measure zero that will not affect subsequent computations of Lebesgue integrals. Later afterwards, an equal sign may also be used to denote an equality that is valid almost everywhere (even when “a.e.” is not written), depending on context.
Confusingly, in [1, footnote 13], the authors apparently declared that the conjecture on \( Z_{2n,n-2k}=0\) “has also now been resolved,” without supplying further citations to publications or preprints. This contradicts the recent claims in [5, (112)] and [9, (5.6)] on the open status of \( Z_{6,1}=0.\)
Naïvely, upon observing that \( (n!)^2/2^n\in \mathbb Z,\,{\forall } n\in \mathbb Z_{\ge 4}\) and \( D_n\in \mathbb Z,\,{\forall } n\in \mathbb Z_{\ge 0},\) we obtain \( 2^{\ell -1}\alpha _\ell \in \mathbb Z,\,{\forall } \ell \in \mathbb Z_{>0},\) at best. The divisibility statement \( 4^{n}\mid (n!)^2D_n,\,{\forall } n\in \mathbb Z_{\ge 0}\) is thus deeper than these naïve observations. In our proof of the integrality \( \alpha _\ell \in \mathbb Z,\,{\forall } \ell \in \mathbb Z_{>0},\) we need Rogers’ work on modular forms [15], which in turn, was inspired by Bertin’s studies of modular parametrizations for certain families of Calabi–Yau manifolds [2].
References
Bailey, D.H., Borwein, J.M., Broadhurst, D., Glasser, M.L.: Elliptic integral evaluations of Bessel moments and applications. J. Phys. A 41(20), 205203 (2008)
Bertin, M.J.: Mesure de Mahler d’hypersurfaces \(K3\). J. Number Theory 128(11), 2890–2913 (2008)
Bloch, S., Kerr, M., Vanhove, P.: A Feynman integral via higher normal functions. Compos. Math. 151(12), 2329–2375 (2015)
Borwein, J.M., Salvy, B.: A proof of a recurrence for Bessel moments. Exp. Math. 17(2), 223–230 (2008)
Broadhurst, D.: Feynman integrals, \({L}\)-series and Kloosterman moments. Commun. Number Theory Phys. 10(3), 527–569 (2016)
Broadhurst, D.: \({L}\)-series from Feynman diagrams with up to 22 loops. In: Workshop on Multi-loop Calculations: Methods and Applications, Paris, France, 7 June 2017. Séminaires Internationaux de Recherche de Sorbonne Universités. https://multi-loop-2017.sciencesconf.org/data/program/Broadhurst.pdf
Broadhurst, D.: Combinatorics of Feynman integrals. In: Combinatoire Algébrique, Résurgence, Moules et Applications, Marseille-Luminy, France, 28 June 2017. Centre International de Rencontres Mathématiques. http://library.cirm-math.fr/Record.htm?idlist=29&record=19282814124910000969
Broadhurst, D.: Feynman integrals, beyond polylogs, up to 22 loops. In: Amplitudes 2017, Edinburgh, Scotland, UK, 12 July 2017. Higgs Centre for Theoretical Physics. https://indico.ph.ed.ac.uk/event/26/contribution/21/material/slides/0.pdf
Broadhurst, D., Mellit, A.: Perturbative quantum field theory informs algebraic geometry. In: Loops and Legs in Quantum Field Theory. PoS (LL2016) 079, 2016
Groote, S., Körner, J.G., Privovarov, A.A.: On the evaluation of a certain class of Feynman diagrams in \(x\)-space: sunrise-type topologies at any loop order. Ann. Phys. 322, 2374–2445 (2007)
King, F.W.: Hilbert Transforms (Volume 1). Encyclopedia of Mathematics and Its Applications, vol. 124. Cambridge University Press, Cambridge (2009)
King, F.W.: Hilbert Transforms (Volume 2). Encyclopedia of Mathematics and Its Applications, vol. 125. Cambridge University Press, Cambridge (2009)
Ouvry, S.: Random Aharonov–Bohm vortices and some exactly solvable families of integrals. J. Stat. Mech. Theory Exp. 1, P09004 (2005)
Rogers, M., Wan, J.G., Zucker, I.J.: Moments of elliptic integrals and critical \({L}\)-values. Ramanujan J. 37(1), 113–130 (2015)
Rogers, M.D.: New \(_5F_4\) hypergeometric transformations, three-variable Mahler measures, and formulas for \(1/\pi \). Ramanujan J. 18(3), 327–340 (2009)
Samart, D.: Feynman integrals and critical modular \(L\)-values. Commun. Number Theory Phys. 10(1), 133–156 (2016)
Sloane, N.J.A.: Sequence A262961—Crandall numbers. In: The On-line Encyclopedia of Integer Sequences. https://oeis.org/A262961. Accessed April 2017
Stein, E.M., Weiss, G.: Introduction to Fourier Analysis on Euclidean Spaces. Princeton Mathematical Series, vol. 32. Princeton University Press, Princeton (1971)
Watson, G.N.: A Treatise on the Theory of Bessel Functions, 2nd edn. Cambridge University Press, Cambridge (1944)
Yun, Z.: Galois representations attached to moments of Kloosterman sums and conjectures of Evans. Compos. Math. 151(1), 68–120 (2015), Appendix B by Christelle Vincent
Zhou, Y.: Wick rotations, Eichler integrals, and multi-loop Feynman diagrams. arXiv:1706.08308 [math.NT] (2017)
Acknowledgements
In early 2017, I wrote up this paper in Beijing, mostly drawing on my research notes prepared at Princeton during 2012 and 2013. I thank Prof. Weinan E for arranging my stays in Princeton and Beijing, as well as organizing a seminar on constructive quantum field theory at Princeton. After completion of the initial draft of this article, I received from Dr. David Broadhurst his slides for recent talks [6,7,8] on Bessel moments, which set his conjectures in a wider context. I thank Dr. Broadhurst for his constant encouragements and incisive comments on this project. I am indebted to an anonymous referee for thoughtful suggestions on improving the presentation of this paper. In January 2013, I benefited from fruitful discussions with Prof. Jon Borwein on his previous contributions to Bessel moments and elliptic integrals; I was equally grateful to his friendly communications on my then-unpublished work related to Hilbert transforms. I dedicate this work to his memory.
Author information
Authors and Affiliations
Corresponding author
Additional information
To the memory of Jonathan M. Borwein (1951–2016)
This research was supported in part by the Applied Mathematics Program within the Department of Energy (DOE) Office of Advanced Scientific Computing Research (ASCR) as part of the Collaboratory on Mathematics for Mesoscopic Modeling of Materials (CM4).
Rights and permissions
About this article
Cite this article
Zhou, Y. Hilbert transforms and sum rules of Bessel moments. Ramanujan J 48, 159–172 (2019). https://doi.org/10.1007/s11139-017-9945-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11139-017-9945-y