New general mixed-integer linear programming model for mobile workforce management

Abstract

A mathematical model is introduced to solve a mobile workforce management problem. In such a problem there are a number of tasks to be executed at different locations by various teams. For example, when an electricity utility company has to deal with planned system upgrades and damages caused by storms. The aim is to determine the schedule of the teams in such a way that the overall cost is minimal. The mobile workforce management problem involves scheduling. The following questions should be answered: when to perform a task, how to route vehicles—the vehicle routing problem—and the order the sites should be visited and by which teams. These problems are already complex in themselves. This paper proposes an integrated mathematical programming model formulation, which, by the assignment of its binary variables, can be easily included in heuristic algorithmic frameworks. In the problem specification, a wide range of parameters can be set. This includes absolute and expected time windows for tasks, packing and unpacking in case of team movement, resource utilization, relations between tasks such as precedence, mutual exclusion or parallel execution, and team-dependent travelling and execution times and costs. To make the model able to solve larger problems, an algorithmic framework is also implemented which can be used to find heuristic solutions in acceptable time. This latter solution method can be used as an alternative. Computational performance is examined through a series of test cases in which the most important factors are scaled.

1 Introduction

The mobile workforce management problem in question has characteristics from both scheduling and vehicle routing problems. Scheduling problems arise when some activities must be carried out, but the sequence and timing of the required steps, usually called tasks, are to be decided. A wide range of scheduling problems appears in the industry, which are usually given by the recipe of the process and an objective. The most common objectives are the minimization of processing time, i.e. the makespan, the minimization of costs, or the maximization of the throughput or profit over a fixed time horizon. Vehicle routing problems (VRP) can be regarded as generalizations of the travelling salesman problem (TSP). In a TSP, a set of nodes must be visited by the same actor with minimal transportation effort. In a VRP, there are multiple such actors sharing the work, and the overall goal can be more complex. These problems are difficult on themselves, and were subject to various, mostly heuristic solution methods, each focusing on some specific problem class.

The literature review to be presented has three main parts: the first part focuses on scheduling, the second part on VRP, and the third part on specific mobile workforce problem definitions, solution approaches and case studies.

1.1 Scheduling problems

Scheduling focuses on timing several activities, usually called tasks. With the exception of some special problem classes, scheduling can be an NP-hard problem, requiring heuristic methods to tackle. For instance, flow shop scheduling with multiple machines is already falling into this category (Osman and Potts 1989). There are heuristic, combinatorial and mathematical programming approaches as well. Among the heuristic approaches are the Simulated Annealing (SA) used for job shop scheduling (Raaymakers and Hoogeveen 2000), and Genetic Algorithm (GA) applications (Bierwirth and Mattfeld 1999). The common advantage of these methods is that they are able to consider a very large search space, a disadvantage is the specificity and lack of global optimality. A combinatorial approach for scheduling is, for example, the S-Graph framework, which can handle different storage policies in batch process scheduling (Romero et al. 2004), or timing constraints between tasks as well (Hegyhati et al. 2011). The framework can also be enhanced by mathematical programming tools (Lainez et al. 2010).

Mathematical programming methods are popular either alone or as part of an algorithmic framework for a range of problems, including scheduling. A good compromise between modelling power and computational complexity is the class of Mixed-Integer Linear Programming (MILP), which is widely used. Mendez et al. (2006) provided a state-of-the-art review on different MILP modelling approaches. Although the shown approaches focus on batch processes, the MILP modelling techniques can be easily adapted to different contexts, which is a strong advantage of mathematical programming in general. In the model development point of view, MILP approaches either use some concept of time points or time slots (Pinto and Grossmann 1995), or the precedence relationship between tasks (Mendez and Cerda 2003) to define the key decision variables. One property of mathematical programming approaches is the possibility of equivalent, but technically easier model formulations. This had been demonstrated particularly for scheduling problems (Sahinidis and Grossmann 1991). Therefore, the choice of decision variables is a critical part of model development. Kim et al. (2000) proposed a slot-based approach for a multipurpose scheduling problem dealing with different storage methods. Bradac et al. (2015) used an MILP model based on time slots for the scheduling of domestic appliances subject to time-based energy prices and user preferences, suggesting that time slots can be a useful technique for other purposes.

1.2 Vehicle routing problems

In VRP problems, the main decisions are the assignment of sites to vehicles, and the visit order of sites by the assigned vehicles. The problem may involve other constraints and features, for example time windows for visits, precedence relationships, resource capacity, and multiple depots. A recent review by Vidal et al. (2020) provides an insight into the wide range of possible real-life considerations for VRP case studies.

Standalone MILP solutions were developed for different classes of both the TSP and the more general VRP problems, including problems with multiple vehicle depots (Kulkarni and Bhave 1985). A wide range of generic algorithmic improvements were proposed to traverse the search space of models for VRP problems faster (Costa et al. 2019). However, due to computational complexity, a more common approach is the consideration of an algorithmic framework that is only based on a mathematical programming model, but controls the traverse of the search space on its own.

Transportation efforts are a key factor in VRP problems, usually expressed in terms of time or costs. Travelling efforts can be estimated a priori, and in some scenarios, may depend on current vehicle load. Camm et al. (2017) proposed a solution to the VRP problem where distances to be travelled are weighted by passengers on board. The authors first formulate the problem as an MILP, then solved it by a specific algorithmic framework. Chitty and Hernandez (2004) applied the Ant Colony Optimization method (ACO) for minimizing the total mean time and variance of vehicles.

Time windows for the vehicles arriving at certain sites are a common extension for VRP problems. A common scenario is when products with a limited lifespan have to be delivered. In these cases, production is usually part of the decision problem together with routing. Chen et al. (2009) proposes a solution for VRP with time windows for perishable products by a nonlinear programming model, which is then solved by an adaptation of the Nelder-Mead method. Geismar et al. (2008) addressed a similar problem with a GA framework. Kergosien et al. (2017) formulated an MILP model for chemotherapy production and delivery. In this scenario, although only a single vehicle was used multiple times, the model turned out computationally costly and the authors applied the Benders decomposition method (Benders 1962) to solve it. Lee et al. (2014) formulated an MILP for a similar problem of nuclear medicine delivery, and the algorithmic framework was the Large Neighborhood Search (LNS) in their case. Ben Abdelaziz et al. (2017) proposed a stochastic programming approach for a VRP when passenger transport had to be organized from various points by airport buses. Their model also considered desired timing constraints for each passenger group. Gong et al. (2012) showed that the Particle Swarm Optimization method (PSO) can also be used to solve VRP problems with time windows. Another common extension for VRP problems is vehicle capacity, which limits the routes possible to a single vehicle. Liu et al. (2017) proposed a Tabu Search method for the effective solution of VRP where both vehicle capacities and timing constraints were considered. The authors proposed a Lagrangian relaxation for larger problem instances.

The increasing popularity of electric vehicles and other alternative delivery technologies also had an impact on research towards VRP. Current electric vehicles usually have a relatively short capacity, and their routes have to be designed accordingly. Pelletier et al. (2019) proposed a solution for VRP of electric vehicles with uncertain data. Macrina et al. (2019) considered the VRP with time windows for a fleet of conventional and electric vehicles. The authors apply a variant of the Large Neighborhood Search heuristic based on an MILP model. Paz et al. (2018) solved the VRP problem involving electric vehicles with a standalone MILP model, which also takes multiple depots, time windows, and different battery technologies into consideration. The model was tested on small scale problem instances with few vehicles and sites. Wang et al. (2017) considered the problem of VRP with available drones as an alternative for using trucks only for product delivery. An MILP-based approach was also proposed which used a Branch and price algorithm (Wang and Sheu 2019).

1.3 Mobile workforce management

Mobile workforce is needed to be managed in many areas, including product delivery, maintenance of spatially distributed infrastructure, and any kind of service that involves travelling to clients (Castillo-Salazar et al. 2016). Working personnel must travel to one or multiple sites in some order and must also perform tasks, therefore both routing and scheduling decisions are made. The spreading and evolution of communication tools introduce new possibilities for monitoring and managing mobile workforce (Bakewell et al. 2018). Nevertheless, there is a huge potential in optimizing workforce management for existing businesses. Mobile workforce management problems in this sense do not have a strict formal definition which clearly distinguishes them from VRP—in fact, the main solution approaches are similar. Instead, these problems are characterized by the importance of tasks to be executed by the workforce. For example, tasks usually take a considerable amount of time. In some cases, a complex activity is modelled as a set of different tasks, the execution of which are usually related. Nevertheless, routing decisions that determine travelling efforts are still an important factor in decision making.

Dependency of tasks on each other is a common trait of workforce scheduling problems. Precedence is the most common example of such a relation between tasks, which requires particular pairs of tasks to be executed in a given order. As constraints, precedence can appear in simpler problems like TSP as well (Sung and Jeong 2014). In the modelling point of view, the vast majority of mathematical programming approaches exploit the precedence of tasks at different sites as decision variables. Also, standalone mathematical programming approaches are uncommon. Instead, MILP models can be effectively included in algorithmic frameworks, as the integer decision variables can be assigned by heuristics as well (Goel and Meisel 2013). A mobile workforce management problem with precedence relationships were solved by Pereira et al. (2020) with an ACO solution approach, which was based on an MILP model. The authors remark that the presence of dependencies between tasks often make local neighbourhood search methods difficult to implement.

Goel et al. (2010) proposed an MILP model for scheduling mobile workforce, where time windows and precedence relations are simultaneously considered, and suggested an iterative solution algorithm. Starkey et al. (2016) defined the mobile workforce management problem as grouping places into worker areas served independently by travelling engineers, motivated by the telecommunications field. The proposed solution involves genetic algorithms and fuzzy logic. In a more recent work, a similar approach is presented to address the question when to optimize and rearrange existing worker areas (Chimatapu et al. 2018).

The vehicles may have different properties, for example due to team member expertise differences. Decision on how the teams can be formed based on individual skills is on itself a hard problem which requires heuristic methods (Starkey et al. 2018). The workforce management of an electricity utility company was considered by Çakırgil et al. (2020). Their model involves different skills, multiple depots and two concurrent objectives of weighted total time and execution costs. The proposed solution involves a multi-stage heuristic that relies on an MILP model.

It can be observed that mobile workforce applications usually specialize in the single case study which had to be solved, and the corresponding heuristic algorithms are designed accordingly. Standalone MILP, or general algorithmic approaches are usually proposed to more general problem classes. The aim of this work is to present an MILP approach that can be used either as a standalone solution or as part of an algorithmic framework. A key feature of the model is that the slot-based decision variables are applied instead of precedence-based decisions, which are the more common for VRP case studies. This choice makes a wide range of features possible to be easily modelled, including time windows, vehicle capacities, resource usage, different vehicle efficiencies, and multiple kinds of relations between tasks. To our best knowledge, there is neither a slot-based MILP approach in the literature specific to mobile workforce management, nor one which supports the aforementioned features in a single model. A previous work was dedicated to the possible options of the algorithmic framework for mobile workforce management (Eles et al. 2018). In this work, the MILP model is proposed for scheduling and routing of mobile workforce, which can be used alone or as part of an algorithmic framework. The capabilities of both methods were thoroughly investigated.

The rest of the paper is structured as follows. The second section describes the problem formulation with an example motivational problem and its solution shown. The third section presents the MILP model in detail, and the fourth section presents the algorithmic framework. The case study regarding the standalone MILP and the algorithmic solution approaches are discussed in the fifth and sixth section, respectively.

2 Problem specification

In this section the mobile workforce management problem is described which can be regarded as mix of traveling salesman problem (how to visit the sites) and scheduling problem (when each task should be performed). The assumptions made for each component of the real-world problem in order to formulate our model are also listed.

The scope of the problem governs a single workday of a company responsible for executing tasks arising in various locations. An illustrative example for this scenario could be a public service company which executes maintenance jobs and repairs on-demand. The tasks take place at different points of the infrastructure (e.g., the power grid). Nevertheless, the formulation is intended to be more general.

The company has several working teams which can be assigned to the jobs. These teams start at their depot at the beginning of the day, must travel to the tasks, execute them one by one, and then return to their depot by the end of the workday. Briefly, the company has to decide for each team what tasks to do, in which order, and at what exact times (see Fig. 1), subject to a broad range of restrictions. A motivational example which serves as a demonstration for the problem specification is included in the case study.

Fig. 1

Illustration of the goal of the optimization problem: given a set of tasks, decide on the precise timetable of the teams for a single workday

2.1 Objective and scope of optimization

The objective function is cost minimization where all tasks are mandatory. Therefore, the list of tasks is treated as parameter to the problem and is not subject to decision making.

This is due to practical considerations. Skipping a critical repair job is not allowed for a utility company and the original problem definition is motivated by this scenario. The decision about non-urgent maintenance tasks is made on a higher level, usually by the management, which is out of scope of our target problem.

Note that, as will be shown, the cost functions can be used to express a difference for the same task being executed in different situations.

2.2 Task scheduling

The key question is how task execution is performed. In short, each task must be assigned to one team. The problem involves decision about how to make these assignments. The following assumptions are made.

• Teams are fixed.

• Task execution cannot be interrupted once started (non-preemptive execution).

• Task execution takes a fixed amount of time and cost, both depending on the team chosen.

Teams execute tasks by visiting their sites one by one. If the team executes two tasks consecutively on different locations, travelling has to be taken into account. Teams also travel from the depot to their first task, and from their last task back to the depot. Therefore, a team's schedule for a workday consists of working on tasks and travelling between locations. Assumptions about travelling are the following:

• A task is located at a single location, called task site.

• Multiple tasks may be located at the same site.

• Distances of the sites are given as a parameter.

• Travelling time and costs are proportional to distance. Teams have their own average speed and cost ratio given as parameters.

Teams also have a limited working capacity in three different aspects: the total time travelled, the total distance travelled, and the total time spent in duty are all limited by an upper constant each, specific for each team. Just before and after executing a task, a team may perform several additional activities, one at a time. See Fig. 2 for the complete list in logical order, more about these later.

Fig. 2

Possible activities a team may perform before and after executing a task

2.3 Packing and unpacking

Our problem formulation includes special activities called packing and unpacking. These represent preparations and post-work that are performed once when teams execute one or more tasks in a row at the same site. The rules describing how packing and unpacking activities work are the following.

• If a team arrives to a task site, an unpacking activity must be performed.

• Unpacking is not performed if the previous task is at the same site.

• If a team leaves a task site, a packing activity must be performed.

• Packing is not performed if the next task is at the same site.

• Packing and unpacking costs and times are fixed, and specific for the team.

2.4 Time windows

Although all tasks are mandatory, the exact time of execution may affect costs, or can be subject to restrictions. For this reason, time windows are introduced in the problem formulation. Two different kinds of time windows are assumed: absolute and expected (see Fig. 3).

• An absolute time window is a time interval, which must wholly contain the execution of the task.

• An expected time window is a time interval, which should contain the execution of the task, but it is allowed to be violated for a specific cost. Both starting a task earlier than the window, and finishing a task later than the window incurs cost proportional to the extent of earliness or lateness. The two cost factors are specific for the task.

• Each task may have its own absolute and expected time window independently, provided as parameters.

Fig. 3

Absolute and expected time windows

2.5 Resource management

Task execution may require additional kinds of resources from teams, independent of previously mentioned times and costs. The assumptions on resources are the following.

• Each task has a requirement for each resource, given as a parameter. The exact amount depends on both the task and the team selected.

• Each team has its own maximum capacity for carrying an amount of each resource.

• Each resource has a maximum capacity for the workday, shared among all teams.

• Each resource has a proportional cost of usage.

There are two kinds of resources considered: consumables and tools. Consumables are used up in a single task, but tools can be used any number of times. That implies, the total amount of a resource needed for multiple tasks is a sum for a consumable, and a maximum for a tool resource (see Fig. 4).

Fig. 4

Illustration of consumable and tool resource utilization for one team

2.6 Pairwise task relations

The problem formulation also allows tasks to be dependent on each other. Relations between particular pairs of tasks can be defined, which impose additional constraints on the execution of the two tasks. Let K₁ and K₂ be two different tasks. The relations that can be defined on K₁ and K₂ are the following (see Fig. 5).

• Free precedence: K₂ must start after K₁ finished.

• Same-team precedence: free precedence, also requiring K₁ and K₂ to be executed by the same team.

• Protected precedence: free precedence, also requiring security measures between K₁ and K₂ (see later).

• Mutual exclusion: execution times of K₁ and K₂ may not overlap.

• Parallel execution: K₁ and K₂ are executed in parallel by two adequate teams simultaneously. Execution starts at the same time and ends according to the longer of the two task execution times.

Fig. 5

Illustration of possible relations between tasks

Protected precedence is intended to model situations where two activities must be performed one after the other on the same site by different teams. Leaving the site unattended can be hazardous, e.g. in case of unfinished roadworks, electric boxes. Two options are available:

• The team executing K₁ may wait until the team executing K₂ arrives.

• The team executing K₁ may perform a closing activity and leave the site. The team executing K₂ must first perform an opening activity. Both the closing and opening activity has a fixed cost and time requirement.

3 MILP model formulation

A Mixed-Integer Linear Programming model was designed to address the problem of mobile workforce management described in the previous section.

The model was developed in GNU MathProg modelling language, as a single MILP model file. Problem data consisting all the required parameters must be provided through one or more data files. The model can be solved with a general-purpose MILP solver in a single call. From now on, we refer to the model as the Standalone MILP, which consists of the constraints and the objective to be presented in this section. The groups of constraints correspond to main components of the problem specification. Variables are denoted by lowercase, parameters and sets are denoted by uppercase symbols. The complete list can be found in the nomenclature.

Since the problem is quite complex, it is unlikely that a purely MILP-based solution can find a globally optimal solution fast in the general case. Therefore, the aim in model design was to easily support the widest range of features, so that the MILP can be utilized in various heuristic optimization algorithms in the future. The selection of the binary decision variables also reflects this purpose, because it is technically easy to preset some variables and solve the model in a reduced search space.

3.1 Key decision variables

The MILP model developed—in contrast to most literature examples for VRP and mobile workforce management problems—is not a precedence-based but a slot-based model. This is characterized by the main decision variables in the model. Slots allow a more straightforward definition of other decision variables and implementing other modelling features, as well as an algorithmic framework afterwards.

For each team, a predefined set of “job slots” is introduced. Job slots are numbered for each team, and a job slot is a placeholder for a single task. Each task must be assigned to a single job slot, but a job slot may remain unused, meaning there is no task assigned. The assignment of tasks to job slots is the core of the decision problem, as it determines which tasks a team must perform, and in what order.

Also, a set of “travelling slots” is also introduced for each team. These are placeholders for possible travelling between two tasks, at the beginning and at the end of the workday. Travelling and job slots of a team are alternating after each other.

Finally, for modelling purposes, the term “site slot” is also introduced. These are simply all job slots, plus the time point of the beginning, and the time point of the ending of the workday, numbered accordingly. Site slots serve as points in time where an exact position of a team is in question. These are helpful because all travelling slots, including the very first and very last one, are now surrounded by two site slots, allowing uniform constraint definitions for travelling slots.

In Fig. 6, the scheme of all slot concepts is illustrated. The team is named $m$, and it has a predefined number of ${N}_{m}$ job slots, where ${N}_{m}$ is a parameter to be decided a priori in the model. However, after solving the problem, team $m$ might only execute some $L$ tasks out of the possible ${N}_{m}$, therefore some slots remain unused. Note that even more travelling slots can be unused, depending on how many tasks $m$ executes at the same place consecutively.

Fig. 6

Slot concepts in the MILP model. Team $m$ has ${N}_{m}$ predefined job slots, but only executes $L$ tasks in the end

From now on, the $i$ ^th job slot of a team $m$ is denoted by the ordered pair $\left(m,i\right)$, starting by $i=1$. The set of all job slots is ${J}^{slots}$, and the set of all tasks is $K.$ Based on job slots, we can now define the core binary decision variables in the model. These are the assignment variables ${a}_{k,m,i}$, where the index $k\in K$ stands for a task, and $\left(m,i\right)\in {J}^{slots}$ stand for a job slot. The value of ${a}_{k,m,i}$ is 1, whenever task $k$ is assigned to job slot $\left(m,i\right)$, and 0 otherwise. Note that in the motivational example, there was 2 teams and 8 tasks, 8 job slots for each team. This results in $8\cdot 2\cdot 8=128$ binary variables and theoretically covers all possible cases.

An example is provided in Fig. 7 to demonstrate the meaning of variable ${a}_{k,m,i}$ with a small example of 2 teams Team₁ and Team₂, and 3 tasks K_A, K_B and K_C. In the example shown, there are 3 predefined job slots for both teams, and Team₁ uses 1, Team₂ uses 2 of them. From the resulting 18 binary variables, only three take the value 1, which are ${a}_{KA,Team\mathrm{2,1}}$, ${a}_{KB,Team\mathrm{2,2}}$ and ${a}_{KC,Team\mathrm{1,1}}$.

Fig. 7

Example usage of assignment variables ${a}_{k,m,i}$, which represent the core decisions in the model

Variables ${a}_{k,m,i}$ determine the routing decisions. The rest of the decision variables define he exact timing of events, resource usages, costs incurred, and some other decisions. It is notable that most binary decision variables can be (and are) directly calculated from the variables ${a}_{k,m,i}$, and therefore those variables can possibly be left continuous in the model implementation. The two exceptions for this are the binary variables for mutual exclusions and protected precedence relations, as they involve a further discrete decision.

From now on, constraints of the model are presented grouped by the main logical parts.

3.2 Allocation constraints

Allocation constraints are responsible for the basic logic of assignment of tasks to job slots, which are the core decisions in the model. The positions of tasks at starting and ending points of time slots are also determined here.

3.2.1 Assignment of tasks

Task $k$ is assigned to team $m$ (denoted by ${a}_{k,m}^{task}$) if and only if it is assigned to a single job slot $\left(m,i\right)$ of team $m$. As variable ${a}_{k,m}^{task}$ is binary, Constraint (1) also implicitly ensures that at a task is assigned to at most one job slot of a particular team $m$.

$$a_{k,m}^{task} = \mathop \sum \limits_{{\left( {m,i} \right) \in J^{slots} }} a_{k,m,i} \quad\forall k \in K, m \in M$$

(1)

Constraint (2) ensures that all tasks $k$ are assigned to exactly one team. For a particular task $k$, exactly one of the variables ${a}_{k,m}^{task}$ for all $m$ must be 1 and the rest must be 0 to satisfy the equation.

$$1 = \mathop \sum \limits_{m \in M} a_{k,m}^{task} \,\forall k \in K$$

(2)

3.2.2 Positions of teams

Job slots are used consecutively from the first one ($i=1$) and cannot be skipped unless there are no other tasks assigned to further job slots. This can be interpreted in the following way: if a job slot $\left(m,i\right)$ is used and a task is assigned to it, then so does the previous job slot $\left(m,i-1\right)$, expressed in Constraint (3).

$$\mathop \sum \limits_{k \in K} a_{k,m,i - 1} \ge \mathop \sum \limits_{k \in K} a_{k,m,i} \forall \left( {m,i} \right) \in J^{slots} : i > 1$$

(3)

Binary variable ${b}_{m,i,s}^{present}$ denotes whether the exact position of $m$ at job slot (or site slot) $\left(m,i\right)$ is site $s$ or not. All values of ${b}_{m,i,s}^{present}$ are directly calculated now by constraints (4–7).

At the beginning, when the first travelling slot $\left(m,0\right)$ of team $m$ is started, the team $m$ is at its starting depot. In the end of the workday, which is at the end of travelling slot $\left(m,{N}_{m}\right)$, at time point $\left(m,{N}_{m}+1\right)$, it is at its final depot.

$$b_{{m,0,S_{m}^{start} }}^{present} = 1\, \forall m \in M$$

(4)

$$b_{{m,0,S_{m}^{end} }}^{present} = 1\, \forall m \in M$$

(5)

At the beginning of each job slot $\left(m,i\right)$ of a team $m$, the team is present at the task execution site $s$ if and only if a task $k$ whose site is ${S}_{k}^{task}=s$ is assigned to the job slot $\left(m,i\right)$.

$$b_{m,i,s}^{present} = \mathop \sum \limits_{{k \in K:S_{k}^{task} = s}} a_{k,m,i} \,\forall \left( {m,i} \right) \in J_{slots} , s \in S_{tasksites}$$

(6)

Finally, Constraint (7) ensures that the team is in exactly one position throughout the day, which can be a depot or a task site.

$$\mathop \sum \limits_{{s \in S_{tasksites} \cup \left\{ { S_{m}^{start} ,S_{m}^{end} } \right\}}} b_{m,i,s}^{present} = 1 \,\forall \left( {m,i} \right) \in S_{slots}$$

(7)

Throughout this work, we assumed that vehicles return where they started, ${S}_{m}^{start}={S}_{m}^{end}.$ If this is the case, Constraints (4–7) well-define values of ${b}_{m,i,s}^{present}$, even if this variable is continuous.

3.3 Travelling and continuity constraints

There is a set of constraints that establish the connection between consecutive tasks of the same team. These constraints make sure that the travelling times, costs and possible idle times are managed correctly, as well as the continuity of the alternating travelling and job slots, and some global limitations for the teams.

3.3.1 Movement between sites

Binary variables ${b}_{m,i,{s}_{1},{s}_{2}}^{sch}$ denote movement between sites ${s}_{1}$ and ${s}_{2}$ in a travelling slot, while ${b}_{m,i}^{travel,move}$ denotes if there is any movement. These must be forced to be 1 whenever needed.

Constraint (8) expresses that for all travelling slots $\left(m,i\right)$, and pairs of different sites ${s}_{1}$ and ${s}_{2}$, there is a movement between these two sites in this travelling slot if team $m$ is at ${s}_{1}$ at the beginning, and at ${s}_{2}$ at the end of travelling slot $\left(m,i\right).$ These two events are referred by site slots $\left(m,i\right)$ and $\left(m,i+1\right)$, respectively.

$$b_{{m,i,s_{1} ,s_{2} }}^{sch} \ge b_{{m,i,s_{1} }}^{present} + b_{{m,i + 1,s_{2} }}^{present} - 1 \,\forall \left( {m,i} \right) \in T_{slots} , s_{1} ,s_{2} \in S: s_{1} \ne s_{2}$$

(8)

There is movement in travelling slot $\left(m,i\right)$ if and only if there are two sites ${s}_{1}$ and ${s}_{2}$ between which the movement occurs. Constraint (9) expressing this fact is an equation, because there can only be one such $\left({s}_{1},{s}_{2}\right)$ pair.

$$b_{m,i}^{travel,move} = \mathop \sum \limits_{{s_{1} ,s_{2} \in S:s_{1} \ne s_{2} }} b_{{m,i,s_{1} ,s_{2} }}^{sch} \,\forall \left( {m,i} \right) \in T_{slots}$$

(9)

Distance between sites travelled is determined similarly in Constraint (10). For each pair of sites, their distance is taken into account as a factor to determine the total distance travelled by team $m$ in its travelling slot $\left(m,i\right)$.

$$d_{m,i} = \mathop \sum \limits_{{s_{1} ,s_{2} \in S:s_{1} \ne s_{2} }} b_{{m,i,s_{1} ,s_{2} }}^{sch} \cdot D_{{s_{1} ,s_{2} }} \,\forall \left( {m,i} \right) \in T_{slots}$$

(10)

3.3.2 Slot continuity

It must be ensured that job slots have a nonnegative length (even if they are out of use). This can be done by the Constraint (11), since the job slot $\left(m,i\right)$ starts when travelling slot $\left(m,i-1\right)$ ends, and ends when travelling slot $\left(m,i\right)$ starts.

$$t_{m,i}^{travel,start} \ge t_{m,i}^{travel,end} \,\forall \left( {m,i} \right) \in J_{slots}$$

(11)

The nonnegative length of travelling slots is implicitly guaranteed by their length formula, expressed by Constraint (12). Travelling slot $\left(m,i\right)$ consist of travelling time, depending on distance ${d}_{m,i}$ and team speed ${V}_{m}$, packing and unpacking time, and idle time. If there is no movement in this travelling slot, only idle time may occur.

$$t_{m,i}^{travel,end} - t_{m,i}^{travel,start} = \frac{{d_{m,i} }}{{V_{m} }} + b_{m,i}^{travel,move} \cdot \left( {T_{m}^{pack} + T_{m}^{unpack} } \right) + t_{m,i}^{idle}$$

(12)

$$\forall \left( {m,i} \right) \in T_{slots}$$

3.3.3 Team limitations

Constraints (13–15) ensure global limitations for the teams.

For each team $m$, the total travelling time has an upper limit ${T}_{m}^{travel,MAX}$. For all job slots $(m,i)$, travelling times without idle and packing times are added up against this limit.

$$\mathop \sum \limits_{{\left( {m,i} \right) \in T^{slots} }} \left( t_{m,i}^{travel,end} - t_{m,i}^{travel,start} \right) \le T_{m}^{travel,MAX} \,\forall m \in M$$

(13)

Total time in duty including any activities is also bounded by a parameter ${T}_{m}^{work,MAX}$, for each team $m$.

$$t_{{m,N_{m} }}^{travel,end} - t_{m,0}^{travel,start} \le T_{m}^{work,MAX} \,\forall m \in M$$

(14)

The total distance travelled, which is the sum of actual distances ${d}_{m,i}$, is also limited by a parameter ${D}_{m}^{travel,MAX}$.

$$\mathop \sum \limits_{{\left( {m,i} \right) \in T^{slots} }} d_{m,i} \le D_{m}^{travel,MAX}\, \forall m \in M$$

(15)

3.4 Task execution constraints

In a job slot, several events may happen before, during, and after a task is executed. This set of constraints is responsible for calculating timings and costs of task execution, and possible preconditions for them. A common property of these constraints is that they are formulated for all tasks $k\in K$.

3.4.1 Job slot sequencing

The start of the presence of team $m$ at site for executing task $k$, denoted by ${t}_{k}^{presence,start}$, takes place at the beginning of some job slot $(m,i)$ of a team $m$ the task is assigned to. Constraint (16) formulates this fact for all possible allocations ${a}_{k,m,i}$ as a big-M constraint.

$$\begin{gathered} t_{k}^{presence,start} - t_{m,i - 1}^{travel,end} \ge \left( { - 1} \right) \cdot T^{WORKDAY} \cdot \left( {1 - a_{k,m,i} } \right) \hfill \\ t_{k}^{presence,start} - t_{m,i - 1}^{travel,end} \le \left( { + 1} \right) \cdot T^{WORKDAY} \cdot \left( {1 - a_{k,m,i} } \right) \hfill \\ \forall k \in K, \left( {m,i} \right) \in J_{slots} \hfill \\ \end{gathered}$$

(16)

After the team is present at the site, nonnegative waiting and site opening times may take place before the task execution begins. Site opening depends on choices made at protected precedence relations, which will be discussed later. The final value in Constraint (17) is ${t}_{k}^{start}$, the actual starting time of execution.

$$t_{k}^{presence,start} + t_{k}^{wait,before} + p_{k}^{open} \cdot T_{k}^{open} = t_{k}^{start}\, \forall k \in K$$

(17)

The net execution time is the time between the starting time (${t}_{k}^{start}$) and ending time (${t}_{k}^{end}$). This depends on team selection, so summed for each allocation candidate ${a}_{k,m}^{task}$. There is also a nonnegative slack term ${t}_{k}^{slack}$ which relaxes this interval. This is essential for parallel execution of tasks to take place, where the faster team should “wait” for the other one to finish. In reality, the slower team’s working speed is the bottleneck as they work together. Parallel execution relations are also discussed later.

$$t_{k}^{start} + \mathop \sum \limits_{m \in M} \left( {a_{k,m}^{task} \cdot T_{k,m}^{exec} } \right) + t_{k}^{slack} = t_{k}^{end} \,\forall k \in K$$

(18)

After finishing execution, the team may wait additionally, and possibly close the task site due to some protected precedence relation of $k$, similarly to opening sites before execution. Then, presence of the team at the task site ends.

$$t_{k}^{end} + t_{k}^{wait,after} + p_{k}^{close} \cdot T_{k}^{close} = t_{k}^{presence,end}\, \forall k \in K$$

(19)

Finally, the end of presence of team $m$ at site for executing task $k$, denoted by ${t}_{k}^{presence,end}$, happens in the end of job slot $(m,i)$ of some team $m$. The big-M constraint has condition ${a}_{k,m,i}=1$ and coefficient ${T}^{WORKDAY}$, similarly to the constraint for the start of the presence.

$$\begin{gathered} t_{k}^{presence,end} - t_{m,i}^{travel,begin} \ge \left( { - 1} \right) \cdot T^{WORKDAY} \cdot \left( {1 - a_{k,m,i} } \right) \hfill \\ t_{k}^{presence,end} - t_{m,i}^{travel,begin} \le \left( { + 1} \right) \cdot T^{WORKDAY} \cdot \left( {1 - a_{k,m,i} } \right) \hfill \\ \forall k \in K, \left( {m,i} \right) \in J_{slots} \hfill \\ \end{gathered}$$

(20)

3.4.2 Task time windows

There are two kinds of time windows in the model. A task must be executed within its absolute time window $\left[{T}_{k}^{earliest}, {T}_{k}^{latest}\right]$ which must be strictly respected. Also, a task should be executed in its narrower expected time window $\left[{T}_{k}^{expected,start}, {T}_{k}^{expected,end}\right]$, the violation of which is possible in exchange for a penalty cost proportional to the extent of early starting or late ending.

Constraints (21–22) implement absolute time windows. The earliest starting time of a task is the beginning of its absolute time window, a lower bound for task starting time that cannot be violated.

$$T_{k}^{earliest} \le t_{k}^{start} \,\forall k \in K$$

(21)

The latest ending time of a task, similarly, is an upper bound for task ending time.

$$t_{k}^{end} \le T_{k}^{latest}\, \forall k \in K$$

(22)

The expected window can be violated in either direction, with an earliness penalty cost ${C}_{k}^{earliness}$, and lateness penalty cost ${C}_{k}^{lateness}$, expressed in Constraints (23–24). Both are proportional to the extent of the violation. Variable ${c}_{k}^{pen,early}$ and ${c}_{k}^{pen,late}$ denote the penalty costs incurred in these ways. Note that the formulation allows both kinds of penalties to be present at the same time, which might be inevitable when the expected time window is shorter than the task execution time.

If a task starts too early, the penalty cost must be calculated proportional to earliness.

$$\left( {T_{k}^{expected,start} - t_{k}^{start} } \right) \cdot C_{k}^{earliness} \le c_{k}^{pen,early}\,\forall k \in K$$

(23)

If a task ends too late, the penalty cost must be calculated proportional to lateness.

$$\left( {t_{k}^{start} - T_{k}^{expected,end} } \right) \cdot C_{k}^{lateness} \le c_{k}^{pen,late}\, \forall k \in K$$

(24)

Note that neither of the two windows are mandatory. To omit an absolute time window, it must be set to coincide the start and end of the workday. To omit an expected time window, it must coincide the absolute time window. In both cases, the corresponding constraints become redundant.

3.5 Resource management constraints

There are two kinds of resources in the proposed model: consumables, which are used up at tasks, and tools, which must be at hand for the teams.

We are interested in the requirement ${q}_{r,m,i}^{req}$ of resource $r$ in job slot $(m,i)$. As the requirement parameter in a particular assignment ${Q}_{r,k,m}^{req}$ depends on both the task executed and the team, these must be summed for all tasks $k$ multiplied by the allocation variable ${a}_{k,m,i}$. Since at most one task $k$ is assigned to job slot $(m,i)$, the sum yields the desired ${q}_{r,m,i}^{req}$ in Constraint (25).

$$q_{r,m,i}^{req} = \mathop \sum \limits_{k \in K} \left( {a_{k,m,i} \cdot Q_{r,k,m}^{req} } \right)\, \forall r \in R, \left( {m,i} \right) \in J^{slots}$$

(25)

If resource $r$ is a consumable, then for any team $m$ the amount carried is the sum required for the execution of tasks.

$$q_{r,m}^{carry} = \mathop \sum \limits_{{\left( {m,i} \right) \in J^{slots} }} q_{r,m,i}^{req} \,\forall r \in R^{cons} , m \in M$$

(26)

If resource $r$ is a tool, then for any team $m$ the amount carried must be equal or greater than the maximum required for tasks. Note that these constraints do not force the carried amount to be minimal, but the optimization does, because resource utilization has a cost.

$$q_{r,m}^{carry} \ge q_{r,m,i}^{req} \,\forall r \in R^{tool} , \left( {m,i} \right) \in J^{slots}$$

(27)

For each team $m$ and resource $r$, the carried amount is limited by the capacity of team $m$, denoted by ${Q}_{r,m}^{MAX}$.

$$q_{r,m}^{carry} \le Q_{r,m}^{MAX} \,\forall r \in R, m \in M$$

(28)

For each resource $r$, being either a consumable or a tool, the total resource amount utilized by all teams $m$ is limited to the available amount for the company. Constraint (29) expresses this statement. All utilized amounts are summed.

$$\mathop \sum \limits_{m \in M} q_{r,m}^{carry} \le Q_{r}^{CAP} \,\forall r \in R$$

(29)

3.6 Pairwise relations' constraints

In the problem description point of view, pairwise task relations are provided as sets of ordered pairs $\left({k}_{a},{k}_{b}\right)$ of tasks for each kind of relation. These are precedence in general (${P}^{prec}$), same-team precedence (${P}^{same}$), protected precedence (${P}^{prot}$), mutual exclusion (${P}^{mutex}$), and parallel execution (${P}^{parallel}$). Note that the set ${P}^{prec}$ includes free, same-team and protected precedence relations.

3.6.1 Precedence

For any kind of precedence relations $\left({k}_{1},{k}_{2}\right)\in {P}^{prec}$, the ending time of the first task ${k}_{1}$ must precede the starting time of the second task ${k}_{2}$. Constraint (30) expressing this fact implicitly assures that ${k}_{2}$ is done by a different team, or by the same team in a later job slot.

$$t_{{k_{1} }}^{end} \le t_{{k_{2} }}^{start} \,\forall \left( {k_{1} ,k_{2} } \right) \in P^{prec}$$

(30)

For all same-team precedence relations $\left({k}_{1},{k}_{2}\right)\in {P}^{same}$, besides the original precedence relation, the same team must execute the two tasks. Constraint (31) expresses that these two tasks are assigned to any team $m$ exactly in the same case.

$$a_{{k_{1} ,m}}^{task} = a_{{k_{2} ,m}}^{task}\, \forall \left( {k_{1} ,k_{2} } \right) \in P^{same} , m \in M$$

(31)

3.6.2 Protected precedence

Protected precedence relations are more complex, there are two choices for each $\left({k}_{1},{k}_{2}\right)\in {P}^{prot}$. A binary variable ${p}_{{k}_{1},{k}_{2}}^{prot}$ is introduced to denote this choice. If ${p}_{{k}_{1},{k}_{2}}^{prot}=1$, then teams are not waiting for each other, but the team executing ${k}_{1}$ closes the site of ${k}_{1}$ there and leaves, and when the other team arrives to execute ${k}_{2}$, it also opens the site of ${k}_{2}$. The alternative ${p}_{{k}_{1},{k}_{2}}^{prot}=0$ is when the team executing ${k}_{1}$ waits until the second team arrives. Protected precedence relations only have a practical meaning if the tasks are at the same site. Also, it may be theoretically possible that a third team is involved in the procedure, for example, by helping guarding the site, but this possibility is not investigated.

If waiting is chosen (${p}_{{k}_{1},{k}_{2}}^{prot}=0$), then the time (${t}_{{k}_{1}}^{presence,end}$) until the first team is present at the site of task ${k}_{1}$ must follow the time (${t}_{{k}_{2}}^{presence,start}$) when the team for the second task becomes available at its site. The big-M Constraint (32) has condition ${p}_{{k}_{1},{k}_{2}}^{prot}=0$ and coefficient ${T}^{workday}$ and implements case ${p}_{{k}_{1},{k}_{2}}^{prot}=0$. The amount of time ${k}_{1}$ waits if ${p}_{{k}_{1},{k}_{2}}^{prot}=0$ is represented by variable ${t}_{k}^{wait,after}$ in Constraint (19).

$$t_{{k_{2} }}^{presence,start} - t_{{k_{1} }}^{presence,end} \le \left( { + 1} \right) \cdot T^{workday} \cdot p_{{k_{1} ,k_{2} }}^{prot} \,\forall \left( {k_{1} ,k_{2} } \right) \in P^{prot}$$

(32)

If closing and opening is chosen (${p}_{{k}_{1},{k}_{2}}^{prot}=1$), then the fact of closing after ${k}_{1}$ must be indicated in the corresponding binary variable ${p}_{{k}_{1}}^{close}$, like the fact of opening at ${k}_{2}$ in its variable ${p}_{{k}_{2}}^{open}$. These are expressed in Constraints (33–34). Note that variables ${p}_{{k}_{1}}^{close}$ and ${p}_{{k}_{2}}^{open}$ also appear in the job slot sequencing constraints and in the objective, to ensure the time and cost requirement of choice ${p}_{{k}_{1},{k}_{2}}^{prot}=1$.

$$p_{{k_{1} }}^{close} \ge p_{{k_{1} ,k_{2} }}^{prot} \,\forall \left( {k_{1} ,k_{2} } \right) \in P^{prot}$$

(33)

$$p_{{k_{2} }}^{open} \ge p_{{k_{1} ,k_{2} }}^{prot}\, \forall \left( {k_{1} ,k_{2} } \right) \in P^{prot}$$

(34)

It must also be ensured that closing or opening only take place at any task $k$ if it appears in a protected precedence relation where the closing and opening solution is actually chosen.

$$p_{{k_{1} }}^{close} \le \mathop \sum \limits_{{\left( {k_{1} ,k_{2} } \right) \in P^{prot} }} p_{{k_{1} ,k_{2} }}^{prot}\, \forall k_{1} \in K$$

(35)

$$p_{{k_{2} }}^{open} \le \mathop \sum \limits_{{\left( {k_{1} ,k_{2} } \right) \in P^{prot} }} p_{{k_{1} ,k_{2} }}^{prot}\, \forall k_{2} \in K$$

(36)

3.6.3 Mutual exclusion

Mutual exclusion $\left({k}_{1},{k}_{2}\right)\in {P}^{mutex}$ means that two tasks cannot be in progress at any same time. A binary variable ${p}_{{k}_{1},{k}_{2}}^{mutex}$ is introduced to differentiate two possible scenarios for assessing this requirement. Since tasks are mandatory, one of ${k}_{1}$ and ${k}_{2}$ them must be started after the other one is finished. This is expressed by big-M Constraints (37–38) based on the choice of ${p}_{{k}_{1},{k}_{2}}^{mutex}$.

If ${p}_{{k}_{1},{k}_{2}}^{mutex}=1$, then ending time of ${k}_{1}$ is followed by the starting time of ${k}_{2}$.

$$t_{{k_{2} }}^{start} - t_{{k_{1} }}^{end} \ge \left( { - 1} \right) \cdot T^{WORKDAY} \cdot \left( {1 - p_{{k_{1} ,k_{2} }}^{mutex} } \right)\, \forall \left( {k_{1} ,k_{2} } \right) \in P^{mutex}$$

(37)

If ${p}_{{k}_{1},{k}_{2}}^{mutex}=0$, in contrast, starting time of ${k}_{1}$ follows the ending time of ${k}_{2}$.

$$t_{{k_{1} }}^{start} - t_{{k_{2} }}^{end} \ge \left( { - 1} \right) \cdot T^{WORKDAY} \cdot p_{{k_{1} ,k_{2} }}^{mutex}\, \forall \left( {k_{1} ,k_{2} } \right) \in P^{mutex}$$

(38)

3.6.4 Parallel execution

Parallel execution is a model for activities that must be performed as a cooperation between teams, possibly at different sites. The parallel execution relation ensures that starting and ending times coincide.

When tasks ${k}_{1}$ and ${k}_{2}$ must be executed in parallel, $\left({k}_{1},{k}_{2}\right)\in {P}^{parallel}$, both their starting and ending times are synchronized, this is done by Constraints (39–40). Note that this implicitly ensures that the two tasks are done by different teams.

$$t_{{k_{1} }}^{start} = t_{{k_{2} }}^{start} \,\forall \left( {k_{1} ,k_{2} } \right) \in P^{parallel}$$

(39)

$$t_{{k_{1} }}^{end} = t_{{k_{2} }}^{end} \,\forall \left( {k_{1} ,k_{2} } \right) \in P^{parallel}$$

(40)

Note that in many cases a faster and a slower team are considered to execute the two tasks, as parameters ${T}_{k,m}^{exec}$ are generally independent. In this case, the common completion time is always the highest. This is made possible by a nonnegative variable ${t}_{k}^{slack}$, see Constraint (18), which implements job slot sequencing. Variable ${t}_{k}^{slack}$ imposes a phantom waiting time on either team so they could actually finish at the same later time.

3.7 Objective function

The objective in the model is the total cost, which must be minimized. Costs arise for various reasons which are listed below and then summed up.

Travelling costs are calculated from travelled distances, speed, and cost factor for each team.

$$c^{travel} = \mathop \sum \limits_{{\left( {m,i} \right) \in T^{slots} }} \frac{{d_{m,i} }}{{V_{m} }} \cdot C_{m}^{travel}$$

(41)

Packing costs are coming from packing and unpacking for each travelling slot where travelling actually happens. This is also true for moving out and arriving back into the depot.

$$c^{packing} = \mathop \sum \limits_{{\left( {m,i} \right) \in T_{slots} }} \left( {\mathop \sum \limits_{{s_{1} \in S,s_{2} \in S}} b_{{m,i,s_{1} s_{2} }}^{sch} \cdot \left( {C_{m}^{unpack} + C_{m}^{pack} } \right)} \right)$$

(42)

Time window costs are composed of penalties of earliness and lateness from task executions.

$$c^{tw} = \mathop \sum \limits_{k \in K} \left( {c_{k}^{pen,early} + c_{k}^{pen,late} } \right)$$

(43)

Execution costs of tasks are based solely on the team and the task assigned.

$$c^{exec} = \mathop \sum \limits_{k \in K} \mathop \sum \limits_{{\left( {m,i} \right) \in J^{slots} }} \left( {a_{k,m,i} \cdot C_{exec}^{k,m} } \right)$$

(44)

Resource costs are derived from the total amounts used for both consumables and tools.

$$c^{res} = \mathop \sum \limits_{r \in R} \mathop \sum \limits_{m \in M} \left( {q_{r,m}^{carry} \cdot C_{r} } \right)$$

(45)

Opening and closing costs are incurred for each of the closing choices made at protected precedence relations.

$$c^{opcl} = \mathop \sum \limits_{{\left( {k_{1} ,k_{2} } \right) \in P^{prot} }} p_{{k_{1} ,k_{2} }}^{prot} \cdot C_{{k_{1} ,k_{2} }}^{prot,co}$$

(46)

Finally, working time costs are proportional to total times each team spends in duty.

$$c^{work} = \mathop \sum \limits_{m \in M} \left( {t_{{m,N_{m} }}^{travel,end} - t_{m,0}^{travel,start} } \right) \cdot C_{m}^{work}$$

(47)

The objective value is obtained as a sum of components listed above.

$${\text{minimize}}: c^{total} = c^{travel} + c^{packing} + c^{tw} + c^{exec} + c^{res} + c^{opcl} + c^{work}$$

(48)

4 Algorithmic framework

While designing the MILP model, the focus was on the wide range of features it supports, so that heuristic algorithmic solutions could be implemented on them afterwards. Although the Standalone MILP is an option, for large scale problems the model is computationally too difficult. For this reason, an algorithmic framework was implemented which allows us to find heuristic solutions for larger problems in an acceptable amount of time.

4.1 Algorithm description

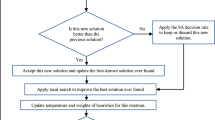
The main idea is to schedule only a single task at once. The algorithm involves five steps:

• Start from the initial solution where no tasks are scheduled yet.

• Choose a new task to be included in the schedule.

• Determine the position of the new task in the schedule.

• Update task timings, resource, cost calculation and other decisions according to the new schedule.

• Repeat Steps 2–4 until all tasks are scheduled.

Steps 2–4 together are called an “iteration” of the algorithm. Each iteration begins with an existing “schedule” of some tasks, and ends with another schedule containing one more task than in the beginning. A schedule consists solely of an ordered list of tasks to execute for each team. In other words, a schedule answers which tasks a team will execute, and in which order, but nothing more specific.

A key characteristic of Step 3 of the algorithm is that the relative order of already scheduled tasks is maintained. That means, the new task is inserted into the list of one of the teams.

Finally, the method for performing an iteration of the algorithm is by the utilization of an MILP model obtained by the modification of the Standalone MILP model. We call this version the Modified MILP model. In short, the Modified MILP model uses the original problem data, plus the already existing schedule as an input, and determines the next schedule as an output. This requires a single MILP execution. Therefore, the involved operations are not even separated. The algorithm is illustrated in Fig. 8.

Fig. 8

In a single step, a new task is selected and inserted into the existing schedule, maintaining relative order of already scheduled tasks. Decision is based on a single run of the Modified MILP model

The Modified MILP is obtained from the Standalone MILP by the following modifications:

• The existing schedule of tasks is added as model input.

• The existing schedule acts as a constraint on the execution.

• The restriction of all tasks being mandatory no longer applies.

• Instead, only the tasks from the existing schedule are mandatory, plus exactly one additional task must also be executed.

Although the Modified MILP model contains more variables and constraints, its search space is significantly reduced. This makes the modified version fast to solve, even multiple times in a row as the algorithm proceeds. Meanwhile, the MILP model still maintains the constraints about timing, resources, and costs. Therefore, the final run of the Modified MILP model scheduling the last task results in a detailed, cost-optimal solution for that particular schedule.

The only feature of the Standalone MILP model which is not supported is the usage of pairwise relations. A relation can interfere with the algorithmic framework in unexpected ways. A single step of the algorithm can easily make decisions that later turn out to be infeasible, because relations of unscheduled tasks are ignored. Taking into consideration pairwise relations in the algorithmic framework is subject to future research.

4.2 Modified MILP model

Here the details of the Modified MILP model are presented. At each step of the algorithm, the set of tasks $K$ is split into ${K}^{done}$ and ${K}^{rem}$ denoting tasks in the existing schedule and remaining to be selected from. For all tasks $k\in {K}^{done}$ there is a job slot it is currently assigned to. This job slot is denoted by ${H}_{k}^{slot}\in {J}^{slots}$. The decisions to be made are the following:

• Select a single remaining task $k\in {K}^{rem}$, which is included in the already existing schedule. This decision is represented by a new binary variable ${x}_{k}^{task}$, which has the value of 1 when $k$ is selected.

• Select a team $m$ the new task is assigned to. This decision is represented by a new binary variable ${x}_{m}^{team}$, where the value 1 means that the selected task is included in the existing schedule of team $m$, while the schedules of other teams remain unchanged.

• Select a job slot $\left(m,i\right)\in {J}^{slots}$, where the new task is inserted in the existing schedule. The new binary variable ${x}_{m,i}^{slot}$ represents this decision by a value of 1.

Note that ${x}_{m,i}^{slot}$ also implicitly determines ${x}_{m}^{team}$, but for model representation purposes, it is easier to introduce these three binary decision variables mentioned. For modelling purposes, an auxiliary variable ${y}_{m,i}$ is also introduced, which denotes whether the new task is inserted before already existing travelling slot $\left(m,i\right)\in {T}_{slots}$ or not. Values of ${y}_{m,i}$ are unambiguously determined by values of ${x}_{m,i}^{slots}$ and vice versa.

The MILP model requires a priori the number of job slots as parameter ${N}_{m}$. In the algorithm, each team $m$ has one more job slot than the number of tasks already assigned to $m$. In short, for each $m$, one extra slot is provided for the new task if it is assigned to $m$.

The connection of decision variables and the algorithmic framework is illustrated in Fig. 9. In the example, team $m$ already has a schedule with tasks ${K}_{1}$, ${K}_{5}$, and ${K}_{2}$ in this order, and in the algorithmic step, a decision is made to select new task ${K}_{4}$ and insert it between ${K}_{5}$ and ${K}_{2}$. Note that other teams may be present. The order of tasks selected during the whole algorithm can also be arbitrary.

Fig. 9

Example usage of decision variables in the algorithmic framework

The additional decision variables ${x}_{k}^{task}$, ${x}_{m}^{team}$ and ${x}_{m,i}^{slot}$ should determine the assignment according to the new schedule unambiguously. The rest of the variables and constraints of the original MILP model ensure feasibility like decision on exact timing and resource utilization. Therefore, a new set of constraints is added to the original model to establish the connection of the new decision variables and the assignment decisions in the original formulation. The original Constraint (2) is dropped, because we do not intend to schedule all tasks at once. Besides, the following new constraints are introduced.

No task can be inserted before travelling slot $\left(m,0\right)$ of any team $m$.

$$y_{m,0} = 0 \,\forall m \in M$$

(49)

Insertion before a travelling slot $\left(m,i\right)$ happens if and only if there is also insertion before the previous travelling slot $\left(m,i-1\right)$ or the new task is inserted just in job slot $\left(m,i\right)$. The first two cases are established by Constraints (50) and (51), respectively. Also, ${y}_{m,i}=0$ is enforced by Constraint (52) if neither condition holds. This completes the consistency of auxiliary values ${y}_{m,i}$.

$$y_{m,i} \ge y_{m,i - 1} \,\forall \left( {m,i} \right) \in J^{slots}$$

(50)

$$y_{m,i} \ge x_{m,i}^{slot} \,\forall \left( {m,i} \right) \in J^{slots}$$

(51)

$$y_{m,i} \le y_{m,i - 1} + x_{m,i}^{slot}\, \forall \left( {m,i} \right) \in J^{slots}$$

(52)

Inserting before any travelling slot $\left(m,i\right)$ of team $m$ can be allowed only if team $m$ is selected.

$$x_{m}^{team} \ge y_{m,i} \,\forall \left( {m,i} \right) \in J^{slots}$$

(53)

Any new task candidate $k\in {K}^{rem}$ is assigned to a job slot $\left(m,i\right)$ if and only if $k$ is the selected new task, and $\left(m,i\right)$ is the selected new job slot. Constraints (54) and (55) ensure ${a}_{k,m,i}=0$ if either condition is not met, while Constraint (56) ensures ${a}_{k,m,i}=1$ if both conditions hold.

$$a_{k,m,i} \le x_{k}^{task} \,\forall k \in K^{rem} , \left( {m,i} \right) \in J^{slots}$$

(54)

$$a_{k,m,i} \le x_{m,i}^{slot}\, \forall k \in K^{rem} , \left( {m,i} \right) \in J^{slots}$$

(55)

$$a_{k,m,i} \ge x_{k}^{task} + x_{m,i}^{slot} - 1 \,\forall k \in K^{rem} , \left( {m,i} \right) \in J^{slots}$$

(56)

Tasks $k\in {K}^{done}$ already scheduled must be scheduled again, therefore they must be assigned to exactly one team. On the other hand, new task candidates $k\in {K}^{rem}$ are only scheduled if selected, therefore the sum in that case is exactly ${x}_{k}^{task}$ instead of 1.

$$1 = \mathop \sum \limits_{m \in M} a_{k,m}^{task} \,\forall k \in K^{done}$$

(57)

$$x_{k}^{task} = \mathop \sum \limits_{m \in M} a_{k,m}^{task} \,\forall k \in K^{rem}$$

(58)

It must be ensured that exactly one new task $k\in {K}^{rem}$, one team $m$ for it, and one of its job slots $\left(m,i\right)$ are selected. This is done by Constraints (59–61).

$$1 = \mathop \sum \limits_{{k \in K^{rem} }} x_{k}^{task}$$

(59)

$$1 = \mathop \sum \limits_{m \in M} x_{m}^{team}$$

(60)

$$1 = \mathop \sum \limits_{{\left( {m,i} \right) \in J^{slots} }} x_{m,i}^{slot}$$

(61)

Finally, the position of a task $k\in {K}^{done}$ previously scheduled to job slot $\left(m,i\right)$ is either job slot $\left(m,i\right)$ or $\left(m,i+1\right)$ based on whether the new task was inserted before it or not, denoted by ${y}_{m,i}$. Constraints (62) and (63) enforce this for all tasks $k\in {K}^{done}$ already scheduled, finishing the connection between ${y}_{m,i}$ and the decision variables.

$$y_{m,i} = a_{k,m,i + 1} \,\forall k \in K^{done} : \left( {m,i} \right) = H_{k}^{slot}$$

(62)

$$1 - y_{m,i} = a_{k,m,i}\, \forall k \in K^{done} : \left( {m,i} \right) = H_{k}^{slot}$$

(63)

All other assignment variables can be explicitly set to zero as in Constraint (64) for already scheduled tasks $k\in {K}^{done}$. The only allowed job slots are $\left(m,i\right)$ and $\left(m,i+1\right)$. Note that Constraint (64) is redundant because Constraints (62–63) implicitly assure these decisions, but it is inserted to help the MILP solver at pre-processing.

$$0 = a_{k,m,j} \,\forall k \in K^{done} , \left( {m,j} \right) \in J^{slots} : \left( {m,i} \right) = H_{k}^{slot} \wedge j \ne i \wedge j \ne i + 1$$

(64)

5 Case study for the Standalone MILP model

To demonstrate the usability of the proposed model and the algorithmic framework, a case study was performed, which has two major parts. In the first part, the Standalone MILP model was tested on different problem instances. In the second part, the algorithmic framework involving the Modified MILP model was tested. This section presents the first part involving the Standalone MILP model.

First, a motivational problem instance is presented in detail, with its optimal solution, as a demonstration for the problem specification and the capabilities of the model. This required a single execution of an MILP solver. Afterwards, several test sets are presented, with multiple, slightly different problem instances to demonstrate how some key parameters of the model affect computational complexity.

The model, all problem data and results presented here are available as “MWM model and case studies” supplementary material, see Eles et al. (2020), as source codes and executable format.

5.1 Motivational problem

In this example problem, a company is responsible for the infrastructure of public lighting and traffic signals.

By the beginning of the working day, 8 mandatory maintenance tasks are reported, named K_1a, K_1b, K_1c1, K_1c2, K_1d, K₂, K_3a, and K_3b. These tasks must be executed between 8:00 and 16:00, and are located at three different sites on the map, named S₁, S₂, and S₃, the first digit in the index of tasks refer to the site. The company has two working teams for these tasks, named Team₁ and Team₂, who are stationed at depot site D in the beginning, and should get back there until the end of the workday. Note that in a general problem, teams may be at different starting depots. The positions are depicted in Fig. 10. The distance between sites is assumed to be the Manhattan-distance, which is calculated between any points ${P}_{1}\left({x}_{1},{y}_{1}\right)$ and ${P}_{2}\left({x}_{2},{y}_{2}\right)$ by the formula $\left|{x}_{1}-{x}_{2}\right|+\left|{y}_{1}-{y}_{2}\right|$.

Fig. 10

Geographic positions of sites, with corresponding tasks in parentheses, and depot with teams

Teams have different properties, but both work for 60 EUR/hour, regardless of activities they make. Team₁ is lightweight, having a speed of 75 km/h and move for 0.4 EUR/km, and doing each task in 45 min. The cost of a task, if done by Team₁, is 100 EUR. Team₂ operates with heavier machinery and therefore work faster, although all other traits are worse. They have a speed of 50 km/h and movement cost of 0.9 EUR/km, and doing each task in 30 min. The cost of a task, if done by Team₂, is 150 EUR. Note that the problem specification would allow distinct execution costs and times for each team and each task, but in this example, both teams see tasks as equally difficult. The specification would also allow limits for total time in duty, total travelled time and distance, but these were omitted in the example.

The next part of the problem formulation is packing and unpacking. These represent the teams setting the scene ready for working and cleaning up afterwards, regardless of the number of tasks executed. Both packing and unpacking can have a unique cost and time requirement for each team separately. In the motivational example, both packing and unpacking costs 10 EUR and takes 10 min.

Absolute and expected time windows can be set for each task, but in the motivational example, only task Kb1 has an absolute time window of 10:00 to 13:00, and an expected time window of 11:30 to 12:30. The reason behind a time window can be an external co-operator or a client only available in this interval. Task execution must fit inside the absolute time window, but it may start earlier, or end later than the beginning and ending of the expected time window. Violating the expected time window in either direction incurs a very high proportional cost of 600 EUR/hour.

Resource utilization is also present in the example problem. For demonstration purposes, there is one consumable and one tool resource. Both teams may carry 5 pieces of the consumable and 1 piece of the tool resource with themselves, the costs of usage are 15 EUR and 100 EUR per piece, respectively. Each task requires 1 piece of consumable and 1 piece of tool present. Note that this basically means that tool requirements are trivially satisfied if a team carries a single piece, nevertheless, its cost must be paid. In general, there could be upper limits on resource availability and unique requirements for each task and each team.

The last part of the problem formulation is the relations between tasks. These can be described by ordered pairs of tasks as listed below, also depicted in Fig. 11.

• Tasks K_1a, K_1b, K_1c1, K_1c2, K_1d describe a single complex procedure which is divided into simple tasks. These must be carried out in the following order: first K_1a, then K_1b, then K_1c1 and K_1c2 in parallel by two teams, and finally K_1d. Leaving the site before completing the procedure would be hazardous – therefore, either a team shall be present to guard the site while a next team arrives, or the site must be secured by a closing activity, and then an opening activity must be performed by the next team. Therefore, the following five protected precedence relations are included in the problem formulation: (K_1a, K_1b), (K_1b, K_1c1), (K_1b, K_1c2), (K_1c1, K_1d), (K_1c2, K_1d). There is also a parallel execution relation, for (K_1c1, K_1c2).

• If, at any point, a protected precedence relation is chosen to be satisfied by securing the site, a cost of 30 EUR is incurred and the closing and opening activities take 15 min each.

• Tasks K_3a and K_3b represent two pieces of the same procedure, they must be done in the given order, and by the same team, as information from completing K_3a is required for K_3b and communication between teams is problematic. Therefore, a same-team precedence relation is included for (K_3a, K_3b).

• Tasks K_1a involves operating a sensitive part of the electric system which would interfere with K₂ and K_3a. Therefore, two mutual exclusion relations are also included: (K_1a, K₂), (K_1a, K_3a). These relations prevent execution times from overlapping. Note that K₂ and K_3a are not related and may overlap.

Fig. 11

Pairwise task relations in the motivational example

5.2 Solution of the motivational problem

The data file describing the motivational problem was implemented in GNU MathProg, and was solved to optimality with the GLPSOL solver.

In the optimal solution, all the required relation constraints are met: K_3a and K_3b are executed by the same team (Team₁), K_1c1 and K_1c2 are executed in parallel, K_1a is solved in an interval disjoint to both K_3a and K₂, and the site S₁ is never left unsecured between executing tasks there. In fact, teams always choose to wait in case of a protected precedence relation and no closing and opening activities are ever performed. Also, K_1b is fit in its expected time window, therefore no penalties arise. See Table 1 for the detailed timetable of the teams.

Table 1 Schedules according to the optimal solution of the motivational example

The objective is 1944 EUR, this is the minimal cost for which all tasks can be executed in this workday. This is achieved by Team₁ visiting all three sites. Meanwhile Team₂ only does some specific tasks at S₁ which are the first part of the consecutive tasks there, before both teams start executing K_1c1 and K_1c2 simultaneously. It seems that Team₁ executes as many tasks as possible. The faster but more expensive Team₂ is only used to reduce the load on Team₁, and to help with the two parallel tasks which need cooperation. Note that Team₂ would do the parallel task K_1c2 in 30 min, but their execution time is prolonged by 15 min, because Team₁ requires 45 min for K_1c1. Additional waiting and idle times are not needed, as every constraint is already satisfied and teams’ working cost of 60 EUR/hour is incurred even if the teams are idle.

This optimal solution was actually generated by the Standalone MILP model formulation. As the example is small, the Standalone MILP was sufficient without any algorithmic framework to provide this globally optimal solution for the motivational problem.

5.3 Overview of standalone tests

Three series of tests were performed, each focusing on the impact of a specific component of the MILP model on its overall performance.

• The first series focuses on the effect of task site count.

• The second series focuses on pairwise relationships between tasks.

• The third series focuses on the parameter ${N}_{m}$ which determines available job slots.

In each of the three series, a set of mobile workforce management problem instances were constructed. The basis of these test sets is a “main problem instance”. This main problem instance consists of 18 tasks to be solved on 4 different sites by 3 working teams. Each team has its own constant travelling and task execution costs and times, and six predefined job slots $(\forall m: {N}_{m}=6$). Tasks were subject to absolute and expected time windows, which slightly reduce the possible execution from the 08:00 in the morning to 16:00 in the afternoon interval for all tasks. The first five tasks mutually exclude each other, the other tasks involve all other kinds of relations mentioned. The problem contains a single consumable and a tool resource. Full details of the problem can be found in the supplementary material.

To obtain the test set for each series, minor modifications were made to the main problem instance, according to the currently investigated model component, resulting in several, slightly different problem instances.

Solutions for all instances were found by the Gurobi MILP solver, version 8.1, on a workstation with Ubuntu 18.04.1 LTS, Intel i7-4770 3.40 GHz CPU and 16 GB RAM. The time limit was one hour per test case.

Our main interests were the time required by the solver to finish an instance, and the optimal objective it reported (total costs, displayed in EUR). In the tables presented, the number of constraints (rows) and variables (columns) are also shown for each test case, as well as the number of integer (binary) variables. Note that these data shall be interpreted with caution when concluding model complexity, as many of the rows and columns could be eliminated even in the preprocessing steps of modern MILP solvers, also, there are many strong knapsack constraints for the binaries as well.

5.4 Task site count

In the first series, the sites of the tasks were in focus. A set of 9 problem instances was constructed based on the following guidelines.

• All data are equivalent to the main problem instance except for the number of task sites and their distribution among tasks.

• 3, 4, and 5 different task sites were considered. Note that the main problem instance features 4 sites.

• For each site count, three different variations are constructed. The variations differ only in the site distribution of tasks, but in all cases, the occurrence of all available sites is well-balanced (the difference is at most 1).

One of the instances is the main problem instance itself. Note that although the number of different task sites is not the same, these were included in the problem data, just not always used.

Results reported by the MILP solver for these 9 test cases can be observed in Table 2.

Table 2 Impact of task sites on solver performance

It can be observed that the number of sites has a very large impact on the problem complexity. Comparing the main problem instance to its two variations required significantly more time to be solved, where the objective only changed a little or not at all.

Two test cases with 5 sites could not be completed in time limit.

One important property of the model is that the number of sites can be a bottleneck, as the more sites are there, the more are the variables and constraints required by constraints for travelling. It is reflected from the results that as the number of sites increases, so does the time required for solving the model, while the objective only changes a little. A problem with different sites for all tasks should contain considerably fewer tasks to be able to be solved with this form of the model in a short time. Likewise, even fewer sites might lead to faster solutions.

Note that the distribution of sites among tasks, although seem to greatly affect solver performance, does not affect the number of rows, columns or binaries. The equal number of rows (that means, constraints) is due to the fact that all task sites were included in the model each time, but only a smaller subset was used in the different instances. The results indicate that the Standalone MILP model is only effective in those mobile workforce scenarios where the number of sites is small.

5.5 Task relations

The usage of relations between tasks can make problems harder or easier. Relations actually constrain the search space, thus making the problem effectively smaller. On the other hand, some additional variables, even binaries are introduced, which can make the model more complex.

Two of the supported pairwise relations are selected to be tested thoroughly: free precedence and mutual exclusions. The free precedence is interesting because it only imposes a constraint, meanwhile the mutual exclusion introduces a binary decision variable.

The test set was constructed as follows.

• From the main problem instance, exactly 1, 2, and 3 of the existing free precedence relations are excluded to obtain 3 additional instances.

• From the main problem instance, 1–10 of the already existing mutual exclusion relations were excluded one by one to obtain 10 additional instances.

Results for the 14 test cases obtained this way are shown in Table 3.

Table 3 Impact of pairwise task relations on solver performance

The objective was not affected in this scenario, only the runtimes varied between 2 and 7 min.

Excluding free precedence relations, each of which imposes a single constraint, might lead to more or less difficult models, but not changes in magnitude. An interesting outcome is a gradual decrease in solver runtime as there were less precedence relationships, as the opposite could be expected because of the increasing search space. This property of MILP models is very hard to foresee: sometimes constraints that decrease the number of cases to be checked makes the model a bit more difficult in practice. This depends on the solver as well.

With the exclusion of mutual exclusion relations, however, the time needed for the solver to prove optimality greatly varies, as for a mutual exclusion, not only two constraints, but an additional binary variable is also introduced. But again, there is no difference in magnitude. It is therefore not possible to tell a rule of thumb on how a mutual exclusion affects the complexity of a specific problem.

5.6 Task and job slot count

One main drawback of the Standalone MILP model is the requirement of the ${N}_{m}$ parameters to be provided beforehand. These determine the available job slots for each team, and has a great impact on the number of binary variables, hence we expect a great impact on the computational performance as well. A too small ${N}_{m}$ may exclude valuable optimal solutions, while a too large ${N}_{m}$ may result in a model which is computationally too complex.

In this series, the test cases were constructed in the following way.

• The motivational problem is included in this test set to illustrate problem sizes. Recall that the motivational problem includes two teams and 8 tasks, with ${N}_{m}=8$ for both teams.

• The main problem instance is itself included, and is the basis for further instances. Recall that the main problem instance consists of 3 teams and 18 tasks, with ${N}_{m}=6$ for all three teams.

• 1–3 tasks were excluded from the original problem, together with their relation constraints to obtain 3 additional problem instances.

• From the instance where 3 tasks were already excluded, 1–3 additional job slots were removed from each team one by one, resulting in 3 additional instances. Therefore, the problem instance obtained in the end had only 15 tasks and ${N}_{m}=5$ for all three teams, which is just enough to schedule all tasks.

• Finally, based on the main problem instance again, 1–3 new job slots were added to the teams one by one, resulting in 3 further problem instances. Therefore, the last instance in this direction had ${N}_{m}=7$ for all three teams.

Results for these 11 instances in total can be seen in Table 4.

Table 4 Effects of task and job slot count on solver performance

If tasks are excluded from the model, the complexity clearly and rapidly drops. When the resulting free job slots are also eliminated one by one, the objective increases, which means that some optimal solutions become infeasible, as expected. This phenomenon indicates that the eliminated job slot was used in the previous optimal solution.

On the other hand, when job slots are added, the objective does not increase after the second one, but the solver still needs more time to find the optimum. In any case, the more job slots are there, the more complex the model is, possibly having better solutions as well.

6 Case study for the algorithmic framework

To demonstrate the usage of the MILP model with the algorithmic framework, a different group of test instances is presented here. These instances are randomly generated problems with 6 task sites, 3 teams, each at different depots, and task count is gradually increased. Again, the full test results, problem generation, MILP model and algorithm codes are available as “MWM model and case studies”, see Eles et al. (2020), in an executable format.

It shall be noted that task data were the same through all cases with the exception of task count and job slot count variation. To run the Standalone MILP, the number of predefined job slots, ${N}_{m}$ must be set. In this case study, the formula of Eq. (65) is used. This is sufficient to schedule all tasks for any task count $\left|K\right|$ and team count $\left|M\right|$, although does not allow any single team to execute too many tasks.

$$N_{m} = \frac{\left| K \right|}{{\left| M \right|}} \cdot 1.2 + 1 \forall m \in M$$

(65)

Note that this series of tests lacks pairwise relations.

The test series was conducted in the following manner. Starting from 5, the task count was gradually increased, and for each task count a random problem instance was generated, and solved by the two methods.

6.1 Comparison of the two methods

The Standalone MILP model and the algorithmic framework was executed on test cases randomly generated for 5–15 tasks. Found objective values and solver runtimes are shown in Table 5.

Table 5 Comparison of the Standalone MILP solution and the algorithmic framework

It can be seen that the Standalone MILP model solution procedure exceeds the one-hour time limit early, at 11 tasks, due to the higher number of sites in this problem series. Meanwhile the algorithmic framework succeeds in 2.69 s for 15 tasks. We can see that the difference between the two methods in terms of objective is no more than 5.68% when both methods finish in an hour, and it is no more than 6.74% when considering the other instances when the standalone MILP model timed out. In the latter cases, we can give a rough estimate between the optimal solution of the MILP and the solution the algorithm presented, and it obtains its maximum at 31.05% for 15 tasks. There was even a case, for 7 tasks, where the algorithm found the optimal solution of the MILP model.

6.2 Larger instances

To test the algorithmic framework, task count was further increased by 5 each time, from 20 to 130. Again, for each particular task count, a problem instance was generated, but this time only solved by the algorithmic framework. See Table 6 for the problem size, solver runtime and achieved objective for each problem instance. For 130 tasks the algorithm did not finish in 1 h so larger instances were not generated.

Table 6 Results of the algorithmic framework for 20–130 tasks

It can be observed that the overall size of the problem increases rapidly, while the objective and the time needed by the algorithm increases gradually. Recall that the MILP model used by the framework has a relatively small search space, as most of the integer variables are set a priori. This is why the algorithm is much faster than the Standalone MILP model.

One interesting result in this series is that the algorithm failed to finish for the test case of 80 tasks (marked by asterisks). This can happen as a consequence of the heuristic nature: the only feasible solutions may be excluded by early decisions. The last task could not be inserted to the schedule because of the previous ordering, so finally only 79 tasks were scheduled. This situation is more likely when narrow absolute time windows or relations between tasks are given. For these cases, more sophisticated algorithms will be needed in the future which are capable, for example, of looking ahead during the search to accommodate pairwise relations between tasks as well.

7 Conclusions

A novel MILP model was developed for the mobile workforce management problem. The problem can be regarded as a generalization of well-known problems like vehicle routing, scheduling and resource allocation. The problem definition is stated in detail with the help of an illustrative example and its optimal solution. The MILP model is unique in two different ways. First, a wide range of features is supported as problem data that can be set, which has not yet been done before. Second, the logic of decision variables of the MILP falls into the slot-based category which was developed for scheduling problems, but not thoroughly investigated for the case of VRP or mobile workforce management.

The model introduces a set of job slots for each team, separated by travelling slots representing possible movement between sites. The execution and travelling times, and potential limits can be different for each team. Tasks can also be subject to absolute or expected time windows. Packing and unpacking times can be taken into account, based on whether the team does consecutive tasks at the same site or not. Consumable and tool resources are also considered. Pairwise task relations like mutual exclusion, precedence of tasks, parallel execution are supported. The MILP model is described in detail in this work and was implemented in GNU MathProg modelling language.

To make it able to solve larger problems, an algorithmic framework is also presented, with which heuristic solutions can be found in acceptable time. The algorithm uses a greedy heuristic. At a single time, one new task is chosen and inserted into the already existing schedule, using an extension of the original MILP model and optimizing for its objective.

One test problem and its scaled versions were solved in a case study by a commercial MILP solver, Gurobi. Most variants of this problem with 18 tasks, 4 sites and 3 teams were solved in an hour to optimality. The impact of the number of sites, tasks, job slots and pairwise relations were investigated for the Standalone MILP model. Results suggest that the model works best for a low number of task sites. Care must be taken to adjust the number of job slots to the number of tasks, as the former severely affects performance but not always the optimal solution.

The case study also involved the algorithmic framework, with which we can get heuristic solutions for problems with 20–125 tasks in an hour. Although optimality is not guaranteed and sometimes not all tasks could be scheduled, the framework was capable to report solutions for much larger problem instances than what the MILP model could handle.

The wide range of features the model supports to be taken into account makes it a candidate for more elaborate heuristic algorithms to be developed and implemented in the future. The algorithm can be improved to better adapt to time windows, resource utilization, and most importantly, pairwise relations between tasks. Extension of the search space of the MILP model during an algorithmic step is a promising direction. This may involve scheduling multiple new tasks at the same time, exchanging or dropping present tasks, or other manipulations of the existing schedule.

Nomenclature

Note that some of the sets, parameters and variables are only used in the algorithmic framework for the MILP model. This is explicitly mentioned in the nomenclature for those elements.

1.1 Sets

Sets are described here with typical index symbols for their elements.

$k\in K$ :

Set of tasks

$k\in {K}^{done}$ :

Set of tasks already scheduled (algorithm only)

${K}^{done}\subseteq K$ $k\in {K}^{rem}$ :

Set of tasks not scheduled yet (algorithm only)

${K}^{rem}=K\setminus {K}^{done}$ $m\in M$ :

Set of teams

$\left(m,i\right)\in {J}_{slots}$ :

Set of job slots

$i\in \left[1,{N}_{m}\right]$ $\left(m,i\right)\in {T}_{slots}$ :

Set of travelling slots

$i\in \left[0,{N}_{m}\right]$ $\left(m,i\right)\in {S}_{points}$ :

Set of site time points of interest (or site slots)

$i\in \left[0,{N}_{m}+1\right]$ $\left({k}_{1}{,k}_{2}\right)\in {P}^{free}$ :

Set of free precedence relationships

${k}_{1},{k}_{2}\in K$ $\left({k}_{1}{,k}_{2}\right)\in {P}^{prot}$ :

Set of protected precedence relationships

${k}_{1},{k}_{2}\in K$ $\left({k}_{1}{,k}_{2}\right)\in {P}^{same}$ :

Set of same-team precedence relationships

${k}_{1},{k}_{2}\in K$ $\left({k}_{1}{,k}_{2}\right)\in {P}^{prec}$ :

Set of all precedence relations. ${P}^{prec}={P}^{free}\cup {P}^{prot}\cup {P}^{same}$

$\left({k}_{1}{,k}_{2}\right)\in {P}^{mutex}$ :

Set of mutual exclusion relationships. ${k}_{1},{k}_{2}\in K$

$\left({k}_{1}{,k}_{2}\right)\in {P}^{parallel}$ :

Set of parallel execution relationships. ${k}_{1},{k}_{2}\in K$

$r\in {R}^{cons}$ :

Set of consumable resources

$r\in {R}^{tool}$ :

Set of tool resources

$r\in R$ :

Set of all resources. $R={R}^{cons}\cup {R}^{tool}$

$s\in {S}_{depot}$ :

Set of depot sites

$s\in {S}_{tasksites}$ :

Set of task execution sites. ${S}_{tasksites}\cap {S}_{depot}=\varnothing$

$s\in S$ :

Set of all sites. $S={S}_{tasksites}\cup {S}_{depot}$

1.2 Parameters

All numeric parameters are assumed to be nonnegative numbers.

${C}_{m}^{unpack}: m\in M$ :

Unpacking cost of team $m$ at arrival on a site

${C}_{m}^{pack}: m\in M$ :

Packing cost of team $m$ before departure from a site

${C}_{k,m}^{exec}: k\in K, m\in M$ :

Cost of task $k$ if executed by team $m$

${C}_{m}^{travel}: m\in M$ :

Cost factor for travelling time of team $m$

${C}_{m}^{work}: m\in M$ :

Cost factor for total working time of team $m$

${C}_{k}^{earliness}: k\in K$ :

Penalty cost factor if task $k$ if executed earlier than ${T}_{k}^{expected,start}$

${C}_{k}^{lateness}: k\in K$ :

Penalty cost factor if task $k$ if finished later than ${T}_{k}^{expected,end}$

${C}_{r}^{res}: r\in R$ :

Cost of utilization of one unit of resource $r$

${D}_{{s}_{1},{s}_{2}}: {s}_{1},{s}_{2}\in S$ :

Travelling distance between sites ${s}_{1}$ and ${s}_{2}$

${D}_{m}^{travel,MAX}: m\in M$ :

Maximum total distance team $m$ may travel

${H}_{k}^{slot}: k\in {K}^{done}$ :

Job slot task $k$ was scheduled at (algorithm only). ${H}_{k}^{slot}\in {J}^{slots}$

${N}_{m}: m\in M$ :

Number of predefined job slots for team $m$

${Q}_{r}^{CAP}: r\in R$ :

Total available amount of resource $r$

${Q}_{r,k,m}^{req}: r\in R, k\in K, m\in M$ :

Requirement of resource $r$ for execution of $k$ by team $m$

${Q}_{r,m}^{MAX}: r\in R, m\in M$ :

Maximal amount of resource $r$ that team $m$ may carry

${S}_{m}^{start}: k\in K$ :

Starting position of team $m$. ${S}_{m}^{start}\in {S}_{depot}$

${S}_{m}^{end}: k\in K$ :

Final position of team $m$. ${S}_{m}^{start}={S}_{m}^{end}$ is assumed for simplicity

${S}_{k}^{task}: k\in K$ :

Site of task $k$

${T}_{k}^{close}: k\in K$ :

Site closing time after task $k$ in a protected precedence relation

${T}_{k}^{open}: k\in K$ :

Site opening time before task $k$ in a protected precedence relation

${T}_{m}^{pack}: m\in M$ :

Packing time of team $m$, before departure from a site

${T}_{m}^{unpack}: m\in M$ :

Unpacking time of team $m$, after arrival on a site

${T}_{k,m}^{exec}: k\in K$ :

Net time spent on execution of task $k$ if done by team $m$

${T}_{k}^{earliest}: k\in K$ :

Start of absolute time window of task $k$

${T}_{k}^{latest}: k\in K$ :

End of absolute time window of task $k$

${T}_{k}^{expected,start}: k\in K$ :

Start of expected time window of task $k$

${T}_{k}^{expected,end}: k\in K$ :

End of expected time window of task $k$

${T}_{m}^{travel,MAX}: m\in M$ :

Total time that team $m$ may spend travelling, (un)packing and idle

${T}_{m}^{work,MAX}: m\in M$ :

Total time that team $m$ may be in duty during the day

${T}^{DAY,start}$ :

Starting time of the workday

${T}^{DAY,end}$ :

Ending time of the workday

${T}^{WORKDAY}$ :

Length of the whole workday. ${T}^{WORKDAY}= {T}^{DAY,end}- {T}^{DAY,start}$

${V}_{m}:m\in M$ :

Speed of team $m$ on the map. ${V}_{m}>0$

1.3 Binary decision variables

In general, 1 means that the logical statement described by the variable is true, otherwise the value is zero. Note that only ${a}_{k,m,i}$, ${p}_{{k}_{1},{k}_{2}}^{prot}$, ${p}_{{k}_{1},{k}_{2}}^{mutex}$ from the original formulation, and ${x}_{k}^{task}$, ${x}_{m}^{team}$ ${x}_{m,i}^{slot}$ used in the algorithmic framework are mandatorily binary. All other binaries mentioned here are unambiguously derived from the former six, and hence are treated as continuous $\left[\mathrm{0,1}\right]$ variables in the model implementation.

${a}_{k,m,i}: k\in K,\left(m,i\right)\in {J}^{slots}$:

Task $k$ is executed by team $m$ in the $i$ ^th job slot $(m,i)$

${a}_{k,m}^{task}: k\in K, m\in M$:

Task $k$ is assigned to team $m$ to be executed

${b}_{m,i,s}^{present}: \left(m,i\right)\in {S}^{slots}, s\in S$:

Team $m$ is at site $s$ at site slot $(m,i)$

${b}_{m,i,{s}_{1},{s}_{2}}^{sch}:\left(m,i\right)\in {T}^{slots}, {s}_{1},{s}_{2}\in S$:

Team $m$ moves from ${s}_{1}$ to ${s}_{2}$ in travelling slot $(m,i)$. ${s}_{1}\ne {s}_{2}$

${b}_{m,i}^{travel,move}: \left(m,i\right)\in {T}^{slots}$:

Team $m$ changes site in travelling slot $(m,i)$

${p}_{k}^{open}: k\in K$:

Site ${S}_{k}^{task}$ of task $k$ must be opened before executing task $k$

${p}_{k}^{close}: k\in K$:

Site ${S}_{k}^{task}$ of task $k$ must be closed before executing task $k$

${p}_{{k}_{1},{k}_{2}}^{prot}: ({k}_{1},{k}_{2})\in {P}^{prot}$:

Task sites between ${k}_{1}$ and ${k}_{2}$ are closed and opened

${p}_{{k}_{1},{k}_{2}}^{mutex}: ({k}_{1},{k}_{2})\in {P}^{mutex}$:

Task ${k}_{1}$ is executed before task ${k}_{2}$ to respect mutual exclusion

${x}_{k}^{task}: k\in {K}^{rem}$:

Task $k$ is selected to be the new task (algorithm only)

${x}_{m}^{team}: m\in M$:

Team $m$ is selected to do the new task (algorithm only)

${x}_{m,i}^{slot}: \left(m,i\right)\in {J}^{slots}$:

The new task goes to job slot $\left(m,i\right)$ of team $m$ (algorithm only)

${y}_{m,i}: \left(m,i\right)\in {T}^{slots}$:

The new task goes before travelling slot $\left(m,i\right)$ (algorithm only)

1.4 Continuous variables

By default, all variables have a lower bound of zero and no upper bound, except those referring to points in time, which must fit in the interval $\left[{T}^{DAY,start},{T}^{DAY,end}\right]$.

${c}_{k}^{pen,early}: k\in K$:

Penalty for starting task $k$ earlier than its expected window

${c}_{k}^{pen,late}: k\in K$:

Penalty for finishing task $k$ later than its expected window

${c}^{travel}$:

Total cost of travelling

${c}^{packing}$:

Total cost of packing and unpacking at sites

${c}^{tw}$:

Total cost of penalties related to time windows

${c}^{exec}$:

Total cost of executions of tasks

${c}^{res}$:

Total cost of resource utilization

${c}^{opcl}$:

Total cost of opening/closing in protected precedence relations

${c}^{work}$:

Total cost of team working times

${c}^{total}$:

Sum of costs from all sources

${q}_{r,m,i}^{req}: r\in R, \left(m,i\right)\in {J}^{slots}$:

Amount of resource $r$ used in job slot$(m,i)$

${q}_{r,m}^{carry}: r\in R, m\in M$:

Amount of resource $r$ carried by team $m$ from the starting depot

${t}_{k}^{start}: k\in K$:

Starting time of the execution of task$k$

${t}_{k}^{end}: k\in K$:

Ending time of the execution of task$k$

${t}_{k}^{open}: k\in K$:

Opening time at the site ${S}_{k}$ of task $k$ before its execution.

${t}_{k}^{close}: k\in K$:

Closing time at site ${S}_{k}$ of task $k$ after its execution

${t}_{m,i}^{idle}: \left(m,i\right)\in {T}^{slots}$:

Idle time in travelling slot$\left(m,i\right)$

${t}_{k}^{presence,start}: k\in K$:

Start of job slot in which task $k$ is executed

${t}_{k}^{presence,end}: k\in K$:

End of job slot in which task $k$ is executed

${t}_{k}^{slack}: k\in K$:

Delay in net execution for a task$k$

${t}_{m,i}^{travel,start}: \left(m,i\right)\in {T}^{slots}$:

Starting time of travelling slot$(m,i)$

${t}_{m,i}^{travel,end}: \left(m,i\right)\in {T}^{slots}$:

Ending time of travelling slot$(m,i)$

${t}_{k}^{wait,before}: k\in K$:

Waiting time spent by the team before executing task$k$

${t}_{k}^{wait,after}: k\in K$:

Waiting time spent by the team after executing task$k$