Structural fluctuations in ensembles of nanoparticles

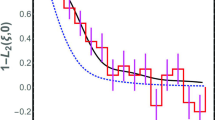
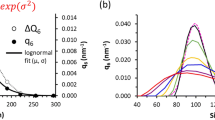
Abstract

Caused by the interaction between the particles, structural fluctuations influence thermodynamics and order of transformation of an ensemble of nanoparticles. A stringed thermodynamic analysis revealed that, in fluctuating ensembles, the ratio of particle numbers in the equilibrium over the one in the non-equilibrium phase is independent of any metastable in between. Structural transformations in such ensembles, connected to latent heat, are of infinite order. These findings are summarized in a set of theorems ruling structural fluctuations. Finally, the consequences of fluctuations are demonstrated by an example.

Appendix

Derivatives of the free enthalpy with respect to temperature

We consider derivatives of a class of functions f _i (c _i ,c ₂) with respect to δ and calculate their derivatives $\partial ^p {{f_i } \mathord{\left/ {\vphantom {{f_i } {\partial \delta }}} \right. \kern-\nulldelimiterspace} {\partial \delta }}^p$ for 0 < p and $\delta \Rightarrow 0$. The first function to be investigated is

$$ f_1 = - \left( {c_1 s_1 + c_2 s_2 } \right)\delta $$

(A1)

with

$$ c_1 = \left( {1 + e^\varphi } \right)^{ - 1} \;,\;\varphi = \left( {s_1 - s_2 } \right){\delta \mathord{\left/ {\vphantom {\delta {\left( {R\left( {T_c + \delta } \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {R\left( {T_c + \delta } \right)} \right)}}. $$

(A2)

The quantities T _c corresponds to T _cross and R to kM/m in the main body of this paper. Note that the fractions c ₁, c ₂ are related by $c_2 = 1 - c_1$, and c ₁, c ₂ are 1/2 for δ = 0. The first derivative follows as $\left. {{{\partial f_1 } \mathord{\left/ {\vphantom {{\partial f_1 } {\partial \delta }}} \right. \kern-\nulldelimiterspace} {\partial \delta }}} \right|_{\delta = 0} = {{ - \left( {s_1 + s_2 } \right)} \mathord{\left/ {\vphantom {{ - \left( {s_1 + s_2 } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$ and is symmetric with respect to s ₁ and s ₂.

The Leibniz rule allows immediately to write with $\delta \Rightarrow 0$

$$ \partial ^p \left. {{{f_1 } \mathord{\left/ {\vphantom {{f_1 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }}} \right|_{\delta = 0} = p\left( {s_2 - s_1 } \right) \cdot \partial ^{p - 1} {{c_1 } \mathord{\left/ {\vphantom {{c_1 } {\partial \delta ^{p - 1} }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^{p - 1} }},\quad p \ge 2. $$

(A3)

Therefore, the problem is reduced to the derivatives of c ₁ with respect to δ. Since c ₁ can be formulated as a function $c_1 \left( {\phi \left( \delta \right)} \right)$, see (A2), the chain rule makes it necessary to have the derivatives

$$ \begin{aligned} \left. {\partial ^n {{c_1 } \mathord{\left/ {\vphantom {{c_1 } {\partial \phi ^n }}} \right. \kern-\nulldelimiterspace} {\partial \phi ^n }}} \right|_{\delta = 0} = :\,&A_n \cdot {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}^n ,\quad n < 1,{\text{ uneven,}} \hfill \\ &{\text{ 0 }}\quad\qquad, \quad n < 1,{\text{ even;}} \hfill \\ \end{aligned} $$

(A4)

$$ \left. {{{\partial ^n \varphi } \mathord{\left/ {\vphantom {{\partial ^n \varphi } {\partial \delta ^n }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^n }}} \right|_{\delta = 0} = - n!{{\left( {s_2 - s_1 } \right)} \mathord{\left/ {\vphantom {{\left( {s_2 - s_1 } \right)} {\left( {RT_c^n } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {RT_c^n } \right)}}. $$

(A5)

The quantities A _n are premultipliers independent of s ₁ and s ₂.

Calculating ${{\partial ^p c_1 } \mathord{\left/ {\vphantom {{\partial ^p c_1 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }}$ yields p terms. Each term is the product of the nth derivative (A4), n = 1,…p, with an expression being the product of two derivatives (A5), so that this expression is always proportional to (s ₂ − s ₁)ⁿ. Since only the uneven terms (n=1, 3,…) survive due to (A4), we find that according to (A3), the pth derivative ${{\partial ^p f_1 } \mathord{\left/ {\vphantom {{\partial ^p f_1 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }}$ is a series of $\left( {\left[ {{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-\nulldelimiterspace} 2}} \right] + 1} \right)$ terms of even powers of (s ₂ − s ₁). This means finally that the pth derivative of f ₁ is symmetric with respect to s ₁ and s ₂. In order to verify successfully verify such an expression, the symbolic processor MAPLE (www.maple.com) has been employed.The next function to be investigated is

$$ f_2 = c_1 \ell n\;c_1. $$

(A6)

The first derivative is

$$ \left. {{{\partial f_2 } \mathord{\left/ {\vphantom {{\partial f_2 } {\partial \delta }}} \right. \kern-\nulldelimiterspace} {\partial \delta }}} \right|_{\delta = 0} = \left( {\left. {{{\partial c_1 } \mathord{\left/ {\vphantom {{\partial c_1 } {\partial \delta }}} \right. \kern-\nulldelimiterspace} {\partial \delta }}} \right|_{\delta = 0} } \right)\left( {1 - \ell n2} \right) = \left( {s_2 - s_1 } \right){{\left( {1 - \ell n2} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \ell n2} \right)} {4RT_c }}} \right. \kern-\nulldelimiterspace} {4RT_c }} $$

and antimetric in s ₁ and s ₂. According to the Leibniz rule ${{\partial ^p f_2 } \mathord{\left/ {\vphantom {{\partial ^p f_2 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }},p > 1$, consists of (p + 1) terms being products of ${{\partial ^{p - \ell } c{}_1} \mathord{\left/ {\vphantom {{\partial ^{p - \ell } c{}_1} {\partial \delta ^{p - \ell } }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^{p - \ell } }}$ and the $\ell - th$ derivative of $\ell nc_1$. As we have shown above for f ₁, the first multiplier is always an uneven function in powers of (s ₂ − s ₁) for $p - \ell \ge 2$, and therefore, is asymmetric in s ₁ and s ₂. The second multiplier is a sum of $\ell$ terms, which can be even or uneven in powers of (s ₂ − s ₁). Finally, a series of even or uneven powers of (s ₂ − s ₁) remains for ${{\partial ^p f_2 } \mathord{\left/ {\vphantom {{\partial ^p f_2 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }}$ at δ = 0.

As last case, we consider

$$ f_3 = c_2 \ell nc_2\,\,{\text{with}}\,\,c_2 = 1 - c_1. $$

(A7)

In analogy of the treatment of f ₂, the even powers of (s ₂ − s ₁) in ${{\partial ^p f_3 } \mathord{\left/ {\vphantom {{\partial ^p f_3 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }},p > 1$, have the same sign as in ${{\partial ^p f_2 } \mathord{\left/ {\vphantom {{\partial ^p f_2 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }},\delta = 0,p > 1$ and for δ=0 also the same coefficients, since $c_1 = c_2 = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$. However, the first multipliers ${{\partial ^{p - \ell } c_2 } \mathord{\left/ {\vphantom {{\partial ^{p - \ell } c_2 } {\partial \delta ^{p - \ell } }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^{p - \ell } }}$ are always uneven and are ${{ - \partial ^{p - \ell } c_1 } \mathord{\left/ {\vphantom {{ - \partial ^{p - \ell } c_1 } {\partial \delta ^{p - \ell } }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^{p - \ell } }}$. This means that the uneven powers of (s ₂ − s ₁) in ${{\partial ^p f_3 } \mathord{\left/ {\vphantom {{\partial ^p f_3 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }},\delta = 0$, have coefficients with the same value as in ${{\partial ^p f_2 } \mathord{\left/ {\vphantom {{\partial ^p f_2 } {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }}$, δ = 0, however, with a negative sign.

The conclusion is that $\partial ^p {{\left( {f_2 + f_3 } \right)} \mathord{\left/ {\vphantom {{\left( {f_2 + f_3 } \right)} {\partial \delta ^p }}} \right. \kern-\nulldelimiterspace} {\partial \delta ^p }} = 0$, δ = 0, only have even powers of (s ₂ − s ₁). This has also been verified by using MAPLE (http://www.maple.com) up to a high order of the derivative.