Skip to main content
SpringerLink
Log in

Nonlocal elasticity: an approach based on fractional calculus

  • Multi-Scale and Multi-Physics Modelling for Complex Materials
  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

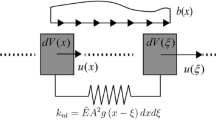
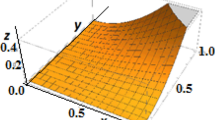
Fractional calculus is the mathematical subject dealing with integrals and derivatives of non-integer order. Although its age approaches that of classical calculus, its applications in mechanics are relatively recent and mainly related to fractional damping. Investigations using fractional spatial derivatives are even newer. In the present paper spatial fractional calculus is exploited to investigate a material whose nonlocal stress is defined as the fractional integral of the strain field. The developed fractional nonlocal elastic model is compared with standard integral nonlocal elasticity, which dates back to Eringen’s works. Analogies and differences are highlighted. The long tails of the power law kernel of fractional integrals make the mechanical behaviour of fractional nonlocal elastic materials peculiar. Peculiar are also the power law size effects yielded by the anomalous physical dimension of fractional operators. Furthermore we prove that the fractional nonlocal elastic medium can be seen as the continuum limit of a lattice model whose points are connected by three levels of springs with stiffness decaying with the power law of the distance between the connected points. Interestingly, interactions between bulk and surface material points are taken distinctly into account by the fractional model. Finally, the fractional differential equation in terms of the displacement function along with the proper static and kinematic boundary conditions are derived and solved implementing a suitable numerical algorithm. Applications to some example problems conclude the paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Mainardi F (2010) Fractional calculus and waves in linear viscoelasticity: an introduction to mathematical models. Imperial College Press, London

    Book  Google Scholar 

  2. Rossikhin YA, Shitikova MV (2010) Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl Mech Rev 63(010801):1–52

    Google Scholar 

  3. Mainardi F, Luchko Y, Pagnini G (2001) The fundamental solution of the space-time fractional diffusion equation. Fract Calc Appl Anal 4:153–192

    MathSciNet  MATH  Google Scholar 

  4. Metzler R, Nonnenmacher TF (2002) Space- and time-fractional diffusion and wave equations, fractional Fokker–Planck equations, and physical motivation. Chem Phys 284:67–90

    Article  ADS  Google Scholar 

  5. Zoia A, Rosso A, Kardar M (2007) Fractional laplacian in bounded domains. Phys Rev E 76(021116):1–11

    MathSciNet  Google Scholar 

  6. Magin RL, Abdullah O, Baleanu D, Zhou XJ (2008) Anomalous diffusion expressed through fractional order differential operators in the Bloch–Torrey equation. J Magn Reson 190:255–270

    Article  ADS  Google Scholar 

  7. Macdonald JR, Evangelista LR, Lenzi EK, Barbero G (2011) Comparison of impedance spectroscopy expressions and responses of alternate anomalous Poisson–Nernst–Planck diffusion equations for finite-length situations. J Phys Chem C 115:7648–7655

    Article  Google Scholar 

  8. Carpinteri A, Cornetti P (2002) A fractional calculus approach to the description of stress and strain localization in fractal media. Chaos, Solitons Fractals 13:85–94

    Article  MATH  ADS  Google Scholar 

  9. Carpinteri A, Chiaia B, Cornetti P (2001) Static-kinematic duality and the principle of virtual work in the mechanics of fractal media. Comput Meth Appl Mech Eng 191:3–19

    Article  MATH  Google Scholar 

  10. Tarasov VE (2005) Continuous medium model for fractal media. Phys Lett A 336:167–174

    Article  MATH  ADS  Google Scholar 

  11. Michelitsch TM, Maugin GA, Rahman M, Derogar S, Nowakowski AF, Nicolleau FCGA (2012) An approach to generalized one-dimensional self-similar elasticity. Int J Eng Sci 61:103–111

    Article  MathSciNet  Google Scholar 

  12. Carpinteri A, Cornetti P, Sapora A (2009) Static-kinematic fractional operators for fractal and non-local solids. ZAMM-Z Angew Math Mech 89:207–217

    Article  MathSciNet  MATH  Google Scholar 

  13. Lazopoulos KA (2006) Non-local continuum mechanics and fractional calculus. Mech Res Commun 33:753–757

    Article  MathSciNet  MATH  Google Scholar 

  14. Di Paola M, Zingales M (2008) Long-range cohesive interactions of nonlocal continuum mechanics faced by fractional calculus. Int J Solids Struct 45:5642–5659

    Article  MATH  Google Scholar 

  15. Carpinteri A, Cornetti P, Sapora A, Di Paola M, Zingales M (2009) An explicit mechanical interpretation of Eringen non-local elasticity by means of fractional calculus. In: Proceedings of 19th Italian Conference on Theoretical and Applied Mechanics, Ancona, Italy, 14–17 September 2009

  16. Carpinteri A, Cornetti P, Sapora A (2011) A fractional calculus approach to nonlocal elasticity. Eur Phys J 193:193–204

    Google Scholar 

  17. Atanackovič TM, Stankovič B (2009) Generalized wave equation in nonlocal elasticity. Acta Mech 208:1–10

    Article  MATH  Google Scholar 

  18. Cottone G, Di Paola M, Zingales M (2009) Elastic waves propagation in 1D fractional non-local continuum. Phys E 42:95–103

    Article  Google Scholar 

  19. Sapora A, Cornetti P, Carpinteri A (2013) Wave propagation in nonlocal elastic continua modelled by a fractional calculus approach. Commun Nonlinear Sci Numer Simul 18:63–74

    Article  MathSciNet  MATH  ADS  Google Scholar 

  20. Challamel N, Zorica D, Atanackovič TM, Spasič DT (2013) On the fractional generalization of Eringen’s nonlocal elasticity for wave propagation. C R Mec 341:298–303

    Article  ADS  Google Scholar 

  21. Drapaca CS, Sivaloganathan S (2012) A fractional model of continuum mechanics. J Elast 107:105–123

    Article  MathSciNet  MATH  Google Scholar 

  22. Tarasov VE (2006) Continuous limit of discrete systems with long-range interaction. J Phys A 39:14895–14910

    Article  MathSciNet  MATH  ADS  Google Scholar 

  23. Tarasov VE (2013) Lattice model with power-law spatial dispersion for fractional elasticity. Cent Eur J Phys 11:1580–1588

    Article  Google Scholar 

  24. Oldham KB, Spanier J (1974) The fractional calculus. Academic Press, New York

    MATH  Google Scholar 

  25. Samko G, Kilbas AA, Marichev OI (1993) Fractional integrals and derivatives. Gordon and Breach, Amsterdam

    MATH  Google Scholar 

  26. Podlubny I (1999) Fractional differential equations. Academic Press, San Diego

    MATH  Google Scholar 

  27. Agrawal OP (2007) Fractional variational calculus in terms of Riesz fractional derivatives. J Phys A 40:6287–6303

    Article  MathSciNet  MATH  ADS  Google Scholar 

  28. Gorenflo R, Mainardi F (2001) Random walk models approximating symmetric space-fractional diffusion processes. In: Elschner J, Gohberg I, Silbermann B (eds) Problems in mathematical physics (Siegfried Prössdorf Memorial Volume). Birkhäuser Verlag, Boston-Basel-Berlin, pp 120–145

    Chapter  Google Scholar 

  29. Mainardi F, Gorenflo R, Moretti D, Pagnini G, Paradisi P (2002) Discrete random walk models for space-time fractional diffusion. Chem Phys 284:521–541

    Article  ADS  Google Scholar 

  30. Ortigueira MD (2008) Fractional central differences and derivatives. J Vib Control 14:1255–1266

    Article  MathSciNet  MATH  Google Scholar 

  31. Kröner E (1967) Elasticity theory of materials with long range cohesive forces. Int J Solids Struct 3:731–742

    Article  MATH  Google Scholar 

  32. Eringen AC (1978) Line crack subjected to shear. Int J Fract 14:367–379

    Article  MathSciNet  Google Scholar 

  33. Polizzotto C (2001) Non local elasticity and related variational principles. Int J Solids Struct 38:7359–7380

    Article  MathSciNet  MATH  Google Scholar 

  34. Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48:175–209

    Article  MathSciNet  MATH  ADS  Google Scholar 

  35. Silling SA, Zimmermann M, Abeyaratne R (2003) Deformation of a peridynamic bar. J Elast 73:173–190

    Article  MathSciNet  MATH  Google Scholar 

  36. Aifantis EC (1999) Gradient deformation models at nano, micro, and macro scales. J Eng Mater 121:189–202

    Google Scholar 

  37. Metrikine AV, Askes H (2002) One-dimensional dynamically consistent gradient elasticity models derived from a discrete microstructure. Part 1: generic formulation. Eur J Mech A 21:555–572

    Article  MATH  Google Scholar 

  38. Sumelka W, Blaszczyk T (2014) Fractional continua for linear elasticity. Arch Mech 66:147–172

    MATH  Google Scholar 

  39. Carpinteri A, Mainardi F (1997) Fractals and fractional calculus in continuum mechanics. Springer-Verlag, Wien

    Book  MATH  Google Scholar 

  40. Yang Q, Liu F, Turner I (2010) Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl Math Model 34:200–218

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Structural, Building and Geotechnical Engineering, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Turin, Italy

    Alberto Carpinteri, Pietro Cornetti & Alberto Sapora

Authors
  1. Alberto Carpinteri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pietro Cornetti
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alberto Sapora
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pietro Cornetti.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Carpinteri, A., Cornetti, P. & Sapora, A. Nonlocal elasticity: an approach based on fractional calculus. Meccanica 49, 2551–2569 (2014). https://doi.org/10.1007/s11012-014-0044-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-014-0044-5

Keywords

Search

Navigation