Abstract
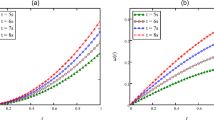
The exact solutions for the motion of a Maxwell fluid due to longitudinal and torsional oscillations of an infinite circular cylinder are determined by means of the Laplace transform. These solutions are presented as sum of the steady-state and transient solutions and describe the motion of the fluid for some time after its initiation. After that time, when the transients disappear, the motion is described by the steady-state solution which is periodic in time and independent of the initial conditions. Finally, by means of graphical illustrations, the required times to reach the steady-state are determined for sine, cosine and combined oscillations of the boundary.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Stokes GG (1886) On the effect of the rotation of cylinders and spheres about their axes in increasing the logarithmic decrement of the arc of vibration. Cambridge University Press, Cambridge
Casarella MJ, Laura PA (1969) Drag on oscillating rod with longitudinal and torsional motion. J Hydronaut 3:180–183
Rajagopal KR (1983) Longitudinal and torsional oscillations of a rod in a non-Newtonian fluid. Acta Mech 49:281–285
Rajagopal KR, Bhatnagar RK (1995) Exact solutions for some simple flows of an Oldroyd-B fluid. Acta Mech 113:233–239
Penton R (1968) The transient for Stokes’ oscillating plane: a solution in terms of tabulated functions. J Fluid Mech 31:819–825
Erdogan ME (2000) A note on an unsteady flow of a viscous fluid due to an oscillating plane wall. Int J Non-Linear Mech 35:1–6
Fetecau C, Fetecau Corina (2005) Starting solutions for some unsteady unidirectional flows of a second grade fluid. Int J Eng Sci 43:781–789
Fetecau C, Fetecau Corina (2006) Starting solutions for the motion of a second grade fluid due to longitudinal and torsional oscillations of a circular cylinder. Int J Eng Sci 44(11–12):788–796
Dapra I, Scarpi G (2006) Pulsatile pipe flows of pseudoplastic fluids. Meccanica 41:501–508
Asghar S, Hanif K, Hayat T (2007) The effect of the slip condition on unsteady flow due to non-coaxial rotations of disk and a fluid at infinity. Meccanica 42(2):141–148
Böhme G (1981) Strömungsmechanik nicht-newtonscher fluide. Teubner, Stuttgart
Fetecau C (2004) Analytical solutions for non-Newtonian fluid flows in pipe-like domains. Int J Non-Linear Mech 39:225–231
Srivastava PM (1966) Non-steady helical flow of a visco-elastic liquid. Arch Mech Stos 2(18):145–150
Tan W, Masuoka T (2005) Stokes’ first problem for an Oldroyd-B fluid in a porous half space. Phys Fluids 17(2):023101–123107
Aksel N, Fetecau C, Scholle M (2006) Starting solutions for some unsteady unidirectional flows of Oldroyd-B fluids. ZAMP 57:815–831
Bandelli R, Rajagopal KR (1995) Start-up flows of second grade fluids in domains with one finite dimension. Int J Non-Linear Mech 30:817–839
Waters ND, King MJ (1970) Unsteady flow of an elastico-viscous liquid. Rheol Acta 9(3):345–355
Ting TW (1963) Certain unsteady flows of second order fluids. Arch Ration Mech Anal 14:1–26
Churchill RV (1972) Operational mathematics. McGraw-Hill, New York
Gray A, Matthews GB (1966) A treatise on Bessel functions and their applications. Dover, New York
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vieru, D., Akhtar, W., Fetecau, C. et al. Starting solutions for the oscillating motion of a Maxwell fluid in cylindrical domains. Meccanica 42, 573–583 (2007). https://doi.org/10.1007/s11012-007-9081-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-007-9081-7