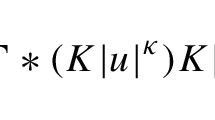Derivation of Isothermal Quantum Fluid Equations with Fermi-Dirac and Bose-Einstein Statistics

Abstract

By using the quantum maximum entropy principle we formally derive, from a underlying kinetic description, isothermal (hydrodynamic and diffusive) quantum fluid equations for particles with Fermi-Dirac and Bose-Einstein statistics. A semiclassical expansion of the quantum fluid equations, up to $\mathcal{O}(\hbar^{2})$-terms, leads to classical fluid equations with statistics-dependent quantum corrections, including a modified Bohm potential. The Maxwell-Boltzmann limit and the zero temperature limit are eventually discussed.

Appendices

Appendix A: Moments of Fermi and Bose Distributions and Related Integrals

We recall that the polylogarithm of order s, with s∈ℝ, is defined in the complex unit disc by the power series

$$\operatorname {\mathrm {Li}}_s(z) = \sum_{k=1}^\infty \frac{z^k}{k^s}, \quad {\vert {z} \vert } < 1, $$

and can be analytically continued to a larger domain (depending on s). To our purposes it will be enough to know that $\operatorname {\mathrm {Li}}_{s}(z)$ is always well defined, real-valued and regular for z∈(−∞,1), and

$$ \lim_{z \to 1^-} \operatorname {\mathrm {Li}}_s(z) = \left\{ \begin{array}{l@{\quad }l} \zeta(s),& \mbox{if }s>1,\\[5pt] +\infty, &\mbox{if }s \leq 1, \end{array} \right. $$

(A.1)

where ζ is the Riemann zeta function. The polylogarithms are strictly connected with the moments of FD and BE distributions.

Definition A.1

For λe^z>−1, $\lambda \not= 0$, and s∈ℝ we define

$$ \phi_s(z) = - \frac{1}{\lambda } \operatorname {\mathrm {Li}}_s \bigl(-\lambda \mathrm {e}^z\bigr), $$

(A.2)

where $\operatorname {\mathrm {Li}}_{s}$ is the polylogarithm of order s. From known identities [24] we have that, for s>0, the above definition is equivalent to

$$ \phi_s(z) = \frac{1}{\varGamma(s)} \int _0^\infty \frac{t^{s-1}}{e^{t-z} + \lambda }\,dt \quad (s > 0) $$

(A.3)

(known as Fermi integral).

Note that ϕ _s (z) is defined for all z∈ℝ if λ>0, and for z<−log|λ| if λ<0. In particular, in the FD case, λ=1, ϕ _s (z) is defined on the whole real line while in the BE case, λ=−1, only for z<0.

The following properties of the functions ϕ _s can be easily deduced from the properties of polylogarithms (see e.g. Refs. [24, 31]):

(A.4a)

(A.4b)

(A.4c)

(A.4d)

(A.4e)

Here, “f(x)∼g(x) for x→y” means lim _x→y f(x)/g(x)=1.

Starting from the identity (A.3), we shall now compute explicit expressions, in terms of the functions ϕ _s , of all the kinds of integrals that have been encountered throughout this paper.

Lemma A.1

For λe^z>−1, k=1,2,3,… and s>0, let us consider the integrals

$$ I_k^s(z) = \frac{1}{\varGamma(s)} \int _0^\infty \frac{t^{s-1}}{ (\mathrm {e}^{t-z} + \lambda )^k}\,dt. $$

(A.5)

Then, $I_{1}^{s}$ is given by Eq. (A.3) and higher values of k are recursively obtained by

$$ I_{k+1}^s(z) = \frac{1}{\lambda} \biggl( I_k^s(z) - \frac{1}{k} \frac{dI_k^s}{dz}(z) \biggr). $$

(A.6)

In particular (omitting the argument z),

$$ \everymath{\displaystyle }\begin{array}{l} I_1^s = \phi_s,\\[5pt] I_2^s = \lambda ^{-1} (\phi_s - \phi_{s-1} ),\\[5pt] I_3^s =\lambda ^{-2} \biggl(\phi_s - \frac{3}{2}\phi_{s-1} + \frac{1}{2}\phi_{s-2} \biggr),\\[8pt] I_4^s = \lambda ^{-3} \biggl(\phi_s - \frac{11}{6}\phi_{s-1} + \phi_{s-2} - \frac{1}{6}\phi_{s-3} \biggr). \end{array} $$

(A.7)

Proof

The recursive formula (A.6) follows immediately from a formal derivation of $I_{k}^{s}(z)$ with respect to z; Eq. (A.7) follows from (A.3) and (A.6) by using the property (A.4e). □

Equation (A.7) suggests that we can look for an expression for $I_{k}^{s}$ of this kind:

$$ I_k^s = \frac{1}{\lambda^{k-1}} \sum _{j=0}^{k-1} c^k_j \phi_{s-j}, \quad k \geq 1, $$

(A.8)

where $c^{k}_{j}$ are numerical coefficients (independent on s) to be determined. Since

$$ \frac{d I_k^s}{dz}(z) = I_k^{s-1}(z) $$

(A.9)

(as it is apparent from Lemma A.1), from the recursive relation (A.6) we can write the equivalent relation

$$ I_{k+1}^s = \frac{1}{\lambda} \biggl( I_k^s - \frac{1}{k} I_k^{s-1} \biggr). $$

(A.10)

Inserting (A.8) into (A.10) yields

$$\sum_{j=0}^{k} c^{k+1}_j \phi_{s-j} = \sum_{j=0}^{k-1} c^k_j \phi_{s-j} - \frac{1}{k}\sum_{j=1}^{k} c^k_{j-1} \phi_{s-j}, \quad k \geq 2. $$

Equating the coefficients of ϕ _s (j=0) we obtain $c^{k+1}_{0} = c^{k}_{0}$, and then (since $c^{1}_{0} = 1$, as follows form (A.8) with k=1)

$$ c^k_0 = 1, \quad k \geq 1; $$

(A.11a)

equating the coefficients of ϕ _s−k (j=k) we obtain $c^{k+1}_{k} = - \frac{1}{k} c^{k}_{k-1}$, and then

$$ c^k_{k-1} = \frac{(-1)^k}{(k-1)!}, \quad k \geq 1; $$

(A.11b)

finally, equating the coefficients of ϕ _s−j , with 1≤j≤k−1, we obtain

$$ c^{k+1}_j = c^k_j - \frac{1}{k} c^k_{j-1}, \quad k \geq 1,\ 1 \leq j \leq k-1. $$

(A.11c)

By using the recursive relations (A.11a)–(A.11c) one can easily generate all the coefficients of the expansion (A.8).

Proposition A.1

Let $I_{k}^{s}(z)$ be given as in the previous lemma. Then,

(A.12a)

(A.12b)

(A.12c)

where, as usual, $n_{d} := (2\pi T)^{\frac{d}{2}}$.

Proof

By using polar coordinates it is easily shown that

$$ \int_{\mathbb {R}^d} \frac{{\vert {p} \vert }^{2m}}{ (\mathrm {e}^{\frac{{\vert {p} \vert }^2}{2T} - z} + \lambda )^k}\,dp = \frac{ n_d\, (2T)^m \varGamma(\frac{d}{2}+m)}{\varGamma(\frac{d}{2})}\, I_k^{\frac{d}{2}+m}(z). $$

(A.13)

This formula immediately yields Eq. (A.12a) and, by obvious symmetry considerations, Eq. (A.12b). The derivation of Eq. (A.12c) requires more explanations. We first show that

$$ J_d(z) := \int_{\mathbb {R}^d} \frac{p_i^4}{ (\mathrm {e}^{\frac{{\vert {p} \vert }^2}{2T} - z} + \lambda )^k}\,dp = 3 n_d T^2 I_k^{\frac{d}{2}+2}(z) $$

(A.14)

(which is of course independent on i). We proceed by double induction on d. The cases d=1,2 can be easily verified by direct computations. Then, assuming (A.14) to be valid for d, for d+2 we can write

$$J_{d+2}(z) = \int_{\mathbb {R}^2} J_d \biggl(z-\frac{{\vert {q} \vert }^2}{2T} \biggr) \,dq = 3 n_d 2\pi T^2 \int_0^\infty I_k^{\frac{d}{2}+2} \biggl(z - \frac{\rho^2}{2T} \biggr) \rho \,d\rho. $$

From Eq. (A.9) we obtain therefore

$$J_{d+2}(z) = 3 n_d 2\pi T^3 I_k^{\frac{d}{2}+3} \biggl(z - \frac{\rho^2}{2T} \biggr) \bigg|^0_{+\infty} = 3 n_{d+2} T^2 I_k^{\frac{d+2}{2}+2}(z), $$

which proves (A.14) by induction. On the other hand, Eq. (A.13) yields

$$\int_{\mathbb {R}^d} \frac{{\vert {p} \vert }^4}{ (\mathrm {e}^{\frac{{\vert {p} \vert }^2}{2T} - z} + \lambda )^k}\,dp = d(d+2)n_d T^2 I_k^{\frac{d}{2}+m}(z) $$

and then, using ${\vert {p} \vert }^{4} = ( \sum_{i} p_{i}^{2} )^{2} = \sum_{i} p_{i}^{4} + \sum_{i\not=j} p_{i}^{2}p_{j}^{2}$ (and symmetry considerations), we obtain

$$ \int_{\mathbb {R}^d} \frac{p_i^2 p_j^2}{ (\mathrm {e}^{\frac{{\vert {p} \vert }^2}{2T} - z} + \lambda )^k}\,dp = n_d T^2 I_k^{\frac{d}{2}+2}(z) $$

(A.15)

for $i \not= j$. The two cases, (A.14) and (A.15), are summarized by (A.12c). □

Appendix B: Postponed Proofs

2.1 B.1 Proof of Proposition 2.1

According to the short notations adopted from Sect. 3.1 on, let us denote $\mathcal {G}_{A,B}$ by $\mathcal {G}$ and $\frac{1}{T}h_{A,B}$ by h (definition (3.1)). Recalling, moreover, the formalism introduced in Sect. 2.1, we can write

where we used the fact that $\operatorname {Op}_{\epsilon }(\mathcal {G})$ is, by definition (2.31), a function of $\operatorname {Op}_{\epsilon }(h )$ and then $\{h,\mathcal {G}\}_{\#}= 0$, because it is the inverse Weyl quantization of a vanishing commutator. Since, from a direct computation,

$$\frac{i}{\epsilon } \{p_j B_j, \mathcal {G}\}_\# = - p_j \frac{\partial B_j}{\partial x_k} \frac{\partial \mathcal {G}}{\partial p_k} + B_j \frac{\partial \mathcal {G}}{\partial x_j}, $$

then from the previous identity we have

(where Eq. (2.20) was used), which yields Eq. (2.32).  □

2.2 B.2 Proof of Lemma 3.1

Lemma 3.1 follows from elementary manipulations of formal Taylor expansions. In order to shorten the notations, let us introduce the (d+1)-dimensional vectors

The constraint system (3.6), in these notations, reads as follows:

$$ f(\mu) = m. $$

(B.1)

Note that f has a double dependence on ϵ: one is direct (which leads to the expansion (3.2), i.e. to the terms f ^(k)), and the other is through the Lagrange multipliers, which are expanded as μ=μ ⁽⁰⁾+ϵμ ⁽¹⁾+ϵ ² μ ⁽²⁾+⋯. Then, we regard f as f(ϵ,μ(ϵ)), whose Taylor expansion at ϵ=0 can be written in this way:

(where we took into account that f ⁽¹⁾=0, from (3.4b), and, for the sake brevity, the third-order term was not shown). Since the moments m do not depend on ϵ, the constraint equation (B.1) is expanded as follows:

The first equation is Eq. (3.8a), the second one implies μ ⁽¹⁾=0 (i.e. A ⁽¹⁾=B ⁽¹⁾=0), the third one is Eq. (3.8b) and, finally, the fourth one (which has been omitted for brevity) implies μ ⁽³⁾=0 (i.e. A ⁽³⁾=B ⁽³⁾=0).  □

2.3 B.3 Proof of Lemma 3.2

By using Eq. (3.4c) with n=1 we obtain

$$ \mathcal {G}_2 = - \frac{\mathcal {G}_0\, \operatorname {\mathcal {E}\!\mathit {xp}}_2(h) + \mathcal {G}_0\mathbin{\#_2}\mathrm {e}^h}{\mathrm {e}^h + \lambda }. $$

(B.2)

The first term contains $\operatorname {\mathcal {E}\!\mathit {xp}}_{2}(h)$, whose explicit expression can be taken from Eq. (5.14) of Ref. [10] and reads as follows:

$$ \operatorname {\mathcal {E}\!\mathit {xp}}_2(h) = -\frac{\mathrm {e}^h}{8} \biggl( X_{ij} P_{ij} - S_{ij}S_{ji} + \textstyle{\frac{1}{3}} X_{ij}P_iP_j - \textstyle{\frac{2}{3}} S_{ij}P_iX_j + \textstyle{\frac{1}{3}} P_{ij}X_iX_j \biggr), $$

(B.3)

where we introduced the following notations:

(we recall that $h = \frac{1}{T} h_{A,B}$ is given by (3.1)). The other term, $\mathcal {G}_{0}\,\#_{2}\,\mathrm {e}^{h}$, is a second-order Moyal product, given by (2.5). Using the notations just introduced, we obtain:

where, for k≥0, we define

$$ F_k = \frac{\mathrm {e}^{kh}}{(\mathrm {e}^h + \lambda )^{k+1}}. $$

(B.4)

Putting together the two terms we obtain the following expression for $\mathcal {G}_{2}$:

(B.5)

Note that in the Maxwell-Boltzmann case, λ=0, we have F _k =e^−h for all k≥0 and, therefore,

Then, in this case, Eq. (B.5) reduces (as it should) to $\operatorname {\mathcal {E}\!\mathit {xp}}_{2}(-h)$, which is given by (B.3) with the suitable changes of sign.

Now, defining q=p−B, taking the moments ${\langle \mathcal {G}_{2} \rangle }$ and ${\langle q_{i} \mathcal {G}_{2} \rangle }$ from Eq. (B.5), and taking account of vanishing integrals of odd functions, we get

(B.6)

and

(B.7)

The moments of functions F _k can be reduced to integrals of type $I_{k}^{s}$ (see Lemma A.1) by using

$$ F_k = \frac{1}{\mathrm {e}^h + \lambda } \biggl(1 - \frac{\lambda }{\mathrm {e}^h + \lambda } \biggr)^k = \sum_{j=0}^k {k \choose j} \frac{(-\lambda )^j}{(\mathrm {e}^h + \lambda )^{j+1}}. $$

(B.8)

Recalling that

$$h = \frac{{\vert {q} \vert }^2}{2T} - \frac{A}{T}, $$

from (B.8) and (A.12a)–(A.12c) we obtain

Then, by using ${\langle p_{i}\mathcal {G}_{2} \rangle } = B_{i}{\langle \mathcal {G}_{2} \rangle } + {\langle q_{i}\mathcal {G}_{2} \rangle }$ and the identity

(from property (A.4e)), Eqs. (3.12a)–(3.12b) are easily obtained from the expressions (B.6) and (B.7).  □