Skip to main content
SpringerLink
Log in

Ducks on the torus: existence and uniqueness

  • Published:
Journal of Dynamical and Control Systems Aims and scope Submit manuscript

Abstract

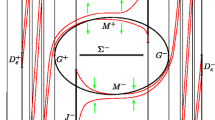
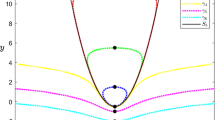
We show that there exist generic slow-fast systems with only one (time-scaling) parameter on the two-torus, which have canard cycles for arbitrary small values of this parameter. This is in drastic contrast with the planar case, where canards usually occur in two-parametric families. Here we treat systems with a convex slow curve. In this case there is a set of parameter values accumulating to zero for which the system has exactly one attracting and one repelling canard cycle. The basin of the attracting cycle is almost the whole torus.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. O. Anosova, On invariant manifolds in singulalry perturbed systems. J. Dynam. Control Syst. 5 (1999), No. 4, 501–507.

    Article  MATH  MathSciNet  Google Scholar 

  2. _____, Invariant manifolds in singularly perturbed systems. Proc. Steklov Math. Inst. 236 (2002), 19–24.

    MathSciNet  Google Scholar 

  3. A. Denjoy, Sur les courbes définies par des équations différentielles à la surface du tore. J. Math. Pure Appl. 11 (1932), 333–375.

    MATH  Google Scholar 

  4. M. Diener, The canard unchained or how fast/slow dynamical systems bifurcate. Math. Intel. 6 (1984), 38–48.

    Article  MATH  MathSciNet  Google Scholar 

  5. F. Dumortier and R. Roussarie, Canard cycles and center manifolds. Mem. Amer. Math. Soc. 121 (1996).

  6. N. Fenichel, Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equations 31 (1979), 53–98.

    Article  MATH  MathSciNet  Google Scholar 

  7. J. Guckenheimer and Yu. S. Ilyashenko, The duck and the devil: canards on the staircase. Moscow Math. J. 1 (2001), No. 1, 27–47.

    MATH  MathSciNet  Google Scholar 

  8. M. Krupa and P. Szmolyan, Extending geometric singular perturbation theory to nonhyperbolic points — fold and canard points in two dimensions. SIAM J. Math. Anal. 33, No. 2, 286–314.

  9. E. F. Mishchenko and N. Kh. Rozov, Differential equations with small parameters and relaxation oscillations. Plenum Press, New York (1980).

    MATH  Google Scholar 

  10. A. Schwartz, A generalization of Poincaré–Bendixon theorem to closed two dimensional manifolds. Amer. J. Math. 85 (1963), 453–458.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Moscow State University, Moscow, Russia

    I. V. Schurov

Authors
  1. I. V. Schurov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. V. Schurov.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Schurov, I.V. Ducks on the torus: existence and uniqueness. J Dyn Control Syst 16, 267–300 (2010). https://doi.org/10.1007/s10883-010-9093-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10883-010-9093-9

Key words

2000 Mathematics Subject Classification

Search

Navigation