An Interaction-Free Quantum Measurement-Driven Engine

Abstract

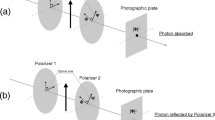
Recently highly-efficient quantum engines were devised by exploiting the stochastic energy changes induced by quantum measurement. Here we show that such an engine can be based on an interaction-free measurement, in which the meter seemingly does not interact with the measured object. We use a modified version of the Elitzur–Vaidman bomb tester, an interferometric setup able to detect the presence of a bomb triggered by a single photon without exploding it. In our case, a quantum bomb subject to a gravitational force is initially in a superposition of being inside and outside one of the interferometer arms. We show that the bomb can be lifted without blowing up. This occurs when a photon traversing the interferometer is detected at a port that is always dark when the bomb is located outside the arm. The required potential energy is provided by the photon (which plays the role of the meter) even though it was not absorbed by the bomb. A natural interpretation is that the photon traveled through the arm which does not contain the bomb—otherwise the bomb would have exploded—but it implies the surprising conclusion that the energy exchange occurred at a distance despite a local interaction Hamiltonian. We use the weak value formalism to support this interpretation and find evidence of contextuality. Regardless of interpretation, this interaction-free quantum measurement engine is able to lift the most sensitive bomb without setting it off.

Appendices

Appendix A: Inside and Outside States

The quantum bouncing ball Hamiltonian $H_{\text {m}}$ corresponds to a potential $V_{\text {m}}(z) = mgz$ for $z>0,$ and infinite for $z\le 0.$ The wavefunction of the energy eigenstates of $H_{\text {m}},$ i.e. $| j \rangle _{\text {m}}$ with j an integer, can be expressed given in term of the Airy function ${{\mathcal {A}}}(u)$ which is the solution of the ODE $\frac{d^{2}}{du^{2}}y(u)-u y(u)=0$ which does not diverge for $u\rightarrow \infty$:

$$\psi _{\text {m}}^{(j)}(z) = \langle z | j \rangle _{\text {m}} = \frac{{{\mathcal {A}}}(z/z_{0}+\zeta _{j+1})}{{{\mathcal {A}}}'(\zeta _{j+1})},$$

(15)

where $z_{0} = (\hbar ^{2}/2m^{2}g)^{1/3}$ is a characteristic length of the problem and $\zeta _{j}$ is the jth zero of the Airy function (which is negative). We consider that the atom is in the ground state $| 0 \rangle _{\text {m}}$ and one sends a photon towards it. The photon spatial wavefunction has a Gaussian shape in the z direction $\phi _{0}(z).$ The photon and the atom interaction strength is proportional to the spatial overlap of their wavefunctions, such that $\phi _{0}(z)$ can be seen as the atom wavefunction that optimally interacts with the photon. It turns out that a Gaussian wavefunction $\chi (z)$ of average ${\bar{z}} = 2.80 z_{0}$ and standard deviation ${\bar{\sigma }} = 1.27x_{0}$ coincides almost exactly with that of the state $| - \rangle _{\text {m}} =(| 0 \rangle _{\text {m}}-| 1 \rangle _{\text {m}})/\sqrt{2},$ as quantified by an overlap probability $(\int dz\chi (z)\langle z | - \rangle _{\text {m}})^{2} \simeq 0.99.$ This justifies Eqs. (1)–(2) of the main text defining states $| \text {in} \rangle$ and $| \text {out} \rangle .$ While a similar analysis can be done for an arbitrary superposition of the states $| 0 \rangle _{\text {m}}$ and $| 1 \rangle _{\text {m}}$ being coupled to the photon, this particular choice simplifies the calculation and clarifies the analysis.

As an interesting additional feature, the wavefunction of state $| \text {in} \rangle _{\text {m}}$ turns out to be negligible in the vicinity of the platform up to $z\sim z_{0}/2.$ As a consequence, once the bomb has been projected onto this state, it is possible to raise the floor level of an amount $\varDelta z \le z_{0}/2$ without paying work to raise the bomb, therefore storing usefull gravitational potential energy [12].

Appendix B: Photon–Bomb Interaction

The bomb is a zero temperature reservoir, modeled by a collection of harmonic modes $b_{k}$ at frequency $\nu _{k}.$ The photon modes are denoted $a_{j}$ with frequencies $\omega _{j}.$ The coupling Hamiltonian reads:

$$V = i \varPi _{\text {in}}\sum _{j,k}g_{k}(a_{j}^{\dagger } b_{k} - b_{k}^{\dagger } a_{j}).$$

(16)

We consider the weak coupling limit $\vert g_{k}\vert \tau _c\ll 1$ where $\tau _{c}$ it the correlation time of the bomb and assume a coupling independent of the photon’s frequency for simplicity. We model the evolution the following way: the photon and the bomb interact during $\varDelta t$ fulfilling $\tau _c\ll \varDelta t\ll \tau ,$ then the number of excitations in the bomb is checked. In addition, we work in the limit:

$$\omega _{\text {ph}}^{-1},\varDelta \omega _{\text {ph}}^{-1},\omega _{\text {b}}^{-1},\omega _{\text {m}}^{-1} \ll \varDelta t \ll \varGamma ^{-1} ,$$

(17)

where

$$\varGamma = \sum _{k} g_{k}^{2} \delta (\omega _{\text {ph}}-\omega _{k}),$$

(18)

is the effective rate of the evolution induced by the interaction, as shown below.

We work in the interaction picture (denoted with tilde) where the coupling Hamiltonian fulfils:

$${\tilde{V}}(t) = i {\tilde{\varPi }}_{\text {in}}(t)\sum _{j,k}g_{k}(a_{j}^{\dagger } b_{k} e^{i (\omega _{j}-\nu _{k}) t} - b_{k}^{\dagger } a_{j}e^{i(\nu _{k}-\omega _{j})t}).$$

(19)

Starting from the state $| {\tilde{\varPsi }}(t) \rangle = | {\tilde{\phi }}(t) \rangle _{\text {ph}}| {\tilde{\chi }}(t) \rangle _{\text {m}}| 0 \rangle _{\text {b}}$ and the bomb in the vacuum $| 0 \rangle _{\text {b}},$ the evolved state, after the bomb is found containing n excitations, reads at second order in $\varDelta t$:

$$\begin{aligned} | {\tilde{\varPsi }}(t+\varDelta t) \rangle= & {} \delta _{n,0}| {\tilde{\varPsi }}(t) \rangle -i\int _{t}^{t+\varDelta t}dt' {}_{\text {b}}\langle n |\tilde{V}(t')| 0 \rangle _{\text {b}}| {\tilde{\varPsi }}(t) \rangle \\&- \frac{1}{2}\int _{t}^{t+\varDelta t}dt'\int _{t}^{t'}dt''{}_{\text {b}}\langle n |{\tilde{V}}(t')\tilde{V}(t'')| 0 \rangle _{\text {b}}| {\tilde{\varPsi }}(t) \rangle . \end{aligned}$$

(20)

We focus to the case $n=0$ (bomb not exploded), such that the term in first order in ${\tilde{V}}$ vanishes. Denoting ${\tilde{M}}_{0}$ the Kraus operator updating the wavefunction in this case, we get:

$$\begin{aligned} {\tilde{M}}_{0}= & {} 1- \frac{1}{2}\int _{t}^{t+\varDelta t}dt'\int _{t}^{t'}dt''{}_{\text {b}}\langle n |{\tilde{V}}(t')\tilde{V}(t'')| 0 \rangle _{\text {b}} \\= & {} 1+ \frac{1}{2}\int _{t}^{t+\varDelta t}\!\!\!\!\!\!\!\!dt'\int _{0}^{t'-t}\!\!\!\!\!\!d\tau e^{i(\omega _{i}-\omega _{k})t'}e^{i(\omega _{k}-\omega _{j})(t'-\tau )} \\&\quad \times \sum _{i,j,k}g_{k}^{2} a_{i}^{\dagger } a_{j} {\tilde{\varPi }}_{\text {in}}(t'){\tilde{\varPi }}_{\text {in}}(t'-\tau ). \end{aligned}$$

(21)

We now use that ${\tilde{\varPi }}_{\text {in}}(t) = (1/2)(\mathbb {1}- \sigma _{\text {m}}e^{-i\omega _{\text {m}}t}- \sigma _{\text {m}}^{\dagger } e^{i\omega _{\text {m}}t})$ and that the bomb correlation time is assumed to be much smaller than $\varDelta t.$ This allows us to replace the upper bound of the integral over $\tau$ by $+\infty .$ This integral can then be computed and yields Dirac distributions, forming the bomb spectral density taken at various frequencies, i.e. $S(\omega ) = \sum _{k} g_{k}^{2}\delta (\omega -\omega _k),$ where $\omega$ takes typical values in the range $[\omega _{\text {ph}}-\varDelta \omega _{\text {ph}},\omega _{\text {ph}}+\varDelta \omega _{\text {ph}}],$ i.e. the frequencies typically contained in the initial photon state. We assume that the bomb spectral density is flat on this frequency range, such that we can replace $S(\omega )$ with $\varGamma$ defined in Eq. (18). Finally, apply the Secular approximation [34], i.e. we neglect in the integral over $t'$ all the term rotating at non-zero frequency. We finally get (back in Scrödinger picture):

$$\begin{aligned} M_{0} -\mathbb {1}= & {} -i(H_{\text {m}}+H_{\text {ph}})dt- \frac{\varGamma }{4}\sum _{ij}a_{i}^{\dagger } a_{j}\left[ \delta (\omega _{i}-\omega _{j})\right. \\&\left. \quad -\sigma _{\text {m}}\delta (\omega _{i}-\omega _{j}-\omega _{\text {m}})-\sigma _{\text {m}}^{\dagger }\delta (\omega _{i}-\omega _{j}+\omega _{\text {m}}))\right] \end{aligned}$$

(22)

This Kraus operator solely couples states $| \omega _{j} \rangle _{\text {ph}}| 0 \rangle _{\text {m}}| 0 \rangle _{\text {b}}$ to $| \omega _{j}-\omega _{\text {m}} \rangle _{\text {ph}}| 1 \rangle _{\text {m}}| 0 \rangle _{\text {b}}$. As a consequence, if one assumes the Ansatz,

$$\begin{aligned} | {\tilde{\varPsi }}(\tau ) \rangle= & {} \sum _{j}\left[ c_{0}(\tau )\phi _{0}(\omega _{j})| 0 \rangle _{\text {m}}\right. \\&\left. \quad + c_{1}(\tau )\phi _{0}(\omega _{j}+\omega _{\text {m}})| 1 \rangle _{\text {m}}\right] a_{I,j}^{\dagger }| 0 \rangle _{\text {ph}}| -0 \rangle _{\text {b}}, \end{aligned}$$

(23)

where $\phi _{0}(\omega )$ is the initial photon wavefunction, one finds that the amplitudes $c_{0}$ and $c_{1}$ fulfill the evolution equations:

$$\begin{aligned} \dot{c}_{0}= & {} -\frac{\varGamma }{4} (c_{0}-c_{1}), \\ \dot{c}_{1}= & {} \frac{\varGamma }{4} (c_{0}-c_{1}). \end{aligned}$$

(24)

In particular, starting from $c_{0} = 1,$ $c_{0}=0,$ one gets $c_{0,1}(\tau ) = (1\pm e^{-\varGamma \tau /2})/2.$ Finally, the state $| I \rangle _{\text {ph}}| 0 \rangle _{\text {m}}| 0 \rangle _{\text {b}}$ is mapped onto state $\sum _{j}(\phi _{0}(\omega _{j})| 0 \rangle _{\text {m}}+\phi _{0}(\omega _{j}+\omega _{\text {m}})e^{-i\omega _{\text {m}}\tau }| 1 \rangle _{\text {m}})| 0 \rangle _{\text {b}}/\sqrt{2}$ at long times $\tau \gg \varGamma ^{-1}.$ This state can be approximated (after being renormalized) by $| I \rangle _{\text {ph}}| \text {out} \rangle _{\text {m}}| 0 \rangle _{\text {b}}$ provided the two wavefunctions $\phi _{0}(\omega )$ and $\phi _{0}(\omega +\omega _{\text {m}})$ have overlap of almost unity, i.e. provided that the initial photon width $\varDelta \omega _{\text {ph}}$ is much larger than $\omega _{\text {m}}.$

Note that the bomb–photon interaction time $\tau$ is set by the longest of the bomb length and photon duration. The photon duration is constrained by its frequency width $\tau _{\text {ph}}= \varDelta \omega _{\text {ph}}^{-1} \ll \omega _{\text {m}}^{-1}\ll \varGamma ^{-1}.$ Consequently, in order to have $\varGamma \tau > 1,$ we need a large bomb of width $L > c/\varGamma .$

Note also that when written in Schrödinger picture, the system’s state for $\varGamma \tau \gg 1$ actually follows a limiting cycle $| I(\tau ) \rangle | {\text {out}}(\tau ) \rangle _{\text {m}}.$ The time-dependence of the photon state wavefunction solely encode the free propagation of the wavepacket. On the other hand, the bomb motional state evolves $| {\text {out}}(\tau ) \rangle _{\text {m}} =(| 0 \rangle _{\text {m}}+e^{-i\omega _{\text {m}}\tau }| 1 \rangle _{\text {m}})/\sqrt{2},$ i.e. a coherent rotation exchanging states $| \text {out} \rangle _{\text {m}}$ and $| \text {in} \rangle _{\text {m}}$ at frequency $\omega _{\text {m}}.$ In order to obtain state at the end of the protocol $| \text {out} \rangle _{\text {m}},$ one has to keep track of the phase $\omega _{\text {m}}$ accumulated during $\tau$ to correct it by letting the bomb evolve freely during a time $\tau _{2}$ such that $\tau +\tau _{2}$ is a multiple of $2\pi /\omega _{\text {m}}.$

The probability $p_{\text {ne}}(\tau )$ of the bomb not having exploded until time $\tau$ is encoded in the norm of $| {\tilde{\varPsi }}(\tau ) \rangle .$ We find:

$$p_{\text{ne}}(\tau ) = \frac{1}{2}\left( 1+e^{-\varGamma \tau }\right) .$$

(25)

Interferometer setup. When the previous setup is embedded as one of the two arms of an interferometer, the model is modified as follows. The coupling Hamiltonian V is assumed to vanish on the photon subspace corresponding to arm II,  i.e. the space spanned by $\{a_{j}^{\dagger }| 0 \rangle _{\text {ph}}\}_{j}.$ As the consequence, the evolution of the initial state $| \varPsi _{0}' \rangle$ in the interaction picture can be deduced by keeping the term involving state $| II \rangle _{\text {ph}}$ unchanged and applying to the term involving $| I \rangle _{\text {ph}}$ the same evolution as above. The probability of non-explosion in this case can be deduced from Eq. (25) which can be understood as the conditional probability for the bomb not exploding given the photon is initially in arm I. Using that the probability of explosion is zero if the photon is in arm II,  we obtain:

$$p_{\text {ne}}(\tau ) = \frac{1}{2} + \frac{1}{4}\left( 1+e^{-\varGamma \tau }\right) .$$

(26)

The probability of explosion is therefore $p_{\text {expl}}(\tau ) = 1-p_{\text {ne}}(\tau ) = \frac{1}{4}\left( 1-e^{-\varGamma \tau }\right) .$ In order to compute the probability of the dark and bright port detections, we use the conditional probabilities

$$\begin{aligned} p({\text {br}}\vert {\text {ne}})= & {} \vert {}_{\text {m}}\langle \text {br} | {\tilde{\varPsi }}_{2}'(\tau )\rangle \vert ^{2} \\= & {} \frac{5+2e^{-\varGamma \tau /2}+e^{-\varGamma \tau }}{2(3+e^{-\varGamma \tau })}, \end{aligned}$$

(27)

$$\begin{aligned} p({\text {dk}}\vert {\text {ne}})= & {} \vert {}_{\text {m}}\langle \text {dk} | {\tilde{\varPsi }}_{2}'(\tau )\rangle \vert ^{2} \\= & {} \frac{(1-e^{-\varGamma \tau /2})^2}{2(3+e^{-\varGamma \tau })}, \end{aligned}$$

(28)

that the photon is found in the bright and dark port respectively, given the bomb did not explode. The probabilities of these two events is then obtained by multiplying by $p_{\text {ne}}(\tau ),$ allowing to find the expressions given in the main text.

Transmitted photon energy. At the end of the interaction, the photon and bomb are in an entangled state as described by Eq. (6) of the main text. One can compute the energy in the photon going into each port using the beam-splitter relation:

$$\begin{aligned} a^{\dagger }_{I,j}= & {} \frac{1}{\sqrt{2}}(a^{\dagger }_{{\text {br}},j}+a^{\dagger }_{{\text {dk}},j}), \\ a^{\dagger }_{II,j}= & {} \frac{1}{\sqrt{2}}(a^{\dagger }_{{\text {br}},j}-a^{\dagger }_{{\text {dk}},j}), \end{aligned}$$

(29)

where $a^{\dagger }_{{\text {br}},j}$ (resp. $a^{\dagger }_{{\text {dk}},j}$) creates a photon of frequency $\omega _{j}$ at the bright (resp. dark) port. This allows us to express the exact form of the output state, introducing the notation $\phi _{1}(\omega _{j})=\phi _{0}(\omega _{j}+\omega _{\text {m}}),$ namely $| \varPsi '_{2} \rangle \propto$

$$\begin{aligned}&\sum _{j}\left[ \left( \phi _{0}(\omega _{j})\frac{3+e^{-\frac{\varGamma \tau }{2}}}{2}| 0 \rangle _{\text {m}}+ \phi _{1}(\omega _{j})\frac{1-e^{-\frac{\varGamma \tau }{2}}}{2}| 1 \rangle _{\text {m}}\right) a^{\dagger }_{{\text {br}},j}\right. \\&\left. \quad +\frac{1-e^{-\frac{\varGamma \tau }{2}}}{2}\left( -\phi _{0}(\omega _{j})| 0 \rangle _{\text {m}}+ \phi _{1}(\omega _{j})| 1 \rangle _{\text {m}}\right) a^{\dagger }_{{\text {dk}},j}\right] | 0 \rangle _{\text {ph}}| 0 \rangle _{\text {b}}. \end{aligned}$$

(30)

The second (resp. third) line terms in Eq. (30) can be identified (after renormalization) as the joint photon–bomb state $| \varPsi '_{\text {br}} \rangle$ (resp. $| \varPsi '_{\text {dk}} \rangle$) when the photon is found in the bright (resp. dark) port. This enables to compute the corresponding photon energy:

$$\begin{aligned} E_{\text {br}}^{({\text{ph}})}= & {} \sum _{j} {\hbar {\omega }}_{j} \langle \varPsi '_{\text {br}} | a^{\dagger }_{{\text {br}},j}a_{{\text {br}},j}| \varPsi '_{\text {br}} \rangle \\=\, & {} {\hbar {\omega }}_{\text {ph}}-\frac{{\hbar {\omega }}_{\text {m}}}{10} \\ E_{\text {dk}}^{({\text {ph}})}= & {} \sum _{j} {\hbar {\omega }}_{j} \langle \varPsi '_{\text {dk}} | a^{\dagger }_{{\text {dk}},j}a_{{\text {dk}},j}| \varPsi '_{\text {dk}} \rangle \\= \,& {} {\hbar {\omega }}_{\text {ph}}-\frac{{\hbar {\omega }}_{\text {m}}}{2}. \end{aligned}$$

(31)

One can check that the variation of the energy of the photon from its initial energy ${\hbar {\omega }}_{\text {ph}}$ compensates in each case the energy gained by the internal degree of freedom of the bomb:

$$\begin{aligned} E_{\text {br}}^{({\text {m}})}= & {} {\hbar {\omega }}_{\text {m}} \vert {}_{\text {m}}\langle 1 | \varPsi '_{\text {br}} \rangle \vert ^{2} \\= & {} \frac{{\hbar {\omega }}_{\text {m}}}{10} \\ E_{\text {dk}}^{({\text {m}})}= & {} {\hbar {\omega }}_{\text {m}} \vert {}_{\text {m}}\langle 1 | \varPsi '_{\text {dk}} \rangle \vert ^{2} \\=\, & {} \frac{{\hbar {\omega }}_{\text {m}}}{2}. \end{aligned}$$

(32)

Equation (10) of the main text is retrieved by making the approximation $\phi _{1}(\omega _{j})\simeq \phi _{0}(\omega _{j}),$ i.e. neglecting the photon frequency shift with respect to its much larger initial frequency uncertainty. The same approximation allows us to find that $| \varPsi '_{\text {br}} \rangle \simeq | \text {br} \rangle _{\text {ph}}| \phi _{\text {br}} \rangle$ and $| \varPsi '_{\text {dk}} \rangle \simeq | \text {dk} \rangle _{\text {ph}}| \phi _{\text {dk}} \rangle .$

Appendix C: Weak Values

The evolution of the photon-atom state up to time t,  postselecting on the absence of explosion during the interval [0, t],  can be encoded in the propagator:

$${{\mathcal {U}}}(t) = \varPi _{II} + \varPi _{\text {i}} + \varPi _{\text {o}}e^{-\varGamma t/2},$$

(33)

where $\varPi _{II} = \sum _{j} a^{\dagger }_{II,j}| 0 \rangle _{\text {ph}}\langle 0 |a_{j}$ is the projector on arm II,  and $\varPi _{\text {i}}$ (resp. $\varPi _{\text {o}}$) is the projector on state $| \varPhi _{\text {i}} \rangle$ (resp. $| \varPhi _{\text {o}} \rangle$) defined by:

$$\begin{aligned} | \varPhi _{\text {i}} \rangle= & {} \sum _{j}\frac{\phi _{0}(\omega _{j})| 0 \rangle _{\text {m}}- \phi _{0}(\omega _{j}+\omega _{\text {m}})| 1 \rangle _{\text {m}}}{2}a_{I,j}^{\dagger }| 0 \rangle _{\text {ph}}| 0 \rangle _{\text {b}}, \\ | \varPhi _{\text {o}} \rangle= & {} \sum _{j}\frac{\phi _{0}(\omega _{j})| 0 \rangle _{\text {m}}+ \phi _{0}(\omega _{j}+\omega _{\text {m}})| 1 \rangle _{\text {m}}}{2}a_{I,j}^{\dagger }| 0 \rangle _{\text {ph}}| 0 \rangle _{\text {b}}. \end{aligned}$$

(34)

We first compute the weak values associated with the rank 1 projectors $\varPi _{I,{\text {in}}} =| I \rangle _{\text {ph}}\langle I |_{\text {ph}}| \text {in} \rangle _{\text {m}}\langle \text {in} |,$ $\varPi _{I,{\text {out}}} =| I \rangle _{\text {ph}}\langle I |_{\text {ph}}| \text {out} \rangle _{\text {m}}\langle \text {out} |,$ $\varPi _{I,0} =| I \rangle _{\text {ph}}\langle I |_{\text {ph}}| 0 \rangle _{\text {m}}\langle 0 |$ and $\varPi _{I,1} =| I \rangle _{\text {ph}}\langle I |_{\text {ph}}| 1 \rangle _{\text {m}}\langle 1 |$ (and similar for arm II). We obtain:

$$\begin{aligned} \left\langle \varPi _{I,{\text {in}}} \right\rangle _w(t)= & {} -\frac{1}{e^{\varGamma \tau }-1}, \\ \left\langle \varPi _{I,{\text {out}}} \right\rangle _w(t)= & {} 0, \\ \left\langle \varPi _{II,{\text {in}}} \right\rangle _w(t)= & {} 1+\frac{1}{e^{\varGamma \tau }-1}, \\ \left\langle \varPi _{II,{\text {out}}} \right\rangle _{w}(t)= \,& {} 0, \\ \left\langle \varPi _{I,0} \right\rangle _{w}(t)= & {} -\frac{e^{-\varGamma (\tau -t)/2} +e^{-\varGamma \tau /2}}{2(1-e^{-\varGamma \tau /2})}, \\ \left\langle \varPi _{I,1} \right\rangle _{w}(t)= & {} \frac{e^{-\varGamma (\tau -t)/2}-e^{-\varGamma \tau /2} }{2(1-e^{-\varGamma \tau /2})}, \\ \left\langle \varPi _{II,0} \right\rangle _{w}(t)= & {} \frac{1}{1-e^{-\varGamma \tau }}, \\ \left\langle \varPi _{I,1} \right\rangle _{w}(t)= & {} 0. \end{aligned}$$

(35)

One can then deduce the weak values of the rank 2 projectors $\left\langle \varPi _{I} \right\rangle _{w}(t) = \left\langle \varPi _{I,0} \right\rangle _{w}(t)+\left\langle \varPi _{I,1} \right\rangle _{w}(t) =\left\langle \varPi _{I,{\text {in}}} \right\rangle _{w}(t)+\left\langle \varPi _{I,{\text {out}}} \right\rangle _{w}(t) =-1/(1-e^{\varGamma \tau })\simeq 0$ for $\varGamma \tau \gg 1,$ $\left\langle \varPi _{II} \right\rangle _{w}(t)=\left\langle \varPi _{II,0} \right\rangle _{w}(t)+\left\langle \varPi _{II,1} \right\rangle _{w}(t) = 1/(1-e^{-\varGamma \tau }) \simeq 1.$

We then compute the energetic weak-values. Using $H_{\text {m}}={\hbar {\omega }}_{\text {m}}| 1 \rangle _{\text {m}}\langle 1 |,$ one has:

$$\begin{aligned} \left\langle H_{\text {m}} \right\rangle _{w}(t)= \,& {} \left\langle H_{\text {m}}\varPi _{I} \right\rangle (t) \\= \,& {} {\hbar {\omega }}_{\text {m}}\frac{e^{-\varGamma (\tau -t)/2}-e^{-\varGamma \tau /2} }{2(1-e^{-\varGamma \tau /2})} \end{aligned}$$

(36)

$$\left\langle H_{\text {m}}\varPi _{II} \right\rangle (t)= {} 0.$$

(37)

Similarly, one has:

$$\begin{aligned} \left\langle H_{\text {ph}}\varPi _{I} \right\rangle _w(t)= \,& {} {\hbar {\omega }}_{\text {ph}}\left\langle \varPi _{I,0} \right\rangle _{w}(t) \\&\quad +\hbar (\omega _{\text {ph}}-\omega _{\text {m}})\left\langle \varPi _{I,1} \right\rangle _{w}(t), \end{aligned}$$

(38)

$$\begin{aligned} \left\langle H_{\text {ph}}\varPi _{II} \right\rangle _w(t)=\, & {} {\hbar {\omega }}_{\text {ph}}\left\langle \varPi _{II,0} \right\rangle _{w}(t). \end{aligned}$$

(39)

Appendix D: Backward Propagation

In [28], it is pointed out that the interaction-free nature of the measurement process is characterized by a vanishing wavefunction of the photon in the arm I when propagated backward from the dark port. Within our framework, one can compute the evolution of the postselected joint bomb–photon state $| {\tilde{\varPsi }}_{\text {f}} \rangle = | \text {dk} \rangle _{\text {ph}}| \text {in} \rangle _{\text {m}}| 0 \rangle _{\text {b}}.$ Using the same method as in the second section of the “Appendix”, we define the Ansatz wavefunction:

$$\begin{aligned} | {\tilde{\varPsi }}_{\text {bw}}(t) \rangle= & {} \sum _{j}\left[ \left( c'_{0}(\tau )\phi _{0}(\omega _{j})+d'_{0}(\tau )\phi _{0}(\omega _{j}-\omega _{\text {m}})\right) | 0 \rangle _{\text {m}}\right. \\&\left. \quad + \left( c'_{1}(\tau )\phi _{0}(\omega _{j}+\omega _{\text {m}})+d'_{1}(\tau )\phi _{0}(\omega _{j})\right) | 1 \rangle _{\text {m}}\right] a_{I,j}^{\dagger }| 0 \rangle _{\text {ph}}| 0 \rangle _{\text {b}} \\&\quad -\frac{1}{\sqrt{2}}| II \rangle _{\text {ph}}| {\text {in}} \rangle _{\text {m}}| 0 \rangle _{\text {b}}, \end{aligned}$$

(40)

and look for the evolution equation for the coefficients $c'_{0,1}(\tau ),$ $d'_{0,1}(\tau ).$ We obtain:

$$\begin{aligned} \dot{{c}'}_{0}= & {} -\frac{\varGamma }{4}({\tilde{c}}_{0}-{\tilde{c}}_{1}), \end{aligned}$$

(41)

$$\begin{aligned} \dot{{c}'}_{1}= & {} \frac{\varGamma }{4}({\tilde{c}}_{0}-{\tilde{c}}_{1}), \end{aligned}$$

(42)

$$\begin{aligned} \dot{{d}'}_{0}= & {} -\frac{\varGamma }{4}({\tilde{d}}_{0}-{\tilde{d}}_{1}), \end{aligned}$$

(43)

$$\begin{aligned} \dot{{d}'}_{1}= & {} \frac{\varGamma }{4}({\tilde{d}}_{0}-{\tilde{d}}_{1}). \end{aligned}$$

(44)

Using the initial condition $({c'}_{0}(0),{c'}_{1}(0),d'_{0}(0),d'_{1}(0)) = (1/2,0,0,-1/2)$ associated with $| {\tilde{\varPsi }}_{\text {f}} \rangle ,$ we obtain for $\varGamma \tau \gg 1$:

$$c'_{0,1}(\tau )= -c'_{0,1}(\tau ) \simeq \frac{1}{2\sqrt{2}},$$

(45)

corresponding to state:

$$\begin{aligned} | {\tilde{\varPsi }}_{\text {bw}}(\tau ) \rangle\simeq & {} \frac{1}{\sqrt{2}}\left( \sum _j\left[ \frac{ \phi _{0}(\omega _{j})-\phi _{0}(\omega _{j}-\omega _{\text {m}})}{2}| 0 \rangle _{\text {m}}\right. \right. \\&\left. \quad + \frac{ \phi _{0}(\omega _{j}+\omega _{\text {m}})-\phi _{0}(\omega _{j})}{2}| 1 \rangle _{\text {m}}\right] a_{I,j}^{\dagger }| 0 \rangle _{\text {ph}} \\&\left. \quad -| II \rangle _{\text {ph}}| \text {in} \rangle _{\text {m}}\right) | 0 \rangle _{\text {b}}. \end{aligned}$$

(46)

Now, the amplitude present in the arm I is non zero due to the discrepancy between wavefunctions $\phi _{0}(\omega _{j}\pm \omega _{\text {m}})$ and $\phi _{0}(\omega _{j}),$ which vanishes in the limit of large initial photon frequency variance $\varDelta \omega \gg \omega _{\text {m}}.$ Specifically we have:

$$\begin{aligned} \vert \phi _{0}(\omega _{j})-\phi _{0}(\omega _{j}-\omega _{\text {m}})\vert\simeq & {} \vert \phi _{0}(\omega _{j})-\phi _{0}(\omega _{j}+\omega _{\text {m}})\vert \\\lesssim & {} \frac{\omega _{\text {m}}}{\varDelta \omega }. \end{aligned}$$

(47)