1 Introduction

Fluid-lubricated bearings typically utilise a thin fluid film to maintain a clearance between rotating and stationary components when an axial load is imposed. Increasingly industrial applications of bearings are characterised by high operating speeds, requiring low frictional losses and smaller clearances. Associated film lubrication technology is designed to enable further improvements in bearing efficiency. In this high-speed and small-clearance scenario, comprehensive and accurate predictions of variation in the face clearance are needed, especially when the bearing experiences a range of external loading and disturbances. Quantifying the possibility of contact between the bearing faces is essential.

The dynamics of an air bearing slider, which employs a thin lubricating air film to separate two non-parallel moving plates, has been studied in [1] when the bearing has relative normal motion between the two plates. The interaction of a compressible gas flow with a movable rigid surface was presented, together with linear stability analysis, showing separation of the plates can be maintained. Analytical methods were used in [2] to study the dynamics and stability of tapered air bearing sliders, providing insight into the slider behaviour.

Taylor and Saffman [3] performed an early theoretical study examining a coaxial parallel rotor and stator separated by a thin air film, experiencing normal motion. A model was derived from the compressible Navier–Stokes equations for negligible rotational inertia effects and small amplitude disturbances. For detailed predictions of the bearing dynamics, a coupled bearing model in which the fluid flow is coupled to the bearing structure is required, such that the air film is an integrated component of the bearing [4]. Etison [5] examined a coupled fluid-lubricated device in three dimensions, identifying hydrodynamic and hydrostatic components of the air film pressure; the hydrostatic component includes the squeeze film pressure. Results indicate that the squeeze film behaviour has a significant contribution to the dynamics and can potentially maintain the air film alone. For highly vibrating operational environments, Salbu [6] examined the effect of significant disturbances in the axial direction through theoretical analysis and experimental investigations. Describing the rotor–stator clearance by an oscillatory motion gives predictions of increasing pressure and force in the air film as the amplitude of axial oscillations increases.

The bearing gap dynamics in a coupled high-speed air-lubricated bearing with parallel faces were studied by Garratt et al. [7]. In this case, the axial displacement of one face has periodic axial oscillations of smaller amplitude than the equilibrium film thickness, and the other face moves axially in response to the film dynamics. Bailey et al. [8] considered a similar bearing configuration with the inclusion of a coned rotor and incompressible flow. In this case, an analytical solution of the corresponding Reynolds equation can be found, leading to an explicit analytical expression for the fluid force. The coupled bearing problem then reduces to a second-order non-autonomous ordinary differential equation for the bearing gap. For compressible flow, this direct approach is not feasible due to the nonlinearity of the resulting Reynolds equation. The effect of the rotor undergoing prescribed axial oscillations with amplitude larger than the equilibrium film thickness was examined. Results indicate that the fluid film can become very small, possibly invalidating the classical no-slip velocity condition. Comparison of a CFD model of an air-riding seal with experimental studies by Sayma et al. [9] identified that steady-state flow solutions could not be obtained for typical gaps of under 10 \(\mu \)m indicating more analysis is required at this smaller scale to comprehend the corresponding seal dynamics.

The reduced scale of micro- and nanofluidics devices results in the fluid flow being characterised by the confined fluid at micro- and nanoscales, where surface effects begin to dominate over volume-related phenomena. Mathematical models of thin gas flow regimes are usually classified by the Knudsen number \(Kn=l/{\hat{h}}_0\), where l is the mean free path (for air at atmospheric conditions \(l =68\) nm) and \({\hat{h}}_0\) is the characteristic film thickness. Knudsen numbers in the range \(10^{-3}\le Kn \le 10^{-1}\), represent flow at micro- and nano-scales, where a continuum flow model with slip boundary condition is usually employed. The existence of velocity slip was first predicted by Navier [10], who proposed a constant slip model with a linear relationship between the fluid–wall velocity difference and the tangential shear rate, i.e. the velocity slip is proportional to the derivatives of the surface fluid velocity, with the slip length as the proportionality constant (a first-order model). Using Maxwell’s [11] classical theory, the slip coefficient is taken as proportional to \((2-f)/f\) and is usually of the order of the mean free path; f is the momentum accommodation coefficient.

Use of a slip flow condition has been previously incorporated into models of various bearing geometries. A gas-lubricated inclined plane slider bearing has been studied in the slip flow regime using a first-order slip model [12], second-order slip model [13] and modified second-order slip model incorporating additional physical considerations, referred to as a 1.5 slip model [14]. For each case, the corresponding Reynolds equation for compressible flow was developed and analytical results were obtained.

A non-axisymmetric thrust bearing with slip flow and foil pads on the rotor face is examined by Park et al. [15], where the gas flow modelled by a classical Reynolds equation is coupled to the bearing structure. Bearing dynamic predictions are studied for small amplitude rotor displacement using perturbation analysis in the case of a no-slip and slip condition imposed on the bearing faces. A slip condition results in a reduced hydrodynamic pressure and thus load carrying capacity when compared with a no-slip condition, as well as decreased stiffness and damping coefficients in the case of axial perturbations. Incorporating a slip boundary condition in the analysis of a coupled high-speed fluid-lubricated parallel bearing with small face clearance in the limit of incompressible flow [16] shows that face contact does not formally occur when the rotor undergoes prescribed periodic oscillations but the bearing gap can become very small. An increased lubrication force on the stator can be attained by the use of a coned rotor with stability studies identifying an optimal coning angle [5]. However, detailed analysis of a coned bearing in the slip regime under extreme operating conditions gives predictions of possible face contact [17]. A similar trend is also identified for the case of a coupled high-speed fluid-lubricated bearing in the case of compressible flow with slip boundary conditions under extreme operating conditions [18]. Possible external disturbances imposed on the rotor can cause the rotor to be displaced by magnitudes larger than the initial equilibrium film thickness. Detailed results show a parallel rotor and stator maintain a face clearance, although it can become very small, where as a coned bearing configuration permits contact between the rotor and stator.

For increasingly more compact designs at higher rotational speeds, there exists a requirement for greater predictability of the dynamic behaviour in industrial bearing designs. Sources of uncertainty in a bearing model typically arise from the random axial motion of the rotor due to external excitations. In [16] and [17], the effect of external excitations on the bearing is studied by prescribing the axial motion of the rotor as periodic oscillations and utilising a comprehensive deterministic mathematical model for the bearing dynamics. The probability of bearing face contact is correspondingly examined using the method of derived distributions to incorporate the lack of precise knowledge in the amplitude of rotor oscillations [19]. The probability density function (transforming functions) and cumulative distribution function of the minimum bearing gap are readily determined when the amplitude of rotor oscillations is described by a specified probability distribution function. Utilising the deterministic relationship between the amplitude of rotor oscillations and minimum value of the bearing gap subsequently leads to the evaluation of the probability of contact.

Analysis of dynamical systems and bearing models with uncertainty arising from external excitations use computational methods which are typically based on Monte Carlo techniques [20]. The Monte Carlo method samples directly from the random input parameter and the deterministic model is evaluated for each sample, giving the corresponding output. This robust procedure is able to evaluate complex cases and a large number of uncertain parameters; however, an extensive number of code executions may be needed to generate sufficiently accurate results. To minimise the computational cost and increase efficiency, other computational approaches for uncertainty quantification have been developed; examples include polynomial chaos, Gaussian process emulator and a Quasi-Monte Carlo method, see, e.g. [21,22,23].

The dynamic response and vibration characteristics of two in-line rotor bearing systems are examined by Li et al. [24] to quantify the effects of uncertainty. A model for the rotor system is derived using stochastic modelling based on the polynomial chaos expansion technique for uncertainty in the damping and nonlinear support stiffness. The results obtained are reported to have good agreement with Monte Carlo simulation. Response statistics demonstrate that uncertainty in the nonlinear support stiffness and damping has a significant effect on the predicted dynamic response of the rotor system.

Increasingly environmental and efficiency considerations are leading to the next generation of bearing and sealing technologies having an extremely small gap, resulting in an almost contact design. In this study, we outline a model for a gas-lubricated bearing incorporating a slip boundary condition. The compressible flow model is coupled to the structural dynamics through the axial force of the fluid on the bearing faces. Previous analysis is extended to incorporate operation in a non-ideal environment; external vibrations or disturbances could act to destabilise the bearing which are modelled as a random external force applied to the rotor. In Sect. 2, the coupled governing equations are formulated where a Reynolds equation for compressible flow is derived that retains the effects of centrifugal inertia for high-speed operation and incorporates slip boundary conditions, characterised by a slip length parameter, on the bearing faces. The axial stator and rotor displacements are modelled by spring-mass-damper systems. Of significant importance is the analysis of a random external force imposed on the rotor, modelled as a continuous, stationary, bounded process with finite modes of frequencies in its spectrum. The generality of the proposed random force is potentially transferable to other models of physical phenomena beyond this particular application. To numerically solve the coupled bearing model, the modified Reynolds equation is solved simultaneously with the structural equations via a mapping solver, details of which are given in Sect. 3. The Monte Carlo technique is implemented to determine the cumulative distribution density function of the minimum gap (face clearance) due to the imposed random destabilising external force, and also to find the average of the minimum gap and probability that it reaches a prescribed tolerance. Results are presented in Sect. 4 examining the effect of key model parameters.

2 Mathematical model

A simplified mathematical model is derived for a gas-lubricated bearing with a thin fluid film modelled as compressible flow and a slip boundary condition imposed on the bearing faces. The coaxial, axisymmetric annular rotor and stator can move axially, giving the respective displacement heights as \({\hat{h}}_r\) and \({\hat{h}}_s\). The rotor also has a prescribed rotational speed \(\hat{\varOmega }\) and the bearing has imposed pressures at the inner and outer radius. This configuration is motivated by aerospace applications and similar technology in the literature is referred to as air-riding [7], film-riding [25], oil-free [26] or noncontacting [4].

The governing Navier–Stokes equations and boundary conditions for the gas flow in the bearing are expressed in dimensionless variables by taking a typical bearing radius \({\hat{r}}_0\) and film thickness \({\hat{h}}_0\). The characteristic rotor velocity is taken as \(\hat{\varOmega } {\hat{r}}\), typical air density is taken to be \({\hat{\rho }}_0\) and time is scaled by \({\hat{T}}\) defined by the time scale of an imposed force. The dimensionless velocities are defined as \({\hat{u}}/{\hat{U}}\), \({\hat{v}}/(\hat{\varOmega } {\hat{r}}_0)\) and \({\hat{w}}/({\hat{h}}_0{\hat{T}}^{-1})\), where \(({\hat{u}},{\hat{v}},{\hat{w}})\) are the dimensional radial, azimuthal and axial velocities, respectively. The dimensionless radius and height are given by \(r={\hat{r}}/{\hat{r}}_0\) and \(z=\hat{z}/{\hat{h}}_0\), respectively. The dimensionless density is \(\rho ={\hat{\rho }}/{\hat{\rho }}_0\) and dimensionless slip length is \(l_s=\hat{l_s}/{\hat{h}}_0\).

Fig. 1
figure 1

Geometry and notation of a nondimensional parallel axisymmetric fluid-lubricated bearing

Full size image
Fig. 2
figure 2

Geometry and notation of a nondimensional axisymmetric fluid-lubricated bearing with a negatively coned rotor; in contrast a positively coned rotor has angle below the r axis

Full size image

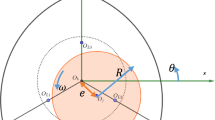
The bearing geometry for parallel faces is shown in Fig. 1 in the dimensionless coordinate system \((r,\theta ,z)\); corresponding geometry for a coned rotor is given in Fig. 2. The coning angle \(\beta \) is assumed small, such that \(\sin \hat{\beta } = O(\delta _0)\) and \(\cos \hat{\beta } = 1 + O(\delta _0)\). Correspondingly, a scaling \(\hat{\beta } = \beta \delta _0\) with \(\beta = O(1)\) gives consistency with the lubrication condition such that \(\partial h_r/\partial r = - \beta \). Figure 3 shows a cross sectional view of a negatively coned bearing (NCB) and positively coned bearing (PCB). The dimensionless coned rotor and plane stator heights are given by \(h_R(r,t;\beta )\) and \(h_s(t)\), respectively, and the axisymmetric rotor–stator clearance is defined by \(h(r,t;\beta )=h_s(t)-h_R(r,t;\beta )\), with rotor height

$$\begin{aligned} h_R(r,t;\beta )=h_r(t)-(r-1)\beta \,\,\,\,\,\,\,\, \text {for} \,\,\,\,\,\,\,\, \beta \le 0,\nonumber \\ h_R(r,t;\beta )=h_r(t)-(r-a)\beta \,\,\,\,\,\,\,\, \text {for} \,\,\,\,\,\,\,\, \beta >0, \end{aligned}$$
(1)

as shown in Fig. 3; \(h_r(t)\) is defined at the outer radius for a NCB and inner radius for a PCB.

The inner radius is rescaled to \(a={\hat{r}}_I/{\hat{r}}_O\) and the outer radius to 1, with corresponding dimensionless pressure boundary conditions

$$\begin{aligned} p=p_I \,\,\,\, \text {at} \,\,\,\,\,r=a, \,\,\,\,\,\,\,\,\,\, \text {and}\,\,\,\,\,\,\,\,\,\, p=p_O \,\,\,\,\, \text {at} \,\,\,\,\, r=1. \end{aligned}$$
(2)

This study considers explicitly the coning angle arising from deformation of the rotor due to over pressurisation of the bearing, resulting in a NCB having external pressurisation \((p_I<p_O)\) and a PCB having internal pressurisation \((p_I>p_O)\). In both cases, this configuration results in a pressure gradient corresponding to a diverging channel.

Fig. 3
figure 3

Cross sectional notation for a bearing with a negative (\(\beta \le 0\)) and b positive (\(\beta > 0\)) coning angle

Full size image

The rotor experiences an external axial force N(t), which is assumed to be axisymmetric and imposed at \(r=a\). It is taken to be a random process, which represents external excitations on the bearing that could act to destabilise the bearing operation. For the case of non-axisymmetric forcing, for example, point loading, the bearing faces may become misaligned and experience tilt and/or swash. In turn, this may lead to coning angle instabilties over time. A dynamic analysis for a noncontacting face seal with coned faces has been examined in three dimensions under the assumption of assembly face misalignment and rotor axial run-out. Optimal conditions to minimise face contact and maximise the stability are addressed in [27,28,29].

A key quantity in the bearing dynamics is the time-dependent minimum face clearance (MFC), defined by the variable \(g(t)=h_s(t)-h_r(t)\), evaluated at the outer radius for a NCB and inner radius for a PCB; for a parallel bearing \(g(t)=h(t)\). If the MFC always remains positive, i.e. \(g>0\), there is no bearing face contact and a fluid film is maintained.

2.1 Air flow model

The air flow model is derived from the compressible Navier–Stokes momentum equations and conservation of mass equation for a compressible flow in axisymmetric coordinates; the flow is assumed to be an isothermal ideal gas. Thermal effects in similar configurations have been studied in the absence of external forcing by numerous authors, for example see [30, 31], suggesting thermal deformation of the faces is more significant than viscous heating. A study by Minikes and Bucher [32] concluded that temperature variations were less than five per-cent of the ambient temperature and consequently the flow could be an isothermal process. Correspondingly, the thermal effects are neglected in the paper as they are secondary to the effects of the dynamic motion.

Under the above approximation the radial and azimuthal Reynolds numbers and the Reynolds number ratio \({Re}^*\) are given respectively as

$$\begin{aligned} Re_U = \frac{{\hat{U}}{\hat{h}}_0}{\nu }, \,\,\,\,\,\,\,\, Re_\varOmega = \frac{{{\hat{r}}_0}^2\hat{\varOmega }}{\nu } \,\,\,\,\,\,\,\, \text {and}\,\,\,\,\,\,\,\, {Re^*} = \frac{\hat{\varOmega } {{\hat{r}}_0}}{{\hat{U}}}{\delta _0}^{-1}, \end{aligned}$$
(3)

where \(\nu =\mu /{\hat{\rho }}_0\) is the kinematic viscosity. The aspect ratio \(\delta _0={\hat{h}}_0/{\hat{r}}_0\) is small for thin film bearings \(\delta _0 \ll 1\), justifying the use of the lubrication approximation. The pressure is scaled as \(P=\mu {\hat{r}}_0{\hat{U}}/{\hat{h}}_0^2\) to ensure that the pressure gradient in the radial direction is retained at leading order and the Froude number Fr is defined as \(Fr={\hat{U}}({\tilde{g}}{\hat{h}}_0)^{-1/2}\), where \(\widetilde{g}\) denotes the acceleration due to gravity and parametrises the importance of gravitational effects relative to the radial flow. Gravity is neglected because taking the Froude number of O(1), ensuring consistency with lubrication theory, leads to \(Re_U \delta _0Fr^{-2}\ll 1\). Classical lubrication theory neglects inertia when the reduced Reynolds number \(Re_U \delta _0\ll 1\); however, in the case of high-speed bearing operation, an additional term corresponding to the ratio of the Reynolds numbers \(Re^*\) must be considered, which is not always negligible. A measure of the importance of the viscous time scale is given by \(\kappa ={{\hat{h}}_0}^2/\nu {\hat{T}}\), where \(\kappa =O(1)\) gives the time scale of the order of the time it takes viscosity effects to diffuse over the characteristic film thickness. Thus giving the acceleration term of the same order as the viscous term. In the current study, the time scale is taken to be of \(O({\hat{h}}_0{\hat{r}}_0/\nu )\), resulting in \(\kappa =O(\delta _0)\), justifying a quasi-static approximation of the momentum equations.

Applying a lubrication condition and the given assumptions to the compressible Navier–Stokes momentum equations, results in the leading-order momentum equations

$$\begin{aligned} -\lambda \rho \frac{v^2}{r} = -\frac{\partial p}{\partial r}+\frac{\partial ^2 u}{\partial z^2}, \quad 0 = \frac{\partial ^2 v}{\partial z^2}, \quad 0 = \frac{\partial p}{\partial z}. \end{aligned}$$
(4)

A speed parameter \(\lambda =Re_U{\delta _0} {Re^*}^2= {{\hat{r}}_0} {{\hat{h}}_0}^2 \hat{\varOmega }^2 /(\nu {\hat{U}})\) characterises effects of inertia due to rotation. If \(\lambda =0\), the standard lubrication equations for compressible flow in axisymmetric cylindrical coordinates are recovered.

Similarly, the conservation of mass equation and equation of state become

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \frac{1}{\sigma r}\frac{\partial }{\partial r}(r\rho u) + \frac{\partial }{\partial z}(\rho w)=0 \quad \text {and} \quad P=K_s\rho , \end{aligned}$$
(5)

where \(\sigma =\kappa / Re_U \delta _0={\hat{r}}_0/{\hat{U}}{\hat{T}}\). The dimensionless ideal gas constant in (5) is given by \(K_s=R\tau {\hat{h}}_0^2/\mu {\hat{r}}_0 {\hat{U}} M\), which relates the pressure field to the density field, where R is the gas constant and M is the molar mass.

A first-order Navier formulation slip model is exploited, as used in Bailey et al. [16], where a slip velocity is introduced that is proportional to the tangential component of the surface traction. The velocity boundary conditions consist of components of the fluid which are continuous across the fluid–solid boundary with a modification due to slip flow induced by the wall shear, together with a no flux condition. Thus the dimensionless velocity boundary conditions, to leading order, are taken as

$$\begin{aligned}&u=l_s\frac{\partial u}{\partial z},\,\,\,\,\,\,\,\,\,\,\,\, v=r +l_s\frac{\partial v}{\partial z},\,\,\,\,\, w=\frac{\partial h_r}{\partial t}- \frac{Re_U\delta _0}{\kappa }u\beta \,\,\,\,\, \text {at} \,\,\,\,\, z=h_r, \nonumber \\&u=-\,l_s\frac{\partial u}{\partial z}, \,\,\,\,\, v=-\,l_s\frac{\partial v}{\partial z}, \,\,\,\,\,\,\,\,\,\,\,\,\, w=\frac{d h_s}{d t} \quad \text {at} \,\,\,\,\, z=h_s. \end{aligned}$$
(6)

The fluid velocity components tangential to the wall in (6) are proportional to the relevant wall shear stress where the proportionality constant \(l_s\), denotes a dimensionless slip length. The limit \(l_s=0\) corresponds to no-slip conditions. A derivation of the slip velocity conditions is given in Bailey et al. [17].

The air flow velocities are readily determined from the leading order Navier–Stokes equations (4). Integrating the conservation of mass equation (5) between the rotor and stator, applying the Leibniz integral rule and the velocity boundary conditions (6), gives the modified nonlinear Reynolds equation for compressible flow as

$$\begin{aligned}&\frac{\partial }{\partial t}(ph) - \frac{1}{12 \sigma r}\frac{\partial }{\partial r}\left( pr\frac{\partial p}{\partial r}h^2(h+6l_s)\right) + \frac{\lambda }{12 K_s \sigma r}\frac{\partial }{\partial r}\left( p^2r^2\frac{h^2\left( \frac{3}{10}h^3+3h^2l_s+7h{l_s}^2+6{l_s}^3\right) }{(h+2l_s)^2}\right) =0. \end{aligned}$$
(7)

The modified Reynolds equation expresses the relationship between the film pressure and rotor–stator clearance h, subsequently yielding the flow characteristics when solved. Dependence on the coning angle is given implicitly in the rotor–stator clearance h. Taking \(\lambda =0\) results in the centrifugal inertia effects being neglected;however, the rotor and stator still experience relative rotational motion due to the velocity boundary conditions.

2.2 Structural dynamics

The axial displacements of the stator and rotor are modelled using a standard spring-mass-damper model incorporating the bearing pressure variation and an external random, time-dependent force imposed on the rotor N(t). In dimensionless form, the stator equation is

$$\begin{aligned} \frac{\mathrm{{d}}^2h_s}{\mathrm{{d}} t^2}+D_{a}\frac{\mathrm{{d}} h_s}{\mathrm{{d}} t}+K_{z}(h_s-1)=\alpha F(t), \end{aligned}$$
(8)

and the rotor equation is either

$$\begin{aligned} \frac{\mathrm{{d}}^2h_r}{\mathrm{{d}} t^2}+D_{a}\frac{\mathrm{{d}} h_r}{\mathrm{{d}} t}+K_{z}(h_r+(1-a)\beta )=-\alpha (F(t) - N(t))\,\,\,\,\,\,\,\, \text {for} \,\,\,\,\,\,\,\, \beta \le 0, \end{aligned}$$

or

$$\begin{aligned} \frac{\mathrm{{d}}^2h_r}{\mathrm{{d}} t^2}+D_{a}\frac{\mathrm{{d}} h_r}{\mathrm{{d}} t}+K_{z}h_r=-\alpha (F(t) - N(t)) \quad \text {for} \,\,\,\,\,\,\,\, \beta >0. \end{aligned}$$
(9)

The rotor equations (9) are defined at \(r=a\), resulting in separate equations for cases of a NCB and PCB, to ensure that they have a similar volume of gas in the bearing for a given magnitude of coning angle. In this configuration, a PCB and a NCB have different equilibrium rotor heights at \(r=a\).

The corresponding fluid axial force of the fluid on the bearing faces is given by

$$\begin{aligned} F(t)=2\pi \int ^1_a(p-p_a)r\,\mathrm{{d}}r. \end{aligned}$$
(10)

Here \(p_a=\hat{p}_a/\hat{P}\) is the dimensionless atmospheric pressure, \(\alpha =\nu {\hat{U}}/\hat{m}\sigma ^2\delta _0^3\) is the dimensionless force coupling parameter, \(\hat{m}\) is the mass of a face, \(D_{a}=\hat{D}_{a}/\hat{m}\sigma \) is the dimensionless damping parameter and \(K_{z}=\hat{K}_{z}/\hat{m}\sigma ^2\) is the effective restoring force parameters.

In a physical application, random fluctuations reflect the uncertainty in the precise state of a system. In the present work, the bearing is envisaged as part of a complex dynamical system characterised by a periodic motion of period \({\hat{T}}\); this will be the case for an aero-turbine engine. The system is composed of several rotating parts where the motion of each individual part and its interaction with the surrounding environment induce an external force on the rotor surface of the bearing. As the external force is not known with any precision, it is considered to be a random force. Due to restrictions on the mathematical formulation of the problem as well as physical and operating constraints, the external force is taken to be continuous, stationary, having a bounded amplitude, and a finite number of frequencies in its spectrum. Correspondingly, the random external force is chosen of the form

$$\begin{aligned} N(t)=\sum _{i=1}^nA_i\cos (B_i t+\phi _i), \end{aligned}$$
(11)

and amplitudes \(A_i\) are truncated normal random variables given by

$$\begin{aligned} A_i= {\left\{ \begin{array}{ll} \bar{A}, &{}\text {if}\,\,\,\,\, X_i>\bar{A},\\ X_i, &{}\text {if}\,\,\,\,\, -\bar{A}\le X_i\le \bar{A},\\ -\bar{A},&{} \text {if}\,\,\,\,\, X_i<-\bar{A},\\ \end{array}\right. } \end{aligned}$$
(12)

where \(X_i\) are standard normal random variables; the phases \(\phi _i\) are uniformly distributed random variables on \([0, 2\pi ]\); and the frequencies \(B_i\) are taken as discrete random variables uniformly distributed on the finite set of non-negative integers: \(\{0,1,\ldots ,\bar{B}\}\). The choice of \(\bar{B}\) is motivated by the need for the time scale of the forcing to be comparable or longer than the viscous time scale. The random variables \(X_i\), \(B_i\), \(\phi _i\), \(i=1,\ldots ,n\) are mutually independent.

The form of the random external force N(t) contrasts with Langevin-type equations associated with white noise models that are typically unbounded, discontinuous and aperiodic [33, 34]. Boundedness of the noise and frequency in the current work, together with continuity, is important for a realistic model of an external force in aero-applications. Correspondingly, a realisation of N(t) from (11), determined from a realisation of \(A_i\), \(B_i\), \(\phi _i\), provides a periodic function of time. Noting that \(\phi _i\) is a uniform random variable on \([0,\, 2\pi ]\), then N(t) is a stationary stochastic process [35, 36]. Since \(A_i\) are bounded random variables and n is finite, N(t) is bounded which is a natural requirement for modelling a physical force. The properties of the proposed random force (11), namely that it is continuous, stationary, boundedness in physical space and has a finite number of frequencies in its spectrum, is potentially transferable to other models; the proposed random force may be useful when modelling other physical phenomena which experience random fluctuations.

3 Numerical methods

Consideration of a fully coupled bearing model provides a quantitative study of the interaction between the air film and the rotor–stator structure of fluid-lubricated technology. Investigations into the operational requirements for dynamic bearing behaviour are undertaken in the presence of an external force subject to uncertainties on the rotor. To numerically solve the coupled bearing model requires the modified Reynolds equation (7) to be simulated simultaneously with the structural equations (8)–(9). Equations are derived for a NCB, and similar methodolgy can be followed for those for a PCB, see Bailey et al. [18]. Substituting the MFC \(g(t)=h_s(t)-h_r(t)\) into the modified Reynolds equation (7) gives

$$\begin{aligned}&\frac{\partial }{\partial t}(p(g+(r-1)\beta )) - \frac{1}{12 \sigma r}\frac{\partial }{\partial r}\left( pr\frac{\partial p}{\partial r}(g+(r-1)\beta )^2(g+(r-1)\beta +6l_s)\right) \nonumber \\&\quad + \frac{\lambda }{12 K_s \sigma r}\frac{\partial }{\partial r}\left( p^2r^2(g+(r-1)\beta )^2\frac{\left( \frac{3}{10}(g+(r-1)\beta )^3+3(g+(r-1)\beta )^2l_s\right) }{(g+(r-1)\beta +2l_s)^2}\right. \nonumber \\&\quad +\left. \frac{\left( 7(g+(r-1)\beta ){l_s}^2+6{l_s}^3\right) }{(g+(r-1)\beta +2l_s)^2}\right) =0, \end{aligned}$$
(13)

for a NCB. The equation for a parallel bearing is obtained from (13) by taking \(\beta =0\).

Re-writing the stator equation (8) in terms of the MFC gives the system of structural equations for a NCB or parallel bearing as

$$\begin{aligned}&\frac{\mathrm{{d}}^2g}{\mathrm{{d}} t^2} + D_a\frac{\mathrm{{d}}g}{\mathrm{{d}} t} + K_z(g-1 - (1-a)\beta ) - 2\alpha F(t) + \alpha N(t)=0,\nonumber \\&\frac{\mathrm{{d}}^2h_r}{\mathrm{{d}} t^2}+D_a\frac{\mathrm{{d}} h_r}{\mathrm{{d}} t}+K_z(h_r-(1-a)\beta )+\alpha (F(t) - N(t)) = 0. \end{aligned}$$
(14)

To couple numerically the structural and fluid dynamics, the Reynolds equation is discretised in the spatial variable and approximated by a second-order central finite difference scheme.

Solutions to the coupled system, Reynolds equation (13) and structural equations (14), are denoted by the vector \(\mathbf {g}(g(t),h_r(t),Z(t),Y(t),p_i(t))\), where \(p_i\) denotes the pressure at radial points \(r_i\); \(a\le r_i \le 1\), with given initial conditions:

$$\begin{aligned}&g(t_0)=g_0,\,\,\,\,\,\,\,\,\,\, h_r(t_0)=h_{r0},\,\,\,\,\,\,\,\,\,\, Z(t_0)=Z_0,\,\,\,\,\,\,\,\,\,\, Y(t_0)=Y_0,\,\,\,\,\,\,\,\,\,\, p_i(t_0)=\frac{p_O(r_i-a)+p_I(1-r_i)}{1-a}. \end{aligned}$$
(15)

In this way, the problem reduces to the following system of five first-order random ordinary differential equations. For a NCB, the set of equations is given by

$$\begin{aligned} \frac{\text {d}g}{\text {d}t}= & {} Z,\nonumber \\ \frac{\text {d}h_r}{\text {d}t}= & {} Y,\nonumber \\ \frac{\text {d}Z}{\text {d} t}= & {} -D_aZ-K_z(g-1-(1-a)\beta ) +2\alpha F -\alpha N(t),\nonumber \\ \frac{\text {d}Y}{\text {d} t}= & {} -D_aY-K_z(h_r-(1-a)\beta )-\alpha F +\alpha N(t),\nonumber \\ \frac{\text {d}p_i}{\text {d} t}= & {} - \frac{p_iZ}{(g+(r_i-1)\beta )} + \frac{p_ir_i(p_{i+1}-p_{i-1})}{24\sigma \delta r}(3\beta (g+(r_i-1)\beta +4l_s))\nonumber \\&+\, \frac{(g+(r_i-1)\beta )(g+(r_i-1)\beta +6l_s)}{12\sigma }\left( \frac{p_{i+1}-p_{i-1}}{4r_i\delta r}+\frac{{p_{i+1}}^2-2{p_i}^2+{p_{i-1}}^2}{2{\delta r}^2}\right) \nonumber \\&-\,\frac{\lambda }{12\sigma K_s}\frac{(g+(r_i-1)\beta )}{(g+(r_i-1)\beta +2l_s)^2}\left( \frac{3}{10}(g+(r_i-1)\beta )^3+3(g+(r_i-1)\beta )^2l_s\right. \nonumber \\&\left. +\,7(g+(r_i-1)\beta ){l_s}^2+6{l_s}^3\right) \left( \frac{{p_{i+1}}^2{r_{i+1}}^2-2{p_i}^2{r_i}^2+{p_{i-1}}^2{r_{i-1}}^2}{2r_i{\delta r}^2}\right) \nonumber \\&-\frac{\lambda }{12\sigma K_s}\frac{{p_i}^2{r_i}^2\beta }{(g+(r_i-1)\beta +2l_s)^3}\left( \frac{9}{10}(g+(r_i-1)\beta )^4+9(g+(r_i-1)\beta )^3l_s\right. \nonumber \\&\left. +\,31(g+(r_i-1)\beta )^2{l_s}^2+42(g+(r_i-1)\beta ){l_s}^3+24{l_s}^4\right) . \end{aligned}$$
(16)

The Reynolds equation is discretised in the spatial variable and approximated by a second-order central finite difference scheme for \(i=2:\xi -1\), where \(\xi \) is the number of radial points used in the finite difference approximation of equation (13). The boundary conditions for the pressure are given by \(p_1=p_I\) and \(p_\xi =p_O\). The force of the fluid on the faces is denoted by \(F=2\pi \left( \sum _{i=1}^{\xi }w_i(p_i-p_a)r_i\right) \), where \(w_i\) is a weighting function. The set of equations (13) are solved using a stiff ordinary differential equation solver, namely a variable-step, variable-order solver based on the numerical differentiation formulas of orders 1 to 5.

For every realisation of the random force (11), the rotor experiences a periodic force which has a period of \(T=2\pi \). Periodic solutions of the system of equations (16), with fixed \(A_i\), \(B_i\), \(\phi _i\) in (11), are sought; the solver used only converges to periodic solutions. Therefore, a \(\mathfrak {R}^2\rightarrow \mathfrak {R}^2\) map is formulated, advancing an initial condition \(\mathbf {g}_0\) at time \(t_0\) by the time \(T=2\pi \), defining a stroboscopic map \(\Phi (T;\mathbf {g}_0,t_0)\) which integrates the system of equations (16) forward through one period of the forcing. A variable-order solver based on the numerical differentiation formulas is implemented due to the equations becoming locally stiff when the face clearance becomes very small. Periodic solutions are identified via the fixed points of the stroboscopic map \(\mathbf {g}(t)=\mathbf {g}(t+T)\) and found iteratively, corresponding to the condition

$$\begin{aligned} \mathbf {g}(T)-\mathbf {g}(t_0)=\mathbf {\Phi }(T;\mathbf {g_0},t_0)-\mathbf {g_0}=\mathbf {G} (\mathbf {\Phi }(T;\mathbf {g_0},{t_0}),\mathbf {g_0})=0, \end{aligned}$$
(17)

giving periodic solutions \(\mathbf {g}(g(t),h_r(t),Z(t),Y(t),p_i(t))\).

Due to the nonlinear character of the system of equations, an iterative Newton’s method is used to find solutions numerically, given an initial guess value \({\tilde{\mathbf {g}}}_0\). Successively improved iterates of the initial guess \(\mathbf {g}_0\) are computed by the numerical iterative scheme

$$\begin{aligned} \mathbf {g_0}_{n+1} = \tilde{\mathbf {g_0}}_n-J(T)^{-1}(\mathbf {g}(T)-\tilde{\mathbf {g_0}}_n), \end{aligned}$$
(18)

with the Jacobian matrix

$$\begin{aligned} J(T)= & {} \frac{\partial \mathbf {G}(\mathbf {{\Phi }},\mathbf {g_0})}{\partial \mathbf {g_0}}\nonumber \\= & {} { \begin{bmatrix} \frac{\partial g(T)}{\partial g_0}-1&\frac{\partial g(T)}{\partial h_{r0}}&\frac{\partial g(T)}{\partial z_0}&\frac{\partial g(T)}{\partial Y_0}&\frac{\partial g(T)}{\partial p_{10}}&\cdots&\frac{\partial g(T)}{\partial p_{\xi 0}} \\ \frac{\partial h_r(T)}{\partial g_0}&\frac{\partial h_r(T)}{\partial h_{r0}}-1&\frac{\partial h_r(T)}{\partial z_0}&\frac{\partial h_r(T)}{\partial Y_0}&\frac{\partial h_r(T)}{\partial p_{10}}&\cdots&\frac{\partial h_r(T)}{\partial p_{\xi 0}} \\ \frac{\partial Z(T)}{\partial g_0}&\frac{\partial Z(T)}{\partial h_{r0}}&\frac{\partial Z(T)}{\partial z_0}-1&\frac{\partial Z(T)}{\partial Y_0}&\frac{\partial Z(T)}{\partial p_{10}}&\cdots&\frac{\partial Z(T)}{\partial p_{\xi 0}} \\ \frac{\partial Y(T)}{\partial g_0}&\frac{\partial Y(T)}{\partial h_{r0}}&\frac{\partial Y(T)}{\partial z_0}&\frac{\partial Y(T)}{\partial Y_0}-1&\frac{\partial Y(T)}{\partial p_{10}}&\cdots&\frac{\partial Y(T)}{\partial p_{\xi 0}} \\ \frac{\partial p_1(T)}{\partial g_0}&\frac{\partial p_1(T)}{\partial h_{r0}}&\frac{\partial p_1(T)}{\partial z_0}&\frac{\partial p_1(T)}{\partial Y_0}&\frac{\partial p_1(T)}{\partial p_{10}} - I&\cdots&\frac{\partial p_1(T)}{\partial p_{\xi 0}} \\ \vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots \\ \frac{\partial p_\xi (T)}{\partial g_0}&\frac{\partial p_\xi (T)}{\partial h_{r0}}&\frac{\partial p_\xi (T)}{\partial z_0}&\frac{\partial p_\xi (T)}{\partial Y_0}&\frac{\partial p_1(T)}{\partial p_{10}}&\cdots&\frac{\partial p_\xi (T)}{\partial p_{\xi 0}} - I \\\end{bmatrix}.\,\,\,\,\,\,\,\,} \end{aligned}$$
(19)

The elements of the Jacobian matrix J(T) are found by solving similar systems to the auxiliary system of equations (16), but which are the derivative with respect to each of the initial guess value \(\tilde{\mathbf {g}}_0\); corresponding initial conditions are used.

An alternative method, as the modified Reynolds equation (13) does not depend explicitly on the rotor height \(h_r\), is to solve directly for the pressure and face clearance only and find the rotor height in post processing using F(t) and N(t). This will eliminate the second and fourth equations in (16) and reduce the Jacobian (19) by removing the second and fourth rows and columns. However, if the number of radial points \(\xi \) is large, the reduction will be marginal.

The stroboscopic map is combined with the Monte Carlo technique, where a large number of independent random realisations of the stroboscopic map are computed, each with a randomly generated external force imposed on the rotor.

Initially, the stroboscopic map is used to obtain the approximation \(\bar{g}_\mathrm{{min}}\) of the minimum face clearance \(g_\mathrm{{min}}\) as

$$\begin{aligned} g_\mathrm{{min}}=\lim _{t\in [0,T]} g(t). \end{aligned}$$

Then the approximate average of \(g_\mathrm{{min}}\) can be computed as

$$\begin{aligned} E[g_\mathrm{{min}}]\approx E[\bar{g}_\mathrm{{min}}]\approx \hat{g}_\mathrm{{min}}:=\frac{1}{M}\sum ^M_{m=1}{\bar{g}_\mathrm{{min}}}^{(m)}, \end{aligned}$$
(20)

where \(\hat{g}_\mathrm{{min}}\) is the approximate average of \(\bar{g}_\mathrm{{min}}\) and \(\bar{g}_\mathrm{{min}}^{(m)}\) is the value of \(\bar{g}_\mathrm{{min}}\) for independent realisation m; \(m=1,\ldots ,M\). The Monte Carlo error is

$$\begin{aligned} MC_{\mathrm{{err}}_{g_\mathrm{{min}}}}=2\sqrt{var (\bar{g}_\mathrm{{min}})}/\sqrt{M}, \end{aligned}$$
(21)

where \(var(\bar{g}_\mathrm{{min}})\) is estimated as

$$\begin{aligned} var (\bar{g}_\mathrm{{min}})\simeq {\hat{\sigma }}^2 := \frac{1}{M} \sum _{m=1}^M\left[ \bar{g}_\mathrm{{min}}^{(m)}\right] ^2 - \left[ \hat{g}_\mathrm{{min}}\right] ^2, \end{aligned}$$
(22)

and

$$\begin{aligned} E[\bar{g}_\mathrm{{min}}] \in \left( \hat{g}_\mathrm{{min}}-MC_\mathrm{{err}},\hat{g}_\mathrm{{min}}+MC_\mathrm{{err}}\right) \end{aligned}$$
(23)

with a probability of \(95\%\) (confidence interval). To achieve a sufficiently accurate result, the Monte Carlo error was made sufficiently small through choosing an appropriately large number M of independent realisations. We note that the estimate \(\hat{g}_\mathrm{{min}}\) has bias \(E[g_\mathrm{{min}}]-E[\bar{g}_\mathrm{{min}}]\), corresponding to the error of the numerical approximation \(\bar{g}(t)\) of the stroboscopic map g(t). The numerical solution was compared to an analytical asymptotic solution in the case of small face clearance in Bailey et al. [8]. Results showed the proposed numerical solution has negligible error of the minimum face clearance compared to the asymptotic solution, indicating that the bias of the estimate \(\hat{g}_\mathrm{{min}}\) can be considered to be negligible. An estimate for the variance of \(g_\mathrm{{min}}\) is computed as in (22), and its Monte Carlo error is evaluated as

$$\begin{aligned} MC_{\mathrm{{err}}_{\sigma ^2}}\simeq \frac{2}{\sqrt{M}}\left( \frac{1}{M}\sum ^M_{m=1}\left[ \bar{g}^{(m)}_\mathrm{{min}}\right] ^4-\left[ \hat{\sigma }^2\right] ^2\right) ^\frac{1}{2}. \end{aligned}$$
(24)

4 Results and discussion

A coupled gas bearing is examined to investigate the effects of key parameters of the bearing dynamics and to identify possible face contact corresponding to a generic aero-engine industrial application. The bearing configuration is taken to be a narrow bearing \(a=0.8\) with \(\sigma =0.821\) and ambient pressure imposed at the outer radius \(p_O=p_a=1\). Initially ambient pressure is considered at the inner radius \(p_I=1\), the bearing faces taken to be parallel \(\beta =0\) and the external force (11) has parameters \(n=20\), \(\bar{B}=10\), and \(\bar{A}=20\); the effect of these parameters on potential face contact is examined. The speed parameter is considered to be \(\lambda =0.0029\), dimensionless slip length to be \(l_s=0.1\) and the ideal gas constant as \(K_s=1\). The structural parameters are given by \(K_z=12.2\), \(D_a=1.5\) and the force coupling parameter by \(\alpha =1.22\).

These parameter values refer to a bearing with characteristic radius \({\hat{r}}_0=0.01\) m, rotor–stator clearance \({\hat{h}}_0=0.3 \times 10^{-4}\)m and typical pressure \(\hat{P}=5 \times 10^3\) Pa. The bearing faces have mass 1 Kg and the structural stiffness is given as \(\hat{K}_z=5 \times 10^5\) Nm\(^{-1}\) and the damping as \(\hat{D}_a=300\) Nsm\(^{-1}\). The fluid properties are given by \({\hat{\rho }}_0=1.2922\) Kgm\(^{-1}\), \(\mu =2.026 \times 10^{-5}\) Kgm\(^{-1}\)s\(^{-1}\) and the rotational speed of the rotor is taken to be 6000 rpm.

Fig. 4
figure 4

Pressure in the fluid film, fluid force on bearing faces, stator and rotor height, face clearance and external force imposed on the rotor for two particular realisations of the random force N(t) in the case of a parallel bearing for a typical realisation and b extreme realisation with small face clearance; \(n=20\), \(\bar{A}= 20\), \(\beta =0\) and \(p_I=1\)

Full size image

As examples, two different realisations of the bearing dynamics are given in Fig. 4 showing the pressure in the fluid film, force of the fluid on the bearing faces, the stator and rotor heights, face clearance and external force imposed on the rotor. It is noted that the realisation in Fig. 4b is an extreme realisation where the face clearance becomes very small, and a more typical representation of the evolution of the system is given in Fig. 4a. The external axial force on the rotor causes axial displacement of the rotor: however, the stator only has axial displacement if the rotor displacements are sufficiently large such that the face clearance becomes sufficiently small. When the rotor is in close proximity of the stator, resulting in a very small face clearance, as shown in Fig. 4b, there is a peak in the fluid force and pressure of the fluid ensuring the fluid film is maintained through axial displacement of the stator. The stator oscillations decrease over time unless the rotor comes into close proximity again (as in Fig. 4b), where there is another peak in the fluid force and further axial displacement of the stator. The smaller the face clearance becomes, the larger the peaks in the fluid force and pressure in the fluid film become.

Fig. 5
figure 5

Mean and variance of the minimum face clearance \(g_\mathrm{{min}}\) with the corresponding Monte Carlo errors for an increasing number of realisations \(1000\le M\le 15,000\); \(n=20\), \(\bar{A}= 20\), \(\beta =0\) and \(p_I=1\)

Full size image

The mean value and variance of the minimum face clearance are computed for an increasing number of Monte Carlo simulations and are given in Fig. 5 for a parallel bearing together with the corresponding Monte Carlo errors. Increasing the number of Monte Carlo realisations gives converging values for the mean and variance of the minimum face clearance of \(\mu =0.447\pm 0.00340\) and \(\sigma ^2=0.0432\pm 0.000885\). Increasing the number of realisation from \(M=1000\) to \(M=4000\) effectively halves the Monte Carlo error for mean value from \(3.00\%\) to \(1.48\%\). Increasing the number of realisations further to \(M=15,000\) reduces the Monte Carlo error to \(0.760\%\), signifying a balance between the accuracy of the results and the excessive computation requirement that is desirable. For all subsequent cases considered, the number of realisations will be chosen such that the Monte Carlo error is \(\le 2.5\%\) for the mean value of \(g_\mathrm{{min}}\) to limit computation time without a significant loss in accuracy.

Fig. 6
figure 6

Histogram for \(g_\mathrm{{min}}\) corresponding to the Monte Carlo simulation with \(M=15,000\); \(n=20\), \(\bar{A}=20\), \(\beta =0\) and \(P_I=1\)

Full size image

A histogram for \(g_\mathrm{{min}}\) is presented in Fig. 6 for the case of \(M=15,000\) in Fig. 5 showing the frequency distribution. The realisations give a right-skewed distribution due to the dynamics of the bearing when the face clearance becomes very small, i.e. in the limit of contact. The average value of \(g_\mathrm{{min}}\) is \(0.447\,\pm \,0.00340\); however, there is a non-negligible possibility of the face clearance reaching a small prescribed tolerance, with the limiting case of contact \(g_\mathrm{{min}}=0\).

Fig. 7
figure 7

Mean and variance of \(g_\mathrm{{min}}\) with corresponding Monte Carlo errors in the case of the parallel bearing with increasing pressures \(p_I\) at the inner radius; \(n=20\), \(\bar{A}=20\) and \(\beta =0\)

Full size image

Evaluation of the parallel bearing is examined for increasing internal pressure imposed at the inner radius; for \(p_I=1\) an ambient pressure is imposed across the bearing, \(p_I=0.5\) corresponds to external pressurisation and \(p_I=1.5\) to internal pressurisation. The mean and variance of \(g_\mathrm{{min}}\) are given in Fig. 7, together with the corresponding Monte Carlo error, for a parallel bearing with increasing pressure at the inner radius \(p_I\). In general, as the pressure at the inner radius is increased, the average value of \(g_\mathrm{{min}}\) increases. It is noted that the case of \(p_I=1.1\) has a value less than \(p_I=1\), however with the Monte Carlo error this case fits with the overall trend of the mean value of \(g_\mathrm{{min}}\) increasing as the value of \(p_I\) increases. In all cases, the variance of \(g_\mathrm{{min}}\) is small; \(\sigma ^2\) is of the order of \(10^{-2}\).

The corresponding probability of \(g_\mathrm{{min}}\) reaching a prescribed tolerance \(g_\mathrm{{tol}}\) is given in Fig. 8, including the Monte Carlo errors. Of note is that the probability decreases as the prescribed tolerance decreases, with negligible probability of face contact, i.e. \(g_\mathrm{{tol}}\sim 0\). For each prescribed tolerance, increasing the pressure at the inner radius leads to a general trend of the probability of \(g_\mathrm{{min}}\) reaching the value of \(g_\mathrm{{tol}}\) decreasing. There are larger decreases in the probability of \(g_\mathrm{{min}}\) reaching a prescribed tolerance for large values of \(g_\mathrm{{tol}}\).

Fig. 8
figure 8

Probability of \(g_\mathrm{{min}}\) reaching a given tolerance \(g_\mathrm{{tol}}\) in the case of the parallel bearing for increasing values of pressure \(p_I\) at the inner radius; \(n=20\), \(\bar{A}= 20\) and \(\beta =0\)

Full size image
Fig. 9
figure 9

Mean and variance of \(g_\mathrm{{min}}\) with corresponding Monte Carlo errors in the case of the parallel bearing with increasing values for the truncated amplitude of the components of the random force \(\bar{A}\); \(n=20\), \(\beta =0\) and \(p_I=1\)

Full size image
Fig. 10
figure 10

Probability of \(g_\mathrm{{min}}\) reaching a given tolerance \(g_\mathrm{{tol}}\) in the case of the parallel bearing for increasing values for the truncated amplitude of the components of the random force \(\bar{A}\); \(n=20\), \(\beta =0\) and \(p_I=1\)

Full size image

Figure 9 gives the mean and variance of \(g_\mathrm{{min}}\) with the corresponding Monte Carlo errors in the case of increasing values for the truncated amplitude of the components of the random force. Corresponding values of the probability of \(g_\mathrm{{min}}\) reaching a prescribed tolerance of decreasing value \(g_\mathrm{{tol}}\) for increasing \(\bar{A}\) are given in Fig. 10. The bound \(\bar{A}\) of the truncated random variable \(A_i\) models the amplitude of the individual components of the random force N(t); the bound is finite due to the structural limitation of the bearing geometry and its local environment. To test our numerical solution, values \(20\le \bar{A} \le 100\) are examined; the mean value of \(g_\mathrm{{min}}\) is similiar for all cases examined, and the variance has a small value of the order of \(10^{-2}\) in all cases. The probability of \(g_\mathrm{{min}}\) reaching a given tolerance \(g_\mathrm{{tol}}\) remains similiar when the values of \(\bar{A}\) increase, with negligible probability of face contact, i.e. \(g_\mathrm{{tol}}\sim 0\).

Table 1 Mean and variance of \(g_\mathrm{min}\) for a given number of realisations M together with the probability of \(g_\mathrm{min}\) reaching a given tolerance \(g_\mathrm{tol}\) in the case of a parallel bearing with increasing number of frequencies in the forcing term \(10\le n \le 30\); \(\bar{A}=20\), \(\beta =0\) and \(p_I=1\)
Full size table

The mean and variance of \(g_\mathrm{{min}}\) with the corresponding Monte Carlo errors are shown in Table 1 for the case of a parallel bearing with increasing number of frequencies (modes) in the forcing term (11), together with the probability of \(g_\mathrm{{min}}\) reaching a prescribed tolerance \(g_\mathrm{{tol}}\). For an increasing number of frequencies, the number of Monte Carlo realisations required increases, and the mean value of \(g_\mathrm{{min}}\) decreases, while the variance increases. Decreasing the prescribed tolerance causes the probability of \(g_\mathrm{{min}}\) becoming that small to decrease, with negligible probability of \(g_\mathrm{{min}}\) reaching zero. Increasing the number of frequencies in the forcing term leads to an increase in the probability of \(g_\mathrm{{min}}\) reaching the prescribed tolerance. This can be observed as the increasing the number of random models causes the mean value of the minimum gap to significantly decrease with a corresponding increase in the variance.

Table 2 Mean and variance of \(g_\mathrm{{min}}\) for given number of realisations M in the case of a NCB (\(p_I=0.5\)) and PCB (\(p_I=1.5\)); \(n=20\) and \(\bar{A}=20\)
Full size table

Analysis of a coned bearing is undertaken to examine the effects of possible rotor deformation arising due to the possible over pressurisation of the inner radius of the bearing. Correspondingly, a NCB is examined under external pressurisation; \(p_I=0.5\) and a PCB under internal pressurisation; \(p_I=1.5\). Table 2 gives the mean value and variance of \(g_\mathrm{{min}}\) (\(\mu \) and \(\sigma ^2\), respectively) with the corresponding Monte Carlo errors in the case of a NCB and PCB; for comparison, a parallel bearing is examined under the respective pressure boundary conditions. In general, a PCB requires less realisations than a NCB to obtain the required level of accuracy and has larger values for the mean value of \(g_\mathrm{{min}}\) and variance. A NCB has a monotonic decrease in the mean value of \(g_\mathrm{{min}}\) as the magnitude of the coning angle increases, whereas a PCB has a non-monotonic trend. The non-monotonic trend in the case of a PCB may be due to the pressure gradient across the bearing resulting in an internally pressurised bearing as opposed to a NCB being externally pressurised.

Fig. 11
figure 11

Cumulative distribution function of \(g_\mathrm{{min}}\) for a \(\beta =0\) (\(p_I=0.5\)), b \(\beta =0\) (\(p_I=1.5\)) c \(\beta =-0.3\), d \( \beta =0.3\); \(n=20\) and \(\bar{A}=20\)

Full size image
Table 3 Probability of \(g_\mathrm{{min}}\) reaching a prescribed tolerance \(g_\mathrm{{tol}}\) in the case of a NCB (\(p_I=0.5\)) and PCB (\(p_I=1.5\)); \(n=20\) and \(\bar{A}=20\)
Full size table

The cumulative distribution function (CDF) is examined which gives the probability that \(g_\mathrm{{min}}\) is less than or equal to a given value of \(g_\mathrm{{min}}\), i.e. \(F_{g_\mathrm{{min}}}(x)=\text {Prob}(g_\mathrm{{min}} \le x)\). The cases of \(\beta =0\) and \(\mid \beta \mid = 0.3\) for a NCB and PCB are shown in Fig. 11 with \(95\%\) upper and lower confidence bounds; the probability of contact is given by the CDF when \(g_\mathrm{{min}}=0\). The probability that \(g_\mathrm{{min}}\) becomes equal to or less than a prescribed tolerance \(g_\mathrm{{tol}}\) is shown in Table 3; note that the parallel bearing is examined under different pressurisations for comparison. Both scenarios have predictions for a parallel bearing having negligible probability of contact. In contrast, a coned bearing has a non-zero probability of contact for all the cases considered. A NCB has an increase in the probability of \(g_\mathrm{{min}}\) reaching a given tolerance as the magnitude of the coning angle increases. However, in the case of a PCB this situation occurs only for \(g_\mathrm{{tol}}=0.001\) and \(g_\mathrm{{tol}}=0\); there is a non-monotonic trend otherwise. A NCB has a larger probability of \(g_\mathrm{{min}}\) reaching the prescribed tolerance than the corresponding PCB, resulting in a higher probability of contact at the outer radius of the bearing than at the inner radius (see geometry in Fig. 3). The asymmetry between the behaviour of a NCB and PCB is noted; a NCB has a monotonic trend always, whereas a PCB can have a non-monotonic trend as seen in Tables 2 and 3. This type of analysis can be used to identify safe operating conditions or limitations on bearing geometries under operating conditions.

5 Conclusions

A dynamical model for a gas-lubricated bearing with a very small face clearance is derived, which is capable of predicting the bearing dynamics under destabilising operating conditions. A modified compressible Reynolds equation is formulated to model a gas film, which is then coupled to the bearing structure through an axial force of the gas on the bearing faces. The governing compressible Navier–Stokes equations are reduced through using an axisymmetric lubrication approximation, but maintain leading-order effects of centrifugal inertia, relevant for high-speed flows. Modified surface boundary conditions corresponding to a slip length formulation are incorporated, relevant to the case of very small face clearance. The axial displacement of the rotor and stator are modelled as spring-mass-damper systems. Typically the rotor experiences an external random force due to fluctuations in the bearings surrounding environment. The generality of the proposed random force, which is continuous, stationary, bounded in physical space and has a finite number of frequencies in its spectrum, is potentially transferable to other models of physical phenomena beyond this particular application.

To numerically solve the coupled bearing problem, the modified Reynolds equation and structural equations are simulated simultaneously within a period. Computed results directly give the face clearance and rotor height, whilst post-processing calculations are used to determine the force of the gas on the bearing faces and axial displacement of the stator. Monte Carlo simulations are combined with a derived stroboscopic map solver to evaluate approximations of the minimum face clearance \(g_\mathrm{{min}}\). The probability associated with a specified minimum face clearance \(g_\mathrm{{min}}\) is examined, with face contact corresponding to a zero value of \(g_\mathrm{{min}}\).

Utilising the bearing dynamics allows an investigation into the effect of the external force on the face clearance. Axial displacement of the rotor is due to the imposed external force, however axial displacement of the stator arises from the rotor being forced into close proximity of it. In this case, a peak in the force of the fluid causes the faces to move apart in order to maintain a fluid film. Results are given for an increasing number of realisations in a Monte Carlo simulation, yielding the mean and variance of the minimum face clearance.

The effect of key parameters have been examined, including the pressure gradient across the bearing, value of the bounds of the random variables describing the amplitude of the random force components and the coning angle of the rotor. Outcomes of this type of analysis provide insight to a given bearing geometry to identify safe operating conditions and inform ideal bearing geometries such as in the case of establishing a maximum coning angle for safe operation under given working conditions.