Cartography of the b-plane of a close encounter I: semimajor axes of post-encounter orbits

Abstract

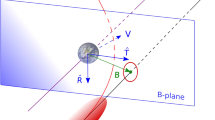
Close planetary encounters play an important role in the evolution of the orbits of small Solar system bodies and are usually studied with the help of numerical integrations. Here we study close encounters in the framework of an analytic theory, focusing on the so-called b-plane, which is the plane centred on the planet and perpendicular to the planetocentric velocity at infinity of the small body. As shown in previous papers, it is possible to identify the initial conditions on the b-plane that lead to post-encounter orbits of given semimajor axis. In this paper we exploit analytical relationships between b-plane coordinates and pre-encounter orbital elements and compute the probability of transition to these post-encounter states, and numerically check the validity of the analytic approach.

Appendix: From coordinates and velocity components at closest approach to b-plane coordinates

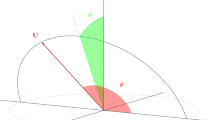
We give here explicit formulae to derive $U, \theta , \phi , \xi , \zeta$ from the planetocentric coordinates and velocity components at closest approach obtained by a numerical integration of the restricted, circular, 3-dimensional 3-body problem.

Let $X_q, Y_q, Z_q, V_x, V_y, V_z$ be the coordinates and velocity components of the small body at the time of closest approach to the planet, in the reference frame of Sect. 2. Then:

$$\begin{aligned} d= & {} \sqrt{X_q^2+Y_q^2+Z_q^2} \\ V= & {} \sqrt{V_X^2+V_Y^2+V_Z^2} \\ c= & {} \frac{md}{V^2d-2m} \\ b= & {} \sqrt{d^2+2cd} \\ U= & {} \frac{Vd}{b} \\ \cos \theta= & {} \frac{VY_qc+V_Ybd}{Vd(c+d)} \\ \sin \theta= & {} \sqrt{1-\cos ^2\theta } \\ \cos \phi= & {} \frac{V_Zbd+VZ_qc}{Vd(c+d)\sin \theta } \\ \sin \phi= & {} \frac{V_Xbd+VX_qc}{Vd(c+d)\sin \theta } \\ \xi= & {} \frac{b(V_ZX_q-V_XZ_q)}{Vd\sin \theta } \\ \zeta= & {} \frac{b(V_Ycd-VY_qb)}{Vd(c+d)\sin \theta }. \end{aligned}$$