Analytical and numerical analysis of tides and salinities in estuaries; part I: tidal wave propagation in convergent estuaries

Abstract

Analytical solutions of the momentum and energy equations for tidal flow are studied. Analytical solutions are well known for prismatic channels but are less well known for converging channels. As most estuaries have a planform with converging channels, the attention in this paper is fully focused on converging tidal channels. It will be shown that the tidal range along converging channels can be described by relatively simple expressions solving the energy and momentum equations (new approaches). The semi-analytical solution of the energy equation includes quadratic (nonlinear) bottom friction. The analytical solution of the continuity and momentum equations is only possible for linearized bottom friction. The linearized analytical solution is presented for sinusoidal tidal waves with and without reflection in strongly convergent (funnel type) channels. Using these approaches, simple and powerful tools (spreadsheet models) for tidal analysis of amplified and damped tidal wave propagation in converging estuaries have been developed. The analytical solutions are compared with the results of numerical solutions and with measured data of the Western Scheldt Estuary in the Netherlands, the Hooghly Estuary in India and the Delaware Estuary in the USA. The analytical solutions show surprisingly good agreement with measured tidal ranges in these large-scale tidal systems. Convergence is found to be dominant in long and deep-converging channels resulting in an amplified tidal range, whereas bottom friction is generally dominant in shallow converging channels resulting in a damped tidal range. Reflection in closed-end channels is important in the most landward 1/3 length of the total channel length. In strongly convergent channels with a single forward propagating tidal wave, there is a phase lead of the horizontal and vertical tide close to 90^o, mimicking a standing wave system (apparent standing wave).

Appendix I

The energy flux balance for depth-integrated tidal flow reads, as:

$$ d\left( {b\overline F } \right)/{\text{dx}} + b\;{D_w} = 0 $$

(1)

$$ b\;{\text{d}}\overline {\text{F}} /{\text{dx}} + \overline {\text{F}} {\text{db}}/{\text{dx}} + b\;{D_w} = 0 $$

(2)

with $\overline F$ = energy flux per unit width per unit time and D _w  = energy dissipation per unit area and time due to bottom friction, b = width of estuary channel, x = horizontal coordinate (positive in landward direction, x = 0 = mouth). The unit of each term is kgm/s³.

Since the work per unit time is defined as the product of force and velocity (=length per unit time), the instantaneous work done by the dynamic pressure force in a vertical section is:

$$ F{ =_o}\int {^h{P_d}\;\overline {\text{u}} \;{\text{dz}}} $$

(3)

The time-averaged (over the wave period) work done by the dynamic pressure force

$$ \overline F = {\left( {1/T} \right)_o}{\int {^T}_o}\int {^h\left( {{P_d}\overline u } \right)dz\;dt} $$

(4)

with, P _d  = ρ g η = instantaneous pressure at height z above bed due to tidal water level variation, η = $\widehat{\eta }$ cos(ωt), $\overline u$ = Q _r /(bh) + $\widehat{{\overline u }}$ cos(ωt + φ) = instantaneous tidal velocity at height z (assumed to be constant over the depth and equal to depth-averaged velocity), h _o = water depth to mean water surface level (h = h _o + η), b = width of estuary, Q _r  = river discharge, φ = phase lead of velocity maximum with respect to water level maximum.

Generally, Q _r  < < Q _tide. Thus:

$$ \begin{array}{*{20}{c}} {\overline F = {{\left( {1/T} \right)}_o}\int {{{^T}_o}\int {^h\left( {\rho \;g\;\eta \;\mu } \right)dz\;dt = \left( {\rho \;g\;{h_o}} \right){{\left( {1/T} \right)}_o}\int {^T\left( {\eta \;\overline u } \right)dt} } } } \hfill \\ {\overline F = \left[ {\rho \;g\;{h_o}\;{Q_r}/\left( {b{h_o}} \right)} \right] + \left[ {\left( {\rho \;g\;{h_o}\;\widehat\eta \;\overline u } \right){{\left( {1/T} \right)}_o}\int {^T} \cos \left( {\omega t} \right)\cos \left( {\omega t + \varphi } \right)dt} \right]} \hfill \\ { \overline F = \left[ {\rho \;g\;{h_o}\;{Q_r}/\left( {b{h_o}} \right)} \right] + \left[ {\left( {0.5\;\rho \;g\;{h_o}\;\overline \eta \;\hat{\bar{u}}} \right)\cos \left( \varphi \right)} \right]} \hfill \\ { \overline F = \left[ {\rho \;g\;{h_o}{Q_r}/\left( {b{h_o}} \right)} \right] + \left[ {\left( {0.25\;g\;{h_o}\;H\;\hat{\bar{u}}} \right)\cos \left( \varphi \right)} \right]} \hfill \\ \end{array} $$

(5)

Using the characteristics of a progressive wave in deep water: $\widehat{{\overline u }}$ = ($\widehat{\eta }$/h _o)c _o = (0.5H/h _o)c _o; φ = 0; $\widehat{\eta }$ = 0.5H; c _o = (gh_o)^0.5 and assuming Q _r = 0, it follows that:

$$ \overline F = 0.125\;\rho \;g\;{H^2}{c_o} = \overline E \;{c_o} $$

(6)

with $\overline E$ = 0.125 ρ g H ² = energy of a wave per unit area, c _o = wave propagation velocity.

Thus, the energy flux per unit width of a progressive wave in deep water is equal to the energy of a wave per unit length of the wave and the wave propagation velocity (similar to the expression used in short wave theory).

The instantaneous energy dissipation per unit area and time due to work done by the bed shear stress is:

$$ {D_w} = {\tau_b}\;\overline u = 0.125\;\rho \;{f^2}\;\overline u = 0.125\;\rho \;f\;{\widehat{{\overline u }}^3}\;{\cos^3}(\omega t) $$

(7)

with τ_b = bed shear stress = 0.125 ρ f $\overline u$ ²_, f = friction coefficient = 8 g/C ², C = Chézy coefficient.

The time-averaged work done by the bed shear stress is:

$$ \begin{array}{*{20}c} {\overline{D} _{w} = 0.125\rho \;f\;\widehat{{\overline{u} }}^{3} {\left( {2/T} \right)}{\int\limits_o^{0.5T} {\cos ^{3} {\left( {\omega t} \right)}dt} }} \\ { = {\left( {1/{\left( {6\pi } \right)}} \right)}\rho \;f\;\widehat{{\overline{u} }}^{3} = {\left( {4/{\left( {3\pi } \right)}} \right)}\rho {\left( {g/C^{2} } \right)}\widehat{{\overline{u} }}^{3} \;} \\ \end{array} $$

(8)

Using linearized friction according to the Lorentz (1922, 1926) method, the same result is obtained.

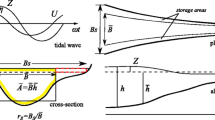
The width and depth of the estuary channel is represented as:

$$ \begin{array}{*{20}{c}} {b{ } = { }{b_o}{ }\exp \left( { - \beta x} \right) = {b_o}\exp \left( { - x/{L_b}} \right)\;{\text{and}}\;{\text{thus}}\;db/dx = - \beta \;{b_o}\exp \left( { - bx} \right) = - \beta \;b} \hfill \\ {h = {h_o}{ }\exp \left( { - gx} \right) = {h_o}{ }\exp \left( { - x/{L_h}} \right)\;{\text{and}}\;{\text{thus}}\;dh/dx = - \gamma \;{h_o}\exp \left( { - \gamma x} \right){ } = - \gamma \;h} \hfill \\ \end{array} $$

(9)

with b _o = width at entrance x = 0, β = 1/L _b  = convergence coefficient, γ = 1/L _h , L _b  = convergence length scale for width, L _h  = convergence length scale for depth. The length scale L _b is of the order of 10–50 km for most estuaries. The length scale L _h is much larger than L _b for most estuaries as the depth generally is fairly constant or very weakly decreasing in landward direction.

Assuming Q _r ≅ 0 (no river discharge), the energy flux balance expression becomes (h _o = water depth to mean sea level at entrance = constant along x; $\widehat{{\overline u }}$ = peak tidal velocity along estuary):

$$ \begin{array}{*{20}l} {{bd\overline{F} /dx + \overline{F} db/dx + b\,D_{w} = 0} \hfill} \\ {{bd{\left[ {\left. {0.25\,\rho \,g\,h\,H\,\widehat{{\overline{u} }}} \right)\cos \varphi } \right]}/dx + {\left[ {0.25\,\rho \,g\,h\,H\,\widehat{{\overline{u} }}\cos \varphi } \right]}[ - \beta \,b] + {\left[ {(1/(6\pi ))\,\rho \,b\,f\,\widehat{{\overline{u} }}^{3} } \right]} = 0} \hfill} \\ {{0.25\,b\,\rho \,g\,\cos \,\varphi \,d{\left[ {h\,H\,\widehat{{\overline{u} }}} \right]}/dx + {\left[ {0.25\,\rho \,g\,h\,H\,\widehat{{\overline{u} }}\cos \varphi } \right]}[ - \beta \,b] + {\left[ {(1/(6\pi ))\,\rho \,b\,f\,\widehat{{\overline{u} }}^{3} } \right]} = 0} \hfill} \\ {{\cos \varphi \,d{\left[ {\left. {h\,H\,\widehat{{\overline{u} }}} \right)} \right]}/dx - \beta \,h\,H\,\widehat{{\overline{u} }}\cos \varphi + {\left[ {(2/(3\pi g))f\,\widehat{{\overline{u} }}^{3} } \right]} = 0} \hfill} \\ {{\cos \,(\varphi ){\left[ {\widehat{{\overline{u} }}H\,dh/dx + \widehat{{\overline{u} }}h\,dH/dx + H\,h\,d\widehat{{\overline{u} }}/dx} \right]} - \beta \,h\,H\,\widehat{{\overline{u} }}\,\cos \varphi + {\left[ {(2/(3\pi g))f\,\widehat{{\overline{u} }}^{3} } \right]} = 0\,} \hfill} \\ \end{array} $$

(10)

Assuming, d $\widehat{{\overline u }}$/dx = ε $\widehat{{\overline u }}$ and dH/dx = ε H (with ε being a small parameter), it follows that: d$\widehat{{\overline u }}$/dx = ($\widehat{{\overline u }}$/H) dH/dx, resulting in:

$$ \begin{array}{*{20}l} {{\cos \varphi {\left[ {\widehat{{\overline{u} }}H{\left( { - \gamma h} \right)} + 2\widehat{{\overline{u} }}\;h\;dH/dx} \right]} - \beta \;h\;H\;\widehat{{\overline{u} }}\cos \varphi + {\left[ {{\left( {2/{\left( {3\pi g} \right)}} \right)}f\widehat{{\overline{u} }}^{3} } \right]} = 0} \hfill} \\ {{dH/dx = 0.5{\left( {\beta + \gamma } \right)}H - \frac{{f\widehat{{\overline{u} }}^{2} }} {{3\pi \;g\;h\;\cos \varphi }}} \hfill} \\ \end{array} $$

(11)

Using $\widehat{{\overline u }} = \left( {0.5H/{h_o}} \right)c\;\cos \varphi$ for a channel of constant depth h _o (see Table 1) and thus γ = 0, it follows that:

$$ dH/dx = 0.5\beta \;H - \frac{{f\;{H^2}{c^2}\;\cos \varphi }}{{12\pi \;g\;{{\left( {{h_o}} \right)}^3}}} $$

(12)

with H = tidal range, β = 1/L _b  = converging length scale (e-folding length scale), h _o = depth (constant), $\widehat{{\overline u }}$ = peak tidal velocity along channel, c = local wave speed, φ = phase difference between horizontal and vertical tide, f = 8 g/C ² = friction coefficient, C = Chézy coefficient, x = horizontal coordinate (positive in landward direction).