1 Introduction

Grouting, which can be defined simply as the injection of suspension or chemical solutions into voids, fissures, and cavities in soil and rock formations to increase strength, to reduce permeability, and to minimize deformations, is a proven ground improvement technique. The selection of the proper grout material must consider project-specific requirements, as well as the geotechnical properties prevailing at the site. In general, chemical grouts are characterized by their superior infiltration capability compared to their cement-based counterparts. On the other hand, permeation grouting through the use of cement-based grouts, which basically consist of grains of various sizes suspended in water, has gained popularity due to its lower cost, more predictable long-term properties, and better environmental compatibility compared to chemical grouting. Consequently, properties and behavior of cement-based grouts have been investigated extensively [1,2,3].

A reliable and accurate evaluation of the groutability (N) of a geomaterial is the principal requirement in any ground improvement project that involves grouting activity. However, the uncertainties due to the rheology and microstructure of the suspension, i.e., colloidal dispersion, electrically charged interfaces, electric double layer, colloid stability, sedimentation, hydration of grout, and pressure filtration make this task a very difficult one [4, 5]. Recent studies indicate that the success of groutability is a complex function of many properties including the grain size distribution of the geomaterial and the grout, the concentration and viscosity of the grout suspension, the pore size and hydraulic conductivity of the soil, and the injection pressure [6, 7]. Thus, earlier prediction studies Burwell [8], De Beer [9], Incecik and Ceren [10], and Mitchell [11] that are based solely on the comparison of grain size or permeability of the base soil with that of the grout resulted in limited success with no universal set of criteria [12].

Due to their heuristic problem-solving capabilities, and the potentially numerous empirical constants as well as the highly complex nature of the problem, artificial intelligence (AI) methods have proved to be viable alternatives for the prediction of groutability [13]. This approach, in general, has the distinct advantage of eliminating the requirement to mathematically describe the problem with an explicit mapping relationship. Liao et al. [6] and Tekin and Akbas [12] have applied artificial neural networks (ANNs) with considerable success for the estimation of the groutability of granular soils with cement grouts. More recently, Cheng and Hoang [13] have proposed another novel AI method, the evolutionary least squares support vector machine inference model, to anticipate the result of grouting process that utilizes microfine cement grout.

The adaptive neuro-fuzzy inference system (ANFIS) [14], which incorporates the modeling capability of fuzzy logic in uncertain scenarios with the adaptive learning strength of ANNs, is also reported to be applicable to simulate complicated problems with indefinite links between the variables [15]. It was employed in various geotechnical engineering applications, such as predicting foundation behavior [16], estimating rock mass modulus [17], modeling the soil effective stress friction angle [18], evaluating stability of tunnels [19], predicting the unconfined compressive strength [20] and swelling potential [21] of compacted soils, determining the permeability of sand [22], developing models for liquefaction triggering, damping ratio, shear modulus, and stress–strain properties of sand–mica mixtures [15], and mapping the spatial variability of rock depth [23]. Although it seems to be a potentially viable solution alternative, ANFIS has not yet been adopted for the prediction of groutability.

This study aims to develop a rule-based simulation for the prediction of groutability through a novel approach, which incorporates the natural language ability of neuro-fuzzy systems and the learning ability of neural networks. Thus, a pioneer work that inquires into the capability of ANFIS for the prediction of groutability is presented. Within this context, employing a database that includes the results of 117 grouting tests, this paper proposes to employ ANFIS to construct an inference model for the prediction of groutability of granular soils with cement grouts. The remaining part of this paper is organized as follows. Existing prediction methods and the ANFIS framework are reviewed followed by a description of the development of the proposed ANFIS model. The results of the application of the ANFIS model with an emphasis on the comparison of the predictive performance of the ANFIS model to the prediction of groutability are then presented and compared against the models that are commonly employed in practice.

2 Existing groutability estimation strategies

Groutability was defined by Burwell [8] and Mitchell [11] as:

$$N = {{\left( {D_{15} } \right)_{\text{base soil}} } \mathord{\left/ {\vphantom {{\left( {D_{15} } \right)_{\text{base soil}} } {\left( {d_{85} } \right)_{\text{cement grout}} }}} \right. \kern-0pt} {\left( {d_{85} } \right)_{\text{cement grout}} }}$$
(1)

in which D15 = particle size of the base soils corresponding to the proportion of grains 15% finer by weight and d85 = particle size of cement grout corresponding to 85% finer. The groutability criterion is satisfied when N is greater than 25. For N smaller than 11, grouting is not possible. For values in between, it was suggested to perform in situ tests to provide data for further evaluation [11].

Burwell [8] suggested another equation for the estimation of grouting potential, even though N is calculated to be greater than 25, using Eq. 1:

$$N = {{\left( {D_{10} } \right)_{\text{base soil}} } \mathord{\left/ {\vphantom {{\left( {D_{10} } \right)_{\text{base soil}} } {\left( {d_{95} } \right)_{\text{cement grout}} }}} \right. \kern-0pt} {\left( {d_{95} } \right)_{\text{cement grout}} }}$$
(2)

in which D10 and d95 are the particle size of the base soils corresponding to the proportion of grains 10% finer by weight and the particle size of cement grout corresponding to 95% finer, respectively. Grouting will be successful when N values exceed 11. If the obtained N values are less than 5, it can be concluded that grouting will not be possible with the selected grout. Similarly, for N values that range between these limits, execution of suitable in situ tests is recommended.

More recently, another similar equation was published by Incecik and Ceren [10] that still considers only the grain size of the cement and that of the soil:

$$N = {{\left( {D_{10} } \right)_{\text{base soil}} } \mathord{\left/ {\vphantom {{\left( {D_{10} } \right)_{\text{base soil}} } {\left( {d_{90} } \right)_{\text{cement grout}} }}} \right. \kern-0pt} {\left( {d_{90} } \right)_{\text{cement grout}} }}$$
(3)

Note that if the N value obtained using Eq. 3 is greater than 10, grouting is possible.

Landry et al. [24] used a slightly different and simpler approach based on the equation developed by De Beer [9], to predict groutability:

$$k = 116\left( {0.7 + 0.034t} \right)\left( {D_{10} } \right)^{2}$$
(4)

where t = temperature (oC) and k = hydraulic conductivity (cm/s). According to Eq. 4, a k value greater than 1 × 10−1 cm/s indicates that the soil is groutable. For 1 × 10−1 cm/s > k > 5 × 10−3 cm/s, a finer cement would be needed. If 5 × 10−3 cm/s > k > 1 x 10−4 cm/s, chemical grouting is warranted to ensure groutability.

Supported by the results of a series of laboratory experiments, the following formula was developed by Akbulut and Saglamer [4], which indicates the requirement for the involvement of supplementary parameters for a robust groutability estimation:

$$N = \frac{{\left( {D_{10} } \right)_{{{\text{base}}\;{\text{soil}}}} }}{{\left( {d_{90} } \right)_{{{\text{cement}}\;{\text{grout}}}} }} + k_{1} \frac{{{w \mathord{\left/ {\vphantom {w c}} \right. \kern-0pt} c}}}{FC} + k_{2} \frac{P}{{D_{r} }}$$
(5)

where w/c = grout’s water–cement ratio, FC = fines content of soil, P = grouting pressure (kPa), and Dr = relative density of the base soil. Based on experimental observations, k1 = 0.5 (dimensionless) and k2 = 0.01 k/Pa are constants to normalize the N values. Based on Eq. 5, if N is greater than 28, cement-based grouting is possible. For N smaller than 28, chemical grouts should be employed.

3 A brief overview of ANFIS

The main objective of the adaptive neuro-fuzzy inference system (ANFIS), which was originally proposed by Jang [14], is to incorporate the most useful properties of neural networks and fuzzy systems. Thus, it incorporates a feed-forward neural network structure within which every layer has a neuro-fuzzy system component [25]. Consequently, ANFIS is suited to generalize and learn from the training data with a particular strength in handling linguistic or fuzzy concepts and finding nonlinear associations between the inputs and outputs [26, 27]. Due to these properties, as indicated in Sect. 1, in recent years, ANFIS has successfully been applied to many geotechnical problems.

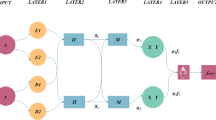
The ANFIS architecture is illustrated in Fig. 1. For the sake of simplicity, a fuzzy inference system with two inputs, x and y, and one output, z, is considered. A typical model incorporating two if–then rules in a first-order Sugeno-type [28] architecture is denoted by:

  1. 1.
    $${\text{If }}x \, = \, A_{1} \;{\text{and}}\;y \, = \, B_{1} ,{\text{ then}}\; \, f_{1} = p_{1} x + q_{1} y + r_{1}$$
    (6)
  2. 2.
    $${\text{If }}x \, = \, A_{2} \;{\text{and }}y \, = \, B_{2} ,{\text{ then}}\; \, f_{2} = p_{2} x + q_{2} y + r_{2}$$
    (7)

in which A1, A2 and B1, B2 are the linguistic labels of membership functions for inputs x and y, respectively; and pi, qi and ri (i = 1 or 2) are linear consequence parameters obtained from the training of the first-order Sugeno fuzzy model. A backpropagation learning algorithm is used to update the membership function. The architecture of ANFIS consists of 5 layers, as summarized below:

Fig. 1
figure 1

Schematic of ANFIS architecture

Full size image

Layer 1 Parameters in this layer are referred to as premise parameters. Each node in this layer creates membership grades for an input variable. The node output OP 1 i is:

$${\text{OP}}_{i}^{1} = \mu_{Ai} \left( x \right){\text{ for }}i \, = \, 1, \, 2{\text{ or}}$$
(8)
$${\text{OP}}_{i}^{1} = \mu_{Bi - 2} \left( y \right){\text{ for }}i \, = \, 3, \, 4$$
(9)

where μ represents the membership function, x (or y) is the input to the node; Ai (or Bi−2) is a fuzzy set related to this node, represented by the shape of the membership functions (MFs) that can be any continuous and piecewise differentiable function such as Gaussian, generalized bell, trapezoidal and triangular. Assuming a triangle-shaped membership function as the MF, the output OP 1 i can be calculated as:

$$\mu_{Ai} (x) = \hbox{max} \left( {\hbox{min} \left( {\frac{{x - a_{i} }}{{b_{i} - a_{i} }},\frac{{c_{i} - x}}{{c_{i} - b_{i} }}} \right),0} \right)$$
(10)

in which the parameter set of membership functions are ai, bi, ci in the premise part of fuzzy if–then rules that changes the shapes of the membership function.

Layer 2 The nodes in this layer, denoted as Π, multiply the incoming signals such that the output \({\text{OP}}_{i}^{2}\) is computed as:

$${\text{OP}}_{i}^{2} = \, w_{i} = \mu_{Ai} \left( x \right)\mu_{Bi} \left( y \right),{\text{ for }}i \, = \, 1, \, 2$$
(11)

Each node output represents the firing strength of a rule.

Layer 3 The ith node of this layer, labeled as N, calculates the normalized firing strengths:

$${\text{OP}}_{i}^{3} = \overline{{w_{i} }} = \frac{{w_{i} }}{{w_{1} + w_{2} }}, \, i \, = \, 1, \, 2$$
(12)

Layer 4 Node i in this layer calculates the contribution of the ith rule toward the model output, using the adaptive node function given as:

$${\text{OP}}_{i}^{4} = \overline{{w_{i} }} f_{i} = \overline{{w_{i} }} \left( {p_{i} x + q_{i} y + r_{i} } \right)$$
(13)

Layer 5 In this layer, the single node calculates the overall output of ANFIS:

$${\text{OP}}_{i}^{5} = \sum\limits_{i} {\overline{{w_{i} }} f_{i} } = \frac{{\sum\nolimits_{i} {w_{i} f_{i} } }}{{\sum\nolimits_{i} {w_{i} } }}$$
(14)

4 Database and ANFIS model development

Based on the complex nature of the groutability problem, a database with case records that have information on w/c, P, Dr, FC, and the grain size distributions of both the grout and the soil is necessary to construct a reliable ANFIS model. For this purpose, the database developed by Tekin and Akbas [12], which includes 117 case records, was employed (Table 1). Thirty-one of the cases presented in Table 1 are from Tekin [29], who examined the penetration capability of the Rheocem 900 cement grout to sand with various grain size distributions and relative densities using the experimental setup shown in Fig. 2. The remaining case records are from Akbulut and Saglamer [4], Zebovitz et al. [30, 31], and Avci [34]. Before ANFIS modeling, the experimental results presented in Table 1 were divided into randomly constructed training, testing and validation subsets within the experimental database with 71% (83 case records), 14.5% (17 case records), and 14.5% (17 case records), respectively, to prevent overfitting, i.e., memorization rather than generalization. These proportions are typical of AI-based modeling studies [13, 15]. As given in Table 2, the training subset is composed of case records that represent the general property range of the whole database. Note that the training subset was repeatedly used to first build and then to fine-tune the connected weights of the networks. Subsequently, the testing data set was employed for the network performance evaluation.

Table 1 Database of groutability tests
Full size table
Fig. 2
figure 2

Test setup

Full size image
Table 2 Some statistical properties of the training and testing subsets of the ANFIS model
Full size table

The neuro-fuzzy modeling was achieved using the fuzzy logic toolbox of MATLAB, version 7.10.0 [31] with the Sugeno-type ANFIS model using a grid partition of the data. Based on the considerations outlined above and considering the available data, the input variables were selected as w/c, Dr, P, FC, and (D15/d85). In order to reach the most effective and robust ANFIS model, a trial and error procedure was employed to estimate the number and types of membership functions (such as triangular, trapezoidal, bell-shaped, Gaussian, sigmoid) for each input variable. The hybrid learning algorithm was selected for tuning the parameters of the Sugeno-type fuzzy inference system.

Model performance as a function of the number and types of membership functions was examined through the root mean square error (RMSE), a statistical parameter defined as:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {f_{i} - y_{i} } \right)^{2} } }$$
(15)

where fi and yi are the experimental and predicted values, respectively, and n is the population size. RMSE measures the degree of accuracy of the model, i.e., the closeness of the observed data points to the model’s predicted values, with lower values indicating a better fit. It also denotes the accuracy of the model in predicting the response [32].

Performance of the ANFIS models with varying number and types of membership functions in terms of RMSE are presented in Table 3. As shown in Table 3, when both the training and the testing subsets are considered, the lowest RMSE was obtained for the ANFIS model with 2, 3, 3, 3, and 3 trapezoid-shaped membership functions (trapmf) for w/c, Dr, P, FC, and (D15/d85) inputs, respectively. The final ANFIS Model has 972 linear parameters, 56 nonlinear parameters, 360 nodes, and 162 fuzzy rules.

Table 3 RMSE of ANFIS models
Full size table

5 Results and discussion

After model development based on the RMSE, the accuracy of the developed ANFIS model has also been examined using the coefficient of correlation (R) as a main criterion. The definition of R is as follows:

$$R = \frac{{n\sum\nolimits_{i = 1}^{n} {\left( {f_{i} y_{i} } \right)} - \sum\nolimits_{i = 1}^{n} {\left( {f_{i} } \right)} \sum\nolimits_{i = 1}^{n} {\left( {y_{i} } \right)} }}{{\sqrt {n\sum\nolimits_{i = 1}^{n} {f_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{n} {f_{i} } } \right)^{2} } \sqrt {n\sum\nolimits_{i = 1}^{n} {y_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{n} {y_{i} } } \right)^{2} } }}$$
(16)

The parameter R basically measures how well the experimental and predicted groutability values are correlated. A correlation coefficient value larger than 0.8 indicates a strong correlation, whereas a value smaller than 0.5 indicates a weak one. Besides its low RMSE value of 0.17 for the testing subset, the accuracy and success of the proposed ANFIS model are also demonstrated by the coefficient of determination (R2) values of 0.90, 0.91, and 0.93 for the training, testing, and validation subsets, respectively.

According to Tekin and Akbas [12], the most important parameters relating to the prediction of groutability in descending order of importance are D15/d85, P, w/c, Dr, and FC, respectively. From a visual perceptive, the influence of input parameters on the output of the ANFIS model is also illustrated in Fig. 3. Here, the variation of model output is plotted against the most influential parameter, D15/d85, and the remaining input parameters. These control action surfaces, which present the relationships between the input parameters and the output, clearly indicate the effective range of the input parameters based on a groutability consideration.

Fig. 3
figure 3

Control action surfaces for ANFIS model

Full size image

The relative merit of the developed ANFIS model with respect to existing groutability estimation procedures is also evaluated. For this purpose, a comparison of the performance of the groutability prediction methods is presented in Table 4. Note that although the number of case histories that are presented in Table 4 is 117, all of the data could not be evaluated by some of the empirical models due to inherent limitations.

Table 4 Comparison of the performance of groutability prediction methods
Full size table

As presented in Table 4, the highest ratio of successful predictions (94.0%) is obtained by the developed ANFIS model. The Burwell [8], Akbulut and Saglamer [4], and ANN [12] methods also have significant success rates. But the Burwell [8] method could only give predictions for 62% of the cases. A closer look at the results presented in Table 4 indicates a very similar success rate for the ANFIS and ANN models. However, it should be mentioned that the proposed ANFIS methodology is clearly defined through membership functions and rules, which are easy to implement as shown in "Appendix", whereas the ANN model has the disadvantage of being a computational tool with relatively difficult access to inherent formulations.

6 Summary and conclusion

In this study, an ANFIS model developed for the prediction of the groutability of granular soils using cement-based grouts. An experimental database consisting of 117 laboratory case records was used to develop the model. The input parameters for the proposed model are, Dr, P, w/c, FC, and (D15)base soil/(d85)cement grout. The proposed ANFIS model demonstrated a high degree of accuracy when estimating groutability, by predicting about 94% of the groutability case records correctly. This success rate could not be achieved by any of the other methods considered except ANN, which uses only 87 of the case records. The results indicate that the ANFIS model is a reliable and accurate tool for predicting groutability.