Abstract
The behaviour of gene regulatory networks (GRNs) is typically analysed using simulation-based statistical testing-like methods. In this paper, we demonstrate that we can replace this approach by a formal verification-like method that gives higher assurance and scalability. We focus on Wagner’s weighted GRN model with varying weights, which is used in evolutionary biology. In the model, weight parameters represent the gene interaction strength that may change due to genetic mutations. For a property of interest, we synthesise the constraints over the parameter space that represent the set of GRNs satisfying the property. We experimentally show that our parameter synthesis procedure computes the mutational robustness of GRNs—an important problem of interest in evolutionary biology—more efficiently than the classical simulation method. We specify the property in linear temporal logic. We employ symbolic bounded model checking and SMT solving to compute the space of GRNs that satisfy the property, which amounts to synthesizing a set of linear constraints on the weights.
Similar content being viewed by others
1 Introduction
Gene regulatory networks (GRNs) are one of the most prevalent and fundamental types of biological networks whose main actors are genes regulating other genes. A topology of a GRN is represented by a graph of interactions among a finite set of genes, where nodes represent genes, and edges denote the type of regulation (activation or repression) between the genes, if any. In [24], Wagner introduced a simple but useful model for GRNs that captures important features of GRNs. In the model, a system state specifies the activity of each gene as a Boolean value. The system is executed in discrete time steps, and all gene values are synchronously and deterministically updated: a gene active at time n affects the value of its neighbouring genes at time \(n+1\). This effect is modelled through two kinds of parameters: threshold parameters assigned to each gene, which specify the strength necessary to sustain the gene’s activity, and weight parameters assigned to pairs of genes, which denote the strength of their directed effect.
Some properties of GRNs can be expressed in linear temporal logic (LTL) (such as reaching a steady-state), where atomic propositions are represented by gene values. A single GRN may or may not satisfy a property of interest. Biologists are often interested in the behavior of populations of GRNs, and in presence of environmental perturbations. For example, the parameters of GRNs from a population may change from one generation to another due to mutations, and the distribution over the different GRNs in a population changes accordingly. We refer to the set of GRNs obtained by varying parameters on a fixed topology as GRN space. For a given population of GRNs instantiated from a GRN space, typical quantities of interest refer to the long-run average behavior. For example, robustness refers to the averaged satisfaction of the property within a population of GRNs, after an extended number of generations. In this context, Wagner’s model of GRN has been used to show that mutational robustness can gradually evolve in GRNs [11], that sexual reproduction can enhance robustness to recombination [1], or to predict the phenotypic effect of mutations. The computational analysis used in these studies relies on explicitly executing GRNs, in the purpose of checking if they satisfy the property. Then, in order to compute the robustness of a population of GRNs, the satisfaction check must be performed repeatedly for many different GRNs. Typically, robustness is estimated by statistically sampling GRNs from the GRN space. In this work, we pursue formal analysis of Wagner’s GRNs which allows to replace this simulation-based statistical testing-type method by a formal verification-type method that gives higher assurance and scalability.
In this paper, we present a novel method for synthesizing the space of parameters which characterize GRNs that satisfy a given property. These constraints eliminate the need for explicitly executing the GRN to check the satisfaction of the property. Importantly, the synthesized parameter constraints allow to efficiently answer questions that are very difficult or impossible to answer by simulation, e.g. emptiness check or parameter sensitivity analysis. In this work, we chose to demonstrate how the synthesized constraints can be used to compute the robustness of a population of GRNs with respect to genetic mutations. Since constraint evaluation is usually faster than executing a GRN, the constraints pre-computation enables faster computation of robustness. To this end, when statistical sampling of the GRNs is employed, higher precision is achieved within the same computational time. Moreover, it sometimes becomes possible to replace the statistical sampling with the exact computation of robustness.
In our method, for a given GRN space and LTL property, we used SMT solving and bounded model checking to generate a set of constraints such that a GRN satisfies the LTL property if and only if its weight parameters satisfy the constraints. The key insight in this method is that the obtained constraints are complex Boolean combinations of linear inequalities. Solving linear constraints has been the focus of both industry and academia for some time. However, the technology for solving linear constraints with Boolean structure, namely SMT solving, has matured only in the last decade [3]. This technology has enabled us to successfully apply an SMT solver to generate the desired constraints.
We have built a tool which computes the constraints for a given GRN space and a property expressed in a fragment of LTL. In order to demonstrate the effectiveness of our method, we computed the robustness of five GRNs listed in [8], and for three GRNs known to exhibit oscillatory behavior. We first synthesised the constraints and then we used them to estimate robustness based on statistical sampling of GRNs from the GRN space. Then, in order to compare the performance with the simulation-based methods, we implemented the approximate computation of robustness, where the satisfiability of the property is verified by executing the GRNs explicitly. The results show that in six out of eight tested networks, the pre-computation of constraints provides greater efficiency, performing up to three times faster than the simulation method.
In the benchmarks, we compute mutational robustness with respect to mutation model without selection, described in Sect. 7.2. In this model, the GRNs in a GRN-population are assumed to be distributed so that the mutation process from one generation to another is not influenced by evolutionary pressure (there is no priority given to cells which exhibit some selection property). Mathematically, the limiting distribution of such evolutionary process over many generations amounts to the stationary distribution of a discrete-time, finite Markov chain, where the state space captures all possible GRN configurations in a GRN-space, and transition probabilities describe the probability that one GRN configuration changes to another one in the next generation; Such stationary distribution can be approximated with complexity polynomial in the size of GRN-space. This model was also used in our related work in [17]. We here extend the approach by introducing a more realistic, but also technically more demanding, model with selection. In this model, a number of individuals not satisfying the selection property dies, while those individuals who meet the property reproduce more, that is, the nature selects for the individuals satisfying the property. We take the selection property to be equal to the property we check robustness for. To this end, the process describing the GRN space over generations is not Markovian. In Sect. 7.3, the principal result is Theorem 2, which shows that robustness for the model with selection equals the second largest eigenvalue of the matrix capturing the transition probabilities of mutations among the GRNs in the GRN space. Moreover, in Theorem 3, we show that, confirming the intuition, in both model with and without selection, robustness measure preserves monotonicity in the sense that larger properties imply larger robustness.
Related Work Formal verification techniques are already used for aiding various aspects of biological research [12, 15, 19, 20, 25]. The robustness of models of biochemical systems with respect to temporal properties has been studied [6, 18, 22]. These approaches differ from ours in that in our work we focus on quantifying robustness with respect to a concrete source of perturbation of the parameters (such as point mutations). In [18] and [22], the authors present methods to evaluate the satisfaction degree of a trace with respect to a temporal formula, but no assumption is made on the distribution of parameters, while in [6], the authors use a symbolic technique to synthesise the parameter space for which the property is satisfied, but robustness is defined in terms of the relative size of the error intervals around some reference parameter values.
This work extends [17] which, to the best of our knowledge, is the first application of formal verification to studying the robustness against evolution of gene regulatory networks. As such, this work opens up a novel application area for the formal verification community. As previously discussed, with respect to related studies in evolutionary biology, our method can offer a higher degree of assurance, more accuracy, and better scalability than the traditional, simulation-based approaches. In addition, while previous works focus on invariant properties, our method allows the study of non-trivial temporal properties that are expressible in LTL, such as bistability or oscillations between gene states.
1.1 Motivating example
In the following, we will illustrate the main idea of the paper on an example of a GRN space \(T\) generated from the GRN network shown in Fig. 1a. Two genes A and B inhibit each other, and both genes have a self-activating loop. The parameters \((i_A,i_B)\) represent constant inputs, which we assume to be regulated by some other genes that are not presented in the figure. Each of the genes is assigned a threshold value (\(t_A\), \(t_B\)), and each edge is assigned a weight (\(w_{AA}\), \(w_{AB}\), \(w_{BA}\), \(w_{BB}\)). The dynamics of a GRN-individual chosen from \(T\) depends on these parameters. Genes are in either active or inactive state, which we represent with Boolean variables. For a given initial state of all genes, and for fixed values of weights and thresholds, the values of all genes evolve deterministically in discrete time-steps that are synchronized over all genes. Let \(a\) (resp. \(b\)) be the Boolean variable representing the activity of gene A (resp. B). We denote a GRN state by a pair \((a,b)\). Let \(\tau \) be the function that governs the dynamics of \(\mathcal {G}\) (see Def. 3):
The next state of a gene is the result of arithmetically adding the influence from other active genes.
Motivating example. a The topology of a GRN with mutual inhibition of genes A and B. b The labelled transition system where labels denote the linear constraints which enable the transition. \(\alpha _0\), \(\alpha _1\), \(\beta _0\), and \(\beta _1\) denote linear atomic formulas \(i_A - w_{BA} \le t_A\), \(i_B+w_{BB} > t_B\), \(i_B - w_{AB} \le t_B\), and \(i_A+w_{AA} > t_A\) respectively. c Run-times comparison between execution method (dashed lines) and our evaluation method (solid lines)
The topology of mutually inhibiting pair of genes is known to be bistable: whenever one gene is highly expressed and the other is barely expressed, the system remains stable [16, 22]. The bistability property can be written as the following LTL formula (see Def. 4):
Let us fix values for parameters \(t_A=t_B=0.6\), \(w_{AB}=w_{BA}=w_{BB}=0.3\), and \(i_A=i_B= \frac{2}{3}\). Then, we can check that a GRN is bistable by executing the GRN. Indeed, for the given parameter values, the states (0, 1) and (1, 0) are fixed points of \(\tau \). In other words, the GRN with those parameter values have two stable states: if they start in state (0, 1) (resp. (1, 0)), they remain there. Now let us choose \(i_A=\frac{2}{3}\), \(i_B=\frac{1}{3}\). By executing the GRN, we can conclude that it does not satisfy the property: at state (0, 1), B does not have sufficiently strong activation to surpass its threshold and the system jumps to (0, 0). Intuitively, since the external activation of B is too small, the phenotype has changed to a single stable state. In general, it is not hard to check by inspection that the bistability property will be met by any choice of parameters satisfying the following constraints:
Let’s now suppose that we want to compute the robustness of \(T\) in presence of variations on edges due to mutations. Then, for each possible value of parameters, one needs to verify if the respective GRN satisfies the property. Using the constraints (1), one may verify GRNs without executing them.
Our method automatizes this idea to any given GRN topology and any property specified in LTL. We first translate \(T\) to a labelled transition system, partly shown in Fig. 1b. Then, we apply symbolic model checking to compute the constraints which represent the space of GRNs from \(T\) that satisfy the bi-stability property.
To illustrate the scalability of our method in comparison with the standard methods, in Fig. 1c, we compare the performance of computing the mutational robustness with and without precomputing the constraints (referred to as evaluation and execution method respectively). We choose a mutation model such that each parameter takes 13 possible values distributed according to the binomial distribution (see Sect. 7 for more details on the mutation model). We estimate the robustness value by statistical sampling of the possible parameter values. For a small number of samples, our method is slower because we spend extra time in computing the constraints. However, more samples may be necessary for achieving the desired precision. As the number of samples increases, our method becomes faster, because each evaluation of the constraints is two times faster than checking bistability by executing GRN-individuals. For \(1.2\times 10^5\) simulations, execution and evaluation methods take same total time, and the robustness value estimated from these many samples lies in the interval (0.8871, 0.8907) with 95 % confidence. Hence, for this GRN, if one needs better precision for the robustness value, our method is preferred.
One may think that for this example, we may compute exact robustness because the number of parameter values is only \(13^6\) (four weights and two inputs). For simplicity of illustration, we chose this example, and we later present examples with a much larger space of parameters, for which exact computation of robustness is infeasible.
2 Preliminaries
In this section, we start by defining a GRN space, which will serve to specify common features for GRNs from the same population. These common features are types of gene interactions (topology), constant parameters (thresholds), and ranges of parameter values that are subject to some environmental perturbation (weights). Then, we formally introduce a model of an individual GRN from the GRN space and temporal logic to express its properties.
2.1 Basic notation
\(\mathbb {R}_{\ge 0}\) (resp. \(\mathbb {Q}_{\ge 0}\)) is the set of non-negative real (resp. rational) numbers. For \(m < n\), let m..n denote the set of integers from m to n. We denote real vectors by bold face letters. Let \(\mathbf {k}\) be a real vector then let \(k_i\) denote the ith element of \(\mathbf {k}\). With abuse of notation, we treat finite maps with ordered domain as vectors with size of the map. Let S be a set, we denote as \(\mathcal {P}_k(S)\) the set of all subsets of S with cardinality k.
For rationals constants \(k_1,\ldots ,k_n\), a vector of rational variables \(v= (v_1,\ldots ,v_n)\), and a rational constant t, let \( k_1v_1 + \cdots + k_nv_n + t\) denote a linear term. Let \(k_1v_1 + \cdots + k_nv_n + t > 0 \) and \(k_1v_1 + \cdots + k_nv_n + t \ge 0\) be a strict and non-strict inequality over \(v\) respectively. Let \(\textit{linear}(v)\) be the set of all the (non-)strict inequalities over \(v\). Let \(\textit{polyhedra}(v)\) be the set of all the finite conjunctions of the elements of \(\textit{linear}(v)\).
2.2 GRN space
The key characteristics of the behaviour of a GRN are typically summarised by a directed graph where nodes represent genes and edges denote the type of regulation between the genes. A regulation edge is either activation (one gene’s activity increases the activity of the other gene) or repression (one gene’s activity decreases the activity of the other gene) [23]. In Wagner’s model of a GRN, in addition to the activation types between genes, each gene is assigned a threshold and each edge (pair of genes) is assigned a weight. The threshold of a gene models the amount of activation level necessary to sustain activity of the gene. The weight on an edge quantifies the influence of the source gene on destination gene of the edge.
We extend the Wagner’s model by allowing a range of values for weight parameters. We call our model GRN space, denoting that all GRNs instantiated from that space share the same topology, and their parameters fall into given ranges. We assume that each gene always has some minimum level of expression without any external influence. In the model, this constant input is incorporated by a special gene which is always active, and activates all other genes from the network. The weight on the edge between the special gene and some other gene represents the minimum level of activation. The minimal activation is also subject to perturbation.
Definition 1
(GRN space) A GRN space is a tuple

where
-
\(G=\{g_1,\ldots ,g_{d}\}\) is a finite ordered set of genes,
-
\(g_{in} \in G\) is the special gene used to model the constant input for all genes,
-
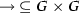 is the activation relation such that
is the activation relation such that 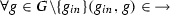 and
and 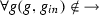 ,
, -
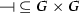 is the repression relation such that
is the repression relation such that 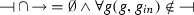 ,
, -
\(t:G\rightarrow \mathbb {Q}\) is the threshold function such that \(\forall g\in G{\setminus }\{g_{in}\} t(g) \ge 0\) and \(t(g_{in}) < 0 \),
-
 is the maximum value of an activation/repression,
is the maximum value of an activation/repression, -
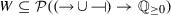 assigns a set of possible weight functions to each activation/inhibition relation, so that
assigns a set of possible weight functions to each activation/inhibition relation, so that 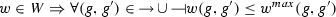 .
.
In the following text, if not explicitly specified otherwise, we will be referring to the GRN space .
.
2.3 GRN-individual
Definition 2
(GRN-individual) A GRN-individual \(\mathcal {G}\) is a pair \((T,w)\), where \(w\in {W}\) is a weight function from the GRN space.
A state \(\mathbf {\sigma }:G\rightarrow \mathbb {B}\) of a GRN-individual \(\mathcal {G}= (T,w)\) denotes the activation state of each gene in terms of a Boolean value. Let \(\varSigma (\mathcal {G})\) denote the set of all states of \(\mathcal {G}\), such that \(\mathbf {\sigma }(g_{in})=true\). In the context where we do not refer to a set of states of a concrete GRN-individual, we denote by \(\varSigma (T)\) the set of all states of any GRN from GRN space \(T\). The GRN model executes in discrete time steps by updating all the activation states synchronously and deterministically according to the following rule: a gene is active at next time if and only if the total influence on that gene, from genes active at current time, surpasses its threshold.
Definition 3
(Semantics of a GRN-individual) A run of a GRN-individual\(\mathcal {G}= (T,w)\) is an infinite sequence of states \(\mathbf {\sigma }_0, \mathbf {\sigma }_1, \ldots \) such that \(\mathbf {\sigma }_n \in \varSigma (\mathcal {G})\) and \(\tau (\mathbf {\sigma }_n) = \mathbf {\sigma }_{n+1}\) for all \(n \ge 0\), where \(\tau :\varSigma (\mathcal {G}) \rightarrow \varSigma (\mathcal {G})\) is a deterministic transition function defined by

The language of \(\mathcal {G}\), denoted by \(\llbracket \mathcal {G}\rrbracket \), is a set of all possible runs of \(\mathcal {G}\). Note that a GRN-individualdoes not specify the initial state. Therefore, \(\llbracket \mathcal {G}\rrbracket \) may contain more than one run.
2.4 Temporal properties
A GRN exists in a living organism to exhibit certain behaviors. Here we present a linear temporal logic (LTL) to express the expected behaviors of GRNs.
Definition 4
(Syntax of Linear Temporal properties) The grammar of the language of linear temporal logic formulae is given by the following rules
where \(g\in G\) is a gene.
Linear temporal properties are evaluated over all (in)finite runs of states from \(\varSigma (G)\). Let us consider a run \(r = \mathbf {\sigma }_1,\mathbf {\sigma }_2,\mathbf {\sigma }_3,\ldots \in \varSigma (G)^{*} \cup \varSigma (G)^{\infty }\). Let \(r^i\) be the suffix of r after i states and \(r_i\) is the ith state of r. The satisfaction relation \(\models \) between a run and an LTL formula is defined as follows:
Note that if \(|r| < i\) then \(r^i\) has no meaning. In such a situation, the above semantics returns undefined, i.e., r is too short to decide the LTL formula. We say a language \(\mathcal{L}\models \varphi \) if for each run \(r \in \mathcal{L}\), \(r \models \varphi \), and a GRN \(\mathcal {G}\models \varphi \) if \(\llbracket \mathcal {G}\rrbracket \models \varphi \). Let \(\Diamond \varphi \) be shorthand for \(true \mathcal {U}\varphi \) and \(\Box \varphi \) be shorthand for \(\lnot \Diamond \lnot \varphi \).
Note that we did not include next operator in the definition of LTL. This is because a typical GRN does not expect something is to be done in the strictly next cycle.
The algorithm for model checking LTL properties on a GRN-individualalways halts on runs shorter or equal to the number of states \(\varSigma (G)\), because the GRN-individualis deterministic (every infinite path is fully described by its prefix of length \(|\varSigma (G)|\)). Hence it will suffice to perform bounded model checking for paths of length up to \(|\varSigma (G)|\).
3 Algorithm for parameter synthesis
In this section we present an algorithm for synthesising the weights’ space corresponding to a given property in linear temporal logic. The method combines LTL model checking [2] and satisfiability modulo theory (SMT) solving [4].
The method operates in two steps. First, we represent any GRN-individualfrom the GRN space with a parametrized transition system. In this system, a transition exists between every two states, and it is labelled by linear constraints, that are necessary and sufficient constraints to enable that transition in a concrete GRN-individual (for example, see Fig. 1b). We say that a run of the parametrized transition system is feasible if the conjunction of all the constraints labelled along the run is satisfiable. Second, we search for all the feasible runs that satisfy the desired LTL property and we record the constraints collected along them. The disjunction of such run constraints fully characterizes the regions of weights which ensure that LTL property holds in the respective GRN-individual.
Definition 5
(Parametrized transition system) For a given GRN space \(T\) and rational parameters map \(v: G\rightarrow V\), the parametrized transition system \((T, v)\) is a labelled transition system \((\varSigma (T), \varPhi )\), where the labeling of edges \(\varPhi : \varSigma (T) \times \varSigma (T) \rightarrow polyhedra(v)\) is defined as follows:

\(\varPhi (\mathbf {\sigma },\mathbf {\sigma }')\) says that a gene \(g'\) is active in \(\mathbf {\sigma }'\) iff the weighted sum of activation and suppression activity of the regulators of \(g'\) is above its threshold.
A run of \((T, v)\) is a sequence of states \(\mathbf {\sigma }_0, \mathbf {\sigma }_1, \ldots \) such that \(\mathbf {\sigma }_n \in \varSigma (T)\) for all \(n \ge 0\), and \(\varPhi (\mathbf {\sigma }_0,\mathbf {\sigma }_{1}) \wedge \varPhi (\mathbf {\sigma }_1,\mathbf {\sigma }_{2}) \wedge \ldots \) is said to be the run constraint of the run. A run is feasible if its run constraint is satisfiable. We denote by \(\llbracket (T,v)\rrbracket \) the set of feasible traces for \((T,v)\). For a weight function \({w}\), let \(\varPhi (\mathbf {\sigma }, \mathbf {\sigma }')[{w}/v]\) denote the formula obtained by substituting \(v\) by \({w}\) and let \((T, v)[{w}/v] = (\varSigma (T), \varPhi ')\), where \(\varPhi '(\mathbf {\sigma },\mathbf {\sigma }') = \varPhi (\mathbf {\sigma },\mathbf {\sigma }')[{w}/v]\) for each \(\mathbf {\sigma },\mathbf {\sigma }' \in \varSigma (T)\).
In the following text, we refer to the parametrized transition system \((T, v)\) and an LTL property \(\varphi \). Moreover, we denote the run constraint of run \(r=\mathbf {\sigma }_0,\mathbf {\sigma }_1,\ldots \in \llbracket (T,v)\rrbracket \) by \({cons}(r)\).
Lemma 1
For a weight function \({w}\), the set of feasible runs of \((T, v)[{w}/v]\) is equal to the language of \((T,w)\), that is \(\llbracket (T,{w})\rrbracket \).
The proof of the above lemma follows from the definition of the semantics for GRN-individual. Note that the run constraints are conjunctions of linear (non)-strict inequalities. Therefore, we may apply efficient SMT solvers to analyze \((T, v)\).
3.1 Constraint generation via model checking
Now our goal is to synthesize the constraints over \(v\) which characterise exactly the set of weight functions \(w\), for which \((T,{w})\) satisfies \(\varphi \). Each feasible run violating \(\varphi \) reports a set of constraints which weight parameters should avoid. Once all runs violating \(\varphi \) are accounted for, the desired region of weights is completely characterized. More explicitly, the desired space of weights is obtained by conjuncting negations of run constraints of all feasible runs that satisfy \(\lnot \varphi \).
In Fig. 2, we present our algorithm GenCons for the constraint generation. GenCons unfolds \((T, v)\) in depth-first-order manner to search for runs which satisfy \(\lnot \varphi \). At line 3, GenCons calls recursive function GenConsRec to do the unfolding for each state in \(\varSigma (T)\). GenConsRec takes six input parameters. The parameter \(run.\mathbf {\sigma }\) and runCons are the states of the currently traced run and its respective run constraint. The third parameter are the constraints, collected due to the discovery of counterexamples, i.e., runs which violate \(\varphi \). The fourth, fifth and sixth parameter are the description of the input transition system and the LTL property \(\varphi \). Since GRN-individuals have deterministic transitions, we only need to look for the lassos up to length \(|\varSigma (T)|\) for LTL model checking. To see this, notice that, even though the parametrised transition system is non-deterministic, every feasible run is a run of a GRN-individual, and its behaviour (and hence evaluation of an LTL formula) is fully determined by prefixes of length \(|\varSigma (T)|\). Therefore, we execute the loop at line 6 only if the \(run.\mathbf {\sigma }\) has length smaller than \(|\varSigma (T)|\). The loop iterates over each state in \(\varSigma (T)\). The condition at line 8 checks if \(run.\mathbf {\sigma }\mathbf {\sigma }'\) is feasible and, if it is not, the loop goes to another iteration. Otherwise, the condition at line 9 checks if \(run.\mathbf {\sigma }\mathbf {\sigma }' \models \lnot \varphi \). Note that \(run.\mathbf {\sigma }\mathbf {\sigma }' \models \lnot \varphi \) may also return undefined because the run may be too short to decide the LTL property. If the condition returns true, we add negation of the run constraint in goodCons. Otherwise, we make a recursive call to extend the run at line 12. goodCons tells us the set of values of \(v\) for which we have discovered no counterexample. GenCons returns goodCons at the end.
Counterexample guided computation of the mutation space feasible wrt. \(\varphi \). Let “.” be an operator that appends two sequences. \(run.\mathbf {\sigma }\mathbf {\sigma }' \models \lnot \varphi \) can be implemented by converting \(\lnot \varphi \) into a Büchi automaton and searching for an accepting run over \(run.\mathbf {\sigma }\mathbf {\sigma }'\). However, a finite path may be too short to decide whether \(\varphi \) holds or not. In that case, the condition at line 9 fails. Since \(( T, v)\) is finite, the finite runs are bound to form lassos within \(|\varSigma (T)|\) steps. If a finite run forms a lasso, then the truth value of \(run.\mathbf {\sigma }\mathbf {\sigma }' \models \lnot \varphi \) will be determined
Since run constraints are always a conjunction of linear inequalities, goodCons is a conjunction of clauses over linear inequalities. Therefore, we can apply efficient SMT technology to evaluate the condition at line 8. The following theorem states that the algorithm GenCons computes the parameter region which satisfies property \(\varphi \).
Theorem 1
The desired set of weight functions for which a GRN-individual satisfies \(\varphi \) equals the weight functions which satisfy the constraints returned by \(\textsc {GenCons} \):
Proof
The statement amounts to showing that the sets \(A = \{w\mid (T,w)\models \varphi \}\) and \(B = \bigcap _{r\in \llbracket (T,v)\rrbracket \wedge r\models \lnot \varphi }\{w\mid w\models \lnot {cons}(r)\}\) are equivalent. Notice that
\(\square \)
We use the above presentation of the algorithm for easy readability. However, our implementation of the above algorithm differs significantly from the presentation. We follow the encoding of [7] to encode the path exploration as a bounded-model checking problem. Further details about implementation are available in Sect. 5. The algorithm has exponential complexity in the size of \(T\). However, one may view the above procedure as the clause learning in SMT solvers, where clauses are learnt when the LTL formula is violated [26]. Similar to SMT solvers, in practice, this algorithm may not suffer from the worst-case complexity.
Example 1
The GRN osc3 (shown in Fig. 3) was the model of a pioneering work in synthetic biology [14], and it is known to provide oscillatory behaviour: each gene should alternate its expression between ‘on’ and ‘off’ state:
Intuitively, since each gene is only down-regulated by other genes, in order to switch on any of the genes, the constitutive input alone must be bigger than threshold. Moreover, in order to switch off a gene whenever its repressor is on, its constitutive input minus the repression weight should be lower than the threshold. It is then easy to inspect that these conditions are also sufficient for oscillatory behaviour, and hence the solutions are the constraints:
GRN benchmarks. mi, misa (mutual inhibition), qi (quad inhibition), and ncc (cell cycle switch) satisfy different forms of bistability. For the networks ci (cell cycle switch), the value of gene eventually stabilizes [9]. In osc3, also known as the repressilator [14], the gene values alternate. osc5 and osc7 (not shown) are generalizations of osc3, and also exhibit oscilating behavior
4 Computing robustness
In this section, we present an application of our parameter synthesis algorithm, namely computing robustness of GRNs in presence of mutations. To this end, we formalize GRN-populationand its robustness. Then, we present a method to compute the robustness using our synthesized parameters.
A GRN-populationmodels a large number of GRN-individuals with varying weights. All the GRN-individuals are defined over the same GRN space, hence they differ only in their weight functions. The GRN-populationis characterised by the GRN space \(T\) and a probability distribution over the weight functions. In the experimental section, we will use the range of weights \({W}\) and the distribution \(\pi \) based on the mutation model outlined in Sect. 7.
Definition 6
(GRN-population) A GRN-population \(\mathcal {Z}\) is a pair \((T,\pi )\), where \(\pi :{W}\rightarrow [0,1]\) is a probability distribution over all weight functions from GRN space \(T\).
We write \(\varphi ({\mathcal {Z}})\in [0,1]\) to denote the expectation that a GRN instantiated from a GRN-population \(\mathcal {Z}=(T,\pi )\) satisfies \(\varphi \). The value \(\varphi ({\mathcal {Z}})\) is in the interval [0, 1] and we call it robustness.
Definition 7
(Robustness) Let \(\mathcal {Z}=(T,\pi )\) be a GRN-population, and \(\varphi \) be an LTL formula which expresses the desired LTL property. Then, robustness of \(\mathcal {Z}\) with respect to property \(\varphi \) is given by
The above definition extends that of [11], because it allows for expressing any LTL property as a phenotype, and hence it can capture more complex properties such as oscillatory behaviour.
The mutation model that induces the GRN-population we use in our experimental evaluation is shown in Sect. 7.
4.1 Evaluating robustness
Let us suppose we get a GRN-population \(\mathcal {Z}= ( T, \pi )\) and LTL property \(\varphi \) as input to compute robustness.
For small size of GRN space \(T\), robustness can be computed by explicitly enumerating all the GRN-individuals from \(T\), and verifying each GRN-individual against \(\varphi \). The probabilities of all satisfying GRN-individuals are added up. However, the exhaustive enumeration of the GRN space is often intractable due to a large range of weight functions \({W}\) in \(T\). In those cases, the robustness is estimated statistically: a number of GRN-individuals are sampled from \(T\) according to the distribution \(\pi \), and the fraction of satisfying GRN-individuals is stored. The sampling experiment is repeated a number of times, and the mean (respectively variance) of the stored values are reported as robustness (respectively precision).
5 Implementation
In this section, we show the details of the implementation of the algorithms for parameter synthesis and for evaluating robustness.Footnote 1 The implementation includes heuristics and data structures which improved efficiency. The workflow consists of the following steps: given a GRN-space and an LTL property we perform
-
encoding the bounded model checking (BMC) of the parametrised transition system as a satisfiability problem,
-
computation of goodCons by quantifier elimination,
-
minimization of goodCons using linear decision diagrams (LDDs),
-
sampling of mutants with efficient property checking,
where the last step returns an estimate of the robustness value.
5.1 Encoding the bounded model-checking problem
We encode the model checking of a parameterized transition system against the LTL property into a first-order logic formula over linear real arithmetic. The result is a formula over the real variables \(w_{g, g'}\), where \(g, g' \in G\) are such that either  or
or  , representing all weight function of a GRN-space \(T\) for which the LTL property \(\phi \) is satisfied. Let \(k \in \mathbb {N}_{>0}\) be a bound, we define the encoding of the bounded model-checking problem as \(\llbracket T, \lnot \varphi \rrbracket _k\) such that the formula \(\llbracket T, \lnot \varphi \rrbracket _k\) is satisfiable iff there exists a run \(r\in \llbracket (T,{w})\rrbracket \) of length k that does not satisfy \(\varphi \). The encoding consists of the conjunction of two main subformulae, i.e. \(\llbracket T, \lnot \varphi \rrbracket _k := \llbracket T\rrbracket _k \wedge \llbracket \lnot \varphi \rrbracket _k\), where
, representing all weight function of a GRN-space \(T\) for which the LTL property \(\phi \) is satisfied. Let \(k \in \mathbb {N}_{>0}\) be a bound, we define the encoding of the bounded model-checking problem as \(\llbracket T, \lnot \varphi \rrbracket _k\) such that the formula \(\llbracket T, \lnot \varphi \rrbracket _k\) is satisfiable iff there exists a run \(r\in \llbracket (T,{w})\rrbracket \) of length k that does not satisfy \(\varphi \). The encoding consists of the conjunction of two main subformulae, i.e. \(\llbracket T, \lnot \varphi \rrbracket _k := \llbracket T\rrbracket _k \wedge \llbracket \lnot \varphi \rrbracket _k\), where
-
\(\llbracket T\rrbracket _k\) is the unrolling of the transition relation induced by \(T\), and
-
\(\llbracket \lnot \varphi \rrbracket _k\) is the propositional encoding of the bounded semantics of \(\lnot \varphi \).
For each gene \(g\in G\), we introduce \(k+1\) propositional symbols \(g^i\), with \(0 \le i \le k\), encoding the expression of gene \(g\) at step i. Let  be the set of regulators of \(g' \in G\). We define the formulae \(\textit{States}(T, i, G_1, g')\) and \(Weights(T, G_1, g')\), with \(0 \le i \le k\), \(G_1\subseteq G\) and \(g' \in G\). The first encodes all states at step i where only the regulators of \(g'\) that are in \(G_1\) are on, and the second encodes the weight functions for which \(g'\) gets activated where only the regulators of \(g'\) that are in \(G_1\) are on, i.e.,
be the set of regulators of \(g' \in G\). We define the formulae \(\textit{States}(T, i, G_1, g')\) and \(Weights(T, G_1, g')\), with \(0 \le i \le k\), \(G_1\subseteq G\) and \(g' \in G\). The first encodes all states at step i where only the regulators of \(g'\) that are in \(G_1\) are on, and the second encodes the weight functions for which \(g'\) gets activated where only the regulators of \(g'\) that are in \(G_1\) are on, i.e.,


The formula \(\textit{Step}(T, i, j)\), with \(0 \le i,j \le k\), encodes a transition between step i and step j, i.e.,
The unrolling of the transition relation is defined as the conjuction of k consecutive steps, i.e., \(\llbracket T\rrbracket _k := \bigwedge _{1 \le i \le k} Step(T, i-1, i)\). The bounded semantics of \(\lnot \varphi \) (Definition 4) is encoded as in [7]. Hence, the formula \(\llbracket T, \lnot \varphi \rrbracket _k\) denotes all feasible runs of length k that violate the property \(\varphi \). Finally, the encoder produces the quantified formula \(\lnot \exists g_1^0, \ldots ,g_d^k :\llbracket T, \lnot \varphi \rrbracket _k\), where \(g_1^0, \ldots ,g_d^k\) are the \((k+1) \cdot d\) propositional variables encoding gene expression. Intuitively, the formula \(g_1^0, \ldots ,g_d^k :\llbracket T, \lnot \varphi \rrbracket _k\) encodes all weight functions such that there exists a run of length k that violates \(\varphi \), hence its negation encodes all weight functions for which all runs of length k satisfy \(\varphi \).
5.2 Symbolic computation of goodCons
The symbolic computation procedure consists of eliminating all quantified symbols \(g_1^0, \ldots ,g_d^k\) producing a quantifier-free formula equivalent to \(\lnot \exists g_1^0, \ldots ,g_d^k :\llbracket T, \lnot \varphi \rrbracket _k\), and hence equivalent to goodCons. We implement the quantifier elimination procedure as shown in the following algorithm:

The quantifier elimination is solved for incremental bounds: we use the formula \(\psi \) to store the unrolling up to k and

to accumulate the result. At every iteration, line 5 encodes the BMC problem of length k, additionally excluding all weight functions that have been previously ruled out by the BMC problems of shorter lengths. The actual quantifier-elimination is performed by the loop at line 6. The condition of the loop queries the SMT-solver for an assignment \(\mu \) to the free atomic propositions of the formula \(\phi '\). As all propositional variables have been quantified, the free atomic proposition are all linear constraints for the weight function (Eq. ), hence \(\mu \) is in the form of a conjuction of linear constraints. The assignment is blocked in formula \(\phi '\) and accumulated in

. We implemented the symbolic computation of goodCons using the Z3 SMT-solver [13], specifically tailored to enumerate partial assignments on the boolean structure of the formula, similarly to [21]. The reduction in the size of the assignment yields a reduction in the number of iterations of inner loop (line 6), as more future assignments are possibly blocked.
5.3 Minimization of goodCons by efficient representation
We use linear decision diagrams (LDD) [10] for representing formula goodCons. A linear decision diagram is a binary decision diagram where non-terminal nodes are labelled by linear constraints and terminal nodes are labelled by either 0 or 1. A function \(w\) satisfies a non-terminal node if \(w\) satisfies the label and satisfies the left child or if \(w\) does not satisfy the label and satisfies the right child, while it satisfies a terminal node if the label is 1. The LDD produced by the parameter synthesis procedure is an LDD over the variables \(w_{g,g'}\) such that, for all weight functions \(w\in {W}\) of \(T\), \(w\) satisfies the LDD iff \(\llbracket (T,{w})\rrbracket \models \varphi \). The representation of the formula goodCons by means of LDD enjoys the property of being minimal, provided an ordering for the linear constraints over \(w_{g, g'}\). Moreover, LDDs inherit optimizations and variable reordering algorithms from BDDs. We implement LDDs by using the CUDD BDD package, where propositional variables are mapped to linear constraints of the original goodCons formula. In general, the BDD package does not contain information about the theory of linear real arithmetics used by the constraints, hence a satisfying assignment for a BDD, might be unsatisfiable when considering the semantics of the constraints. Our implementation ensures consistency against the theory because of the fact that we represent goodCons using LDD, after checking the models \(\mu \) with the SMT solver. The LDD accumulates models \(\mu \) at line 8 that are ensured to be consistent with the theory, as they are models for \(\psi '\), extracted at line 6.
5.4 Sampling with efficient property checking
The robustness evaluation procedure takes a probability distribution \(\pi :{W}\rightarrow [0,1]\) over the weight functions of \(T\) and computes the expected probability of satisfying property \(\varphi \), as in Def. . The procedure samples a number of weight functions from \(\pi \) and computes the ratio between functions that induce GRN-individuals that satisfy the property and the number of samples.
Depending on how a GRN-individualinduced by a sample function is verified against the LTL property, we have two methods:
-
In the first method, which we will call execution method, each sampled GRN-individualis verified by explicitly executing each run of the GRN-individualfrom each initial state and checking if each run satisfies \(\varphi \);
-
In the second method, which we will call evaluation method, the constraints are first precomputed, and each sampled function is verified by evaluating it in the produced LDD.
Clearly, the time of computing the constraints initially renders the evaluation method less efficient. This cost is amortized when verifying a GRN-individualby constraint evaluation is faster than by execution. In the experimental section, we compare the overall performance of the two approaches on a number of GRNs from literature.
6 Experimental results
We ran our tool on a set of GRNs from literature.
We chose eight GRN topologies as benchmarks for our tool. The benchmarks are presented in Fig. 3. The first five of the GRN topologies are collected from [8], on which we check for bistability properties, namely persistence of the initial states for which a partition of the genes is on and another partition of the genes is off. On the three osc3, osc5, and osc7 GRN topologies, we check for the oscillatory behavior. On the final osc25 we check for a valid property. The results of all experiments, but osc25, are presented in Fig. 4. We comment on the results of osc25 at the end of this section.
The comparison in performance when mutational robustness is statistically estimated, and a property check is performed either by evaluation, or by execution (see Sect. 4.1 for the description of the two methods). The bar (top-left) shows the ratio of average times needed to verify the property of one sampled GRN-individual. For example, for osc7, the performance of evaluation method is more than three times faster. The other graphs show how the robustness computation time depends on the total number of sampled GRNs (in order to obtain robustness and to estimate the precision, we computed the mean of 100 experiments, each containing a number of samples ranging from \(10^3\) to \(10^6\)). The graph is shown in log-log scale. The non-linear slope of the evaluation method is most notable in examples ncc and osc7, and it is due to the longer time used for compute the constraints
We ran the robustness computation by the evaluation and execution methods (the methods are described in Sect. 4.1). In order to obtain robustness and to estimate the precision, we computed the mean of 100 experiments, each containing a number of samples ranging from \(10^3\) to \(10^6\). The total computation time in the execution methods linearly depends on the number of samples used. The total computation time in the evaluation method depends linearly on the number of samples, but initially needs time to compute the constraints. Technically, the time needed to compute robustness by execution method is \(t_{ex} = k_{ex}p\), and the time needed to compute robustness by evaluation approach \(t_{ev} = k_{ev}p+t_{c}\), where p represents the total number of samples used, \(t_c\) is the time to compute the constraints, and \(k_{ex}\) (resp. \(k_{ev}\)) is the time needed to verify the property by evaluation (resp. execution). We used linear regression to estimate the parameters \(k_{ex}\) and \(k_{ev}\), and we present the ratio \(\frac{k_{ex}}{k_{ev}}\) in top-left position of Fig. 4. The results indicate that on six out of eight tested networks, evaluation is more efficient than execution. For some networks, such as osc7, the time for computing the constraints is large, and the gain in performance becomes visible only once the number of samples is larger than \(10^6\). On the other hand, for the networks qi and ncc performance are worse, namely evaluating the constraints is more expensive than finding a counterexample for the property by simulation. In fact, due to their high connectivity, the produced constraints is very big, with respect to the number of possible simulations, as the first is worse case exponential in the number of regulatory relations and the second is worse case exponential in the number of genes.
The network osc25 has been designed to demonstrate the drastic advantage of our approach on a network with 25 genes and for a property with robustness value 1. The model checking approach has a precomputation time of about 3.5 s, and an evaluation time of about 0.95 s for \(10^6\) samples. The simulation approach times out with any number of samples. The reason is that the property is valid, hence the solver does not find any counterexample. The resulting LDD will consist of the node 1 only, hence every sample is evaluated in constant time. On the other hand, as the simulator cannot test for the validity of the property in advance, it has to simulate the network for each out of \(2^{25}\) initial states. The osc25 example shows that the strength of our method stands in its logic engine, and that it is very well-suited for networks that are likely to be robust, as its approach consists of searching for and enumerating counter examples.
This experimental evaluations shows that our method is preferrable to the simulation method when networks are sparse and when logic reasoning can play a role in reducing the computational effort.
7 GRN-populationaccording to a mutation model
In this Section, we first present the mutation model without selection, which defines the GRN-population we use in our experimental evaluation. Then we show another, more realistic mutation model with selection, which accounts for evolutionary pressure towards a given property.
Genetic mutations refer to events of changing base pairs in the DNA sequence of the genes and they may disturb the regular functioning of the host cell. Such mutations affect the result of the weight function \(w \in {W}\), inducing a range defined by the GRN space.
Evolutionary biologists are interested in how a population of cells evolves over generations, and, more specifically, in a distribution over phenotypes for an extended number of generations. In our model of GRN-population \(\mathcal {Z}=(T,\pi )\), the distribution \(\pi \) represents such limiting distribution over the phenotypes \(T\). Depending on whether population is subject to evolutionary pressure selecting for some property, two variants of GRN-population arise.
In the following, we first show a model of mutation, and then how the distribution \(\pi \) is derived in both the model without selection and in the model with selection.
7.1 Mutation model
Each gene, a part of DNA which can be transcribed to a protein, is said to be active when the protein encoded by \(g\) is present in the cell. The transcription process is initiated when a transcription factor binds to the promoter region of gene \(g\). A mutation in the promoter region may affect the binding affinity to the transcription factor, and, consequently, that gene’s weight; We assume here that the maximal weight of gene \(g\), that is, \(w(g)\), is achieved for a single sequence of nucleotides, and that it will linearly decrease with the number of mutated nucleotides (where ‘mutated’ refers to being different to the sequence with maximal weight).
A possible way of interpreting the mutation model used in this work is the following. Imagine an experiment which starts with a population of cells, each having a promoter of gene \(g\) in configuration \(\mathbf {a}_0=(a_1,\ldots ,a_{l})\in \{\mathtt {A},\mathtt {T},\mathtt {C},\mathtt {G}\}^{l}\), that is some sequence of \(l\) nucleotides. A mutation in the promoter region may affect the binding affinity to the transcription factor, and, consequently, the gene expression level; We assume that the maximal weight \(w\) is achieved for a single sequence of nucleotides, \({\mathbf {a}}\), and that it will linearly decrease with the increasing number of mis-matching nucleotides. This is clearly an oversimplification, since different mutations at the same site will have different effects in the binding energy and not all sites contribute in the same way to the total binding energy. However, it correlates with what is seen experimentally, where it is generally found that there is one “preferred” sequence, and mutations from that sequence decrease the total binding energy. As such, this assumption simplifies the modelling immensely without compromising too much of the biological detail.
We assume discrete generations and that mutations happen only during replication. When the DNA is passed from the mother to the daughter cell, a nucleotide \(a_i\) can mutate to a different value with probability p, and, consequently, it can remain the same with probability \(1-p\). Furthermore, we assume that the mutations occur only in the promoter region of genes and that the mutation events are independent within the whole genome, and independent of the history of mutations, as is typically assumed in biology.
7.1.1 Modeling mutations in a nucleotide
The mutations of a single nucleotide over generations follow a discrete-time Markov chain (DTMC), illustrated in Fig. 5a. When the DNA is passed from the mother to the daughter cell, a ‘correct’ nucleotide (in figure it is the \(\mathtt {A}\)) can mutate to each different value (\(\mathtt {T}\), \(\mathtt {C}\) or \(\mathtt {G}\)) with some probability. In the model in Fig. 5a, the probability of each possible mutation is \(\frac{p}{3}\), and hence, the probability of retaining the same nucleotide is \(1-p\). In Fig. 5b, there is a process where all mutated states are lumped together—the probability to get to the ‘correct’ nucleotide is equal to \(\frac{p}{3}\), and to remain mutated is therefore \((1-\frac{p}{3})\). We will refer to the general probabilities of the lumped process with a matrix
with the intuition 0 being the non-mutated state and 1 the mutated state. Let \(X_n^i\in \{\mathbf {0},\mathbf {1}\}\) be a process (DTMC) reporting whether the i-th nucleotide is in its ‘correct’ configuration, or mutated configuration at n-th generation. The number \(P(X_n^i=\mathbf {1})\) can be interpreted also as that the fraction of mutated i-th nucleotides observed in the population at generation n. Notably, for the values shown in Fig. 5b, the stationary distribution of \(X_n^i\) is (0.75, 0.25), independently of the probability of a single mutation p.
7.1.2 Modeling mutations for a single gene
Let us assume \(l\) to be the length of the DNA binding region of a geneFootnote 2 \(g\), and \(P^{id}\) to specify the probabilities of single point mutations occurring in it. Moreover, we assume that the maximal weight of gene \(g\), i.e. \(w(g)\), is achieved for a single sequence of nucleotides, and that the weight will linearly decrease with the number of mutated nucleotides (where ‘mutated’ refers to being different to the sequence achieving the maximal weight). Therefore, if k out of \(l\) nucleotides in \(g\) are mutated, the weight of \(g\) becomes \(w(g)(1-\frac{k}{l})\).
If the whole promoter sequence of one gene is modelled by a string \(\mathbf {a}\in \{\mathtt {A},\mathtt {T},\mathtt {C},\mathtt {G}\}^{l}\), its changes over generations are captured by an l-dimensional random process of type \((X_n^1,\ldots ,X_n^l)(\mathbf {a})\in \{\mathbf {0},\mathbf {1}\}^l\). Mutation events \(X_n^1\), \(X_n^2\),..., \(X_n^l\) are assumed to happen independently across the genome, and independently of the history of mutations. Then, a random process \(M_n:=X_n^1+\cdots +X_n^l\), such that \(M_n=k\in \{0,\ldots ,l\}\), denotes that the configuration at generation n differs from the optimal configuration in exactly k points. The following lemma defines the values of the transition matrix of the process \(\{M_n\}\).
Lemma 2
The process \(\{M_n\}\) is a DTMC, with transition probabilities \(P(M_{n+1}=j\mid M_n=i) = T({i,j})\), where \(T: 0..l\times 0..l\rightarrow [0,1]\) amounts to:
Proof
It suffices to observe that u represents the number of mutated nucleotides which remain mutated at time \((n+1)\), and \((j-u)\) is the number of unmated nucleotides which become mutated at time \((n+1)\). The existence and convergence of the stationary trivially follows from that \(\{M_n\}\) is regular (irreducible and aperiodic). Each process \(\{X_n^i\}\) at a stationary behaves as a Bernoulli process, with probability of being mutated equal to \(\beta =\lim _{n\rightarrow \infty } P(X_n^i=1)\), and a probability of remaining un-mutated \(1-\beta \). The claim follows as the sum of l independent Bernoulli processes is binomially distributed. The special case follows because matrix \(\hat{P}^{id}\) has a unique stationary distribution (0.25, 0.75) (denoting by a and b its coordinates, we obtain equations \(a(1-p)+b\frac{p}{3}=a\) and \(ap+b(1-\frac{p}{3})=b\), which can be satisfied only if \(a=\frac{b}{3}\)).
Moreover, \(\{M_n\}\) converges to a unique stationary distribution, which is a binomial, with success probability \(\beta =\lim _{n\rightarrow \infty } P(X_n^i=\mathbf {1})\). In a special case  , the stationary distribution is \(\beta =\frac{3}{4}\), independently of the value of p.
, the stationary distribution is \(\beta =\frac{3}{4}\), independently of the value of p.
The special case of matrix \(T\) for \(l=2\) is illustrated in Fig. 6.
The transition matrix for the evolutionary process of one gene with two nucleotides. The transition probabilities are computed based on the assumption that the single nucleotide mutations happen independently across the genome: for example, the transition from zero to two mutation is equal to \(p_{01}^2\), because it occurs iff both nucleotides transition from a correct to a mutated state
7.1.3 Modeling mutations in a GRN
We assume mutations happen independently across the genome, therefore if the genome is in the configuration \(\mathbf k =(k_1,\ldots ,k_d)\), the probability that the next generation will be in the configuration \(\mathbf k '=(k_1',\ldots ,k_d')\) will be a product of transition probabilities from \(k_i\) to \(k_i'\), for \(i=1,\ldots ,d\). In other words, each sequence \(\mathbf k =(k_1,\ldots ,k_d)\in 0..l_1\times \cdots \times 0..l_{d}\) defines one weight function \(w_\mathbf{k }\), with \(w_\mathbf{k }(g_i)=w(g_i)(1-\frac{k_i}{l_i})\). The possible weight configurations of a GRN are defined accordingly.
Definition 8
(GRN space due to mutation model) Let \(l_1,\ldots ,l_{d}\) denote the lengths of respective genes. The GRN space due to mutation model is induced by
and the probability of exhibiting weight function \(w_\mathbf{k '}\) in the next generation, given that the weight function in the current generation is \(w_\mathbf{k }\), is given by
where \(T\) is defined in (5).
7.2 GRN-populationin a model without selection
Definition 9
The GRN-population \(\mathcal {Z}=(T,\pi )\) is defined by a model without selection, if \(T\) is a GRN space over the weight functions defined in (6), and \(\pi :{W}\rightarrow [0,1]\) is a limit of a sequence of distributions \(\pi _0,\pi _1,\pi _2,\ldots \), such that
Equation (7) tells that the probability of observing weight w in generation \(i+1\) equals the total probability of mutating from any possible weight \(w'\) in generation i to weight w.
Lemma 3
The sequence defined in (7) converges to a unique distribution \(\pi (w_\mathbf{k }) = \prod _{i=1}^d{l_i\atopwithdelims ()k_i}\beta _i^{k_i}(1-\beta _i)^{d_i-k_i}\), where \(\beta _i = \lim _{n\rightarrow \infty } P(X_n^i=1)\).
Proof
Let \({\mathbf {T}}\) be a matrix notation for transition function \(\mathcal{T}\), given some fixed ordering among the weight function. The matrix \({\mathbf {T}}\) is obviously regular, because, from (5), each two states have a non-zero transition probability.
7.3 GRN-populationin a model with selection
In a model with selection, upon mutations occur, only the individuals satisfying the selection property survive. However, the total population size remains constant, meaning that, even though a number of individuals dies, those individuals who meet the property reproduce more, that is, the nature selects for the individuals satisfying the property. We take the selection property to be equal to the property we check robustness for. In this context, the robustness is the ratio of surviving individuals upon mutations occur on the long-term.
With abuse of notation, let \(\varphi ({W})\subseteq {W}\) denote the subset of surviving weight configurations: \(\varphi ({W}) = \{w\in {W}\mid \varphi (w) = 1\}\).
Definition 10
The GRN-population \(\mathcal {Z}=(T,\pi )\) is defined by a model with selection with respect to the selection property expressed in LTL \(\varphi \), if \(T\) is a GRN space over the weight functions defined in (6), and \(\pi :{W}\rightarrow [0,1]\) is a limit of a sequence of distributions \(\pi _0,\pi _1,\pi _2,\ldots \), such that
The probability of seeing weight w in generation \(i+1\) is the probability of transition from any \(w'\) in generation i, but first normalised over all surviving configurations \(w''\). The above definition is inspired by a similar definition presented in [11], i.e., the probability of a singly mutated GRN satisfying the property.
The next theorem states how to compute the robustness in the model with selection. See Fig. 6 for illustration.
Theorem 2
Let \(\mathbf {T}\in [0,1]^{|(0..l_1\times \cdots \times 0..l_{d})|^2}\) be the matrix encoding the transition probability \(\mathcal{T}\) between two mutated weights, and let \(\varvec{\pi }\) be the (row) vector notation for the converging distribution function \(\pi \). Let \(\tilde{\mathbf {T}}\in [0,1]^{|\varphi ({W})|\times |\varphi ({W})|}\) (resp. \(\tilde{\varvec{\pi }}\)) be the restriction of \(\mathbf {T}\) (resp. \(\varvec{\pi }\)) to the components in \(\varphi ({W})\). Then, \(\tilde{\varvec{\pi }}\) is the eigenvector for \(\tilde{\mathbf {T}}\), with the eigenvalue \(\Vert \tilde{\varvec{\pi }}\tilde{\mathbf {T}}\Vert \). Moreover, this eigenvalue is exactly robustness, \(\varphi ( \mathcal {Z})\).
Proof
Denote by \(\Vert \cdot \Vert \) the 1-norm (sum of vector elements). The definition of update of the probability distribution as shown in Dfn. 10, written in matrix notation amounts to:
The stationary distribution \(\tilde{\varvec{\pi }}\) satisfies \(\tilde{\varvec{\pi }}\Vert \tilde{\varvec{\pi }} \tilde{\mathbf {T}}\Vert =\tilde{\varvec{\pi }} \tilde{\mathbf {T}}\), and is therefore an eigenvector for \(\tilde{\mathbf {T}}\). Since matrix \(\tilde{\mathbf {T}}\) is regular, there exist \(k>0\) such that \(\tilde{\mathbf {T}}^k\) has all strictly positive entries. By the Perron-Frobenius theorem (4), \(\tilde{\mathbf {T}}^k\) has a dominant eigenvalue with multiplicity one, which corresponds to a unique non-negative eigenvector space, scaled to \(\tilde{\varvec{\pi }}\). The convergence follows from Theorem 5.
Finally, \(\Vert \tilde{\varvec{\pi }} \tilde{\mathbf {T}}\Vert \) is the matrix form of \(\varphi ( \mathcal {Z})\) in Dfn. 7, which proves the second part of the claim.
Finally, we show that robustness measure preserves monotonicity in the sense that larger properties imply larger robustness in both model with and without selection.
Theorem 3
Let \(\varphi \) and \(\varphi '\) be two properties such that for all \(w\in {W}\), \(\varphi (w) \Rightarrow \varphi '(w)\), that is, the parameter space where \(\varphi \) holds is fully contained in the space where \(\varphi '\) holds. Then, \(\varphi ( \mathcal {Z})\le \varphi '(\mathcal {Z})\), that is, the robustness with respect to property \(\varphi \) is not larger than the robustness with respect to property \(\varphi '\), both in model without selection and model with selection with respect to property \(\varphi \) (resp. \(\varphi '\)).
Proof
In case of model without selection, the claim trivially holds. For model with selection, by Theorem 2, it suffices to show that the eigenvalue of \(\tilde{\mathbf {T}}(\varphi )\) is not larger than the eigenvalue of \(\tilde{\mathbf {T}}(\varphi ')\). By the assumption, \(\tilde{\mathbf {T}}(\varphi )\) can be obtained from \(\tilde{\mathbf {T}}(\varphi ')\) by deleting rows and columns corresponding to those states that do not satisfy \(\varphi \). By instantiating Gelfand’s formula for the 1-norm, the claim follows.
The following terminology and results can be found in any standard linear algebra textbook.
Definition 11
A matrix \(M\in {\mathbf R}^{m\times n}\) is called positive (resp. non-negative), written \(M>0\) (resp. \(M\ge 0\)), if all entries of M are strictly positive (resp. non-negative).
Definition 12
A square matrix \(M\in {\mathbf R}^{n\times n}\) is regular, if there exists \(k>0\), such that \(M^{k}\ge 0\).
Theorem 4
(Perron–Frobenious) Let M be a square, positive matrix. Then,
-
1.
M has an eigenvalue \(\hat{\lambda }\in {\mathbf R}_{>0}\), such that for all other eigenvalues \(\lambda \), we have \(|\lambda |<\hat{\lambda }\),
-
2.
the right- and left-eigenvectors associated to eigenvalue \(\hat{\lambda }\) are the only eigenvectors with all real, positive entries.
-
3.
the eigenvalue \(\hat{\lambda }\) has multiplicity one.
Proof
(Sketch) We only show the proof for (1). If M has a spectral radius \(\rho (M)\), then \(M'=\frac{M}{\rho (M)}\) has an eigenvector on the unit circle, and all other eigenvalues of \(M'\) are smaller or equal to 1. Assume \(r=\rho (M')\ne 1\). Then, there exists \(m\in {\mathbb N}\), such that \(Re(r^m)<0\). Notice that the matrix \({M'}^m-\epsilon I\) has all positive entries for some small enough \(\epsilon >0\). Moreover, by Gelfand’s formula (\(\lim _{k\rightarrow \infty } \Vert A^k\Vert ^{1/k}=\rho (A)\) for any matrix norm \(\Vert \cdot \Vert \)), it follows that \(\rho ({M'}^m-\epsilon I)\le \rho ({M'}^m)\le {\rho (M')}^m=1\). On the other hand, since \(({M'}^m-\epsilon I)v=(r^m-\epsilon )v\) for any vector v, it follows that \(r^m-\epsilon \) is an eigenvalue for \({M'}^m-\epsilon I\), and consequently \(\rho ({M'}^m-\epsilon I)>\Vert r^m-\epsilon \Vert =1\). Contradiction.
Hence the spectral radius of M is achieved for a positive real eigenvalue.
Theorem 5
Let M be a square, non-negative, regular matrix. If v is the unit, left eigenvector for dominant eigenvalue \(\hat{\lambda }\) with norm 1, that is, \(vM=\hat{\lambda }v\), then for all \(v_0\in [0,1]^n\), such that \(|v_0|=1\), \(v_0\) has a non-zero component in the direction of the dominant eigenvector, and the sequence
where \(g(w) := \frac{wM}{|wM|}\), converges to v.
Proof
(Sketch) As M is non-negative and regular, there exists \(m>0\) such that \(g^m(v_0)>0\). The convergence can be shown from the Jordan canonical form and by subsequently applying the power iteration approach. Let \(v_0\) be the initial distribution, and let \(M=VJV^{-1}\) be the Jordan canonical form of M. The vector \(v_0\) can be written as a linear combination of the rows of \(V^{-1}\) (generalized right eigenvectors): \(v_0=c_1v_1+\cdots +c_nv_n\), where \(c_1\ne 0\) is non-negative eigenvector \(v_1\) corresponding to the dominant eigenvalue.
Lemma 4
A regular stochastic square matrix has a unique stationary distribution and it converges to it.
Proof
Since all row sums are equal to 1, the column vector of only ones is an eigenvector, and the corresponding eigenvalue is 1. Hence, there exists a positive left eigenvector \(\pi \) for eigenvalue 1. Then, \(\nu =\frac{\pi }{|\pi |}\) is a stationary distribution. The proof of uniqueness and convergence follow as in the proof for Theorems 4 and 5.
8 Conclusion and discussion
In this paper, we pursued formal analysis of Wagner’s GRN model, which allows symbolic reasoning about the behavior of GRNs under parameter perturbations. More precisely, for a given space of GRNs and a property specified in LTL, we have synthesized the space of parameters for which the concrete, individual GRN from a given space satisfies the property. The resulting space of parameters is represented by complex linear inequalities. In our analysis, we have encoded a bounded model-checking search into a satisfiability problem, and we used efficient SMT solvers to find the desired constraints. We demonstrated that these constraints can be used to efficiently compute the mutational robustness of populations of GRNs. Our results have shown the cases in which the computation can be three times faster than the standard (simulation) techniques employed in computational biology.
While computing mutational robustness is one of the applications of our synthesized constraints, the constraints allow to efficiently answer many other questions that are very difficult or impossible to answer by executing the sampled GRNs. In our future work, we aim to work on further applications of our method, such as parameter sensitivity analysis for Wagner’s model. Moreover, we plan to work on the method for exact computation of robustness by applying point counting algorithms [5].
The Wagner’s model of GRN is maybe the simplest dynamical model of a GRN—there are many ways to add expressiveness to it: for example, by incorporating multi-state expression level of genes, non-determinism, asynchronous updates, stochasticity. We are planning to study these variations and chart the territory of applicability of our method.
Notes
The artifact is available at http://pub.ist.ac.at/~mgiacobbe/grnmc.tar.gz.
More precisely the length of the promoter of gene.
References
Azevedo, R.B.R., Lohaus, R., Srinivasan, S., Dang, K.K., Burch, C.L.: Sexual reproduction selects for robustness and negative epistasis in artificial gene networks. Nature 440(7080), 87–90 (2006)
Baier, C., Katoen, J.-P.: Principles of Model Checking. The MIT Press, Cambridge, Massachusetts, London (2008)
Barrett, C., Deters, M., de Moura, L., Oliveras, A., Stump, A.: 6 years of SMT-COMP. J. Autom. Reason. 50(3), 243–277 (2013)
Barrett, C.W., Sebastiani, R., Seshia, S.A., Tinelli, C.: Satisfiability modulo theories. Handb. Satisf. 185, 825–885 (2009)
Barvinok, A., Pommersheim, J.E.: An algorithmic theory of lattice points in polyhedra. New Perspect. Algebraic Combin. 38, 91–147 (1999)
Batt, G., Yordanov, B., Weiss, R., Belta, C.: Robustness analysis and tuning of synthetic gene networks. Bioinformatics 23(18), 2415–2422 (2007)
Biere, A., Cimatti, A., Clarke, E.M., Strichman, O., Zhu, Y.: Bounded model checking. Adv. Comput. 58, 117–148 (2003)
Cardelli, L.: Morphisms of reaction networks that couple structure to function. BMC Syst. Bio. 8(1), 84 (2014)
Cardelli, L., Csikász-Nagy, A.: The cell cycle switch computes approximate majority. Sci. Rep. 2, 1–9 (2012)
Chaki, S., Gurfinkel, A., Strichman, O.: Decision diagrams for linear arithmetic. In: Formal Methods in Computer-Aided Design, 2009. FMCAD 2009, pp. 53–60. IEEE (2009)
Ciliberti, S., Martin, O.C., Wagner, A.: Robustness can evolve gradually in complex regulatory gene networks with varying topology. PLoS Comput. Biol. 3(2), 164–173 (2007)
Danos, V., Laneve, C.: Formal molecular biology. Theor. Comput. Sci. 325(1), 69–110 (2004)
de Moura, L.M., Bjørner, N.: Z3: an efficient SMT solver. In: TACAS (2008)
Elowitz, M.B., Leibler, S.: A synthetic oscillatory network of transcriptional regulators. Nature 403(6767), 335–338 (2000)
Fisher, J., Henzinger, T.A.: Executable cell biology. Nature Biotechnol. 25(11), 1239–1249 (2007)
Gardner, T.S., Cantor, C.R., Collins, J.J.: Construction of a genetic toggle switch in Escherichia coli. Nature 403(6767), 339–342 (2000)
Giacobbe, M., Guet, C.C., Gupta, A., Henzinger, T.A., Paixao, T., Petrov, T.: Model checking gene regulatory networks. In: Baier, C., Tinelli, C. (eds.) Tools and Algorithms for the Construction and Analysis of Systems, pp. 469–483. Springer, Berlin, Heidelberg (2015)
Hafner, M., Petrov, T., Lu, J., Koeppl, H.: Rational design of robust biomolecular circuits: from specification to parameters. In: Koeppl, H., Setti, G., di Bernardo, M., Densmore, D. (eds.) Design and Analysis of Biomolecular Circuits, pp. 253–279. Springer, New York (2011)
Jha, S.K., Clarke, E.M., Langmead, C.J., Legay, A., Platzer, A., Zuliani, P.: A Bayesian approach to model checking biological systems. In: Degano, P., Gorrieri, R. (eds.) Computational Methods in Systems Biology, pp. 218–234. Springer, Berlin, Heidelberg (2009)
Kwiatkowska, M., Norman, G., Parker, D.: Using probabilistic model checking in systems biology. ACM SIGMETRICS Perform. Eval. Rev. 35(4), 14–21 (2008)
Lahiri, S.K., Nieuwenhuis, R., Oliveras, A.: SMT techniques for fast predicate abstraction. In: Ball, T., Jones, R.B. (eds.) Computer Aided Verification, pp. 424–437. Springer, Berlin, Heidelberg (2006)
Rizk, A., Batt, G., Fages, F., Soliman, S.: A general computational method for robustness analysis with applications to synthetic gene networks. Bioinformatics 25(12), i169–i178 (2009)
Schlitt, T., Brazma, A.: Current approaches to gene regulatory network modelling. BMC Bioinform. 8(Suppl 6), S9 (2007)
Wagner, A.: Does evolutionary plasticity evolve? Evolution 50(3), 1008–1023 (1996)
Yordanov, B., Wintersteiger, C.M., Hamadi, Y., Kugler, H.: SMT-based analysis of biological computation. In: Brat, G., Rungta, N., Venet, A. (eds.) NASA Formal Methods, pp. 78–92. Springer, Berlin, Heidelberg (2013)
Zhang, L., Madigan, C.F., Moskewicz, M.H., Malik, S.: Efficient conflict driven learning in a boolean satisfiability solver. In: Proceedings of the 2001 IEEE/ACM International Conference on Computer-Aided Design, pp. 279–285. IEEE Press (2001)
Acknowledgments
Open access funding provided by Institute of Science and Technology (IST Austria).
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by the European Research Council (ERC) under Grant 267989 (QUAREM), the Austrian Science Fund (FWF) under Grants S11402-N23 (RiSE) and Z211-N23 (Wittgenstein Award), the European Union’s SAGE Grant Agreement No. 618091, ERC Advanced Grant ERC-2009-AdG-250152, the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme (FP7/2007-2013) under REA Grant Agreement No. 291734, and the SNSF Advanced Postdoc.Mobility Fellowship, the Grant Number P300P2_161067.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Giacobbe, M., Guet, C.C., Gupta, A. et al. Model checking the evolution of gene regulatory networks. Acta Informatica 54, 765–787 (2017). https://doi.org/10.1007/s00236-016-0278-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-016-0278-x






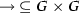 is the activation relation such that
is the activation relation such that 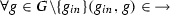 and
and 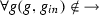 ,
,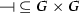 is the repression relation such that
is the repression relation such that 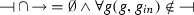 ,
, is the maximum value of an activation/repression,
is the maximum value of an activation/repression,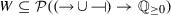 assigns a set of possible weight functions to each activation/inhibition relation, so that
assigns a set of possible weight functions to each activation/inhibition relation, so that 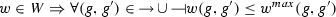 .
.



