Abstract
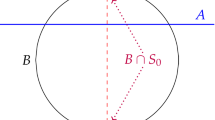
We study the relationship between a convex body \({K\subset \mathbb{R}^{n}}\) and the convex floating body K δ inside K. Our results complement recent work of Grigoris Paouris and Elisabeth Werner.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Ball K.: Logarithmically concave functions and sections of convex sets in \({\mathbb{R}^{n}}\) . Studia Math. 88, 69–84 (1988)
K. Ball, An elementary introduction to modern convex geometry, Flavors of Geometry, MSRI Publications 31, 1997.
Bárány I., Larman D.: Convex bodies, economic cap coverings, random polytopes. Mathematika 35, 274–291 (1988)
Bobkov S.: Isoperimetric and analytic inequalities for log-concave probability measures. Ann. Probab. 27, 1903–1921 (1999)
Borell C.: Convex set functions in d-space. Period. Math. Hungar. 6, 111–136 (1975)
Bourgain J.: On high-dimensional maximal functions associated to convex bodies. Amer. J. Math. 108, 1467–1476 (1986)
J. Bourgain, On the distribution of polynomials on high-dimensional convex sets, Geometric aspects of functional analysis, (1989–1990), 127–137, Lecture Notes in Math. 1469, Springer, Berlin (1991)
Fradelizi M.: Hyperplane sections of convex bodies in isotropic position. Beiträge Algebra Geom. 40, 163–183 (1999)
D. Fresen, A multivariate Gnedenko law of large numbers, arXiv:1101.4887
Giannopoulos A., Paouris G., Valettas P.: On the existence of subgaussian directions for log-concave measures. Contemporary Mathematics 545, 103–122 (2011)
Hensley D.: Slicing convex bodies-bounds for slice area in terms of the body’s covariance. Proc. Amer. Math. Soc. 79, 619–625 (1980)
Klartag B.: A central limit theorem for convex sets. Invent. Math. 168, 91–131 (2007)
Klartag B.: On convex perturbations with a bounded isotropic constant. Geom. Funct. Anal. 16, 1274–1290 (2006)
Klartag B., Milman V.: Geometry of log-concave functions and measures. Geom. Dedicata 112, 169–182 (2005)
Lovász L., Vempala S.: The geometry of logconcave functions and sampling algorithms. Random Structures Algorithms 30, 307–358 (2007)
V. Milman and A. Pajor, Isotropic position and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space. Geometric aspects of functional analysis, Israel seminar (1987-1988), Lecture Notes in Math. 1376, Springer-Verlag, Berlin 64–104 (1989)
G. Paouris and E. Werner, Relative entropy of cone measures and L p centroid bodies, Proc. London Math. Soc. pdr030 first published online August 31, 2011 doi:10.1112/plms/pdr030
Pisier G.: The volume of convex bodies and Banach space geometry, Cambridge Tracts in Mathematics 94. Cambridge University Press, Cambridge (1989)
Schütt C.: On the affine surface area. Proc. Amer. Math. Soc. 118, 1213–1218 (1993)
Schütt C.: The convex floating body and polyhedral approximation. Israel J. Math. 73, 65–77 (1991)
Schütt C., Werner E.: The convex floating body. Math. Scand. 66, 275–290 (1990)
Vu V.: Sharp concentration of random polytopes. Geom. and Funct. Anal. 15, 1284–1318 (2005)
Author information
Authors and Affiliations
Corresponding author
Additional information
To my dear sister Anna
Many thanks to Sergey Bobkov, Jill Fresen, John Fresen, Nigel Kalton, Alexander Koldobsky, Elizabeth Meckes, Mark Meckes, Mathieu Meyer, Mark Rudelson and Elisabeth Werner for their comments and/or support, as well as the anonymous referee for making valuable suggestions, including several appropriate references.
Rights and permissions
About this article
Cite this article
Fresen, D. The floating body and the hyperplane conjecture. Arch. Math. 98, 389–397 (2012). https://doi.org/10.1007/s00013-012-0365-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00013-012-0365-3