Abstract
We introduce the notion of a continuous verifiable delay function (cVDF): a function g which is (a) iteratively sequential—meaning that evaluating the iteration \(g^{(t)}\) of g (on a random input) takes time roughly t times the time to evaluate g, even with many parallel processors, and (b) (iteratively) verifiable—the output of \(g^{(t)}\) can be efficiently verified (in time that is essentially independent of t). In other words, the iterated function \(g^{(t)}\) is a verifiable delay function (VDF) (Boneh et al., CRYPTO ’18), having the property that intermediate steps of the computation (i.e., \(g^{(t')}\) for \(t'<t\)) are publicly and continuously verifiable.
We demonstrate that cVDFs have intriguing applications: (a) they can be used to construct \(\textit{public randomness beacons}\) that only require an initial random seed (and no further unpredictable sources of randomness), (b) enable \(\textit{outsourceable VDFs}\) where any part of the VDF computation can be verifiably outsourced, and (c) have deep complexity-theoretic consequences: in particular, they imply the existence of depth-robust moderately-hard Nash equilibrium problem instances, i.e. instances that can be solved in polynomial time yet require a high sequential running time.
Our main result is the construction of a cVDF based on the repeated squaring assumption and the soundness of the Fiat-Shamir (FS) heuristic for \(\textit{constant-round proofs}\). We highlight that when viewed as a (plain) VDF, our construction requires a weaker FS assumption than previous ones (earlier constructions require the FS heuristic for either super-logarithmic round proofs, or for arguments).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
A fundamental computational task is to simulate “real time” via computation. This was first suggested by Rabin [42] in 1983, who introduced a notion called randomness beacon to describe an ideal functionality that publishes unpredictable and independent random values at fixed intervals. This concept has received a substantial amount of attention since its introduction, and even more so in recent years due to its many applications to more efficient and reliable consensus protocols in the context of blockchain technologies.
One natural approach, which is the focus of this work, is to implement a randomness beacon by using an iteratively sequential function.Footnote 1 An iteratively sequential function g inherently takes some time \(\ell \) to compute and has the property that there are no shortcuts to compute sequential iterations of it. That is, computing the t-wise composition of g for any t should take roughly time \(t \cdot \ell \), even with parallelism. Using an iteratively sequential function g with an initial seed x, we can construct a randomness beacon where the output at interval t is computed as the hash of
After \(t \cdot \ell \) time has elapsed (at which point we know the first t values), the beacon’s output should be unpredictable sufficiently far in the future.Footnote 2 The original candidate iteratively sequential function is based on (repeated) squaring in a finite group of unknown order [13, 43]. It is also conjectured that any secure hash function (such as SHA-256) gives an iteratively sequential function; this was suggested in [30] and indeed, as shown in [36], a random oracle is iteratively sequential.
Continuous VDFs. The downside of using an iteratively sequential function as a randomness beacon is that to verify the current value of the beacon, one needs to recompute its entire history which is time consuming by definition. In particular, a party that joins late will never be able to catch up. Rather, we would like the output at each step to be both publicly and efficiently verifiable. It is also desirable for the randomness beacon to be generated without any private state so that anyone can compute it, meaning that each step can be computed based solely on the output of the preceding step. Indeed, if we have an iteratively sequential function that is also (iteratively) verifiable—in the sense that one can efficiently verify the output of \(g^{(t)}(x)\) in time \(\mathrm {polylog} (t)\)—then such a function could be used to obtain a public randomness beacon. In this paper, we introduce and construct such a function and refer to it as a continuous verifiable delay function (cVDF). As the name suggests, it can be viewed as enabling continuous evaluation and verification of a verifiable delay function (VDF) [10] as we describe shortly.Footnote 3
Continuous VDFs are related to many previously studied time-based primitives. One classical construction is the time-lock puzzle of Rivest, Shamir, and Wagner [43]. Their construction can be viewed as an iteratively sequential function that is privately verifiable with a trapdoor—unfortunately, this trapdoor not only enables quickly verifying the output of iterations of the function, but in fact also enables quickly computing the iterations. New publicly verifiable time-based primitives have since emerged, including proofs of sequential work (PoSW) [18, 21, 36] and verifiable delay functions (VDF) [10, 11, 23, 40, 45]. While these primitives are enough for many applications, they fall short of implementing a public randomness beacon (on their own). In more detail, a PoSW enables generating a publicly verifiable proof of some computation (rather than a specific function with a unique output) that is guaranteed to have taken a long time. This issue was overcome through the introduction of VDFs [10], which are functions that require some “long” time T to compute (where T is a parameter given to the function), yet the answer to the computation can be efficiently verified given a proof that can be jointly generated with the output (with only small overhead).
In fact, one of the motivating applications for constructing VDFs was to obtain a public randomness beacon. A natural approach toward this goal is to simply iterate the VDF at fixed intervals. However, this construction does not satisfy our desired efficiency for verifiability. In particular, even though the VDF enables fast verification of each invocation, we still need to store all proofs for the intermediate values to verify the final output of the iterated function, and thus the proof size and verification time grow linearly with the number of invocations t. While a recent construction of Wesolowski [45] enables aggregating these intermediate proofs to obtain a single short proof, the verification time still grows linearly with t (in contrast, a cVDF enables continuously iterating a function such that the output of t iterations can be efficiently verified in time essentially independent of t, for any t). While a VDF does not directly give a public randomness beacon, it does, however, enable turning a “high-entropy beacon” (e.g., continuous monitoring of stock market prices) into an unbiased and unpredictable beacon as described in [10]. In contrast, using a cVDF enables dispensing altogether with the high-entropy beacon—we simply need a single initial seed x.
Continuous VDFs are useful not only for randomness beacons, but also for standard applications of VDFs. Consider a scenario where some entity is offering a $5M reward for evaluating a single VDF with time parameter 5 years (i.e., it is supposed to take five years to evaluate it). Alice starts evaluating the VDF, but after two years runs out of money and can no longer continue the computation. Ideally, she would like to sell the work she has completed for $2M. Bob is willing to buy the intermediate state, verify it, and continue the computation. The problem, however, is that there is no way for Bob to verify Alice’s internal state. In contrast, had Alice used a cVDF, she would simply be iterating an iteratively sequential function, and we would directly have the guarantee that at any intermediate state of the computation can be verified and Alice can be compensated for her effort. In other words, cVDF enable verifiably outsourcing VDF computation.
Finally, as we show, cVDFs are intriguing also from a complexity-theoretic point of view. The existence of cVDFs imply that \(\mathsf {PPAD}\) [39] (the class for which the task of finding a Nash equilibrium in a two-party game is complete) is hard—in fact, the existence of cVDFs imply the existence of a relaxed-SVL [5, 15] instance with tight hardness (which yields improved hardness results also for \(\mathsf {PPAD}\)). Additionally, the existence of cVDFs imply that there is a constant d such that for large enough c, there is a distribution over Nash equilibrium problem instances of size n that can be solved in time \(n^c\) but cannot be solved in depth \(n^{c/d}\) (and arbitrary polynomial size)—that is, the existence of “easy” Nash equilibrium problem instances that requires high sequential running time. In other words, cVDFs imply that it is possible to sample “moderately-hard” Nash equilibrium problem instances that require a large time to solve, even with many parallel processors.
1.1 Our Results
Our main result is the construction of a cVDF based on the repeated squaring assumption in a finite group of unknown order and a variant of the Fiat-Shamir (FS) heuristic for constant-round proof systems. Informally, the iteratively sequential property of our construction comes from the repeated squaring assumption which says that squaring in this setting is an iteratively sequential function. We use the Fiat-Shamir assumption to obtain the continuous verifiability property of our construction. More precisely, we apply the Fiat-Shamir heuristic on a constant-round proof system where the verifier may be inefficient. We note that by the classic results of [26] this holds in the random oracle model.
Theorem 1.1
(Informal, see Corollary 6.3). Under the repeated squaring assumption and the Fiat-Shamir assumption for constant-round proof systems with inefficient verifiers, there exists a cVDF.
We remark that to obtain a plain VDF we only need the “standard” Fiat-Shamir assumption for constant-round proof systems (with efficient verifiers).
A cVDF readily gives a public randomness beacon. As discussed above, the notions of cVDFs and public randomness beacons are closely related. The main difference between the two is that the output of a randomness beacon should not only be unpredictable before a certain time, but should also be indistinguishable from random. Thus, we obtain our public randomness beacon by simply “hashing” the output of the cVDF. We show that this indeed gives a public randomness beacon by performing the hashing using a pseudo-random generators (PRGs) for unpredictable sources (which exist either in the random oracle model or from extremely lossy functions [46]).
Theorem 1.2
(Informal). Assuming the existence of cVDFs and PRGs for unpredictable sources, there exists a public randomness beacon.
Comparison with (Plain) VDFs. The two most related VDF constructions are that of Pietrzak [40] and that of Wesolowski [45], as these are based on repeated squaring. In terms of assumptions, Pietrzak’s protocol [40] assumes the Fiat-Shamir heuristic for a proof system with a super-constant number of rounds and Wesolowski’s [45] assumes the Fiat-Shamir heuristic for a constant-round argument system. It is known that, in general, the Fiat-Shamir heuristic is not true for super-constant round protocols (even in the random oracle modelFootnote 4), and not true for constant-round arguments [6, 27]. As such, both of these constructions rely on somewhat non-standard assumptions. In contrast, our VDF relies only on the Fiat-Shamir heuristic for a constant-round proof system—no counter examples are currently known for such proof systems.
We additionally note that before applying the Fiat-Shamir heuristic (i.e., a VDF in the random oracle model), our VDF satisfies computational uniqueness while Pietrzak’s satisfies statistical uniqueness. He achieves this by working over the group of signed quadratic residues. We note that we can get statistical uniqueness in this setting using the same idea. Lastly, we emphasize that the concrete proof length and verification time are polynomially higher in our case than that of both Pietrzak and Wesolowski. For a detailed comparison of the parameters, see Sect. 2.3.
PPAD Hardness. \(\mathsf {PPAD}\) [39] is an important subclass in \(\mathsf {TFNP}\) [38] (the class of total search problems), most notably known for its complete problem of finding a Nash equilibrium in bimatrix games [14, 19]. Understanding whether \(\mathsf {PPAD}\) contains hard problems is a central open problem and the most common approach for proving hardness was pioneered by Abbot, Kane, and Valiant [5]. They introduced a problem, which [9] termed Sink-of-Verifiable-Line (SVL), and showed that it reduces to End-Of-Line (EOL), a complete problem for \(\mathsf {PPAD}\). In SVL, one has to present a function f that can be iterated and each intermediate value can be efficiently verified, but the output of T iterations (where T is some super-polynomial value, referred to as the length of the “line”) is hard to compute in polynomial time.
In a beautiful recent work, Choudhuri et al. [15] defined the relaxed-Sink-of-Verifiable-Line (rSVL) problem, and showed that it reduces to EOL, as well. rSVL is a generalization of SVL where one is required to find either the output after many iterations (as in SVL) or an off-chain value that verifies. Choudhuri et al. [15] gave a hard rSVL instance assuming the security of the Fiat-Shamir transformation applied to the sum-check protocol [35] (which is a polynomial-round protocol).
The notion of an (r)SVL instance is very related to our notion of a cVDF. The main differences are that a cVDF requires that the gap between the honest computation and the malicious one is tight and that security holds for adversaries that have access to multiple processors running in parallel. As such, the existence of a cVDF (which handles super-polynomially many iterations) directly implies an rSVL instances with “optimal” hardness—namely, one where the number of computational steps required to solve an instance of the problem with a “line” of length T is \((1-\epsilon ) \cdot T\).
Theorem 1.3
(Informal). The existence of a cVDF supporting superpolynomially many iterations implies an optimally-hard rSVL instance (which in turn implies that \(\mathsf {PPAD}\) is hard (on average)).
Theorem 1.1 readily extends to give a cVDF supporting super-polynomially many iterations by making a Fiat-Shamir assumption for \(\omega (1)\)-round proof systems. As a consequence, we get an optimally-hard instance of rSVL based on this Fiat-Shamir assumption for \(\omega (1)\)-round proofsFootnote 5 and the repeated squaring assumption. By following the reductions from rSVL to EOL and to finding a Nash equilibrium, we get (based on the same assumptions) hard \(\mathsf {PPAD}\) and Nash equilibrium instances. We remark that in comparison to the results of Choudhuri et al., we only rely on the Fiat-Shamir assumption for \(\omega (1)\)-round protocols, whereas they rely on it for a polynomial-round, or at the very least an \(\omega (\log n)\)-round proof systems (if additionally assuming that #SAT is sub-exponentially hard). On the other hand, we additionally require a computational assumption–namely, the repeated squaring assumption, whereas they do not.Footnote 6
Our method yields \(\mathsf {PPAD}\) instances satisfying another interesting property: we can generate \(\mathsf {PPAD}\) (and thus Nash equilibrium problem) instances that can be solved in polynomial time, yet they also require a high sequential running time—that is, they are “depth-robust” moderately-hard instances. As far as we know, this gives the first evidence that \(\mathsf {PPAD}\) (and thus Nash equilibrium problems) requires high sequential running time to solve (even for easy instances!).
Theorem 1.4
(Informal). The existence of a cVDF implies a distribution of depth-robust moderately-hard \(\mathsf {PPAD}\) instances. In particular, there exists a constant d such that for all sufficiently large constants c, there is a distribution over Nash equilibrium problem instances of size n that can be solved in time \(n^c\) but cannot be solved in depth \(n^{c/d}\) and arbitrary polynomial time.Footnote 7
Combining Theorems 1.1 and 1.4, we get a depth-robust moderately-hard \(\mathsf {PPAD}\) instance based on the Fiat-Shamir assumption for constant-round proof systems with inefficient verifiers and the repeated squaring assumption.
1.2 Related Work
In addition to the time lock puzzle of [43] mentioned above, an alternative construction is by Bitansky et al. [8] assuming a strong form of randomized encodings and the existence of inherently sequential functions. While the time-lock puzzle of [43] is only privately verifiable, Boneh and Naor [12] showed a method to prove that the time-lock puzzle has a solution. Jerschow and Mauve [29] and Lenstra and Wesolowski [33] constructed iteratively sequential functions based on Dwork and Naor’s slow function [22] (which is based on hardness of modular exponentiations).
PPAD Hardness. The complexity class \(\mathsf {PPAD}\) (standing for Polynomial Parity Arguments on Directed graphs), introduced by Papadimitriou [39], is one of the central classes in \(\mathsf {TFNP}\). It contains the problems that can be shown to be total by a parity argument. This class is famous most notably since the problem of finding a Nash equilibrium in bimatrix games is complete for it [14, 19]. The class is formally defined by one of its complete problems End-Of-Line (EOL).
Bitansky, Paneth, and Rosen [9] introduced the Sink-of-Verifiable-Line (SVL) problem and showed that it reduces to the EOL problem (based on Abbot et al. [5] who adapted the reversible computation idea of Bennet [7]). They additionally gave an SVL instance which is hard assuming sub-exponentially secure indistinguishability obfuscation and one-way functions. These underlying assumptions were somewhat relaxed over the years yet remain in the class of obfuscation-type assumptions which are still considered very strong [25, 31, 32].
Hubáček and Yogev [28] observed that the Sink-of-Verifiable-Line actually reduces to a more structured problem, which they termed End-Of-Metered-Line (EOML), which in turn resides in \(\mathsf {CLS}\) (standing for Continuous Local Search), a subclass of \(\mathsf {PPAD}\). As a corollary, all of the above hardness results for \(\mathsf {PPAD}\) actually hold for \(\mathsf {CLS}\).
In an exciting recent work, Choudhuri et al. [15] introduced a relaxation of SVL, termed relaxed-SVL (rSVL) which still reduces to EOML and therefore can be used to prove hardness of \(\mathsf {PPAD}\) and \(\mathsf {CLS}\). They were able to give a hard rSVL instance based on the sum-check protocol of [35] assuming soundness of the Fiat-Shamir transformation and that #SAT is hard.
Verifiable Delay Functions. VDFs were recently introduced and constructed by Boneh, Bonneau, Bünz, and Fisch [10]. Following that work, additional constructions were given in [23, 40, 45]. The constructions of Pietrzak [40] and Wesolowski [45] are based on the repeated squaring assumption plus the Fiat-Shamir heuristic, while the construction of De Feo et al. [23] relies on elliptic curves and bilinear pairings. We refer to Boneh et al. [11] for a survey.
VDFs have numerous applications to the design of reliable distributed systems; see [10, Section 2]. Indeed, they are nowadays widely used in the design of reliable and resource efficient blockchains (e.g., in the consensus mechanism of the Chia blockchain [1]) and there is a collaboration [4] between the Ethereum Foundation [2], Protocol Labs [3], and various academic institutions to design better and more efficient VDFs.
Proofs of Sequential Work. Proofs of sequential work, suggested by Mahmoody, Moran, and Vadhan [36], are proof systems where on input a random challenge and time parameter t one can generate a publicly verifiable proof making t sequential computations, yet it is computationally infeasible to find a valid proof in significantly less than t sequential steps. Mahmoody et al. [36] gave the first construction and Cohen and Pietrzak [18] gave a simple and practical construction (both in the random oracle model). A recent work of Döttling et al. [21] constructs an incremental PoSW based on [18]. The techniques underlying Döttling et al’s construction are related in spirit to ours though the details are very different. See Sect. 2 for a comparison. All of the above constructions of PoSWs do not satisfy uniqueness, which is a major downside for many applications (see [10] for several examples). Indeed, VDFs were introduced exactly to mitigate this issue. Since our construction satisfies (computational) uniqueness, we actually get the first unique incremental PoSW.
Concurrent Works. In a concurrent and independent work, Choudhuri et al. [16] show \(\mathsf {PPAD}\)-hardness based on the Fiat-Shamir heuristic and the repeated squaring assumption. Their underlying techniques are related to ours since they use a similar tree-based proof merging technique on top of Pietrzak’s protocol [40]. However, since they use a ternary tree (while we use a high arity tree) their construction cannot be used to get a continuous VDF (and its applications). Also, for \(\mathsf {PPAD}\)-hardness, their construction requires Fiat-Shamir for protocols with \(\omega (\log \lambda )\) rounds (where \(\lambda \) is the security parameter) while we need Fiat-Shamir for \(\omega (1)\)-round protocols.
VDFs were also studied in two recent independent works by Döttling et al. [20] and Mahmoody et al. [37]. Both works show negative results for black-box constructions of VDFs in certain regimes of parameters in the random oracle model. The work of Döttling et al. [20] additionally shows that certain VDFs with a somewhat inefficient evaluator can be generically transformed into VDFs where the evaluator has optimal sequential running time. Whether such a transformation exists for cVDFs is left for future work.
2 Technical Overview
We start by informally defining a cVDF. At a high level, a cVDF specifies an iteratively sequential function \(\mathsf {Eval}\) where each iteration of the function gives a step of computation. Let \(x_0\) be any starting point and \(x_t = \mathsf {Eval}^{(t)}(x_{0})\) be the tth step or state given by the cVDF. We let \(B\) be an upper bound on the total number of steps in the computation, and assume that honest parties have some bounded parallelism \(\mathrm {polylog} (B)\) while adversarial parties may have parallelism \(\mathrm {poly} (B)\). For each step \(t \le B\), we require the following properties to hold:
-
Completeness: \(x_t\) can be verified as the tth state in time \(\mathrm {polylog} (t)\).
-
Adaptive Soundness: Any value \(x_t' \not = x_t\) computed by an adversarial party will not verify as the tth state (even when the starting point \(x_0\) is chosen adaptively). That is, each state is (computationally) unique.
-
Iteratively Sequential: Given an honestly sampled \(x_0\), adversarial parties cannot compute \(x_t\) in time \((1-\epsilon ) \cdot t \cdot \ell \), where \(\ell \) is the time for an honest party to compute a step of the computation.
We require adaptive soundness due to the distributed nature of a cVDF. In particular, suppose a new party starts computing the cVDF after t steps have elapsed. Then, \(x_{t}\) is the effective starting point for that party, and they may compute for \(t'\) more steps to obtain a state \(x_{t+t'}\). We want to ensure that soundness holds for the computation from \(x_{t}\) to \(x_{t+t'}\), so that the next party that starts at \(x_{t+t'}\) can trust the validity of \(x_{t+t'}\). Note that the above definition does not contain any proofs, but instead the states are verifiable by themselves. In terms of plain VDFs, this verifiability condition is equivalent to the case where the VDF is unique, meaning that the proofs are empty or included implicitly in the output.
To construct a cVDF, we start with a plain VDF. For simplicity in this overview, we assume that this underlying VDF is unique.
A First Attempt. The naïve approach for using a VDF to construct a cVDF is to iterate the VDF as a chain of computations. For any “base difficulty” T, which will be the time to compute a single step, we can use a VDF to do the computation from \(x_0\) to \(x_{T}\) with an associated proof of correctness \(\pi _{0 \rightarrow T}\). Then, we can start a new VDF instance starting at \(x_{T}\) and compute until \(x_{2T}\) with a proof of correctness \(\pi _{T \rightarrow 2T}\). At this point, anyone can verify that \(x_{2T}\) is correct by verifying both \(\pi _{0\rightarrow T}\) and \(\pi _{T \rightarrow 2T}\). We can continue this process indefinitely.
This solution has the property that after t steps, another party can pick up the current value \(x_{t \cdot T}\), verify it by checking each of the proofs computed so far, and then continue the VDF chain. In other words, there is no unverified internal state after t steps of the computation. Still, this naïve solution has the following major drawback (violating completeness). The final proof \(\pi _{(t-1)\cdot T \rightarrow t\cdot T}\) only certifies that computing a step from \(x_{(t-1)\cdot T}\) results in \(x_{t\cdot T}\) and does not guarantee anything about the computation from \(x_{0}\) to \(x_{(t-1)\cdot T}\). As such, we need to retain and check all proofs \(\pi _{0 \rightarrow T}, \ldots , \pi _{(t-1)\cdot T \rightarrow t\cdot T}\) computed so far to be able to verify \(x_{t\cdot T}\). Therefore, both the proof size and verification time scale linearly with t. We note that this idea is not new (e.g., see [10]), but nevertheless it does not solve our problem. Wesolowski [45] partially addresses this issue by showing how to aggregate proofs so the proof size does not grow, but the verification time in his protocol still grows.
One possible idea to overcome the blowup mentioned above is to use generic proof merging techniques. These can combine two different proofs into one that certifies both but whose size and verification time are proportional to that of a single one. Such techniques were given by Valiant [44] and Chung et al. [17]. However, being generic, they rely on strong assumptions and do not give the properties that we need (for example, efficiency and uniqueness). We next look at a promising—yet failed—attempt to overcome this.
A Logarithmic Approach. Since we can implement the above iterated strategy for any fixed interval T, we can simply run \(\log B\) many independent iterated VDF chains in parallel at the intervals \(T = 1, 2, 4, \ldots , 2^{\log B}\). Now say that we want to prove that \(x_{11}\) is the correct value eleven steps from the starting point \(x_0\). We just need to verify the proofs \(\pi _{0 \rightarrow 8}\), \(\pi _{8 \rightarrow 10}\), and \(\pi _{10 \rightarrow 11}\). For any number of steps t, we can now verify \(x_{t}\) by verifying only \(\log (t)\) many proofs, so we have resolved the major drawbacks! Furthermore, the prover can maintain a small state at each step of the computation by “forgetting” the smaller proofs. For example, after completing a proof \(\pi _{0 \rightarrow 2T}\) of size 2T, the prover no longer needs to store the proofs \(\pi _{0 \rightarrow T}\) and \(\pi _{T \rightarrow 2T}\).
Unfortunately, we have given up the distributed nature of a continuous VDF. Specifically, completeness fails to hold. Each “step” of the computation that the prover does to compute \(x_t\) with its associated proofs is no longer an independent instance of a single VDF computation. Rather, upon computing \(x_{t}\), the current prover has some internal state for all of the computations which have not yet completed at step t. Since a VDF only provides a way to prove that the output of each VDF instance is correct, then a new party who wants to pick up the computation has no way to verify the internal states of the unfinished VDF computations. As a result, this solution only works in the case where there is one trusted party maintaining the state of all the current VDF chains over a long period of time. In contrast, a cVDF ensures that there is no internal state at each step of the computation (or equivalently that the internal state is unique and can be verified as part of the output).
At an extremely high level, our continuous VDF builds off of this failed attempt when applied to the protocol of Pietrzak [40]. We make use of the algebraic structure of the underlying repeated squaring computation to ensure that the internal state of the prover is verifiable at every step and can be efficiently continued.
2.1 Adapting Pietrzak’s VDF
We next give a brief overview of Pietrzak’s sumcheck-style interactive protocol for repeated squaring and the resulting VDF. Let \(N=p\cdot q\) where p and q are safe primes and consider the language
that corresponds to valid repeated squaring instances with at most B exponentiations (where we think of B as smaller than the time to factor N). In order for the prover to prove that \((x,y,t) \in \mathcal {L} _{N,B}\) (corresponding to t steps of the computation), it first computes \(u=x^{2^{t/2}}\). It is clearly enough to then prove that \(u=x^{2^{t/2}}\) and that \(u^{2^{t/2}}=y\). However, recursively proving both statements separately is too expensive. The main observation of Pietrzak is that using a random challenge r from the verifier, one can merge both statements into a single one \(u^r y = (x^r u)^{2^{t/2}}\) which is true if and only if the original two statements are true (with high probability over r). We emphasize that proving that \(u^r y = (x^r u)^{2^{t/2}}\) has the same form as our original statement, but with difficulty t/2. This protocol readily gives a VDF by applying the Fiat-Shamir heuristic [24] on the \(\log _2 B\) round interactive proof.
From the above, it is clear that the only internal state that the prover needs to maintain in Pietrzak’s VDF consists of the midpoint \(u = x^{2^{t/2}}\) and the output \(y = x^{2^{t}}\). Thus, if we want another party to be able to pick up the computation at any time, we need to simultaneously prove the correctness of u in addition to y. Note that proving the correctness of u just requires another independent VDF instance of difficulty t/2. This results in a natural recursive tree-based structure where each computation of t steps consists of proving three instances of size t/2: \(u = x^{2^{t/2}}\), \(y = u^{2^{t/2}}\), and \(u^r y = (x^r u)^{2^{t/2}}\). Consequently, once these three instances are proven, it directly gives a proof for the “parent” instance \(x^{2^{t}} = y\). Note that this parent proof only need to consist of u, y, and a proof that \(u^r y = (x^r u)^{2^{t/2}}\) (in particular, it does not require proofs of the first two sub-computations, since they are certified by the proof of the third).
This suggests a high-level framework for making the construction continuous: starting at the root where we want to compute \(x^{2^{t}}\), recursively compute and prove each of the three sub-instances. Specifically, each step of the cVDF will be a step in the traversal of this tree. At any point when all three sub-instances of a node have been proven, merge the proofs into a proof of the parent node and “forget” the proofs of the sub-instances. This has the two desirable properties we want for a cVDF—first, at any point a new party can verify the state before continuing the computation, since the state only contains the nodes that have been completed; second, due to the structure of the proofs, the proof size at any node is bounded roughly by the height of the tree and hence avoids a blowup in verification time.
Proof Merging. The above approach heavily relies on the proof merging technique discussed above, namely that proofs of sub-instances of a parent node can be efficiently merged into a proof at that parent node. We obtain this due to the structure of the proofs in Pietrzak’s protocol. We note that similar proof merging techniques for specific settings were recently given by Döttling et al. [21] (in the context of incremental PoSW) and Choudhuri et al. [15] (in the context of constructing a hard rSVL instance). While their constructions are conceptually similar to ours, our construction for a cVDF introduces many challenges in order to achieve both uniquely verifiable states and a tight gap between honest and malicious evaluation. Döttling et al. [21] build on the Cohen and Pietrzak [18] PoSW and use a tree-based construction to make it incremental. At a high level, [18] is a PoSW based on a variant of Merkle trees, where the public verification procedure consists of a challenge for opening a random path in the tree and checking consistency. The main idea of Döttling et al. is to traverse the tree in a certain way and remember a small intermediate state which enables them to continue the computation incrementally. Moreover, they provide a proof at each step by creating a random challenge which “merges” previously computed challenges. The resulting construction is only a PoSW (where neither the output nor the proof are unique) and therefore does not suffice for our purpose. Choudhuri et al. [15] show how to merge proofs in the context of the #SAT sum-check protocol. There, they modify the #SAT proof system to be incremental by performing many additional recursive sub-computations, which is sufficient for their setting but in ours would cause a large gap between honest and malicious evaluation. We note that our method of combining proofs by proving a related statement is reminiscent of the approach of [15].
Before discussing the technical details of our tree-based construction, we first go over modifications we make to Pietrzak’s interactive protocol. Specifically, we discuss adaptive soundness, and we show how to achieve tight sequentiality (meaning that for any T, computing the VDF with difficulty T cannot be done significantly faster than T) in order to use it for our cVDF.
Achieving Adaptive Soundness. In order to show soundness, we requires the verifier to be able to efficiently check that the starting point of any computation is a valid generator of \(\mathsf {QR}_{N} \). To achieve this, we use the fact that there is an efficient way to test if x generates \(\mathsf {QR}_{N} \) given the square root of x (see Fact 3.6). As a result, we work with the square roots of elements in our protocol, which slightly changes the language. Namely, x, y are now square roots and \((x,y,t)\in \mathcal {L} _{N,B}\) if \((x^{2})^{2^{t}}=y^2 \mathrm {\text { }mod}\text { } N\).Footnote 8 We note that, following [40], working in \(\mathsf {QR}_{N} ^{+}\), the group of signed quadratic residues, would also give adaptive soundness (without including the square roots). This holds as soundness of Pietrzak’s protocol can be based on the low order assumption, and \(\mathsf {QR}_{N} ^{+}\) has no low order elements [11].Footnote 9
Bounding the Fraction of Intermediate Proofs. Recall that to compute \(y = x^{2^{t}}\) using the VDF of Pietrzak for our proposed cVDF, the honest party recursively proves three different computations of t/2 squarings, so that each step will be verifiable. This results in computing for at least time \(t^{\log _2 3}\), since it corresponds to computing the leaves of a ternary tree of depth \(\log _{2}(t)\), and each leaf requires a squaring. Note that this does not even consider the overhead of computing each proof, only the squarings. However, an adversary (even without parallelism) can shortcut this method and compute the underlying VDF to prove that \(y = x^{2^{t}}\) by computing roughly t squarings (and then computing the proof, which has relatively low overhead).
We deal with this issue by reducing the fraction of generating the intermediate proofs in Pietrzak’s protocol. Our solution is to (somewhat paradoxically) modify Pietrzak’s protocol to keep additional state, which we will need to verify. Specifically, we observe that t squarings can be split into k different segments. To prove that \(y=x^{2^t}\), the prover splits the computation into k segments each with difficulty t/k:
Using a random challenge \((r_{1},\ldots ,r_{k})\) from the verifier, we are able to combine these k segments into a single statement \((\prod _{i=1}^{k} (x_{i-1})^{r_{i}})^{t/k} = \prod _{i=1}^{k} (x_{i})^{r_{i}}\) (where \(x_{0} = x\)) which is true if and only if all of the segments are true (with high probability over the challenge). We call the combined statement the sketch.Footnote 10 Now in the recursive tree-based structure outlined above, a computation of t steps consists of proving \(k+1\) instances of size t/k. By choosing k to be proportional to the security parameter \(\lambda \), the total fraction of extra proofs in the honest computation of t steps is now sublinear in t. As an additional benefit when \(k = \lambda \), we note that the interactive protocol has \(\log _{\lambda }B \in O(1)\) rounds if B is a fixed polynomial in \(\lambda \) (as opposed to \(O(\log \lambda )\) rounds when \(k = 2\) corresponding to Pietrzak’s protocol). Applying the Fiat-Shamir heuristic to a constant-round protocol is a more standard assumption.Footnote 11
Bounding the Overhead of Each Step. Even though we have bounded the total fraction of extra nodes that the honest party has to compute, this does not suffice to achieve the tight gap between honest and adversarial computation for our proposed cVDF. Specifically, the honest computation has an additive (fixed) polynomial overhead \(\lambda ^{d}\)—for example, to check validity of the inputs and sometimes compute the sketch node—an adversary does not have to do so at each step. To compensate for this, we make each base step of the cVDF larger: namely, we truncate the tree. The effect of this is that a single step now takes time \(\lambda ^{d'}\) for \(d' > d\).
2.2 Constructing a Continuous VDF
As outlined above, our main insight is designing a cVDF based on a tree structure where each intermediate state of the computation can be verified and proofs of the computation can be efficiently merged. More concretely, the steps of computation correspond to a specific traversal of a \((k+1)\)-ary tree of height \(h = \log _{k} B\). Each node in the tree is associated to a statement \((x,y,t,\pi )\) for the underlying VDF, where \(y = x^{2^{t}}\) and \(\pi \) is the corresponding proof of correctness. We call x the node’s input, y its output, \(\pi \) the proof, and t the difficulty. The difficulty is determined by its height in the tree, namely, a node at distance l from the root has difficulty \(t=k^{h-l}\) (so nodes closer to the leaves take less time to compute).
In more detail, the tree is defined as follows. Starting at the root with input \(x_{0}\) and difficulty \(t = k^{h}\), we divide it into k segments \(x_{1},\ldots ,x_{k}\), analogous to our VDF construction. These form the inputs and outputs of its first k children: its ith child will have input \(x_{i-1}\) and output \(x_{i}\), and requires a proof that \((x_{i-1})^{t/k} = x_{i}\). Its \((k+1)\)-st child corresponds to the sketch, namely a node where the k statements of the siblings are merged into a single statement. Recursively splitting statements this way gives the statement at each node in the tree, until reaching the leaves where squaring can be done directly. Note that with this structure, only the leaves require computation—the statement of nodes at greater heights can be deduced from the statements of their children (which gives us a way to efficiently merge proofs “up” the tree as we described above).
As a result, we would like each step of computation in the cVDF to correspond to computing the statement of a single leaf. Accomplishing this requires being able to compute the input x of the leaf from the previous state (from which y can be computed via squaring). By the structure of our tree, we observe that this only requires knowing a (small) subset of nodes that were already computed, which we call the frontier. The frontier of a leaf s, denoted \(\mathsf {frontier} (s)\), contains all the left siblings of its ancestors, including the left siblings of s itself.Footnote 12 Therefore, a state in the computation contains a leaf label s and the statements associated with the nodes in \(\mathsf {frontier} (s)\), which contains at most \(k\cdot \log _{k} (B)\) nodes. A single step of our continuous VDF, given a state \(v=(s,\mathsf {frontier} (s))\), first verifies v and then computes the next state \(v'=(s',\mathsf {frontier} (s'))\) where \(s'\) is the next leaf after s. See Fig. 1 for an illustration of computing the next state.
This is the basic template for our continuous VDF. Next, we discuss some of the challenges that come up related to efficiency and security.
Ensuring the Iteratively Sequential Property. Recall that we want to obtain a tight gap between honest and malicious evaluation of the continuous VDF for any number of steps. A priori, it seems that computing a sketch for each node in the tree adds a significant amount of complexity to the honest evaluation. To illustrate this, suppose a malicious evaluator wants to compute the statement \((x,y,t,\pi )\) at the root. This can be done by skipping the sketch nodes for intermediate states and only computing a proof for the final output \(y = x^{2^{t}}\), which in total involves t squarings (corresponding to computing the leaves of a k-ary tree of height \(\log _{k}t\)) along with the sketch node for the root. However, for an honest evaluator, this requires computing \((k+1)^{\log _{k}t}\) leaf nodes (corresponding to every leaf in a \((k+1)\)-ary tree of height \(\log _{k}t\)). Therefore, the ratio is \(\alpha = ((k+1)/k)^{\log _{k}t}\). In order to get the tight gap, we choose k to be proportional to the security parameter so that \(\alpha = (1+o(1)) \cdot t\). This change is crucial (as we eluded towards above), as otherwise if k is a constant, the relative overhead would be significant. Indeed, in Pietrzak’s protocol, \(k = 2\) and computing the sketch node constitutes a constant fraction of the computation.
2.3 The Efficiency of Our Construction
In this section, we briefly compare the efficiency of our constructions to previous ones which are based on repeated squaring. Specifically, we discuss Wesolowki’s VDF [45] (denoted WVDF), Pietrzak’s VDF [40] (denoted PVDF), in comparison to our cVDF using a tree of arity k (denoted k-cVDF) and the VDF underlying it (denoted k-VDF), which is simply Pietrzak’s VDF with arity k.
For proof length corresponding to t squares, the WVDF proof is just a single group element, and the PVDF proof consists of \(\log _{2}(t)\) group elements. For the k-VDF, generalizing Pietrzak’s VDF to use a tree with arity k results in a proof with \((k-1) \cdot \log _{k}(t)\) group elements. Finally, the k-cVDF output consists of a frontier with at most \((k-1)\) proofs for a k-VDF in each of \(\log _{k}(t)\) levels of the tree, resulting in \((k-1)^{2}(\log _{k}(t))^{2}\) group elements. In all cases, verifying a proof with n group elements requires doing \(O(n \cdot \lambda )\) squares. For prover efficiency, the honest prover can compute the proof in the time to do \(t(1+o(t))\) squares (when \(t \in \mathrm {poly} (\lambda )\) and \(k \in \varOmega (\log \lambda )\) for the k-cVDF).
In the full cVDF construction, we set k to be equal to \(\lambda \) for simplicity, but as the above shows, different values of k give rise to different efficiency trade-offs.
3 Preliminaries
In this section, we give relevant definitions and notation. Additional preliminaries, including definitions of interactive protocols and the Fiat-Shamir heuristic, are deferred to the full version.
3.1 Verifiable, Sequential, and Iteratively Sequential Functions
In this section, we define different properties of functions which will be useful in subsequent sections when we define unique VDFs (Definition 5.1) and continuous VDFs (Definition 6.1). All of our definitions will be in the public parameter model. We start by defining a verifiable function.
Definition 3.1
(Verifiable Functions). Let \(B:\mathbb {N} \rightarrow \mathbb {N} \). A \(B\)-sound verifiable function is a tuple of algorithms \((\mathsf {Gen}, \mathsf {Eval}, \mathsf {Verify})\) where \(\mathsf {Gen} \) is PPT, \(\mathsf {Eval}\) is deterministic, and \(\mathsf {Verify} \) is deterministic polynomial-time, satisfying the following property:
-
Perfect Completeness. For every \(\lambda \in \mathbb {N} \), \(\mathsf {pp} \in \mathrm {Supp}\left( \mathsf {Gen} (1^\lambda )\right) \), and \(x \in \{0,1\}^{*}\), it holds that
$$\mathsf {Verify} (1^\lambda , \mathsf {pp},x,\mathsf {Eval}(1^\lambda ,\mathsf {pp},x)) = 1.$$ -
\(\varvec{B}\)-Soundness. For every non-uniform algorithm \(\mathcal {A} = \left\{ \mathcal {A} _{\lambda }\right\} _{\lambda \in \mathbb {N}}\) such that \(\mathsf {size} (A_{\lambda }) \in \mathrm {poly} (B(\lambda ))\) for all \(\lambda \in \mathbb {N} \), there exists a negligible function \(\mathsf {negl} \) such that for every \(\lambda \in \mathbb {N} \) it holds that
$$\begin{aligned} \mathrm {Pr}\left[ \begin{array}{l} \mathsf {pp} \leftarrow \mathsf {Gen} (1^\lambda ) \\ (x,y) \leftarrow \mathcal {A} _{\lambda }(\mathsf {pp}) \\ \end{array} : \mathsf {Verify} (1^\lambda , \mathsf {pp},x,y) = 1 \wedge \mathsf {Eval}(1^\lambda , \mathsf {pp},x) \ne y \right] \le \mathsf {negl} (\lambda ). \end{aligned}$$
Next, we define a sequential function. At a high level, this is a function f implemented by an algorithm \(\mathsf {Eval}\) that takes input (x, t), such that computing f(x, t) requires time roughly t, even with parallelism. Our formal definition is inspired by [10]. Intuitively, it requires that any algorithm \(\mathcal {A} _{0,\lambda }\) which first pre-processes the public parameters cannot output a circuit \(\mathcal {A} _{1}\) satisfying the following. Upon receipt of a freshly sampled input x, \(\mathcal {A} _{1}\) outputs a value y and a difficulty t, where y is the output of \(\mathsf {Eval}\) on x for difficulty t, where t is sufficiently larger than its depth. This captures the notion that \(\mathcal {A} _{1}\) manages to compute y in less than t time, even with large width.
The first six states of our continuous VDF with \(k=3\) and base difficulty \(D = k^{d'}\) for a constant \(d'\). In each tree, the segment nodes are given by solid lines and the sketch nodes by dashed lines. The yellow node is the current leaf, and the pink nodes are its frontier. The values in blue are contain \((x,y,\pi )\) for the corresponding node. The proofs \(\pi \) at leaf nodes with input x and output y correspond to the underlying VDF proof that \(x^{2^{D}} = y\), and the proofs at each higher node consist of its segments (outputs of k first children) and of the proof of the sketch node (the \((k+1)\)st child). (Color figure online)
Definition 3.2
Let \(D,B,\ell :\mathbb {N} \rightarrow \mathbb {N} \) and let \(\epsilon \in (0,1)\). A \((D, B,\ell ,\epsilon )\)-sequential function is a tuple \((\mathsf {Gen}, \mathsf {Sample}, \mathsf {Eval})\) where \(\mathsf {Gen} \) and \(\mathsf {Sample} \) are PPT, \(\mathsf {Eval}\) is deterministic, and the following properties hold:
-
Honest Evaluation. There exists a uniform circuit family \(\left\{ C_{\lambda ,t}\right\} _{\lambda ,t\in \mathbb {N}}\) such that \(C_{\lambda ,t}\) computes \(\mathsf {Eval}(1^\lambda ,\cdot ,(\cdot ,t))\), and for all sufficiently large \(\lambda \in \mathbb {N} \) and \(D(\lambda ) \le t \le B(\lambda )\), it holds that \(\mathsf {depth}{} (C_{\lambda ,t}) = t \cdot \ell (\lambda )\) and \(\mathsf {width} (C_{\lambda ,t}) \in \mathrm {poly} (\lambda )\).
-
Sequentiality. For all non-uniform algorithms \(\mathcal {A} _{0} = \left\{ \mathcal {A} _{0,\lambda }\right\} _{\lambda \in \mathbb {N}}\) such that \(\mathsf {size} (\mathcal {A} _{0,\lambda }) \in \mathrm {poly} (B(\lambda ))\) for all \(\lambda \in \mathbb {N} \), there exists a negligible function \(\mathsf {negl} \) such that for every \(\lambda \in \mathbb {N} \),
$$\begin{aligned} \mathrm {Pr}\left[ \begin{array}{l} \mathsf {pp} \leftarrow \mathsf {Gen} (1^\lambda ) \\ \mathcal {A} _{1} \leftarrow \mathcal {A} _{0,\lambda }(\mathsf {pp}) \\ x \leftarrow \mathsf {Sample} (1^\lambda ,\mathsf {pp}) \\ (t,y) \leftarrow \mathcal {A} _{1}(x) \\ \end{array} : \begin{array}{l} \mathsf {Eval}(1^\lambda , \mathsf {pp},(x,t)) = y \\ \wedge \ \mathsf {depth}{} (\mathcal {A} _{1}) \le (1-\epsilon ) \cdot t \cdot \ell (\lambda ) \\ \wedge \ t \ge D(\lambda ) \end{array} \right] \le \mathsf {negl} (\lambda ). \end{aligned}$$
Next, we define an iteratively sequential function. This is a function f implemented by an algorithm \(\mathsf {Eval}\), such that the t-wise composition of f cannot be computed faster than computing f sequentially t times, even using parallelism. We also require that the length of the output of f is bounded, so that it does not grow with the number of compositions.
Definition 3.3
(Iteratively Sequential Function). Let \(D,B,\ell :\mathbb {N} \rightarrow \mathbb {N} \) be functions and let \(\epsilon \in (0,1)\). A tuple of algorithms \((\mathsf {Gen},\mathsf {Sample},\mathsf {Eval})\) is a \((D, B, \ell ,\epsilon )\)-iteratively sequential function if \(\mathsf {Gen} \) and \(\mathsf {Sample} \) are PPT, \(\mathsf {Eval}\) is deterministic, and the following properties hold.
-
Length Bounded. There exists a polynomial \(m\) such that for every \(\lambda \in \mathbb {N} \) and \(x \in \{0,1\}^{*}\), it holds that \(\left| \mathsf {Eval}(1^\lambda ,\mathsf {pp},x) \right| \le m(\lambda )\). We define \(\mathsf {Eval}^{(\cdot )}\) to be the function that takes as input \(1^\lambda ,\mathsf {pp} \), and (x, T) and represents the T-wise composition given by
$$\begin{aligned} \mathsf {Eval}^{(T)}(1^\lambda ,\mathsf {pp},x) {\mathop {=}\limits ^{\mathsf {def}}} \underbrace{\mathsf {Eval}(1^\lambda ,\mathsf {pp},\cdot ) \circ \ldots \circ \mathsf {Eval}(1^\lambda ,\mathsf {pp},\cdot )}_{T \text { times}}(x) \end{aligned}$$and note that this function is also length bounded.
-
Iteratively sequential. The tuple \((\mathsf {Gen},\mathsf {Sample},\mathsf {Eval}^{(\cdot )})\) is a \((D, B,\ell ,\epsilon )\)-sequential function.
Remark 3.4
(Decoupling size and depth). We note that one can also consider a generalization of a \((D,B,\ell ,\epsilon )\)-sequential function to a \((D,U,B,\ell ,\epsilon )\)-sequential function (and thus iteratively sequential functions), where the size of \(\mathcal {A} _{0,\lambda }\) remains bounded by \(\mathrm {poly} (B(\lambda ))\), but the parameter t output by \(\mathcal {A} _{1}\) must be at most \(U(\lambda )\).
3.2 Repeated Squaring Assumption
The repeated squaring assumption (henceforth, the RSW assumptionFootnote 13) roughly says that there is no parallel algorithm that can perform t squarings modulo an RSA integer N significantly faster than just performing t squarings sequentially. This implicitly assumes that N cannot be factored efficiently. This assumption has been very useful for various applications (e.g., time-lock puzzles [43], reliable benchmarking [13], and timed commitments [12, 34] and to date there is no known strategy that beats the naive sequential one.
Define \(\mathsf {RSW} = (\mathsf {RSW}.\mathsf {Gen}, \mathsf {RSW}.\mathsf {Sample}, \mathsf {RSW}.\mathsf {Eval})\) as follows.
-
\(N \leftarrow \mathsf {RSW}.\mathsf {Gen} (1^\lambda )\) :
Sample random primes \(p', q'\) from \([2^\lambda , 2^{\lambda + 1})\) such that \(p = 2p' + 1\) and \(q = 2q' + 1\) are prime, and output \(N = p\cdot q\).
-
\(x \leftarrow \mathsf {RSW}.\mathsf {Sample} (1^\lambda ,N)\) :
Sample and output a random element \(g \leftarrow \mathbb {Z} _{N}^{\star } \).
-
\(y \leftarrow \mathsf {RSW}.\mathsf {Eval}(1^\lambda , N, g)\) :
Output \(y = g^{2} \mathrm {\text { }mod}\text { } N\).
Assumption 3.5
(RSW Assumption). Let \(D,B:\mathbb {N} \rightarrow \mathbb {N} \). The \((D, B)\)-RSW assumption is that there exists a polynomial \(\ell \in \mathbb {N} \rightarrow \mathbb {N} \) and constant \(\epsilon \in (0,1)\) such that \(\mathsf {RSW} \) is a \((D, B,\ell , \epsilon )\)-iteratively sequential function.
Note that the RSW assumption implies that factoring is hard. Namely, no adversary can factor an integer \(N = p\cdot q\) where p and q are large “safe” primes (a prime p is safe if \(p-1\) has two factors, 2 and \(p'\), for some prime number \(p' \in [2^\lambda , 2^{\lambda + 1})\)).
3.3 Number Theory Facts
For \(N \in \mathbb {N} \) and any \(x \in \mathbb {Z} _N \), we use the notation  to denote \(\min \left\{ x,N-x\right\} \). Next, we state three standard useful facts. The proofs are deferred to the full version.
to denote \(\min \left\{ x,N-x\right\} \). Next, we state three standard useful facts. The proofs are deferred to the full version.
Fact 3.6
Let \(N \in \mathrm {Supp}\left( \mathsf {RSW}.\mathsf {Gen} (1^\lambda )\right) \). Then, for \(\mu \in \mathbb {Z} _{N}^{\star } \), it holds that \(\langle \mu \rangle = \mathsf {QR}_{N} \) if and only if there exists an \(x\in \mathbb {Z} _{N}^{\star } \) such that \(\mu = x^2\) and \(\gcd \,(x\pm 1,N) = 1\).
Fact 3.7
([41]). There exists a polynomial time algorithm \(\mathcal {A} \) such that for any \(\lambda \in \mathbb {N} \), N in the support of \(\mathsf {RSW}.\mathsf {Gen} (1^\lambda )\), and \(\mu ,x,x' \in \mathbb {Z} _N\), if \(\mu = x^2={x'}^2\) and \(x' \not \in \{x,-x\}\), then \(\mathcal {A} (1^\lambda , N, (\mu , x, x'))\) outputs (p, q) such that \(N = p \cdot q\).
Fact 3.8
Let \(N\in \mathrm {Supp}\left( \mathsf {RSW}.\mathsf {Gen} (1^\lambda )\right) \) and let \(\langle x \rangle =\mathsf {QR}_{N} \). Then, for any \(i \in \mathbb {N} \), it holds that \(\langle x^{2^{i}} \rangle = \mathsf {QR}_{N} \).
4 Interactive Proof for Repeated Squaring
In this section, we give an interactive proof for a language representing \(t \) repeated squarings. As discussed in Sect. 2, this protocol is based on that of [40]. We start with an overview. The common input includes an integer \(t \) and two values \(\widehat{x} _{0},\widehat{y} \in \mathbb {Z} _{N}^{\star } \), where, for the purpose of this overview, the goal is for the prover to convince the verifier that \(\widehat{y} = (\widehat{x} _{0})^{2^{t}} \mathrm {\text { }mod}\text { } N\). The protocol is defined recursively.
Starting with a statement \((\widehat{x} _{0},\widehat{y},t)\), where we assume for simplicity that \(t \) is a power of k, the prover splits \(x_{0}\) into k “segments”, where each segment is \(t/k\) “steps” of the computation of \((\widehat{x} _{0})^{2^{t}} \mathrm {\text { }mod}\text { } N\). The ith segment is recursively defined as the value \((\widehat{x} _{i-1})^{2^{t/k}}\). In other words, \(\widehat{x} _i = (\widehat{x} _0)^{2^{i\cdot t/k}}\) for all \(i \in \left\{ 0,1,\ldots ,k\right\} \). If one can verify the values of \(\widehat{x} _1,\ldots ,\widehat{x} _k\), then one can also readily verify that \(\widehat{y} = (\widehat{x} _{0})^{2^{t}} \mathrm {\text { }mod}\text { } N\). To verify the values of \(\widehat{x} _1,\ldots ,\widehat{x} _k\) efficiently we rely on interaction and require the prover to convince the verifier that the values \(\widehat{x} _1,\ldots ,\widehat{x} _k\) are consistent (in some sense) under a random linear relation. To this end, the prover and verifier engage in a second protocol to prove a modified statement \((\widehat{x} _{0}',\widehat{y} ', t/k)\) which combines all the segments and should only be true if all segments are true (with high probability). The modified statement is proved in the same way, where the exponent \(t/k\) is divided by k with each new statement. This process is continued \(\log _k t \) times until the statement to verify can be done by direct computation.
For soundness of our protocol, we need to bound the probability of a cheating prover jumping from a false statement in the beginning of the protocol to a true statement in one of the subsequent protocols. One technical point is that to accomplish this, we work in the subgroup \(\mathsf {QR}_{N}\) of \(\mathbb {Z} _{N}^{\star }\) and thus we want the starting point \(\widehat{x} _{0}\) to generate \(\mathsf {QR}_{N}\). To accommodate this, we let the prover provide a square root of every group element as a witness to the fact that it is in \(\mathsf {QR}_{N}\) (actually, by Fact 3.8, this will imply that all group elements generate \(\mathsf {QR}_{N}\)). Therefore, rather than working with \(\widehat{x} _{0}\) and \(\widehat{y} \) directly, we work with their square roots \(x_{0}\) and y, respectively. Hence, the common input consists of an integer \(t \) and \((x_{0},y)\), where the goal is actually to prove that \(y^{2} = (x_{0}^{2})^{2^{t}} = x_{0}^{2^{t +1}} \mathrm {\text { }mod}\text { } N\).
Note that, in general, the square root \(x_{0}\) is not unique in \(\mathbb {Z} _{N}^{\star }\) for a given square \(x_{0}^{2}\). Indeed, there are 4 square roots \(\pm x_{0}, \pm x_{0}'\). In our protocol, the computationally bounded prover can compute only two of them, either \(\pm x_{0}\) or \(\pm x_{0}'\), as otherwise, by Fact 3.7 we could use the prover to factor N. Among the two square roots that the prover can compute, we canonically decide that the prover must use the smaller one. This gives rise to our definition of a valid element x: \(x^{2} \mathrm {\text { }mod}\text { } N\) generates \(\mathsf {QR}_{N}\) and  , formally defined in Definition 4.1.
, formally defined in Definition 4.1.
4.1 Protocol
Before presenting the protocol, we first define the language. Toward that goal, we start with the formal definition of a valid element.
Definition 4.1
(Valid element). For any \(N\in \mathbb {N} \) and \(x\in \{0,1\}^{*}\), we say that x is a valid element if \(x \in \mathbb {Z} _{N}^{\star } \), \(\langle x^{2} \rangle = \mathsf {QR}_{N} \), and  . We say that a sequence of elements \(\left( x_{1},\ldots ,x_{\ell }\right) \) is a valid sequence if each element \(x_i\) is a valid element.
. We say that a sequence of elements \(\left( x_{1},\ldots ,x_{\ell }\right) \) is a valid sequence if each element \(x_i\) is a valid element.
By Fact 3.6, whenever N is in the support of \(\mathsf {RSW}.\mathsf {Gen} (1^\lambda )\), validity can be tested in polynomial time by verifying that  , and that \(\gcd (x \pm 1, N) = 1\) (and outputting 1 if and only if all checks pass). This algorithm naturally extends to one that receives as input a sequence of pairs and verifies each separately.
, and that \(\gcd (x \pm 1, N) = 1\) (and outputting 1 if and only if all checks pass). This algorithm naturally extends to one that receives as input a sequence of pairs and verifies each separately.
The language for our interactive proof, \(\mathcal {L} _{N,B} \), is parametrized by integers \(N\in \mathrm {Supp}\left( \mathsf {RSW}.\mathsf {Gen} (1^\lambda )\right) \) and \(B = B(\lambda )\), and it is defined as:
Intuitively, \(\mathcal {L} _{N,B} \) should be thought of as the language of elements \(x_{0},y\) where \(x_{0}\) is valid and \(x_{0}^{2^{t +1}} = y^{2} \mathrm {\text { }mod}\text { } N\). To be well-defined on any possible statement with \(x_{0},y \in \mathbb {Z} _{N}^{\star } \) and \(t\in \mathbb {N} \), we include statements with invalid elements \(x_{0}\) in the language. Since the verifier can test validity efficiently, this language still enforces that valid elements represent repeated squaring.
Our protocol \(\varPi _{\lambda ,k,d} \), given in Fig. 2, is parametrized by the security parameter \(\lambda \), as well as integers \(k=k(\lambda )\) and \(d=d(\lambda )\), where k is the number of segments into which we split each statement and d is a “cut-off” parameter that defines the base of the recursive protocol.
We show the following theorem, stating that \(\varPi _{\lambda ,k,d} \) is an interactive proof for the language \(\mathcal {L} _{N,B} \), by showing completeness and soundness. Furthermore, we prove an additional property which roughly shows that any cheating prover cannot deviate in a specific way from the honest prover strategy even for statements in the language. Due to lack of space, the proof is deferred to the full version.
Theorem 4.2
For any \(\lambda \in \mathbb {N} \), \(k=k(\lambda )\), \(d=d(\lambda )\), \(B=B(\lambda )\), and \(N \in \mathrm {Supp}\left( \mathsf {RSW}.\mathsf {Gen} (1^\lambda )\right) \), the protocol \(\varPi _{\lambda ,k,d} \) (given in Fig. 2) is a \((\log _k(B) -d) \cdot 3/2^{\lambda }\)-sound interactive proof for \(\mathcal {L} _{N,B} \).
5 Unique Verifiable Delay Function
In this section, we use the Fiat-Shamir heuristic to transform the interactive proof for the language \(\mathcal {L} _{N,B} \) corresponding to repeated squaring (given in Sect. 4) into a unique VDF.
Definition 5.1
(Unique Verifiable Delay Function). A \((D, B,\ell ,\epsilon )\)-unique verifiable delay function (uVDF) is a tuple \((\mathsf {Gen}, \mathsf {Sample}, \mathsf {Eval}, \mathsf {Verify})\) where \(\mathsf {Eval}\) outputs a value y and a proof \(\pi \), such that \((\mathsf {Gen}, \mathsf {Sample}, \mathsf {Eval})\) is a \((D, B, \ell , \epsilon )\)-sequential function and \((\mathsf {Gen}, \mathsf {Eval}, \mathsf {Verify})\) is a \(B\)-sound verifiable function.
5.1 Construction
For parameters k, d we define \((P_{\mathsf {FS}},V_{\mathsf {FS}})\) to be the result of applying the Fiat-Shamir transformation to the protocol \(\varPi _{\lambda ,k,d} \) for \(\mathcal {L} _{N,B} \) relative to some hash family \(\mathcal {H} \). At a high level, this construction computes repeated squares and then uses \(P_{\mathsf {FS}}\) and \(V_{\mathsf {FS}}\) to prove and verify that this is done correctly.
We start by defining helper algorithms in Fig. 3 based on the interactive protocol of Sect. 4. For notational convenience, we explicitly write algorithms \(\mathsf {FS} \hbox {-}\mathsf {Prove} \) and \(\mathsf {FS} \hbox {-}\mathsf {Verify} \), which take \(\mathsf {pp} = (N, B, k, d, \mathsf {hash}) \) as input, as well as \(((x_{0},t),y)\), where (N, B, k, d) correspond to the parameters of the non-interactive protocol and language, \(\mathsf {hash} \) is the hash function sampled from the hash family \(\mathcal {H} \) when applying the FS transform to \(\varPi _{\lambda ,k,d} \), and \(((x_{0},t),y)\) correspond to the statements of the language. We additionally define an efficient algorithm \(\mathsf {Sketch} \) that outputs the statement for the recursive step in the interactive proof \(\varPi _{\lambda ,k,d} \).
We emphasize that the algorithms in Fig. 3 are a restatement of the interactive protocol from Sect. 4 after applying the FS transform, given here only for ease of reading.
Next, we give a construction \(\mathsf {uVDF} \) of a unique VDF consisting of algorithms \((\mathsf {uVDF}.\mathsf {Gen}, \mathsf {uVDF}.\mathsf {Sample}, \mathsf {uVDF}.\mathsf {Eval}, \mathsf {uVDF}.\mathsf {Verify})\) relative to a function \(B :\mathbb {N} \rightarrow \mathbb {N} \).
-
\(\mathsf {pp} \leftarrow \mathsf {uVDF}.\mathsf {Gen} (1^\lambda )\) :
Sample \(N \leftarrow \mathsf {RSW}.\mathsf {Gen} (1^\lambda )\), \(\mathsf {hash} \leftarrow \mathcal {H} \), let \(k = \lambda \), \(B = B(\lambda )\), and let d be a constant which will be specified in the proof of sequentiality (in the full version), and output \(\mathsf {pp} = (N, B, k, d, \mathsf {hash}) \).
-
\(x_{0} \leftarrow \mathsf {uVDF}.\mathsf {Sample} (1^\lambda , \mathsf {pp})\) :
Sample and output a random element \(x_{0} \leftarrow \mathbb {Z} _{N}^{\star } \) such that \(\gcd (x_{0} \pm 1, N) = 1\) and
 .Footnote 14
.Footnote 14
-
\((y,\pi ) \leftarrow \mathsf {uVDF}.\mathsf {Eval}(1^\lambda , \mathsf {pp}, (x_0, t))\) :
If \(x_0\) is an invalid element, output \((\bot ,\bot )\). If \(t \le k^{d}\), compute
 and output \((y,\bot )\).
and output \((y,\bot )\).Otherwise, compute
 for \(i \in [k]\) and let \(\mathsf {msg} = (x_{1},\ldots ,x_{k-1})\) and \(y = x_{k}\). Let \((x'_{0},y') = \mathsf {Sketch} (\mathsf {pp},(x_{0},t),y,\mathsf {msg})\). Finally, output \((y,\pi )\) where \(\pi = (\mathsf {msg},\pi ')\) and \(\pi ' = \mathsf {FS} \hbox {-}\mathsf {Prove} (\mathsf {pp}, (x_0', t/k), y')\).
for \(i \in [k]\) and let \(\mathsf {msg} = (x_{1},\ldots ,x_{k-1})\) and \(y = x_{k}\). Let \((x'_{0},y') = \mathsf {Sketch} (\mathsf {pp},(x_{0},t),y,\mathsf {msg})\). Finally, output \((y,\pi )\) where \(\pi = (\mathsf {msg},\pi ')\) and \(\pi ' = \mathsf {FS} \hbox {-}\mathsf {Prove} (\mathsf {pp}, (x_0', t/k), y')\). -
\(b \leftarrow \mathsf {uVDF}.\mathsf {Verify} (1^\lambda , \mathsf {pp}, (x_0,t),(y, \pi ))\) :
If \(x_{0}\) is an invalid element or \(t > B\), output 1 if \(y = \pi = \bot \) and 0 if this is not the case. If y is invalid, then output 0. Otherwise, output \(\mathsf {FS} \hbox {-}\mathsf {Verify} (\mathsf {pp}, (x_0, t),y, \pi )\).
We prove the following theorem. Due to lack of space, the proof is deferred to the full version.
Theorem 5.2
Let \(D,B,\alpha :\mathbb {N} \rightarrow \mathbb {N} \) be functions satisfying \(D(\lambda ) \in \omega (\lambda ^{2})\), \(B(\lambda ) \in 2^{O(\lambda )}\), and \(\alpha (\lambda ) \le \lceil \log _\lambda (B(\lambda )) \rceil \). Suppose that the \(\alpha \)-round strong FS assumption holds and the \((D, B)\)-RSW assumption holds for polynomial \(\ell :\mathbb {N} \rightarrow \mathbb {N} \) and constant \(\epsilon \in (0,1)\). Then, for any constants \(\delta > 0\) and \(\epsilon ' > \frac{\epsilon +\delta }{1+\delta }\) it holds that \(\mathsf {uVDF}\) is a \((D, B, (1+\delta )\cdot \ell , \epsilon ')\)-unique verifiable delay function.
6 Continuous Verifiable Delay Function
In this section, we construct a cVDF. Intuitively, this is an iteratively sequential function where every intermediate state is verifiable. Throughout this section, we denote by \(\mathsf {Eval}^{(\cdot )}\) the composed function which takes as input \(1^\lambda \), \(\mathsf {pp} \), and (x, T), and runs the T-wise composition of \(\mathsf {Eval}(1^\lambda ,\mathsf {pp},\cdot )\) on input x.
We first give the formal definition of a cVDF. In the following definition, the completeness requirement says that if \(v_{0}\) is an honestly generated starting state, then the \(\mathsf {Verify} \) will accept the state given by \(\mathsf {Eval}^{(T)}(1^\lambda , \mathsf {pp}, v_{0})\) for any T. Note that when coupled with soundness, this implies that completeness holds with high probability for any intermediate state generated by a computationally bounded adversary.
Definition 6.1
(Continuous Verifiable Delay Function). Let \(B,\ell :\mathbb {N} \rightarrow \mathbb {N} \) and \(\epsilon \in (0,1)\). A \((B,\ell ,\epsilon )\)-continuous verifiable delay function (cVDF) is a tuple \((\mathsf {Gen}, \mathsf {Sample}, \mathsf {Eval}, \mathsf {Verify})\) such that \((\mathsf {Gen}, \mathsf {Sample}, \mathsf {Eval})\) is a \((1,B, \ell , \epsilon )\)-iteratively sequential function, \((\mathsf {Gen},\mathsf {Eval}^{(\cdot )},\mathsf {Verify})\) is a \(B\)-sound function, and it satisfies the following completeness property:
-
Completeness from Honest Start. For every \(\lambda \in \mathbb {N} \), \(\mathsf {pp} \) in the support of \(\mathsf {Gen} (1^\lambda )\), \(v_{0}\) in the support of \(\mathsf {Sample} (1^\lambda ,\mathsf {pp})\), and \(T\in \mathbb {N} \), it holds that \(\mathsf {Verify} (1^\lambda , \mathsf {pp},(v_{0},T),\mathsf {Eval}^{(T)}(1^\lambda ,\mathsf {pp},v_{0})) = 1\).
The main result of this section is stated next.
Theorem 6.2
(Continuous VDF). Let \(D,B,\alpha :\mathbb {N} \rightarrow \mathbb {N} \) be functions satisfying \(B(\lambda ) \le 2^{\lambda ^{1/3}}\), \(\alpha (\lambda ) = \lceil \log _\lambda (B(\lambda )) \rceil \), and \(D(\lambda ) \ge \lambda ^{d'}\) for all \(\lambda \in \mathbb {N} \) and for a specific constant \(d'\). Suppose that the \(\alpha \)-round strong FS assumption holds and the \((D, B)\)-RSW assumption holds for a polynomial \(\ell :\mathbb {N} \rightarrow \mathbb {N} \) and constant \(\epsilon \in (0,1)\). Then, for any constant \(\delta > 0\) and \(\epsilon ' > \frac{\epsilon +\delta }{1+\delta }\), it holds that \(\mathsf {cVDF} \) is a \((B, (1+\delta )\cdot D(\lambda ) \cdot \ell , \epsilon ')\)-cVDF.
In the case where we want to have a fixed polynomial bound on the number of iterations, we obtain the following corollary.
Corollary 6.3
(Restatement of Theorem 1.1). For any polynomials B, D where \(D(\lambda ) \ge \lambda ^{d'}\) for a specific constant \(d'\), suppose the O(1)-round strong FS assumption holds and the (D, B)-RSW assumption holds for a polynomial \(\ell :\mathbb {N} \rightarrow \mathbb {N} \) and constant \(\epsilon \in (0,1)\). Then, for any constant \(\delta > 0\) and \(\epsilon ' > \frac{\epsilon +\delta }{1+\delta }\), it holds that \(\mathsf {cVDF} \) is a \((B, (1+\delta )\cdot D(\lambda ) \cdot \ell , \epsilon ')\)-cVDF.
Remark 6.4
(Decoupling size and depth). The definition of a \((B,\ell ,\epsilon )\)-cVDF naturally extends to a \((U,B,\ell ,\epsilon )\)-cVDF, where we require \((\mathsf {Gen}, \mathsf {Sample},\mathsf {Eval})\) to be a \((1,U,B,\ell ,\epsilon )\)-iteratively sequential function; see Remark 3.4. Our construction will satisfy this for all functions U such that \(U(\lambda ) \le B(\lambda )\) for all \(\lambda \in \mathbb {N} \) Moreover, in this case, the above corollary can be based on the strong Fiat-Shamir assumption for \(\lceil \log _{\lambda }(U(\lambda ))\rceil \) rounds (rather than for \(\lceil \log _\lambda (B(\lambda )) \rceil \) rounds).
We prove Theorem 6.2 by using the unique VDF \(\mathsf {uVDF} \) from Sect. 5 as a building block. We start with some definitions which will be helpful in the construction.
Definition 6.5
(Puzzle tree). A \((\mathsf {pp} _{\mathsf {uVDF}},d',g)\)-puzzle tree for \(\mathsf {pp} _{\mathsf {uVDF}} = (N, B, k, d, \mathsf {hash}) \) is a \((k+1)\)-ary tree that has the following syntax.
-
Each node is labeled by a string \(s \in \left\{ 0,1,\ldots ,k\right\} ^{*}\), where the root is labeled with the empty string \(\mathsf {null}\), and for a node labeled s, its ith child is labeled s||i for \(i \in \left\{ 0,1,\ldots ,k\right\} \). We let \([s]_{i}\) denote the ith character of s for \(i \in \mathbb {N} \).Footnote 15
-
We define the height of the tree as \(h = \lceil \log _{k}(B) \rceil - d'\) which determines difficulty at each node. Specifically, each node s is associated with the difficulty \(t = k^{h +d'-\left| s \right| }\).Footnote 16
-
Each node s has a value \(\mathsf {val} (s) = (x,y,\pi )\), where we call x the input, \(y\) the output, and \(\pi \) the proof.
The inputs, outputs, and proofs of each node are defined as follows:
-
The root has input g. In general, for a node s with input x and difficulty t, its first k children are called segment nodes and its last child is called a sketch node. Each segment node s||i has input
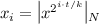 and the sketch node s||k has input \(x'\) where \((x',*) = \mathsf {Sketch} (\mathsf {pp} _{\mathsf {uVDF}},(x,t),x_{k},(x_{1},\ldots ,x_{k-1}))\) (given in Fig. 3).
and the sketch node s||k has input \(x'\) where \((x',*) = \mathsf {Sketch} (\mathsf {pp} _{\mathsf {uVDF}},(x,t),x_{k},(x_{1},\ldots ,x_{k-1}))\) (given in Fig. 3). -
For a node s with input x and difficulty t, its output and proof are given by \((y, \pi ) = \mathsf {uVDF}.\mathsf {Eval}(\mathsf {pp} _{\mathsf {uVDF}},(x,t))\).
We note that whenever we refer to a node s, we mean the node labeled by s, and when we refer to a pair \((s',\mathsf {value})\), this corresponds to a node and associated value (where \(\mathsf {value} \) may not necessarily be equal to the true value \(\mathsf {val} (s)\)).
Definition 6.6
(Left/Middle/Right Nodes). For a node with label s in a \((\mathsf {pp} _{\mathsf {uVDF}},d',g)\)-puzzle tree with \(s = s' || i\) for \(i \in \left\{ 0,1,\ldots ,k\right\} \), we call s a leftmost child if \(i=0\), a rightmost child if \(i=k\), and a middle child otherwise. Additionally, we define the left (resp. right) siblings of s to be the set of nodes \(s' || j\) for \(0 \le j < i\) (resp. \(i < j \le k\)).
Next, we define a frontier. At a high level, for a leaf s, the frontier of s will correspond to the state of the continuous VDF upon reaching s. Specifically, it will contain all nodes whose values have been computed at that point, but whose parents’ values have not yet been computed.
Definition 6.7
(Frontier). For a node s in a \((\mathsf {pp} _{\mathsf {uVDF}},d',g)\)-puzzle tree, the frontier of s, denoted \(\mathsf {frontier} (s)\), is the set of pairs \((s',\mathsf {val} (s'))\) for nodes \(s'\) that are left siblings of any of the ancestors of s. We note that s is included as one of its ancestors.Footnote 17
Next, we define what it means for a set to be consistent. At a high level, for a set of nodes and values, consistency ensures that the relationship of their given inputs and outputs across different nodes is in accordance with the definition of a puzzle tree. If a set is consistent, it does not imply that the input-output pairs are correct, but it implies that they “fit” together logically. Note that consistency does not check proofs.
Definition 6.8
(Consistency). Let S be a set of pairs \((s,\mathsf {value})\) for nodes s and values \(\mathsf {value} \) in a \(((N, B, k, d, \mathsf {hash}),d',g)\)-puzzle tree. We say that \((s',(x,y))\) is consistent with S if the following hold:
-
1.
The input x of \(s'\) is (a) the output given for its left sibling if its left sibling is in S and \(s'\) is a middle child, (b) given by the sketch of its left siblings’ values if all of its left siblings are in S and \(s'\) is a rightmost child, or (c) defined recursively as its parent’s input if \(s'\) is a leftmost child (where the base of the recursion is the root with input g).
-
2.
The output y of \(s'\) is (a) given by the sketch of its left siblings’ values if all of its left siblings are in S and \(s'\) is a rightmost child, or (b) given recursively by its parent’s output if \(s'\) is a kth child (where, upon reaching the root recursively, we then accept any output for \(s'\)).
We say that S is a consistent set if every node in S is consistent with S.
6.1 Construction
Before giving the cVDF construction, we give a detailed overview. At a high level, the cVDF will iteratively compute each leaf node in a \((\mathsf {pp} _{\mathsf {uVDF}},d',g)\)-puzzle tree, where \(\mathsf {pp} _{\mathsf {uVDF}} = (N, B, k, d, \mathsf {hash}) \) are the public parameters of the underlying uVDF and g is the starting point of the tree given by \(\mathsf {uVDF}\).\(\mathsf {Sample}\).
The heart of our construction is the \(\mathsf {cVDF}.\mathsf {Eval}\) functionality which takes a state v corresponding to a leaf s in the tree and computes the next state \(v'\) corresponding to the next leaf. Each state v will be of the form (g, s, F), where s is the current leaf in the tree and F is the frontier of s. Then, \(\mathsf {cVDF}.\mathsf {Eval}(1^\lambda ,\mathsf {pp},(g,s, \mathsf {frontier} (s))\) will output \((g,s+1,\mathsf {frontier} (s+1))\). There are three phases of the algorithm \(\mathsf {cVDF}.\mathsf {Eval}\). First, it checks that its input is well-formed. It then computes \(\mathsf {val} (s)\) using \(\mathsf {frontier} (s)\), and then computes \(\mathsf {frontier} (s+1)\) using both \(\mathsf {frontier} (s)\) and \(\mathsf {val} (s)\). These are discussed next.
Checking That \(\varvec{v}\) Is Well-Formed. Recall that \(v = (g,s,F)\) corresponds to the node s in the tree. This state v is correct if running \(\mathsf {cVDF}.\mathsf {Eval}\) for s steps (where s is interpreted as an integer in base \((k+1)\)) starting at the leaf \(0^{h}\) results in \((g,s,\mathsf {frontier} (s))\). Therefore, before computing the next state, \(\mathsf {cVDF}.\mathsf {Eval}\) needs to verify that the state it was given is correct. To do this, we run \(\mathsf {cVDF}.\mathsf {Verify} \) with input state \((g,0^{h},\bot )\) and output state (g, s, F), and check that this is s steps of computation.
Computing the Value of \(\varvec{s}\). To compute \(\mathsf {val} (s)\), we have the following observation: for every node, its input is a function of the input of its parent and the outputs of its left siblings. Indeed, if s is a middle child, its input is the output of the sibling to its left (given in F). If s is a rightmost child, its input is the sketch of the values of its left siblings (also given in F). If s is a leftmost child, its input is input of its parent, defined recursively. Therefore, we compute its input based on F in this manner. Then, we compute its output by running \(\mathsf {uVDF}.\mathsf {Eval}\) on its input (Fig. 4).
Computing the Frontier of \(\varvec{s+1}\). The final phase of \(\mathsf {cVDF}.\mathsf {Eval}\) is to compute the next frontier using \(\mathsf {val} (s)\) and \(\mathsf {frontier} (s)\). To do this, we consider the closest common ancestor a of s and \(s+1\) and note that by definition, \(\mathsf {frontier} (a) \subset \mathsf {frontier} (s+1)\). Moreover, its straightforward to see that \(\mathsf {frontier} (s+1) \setminus \mathsf {frontier} (a)\) only contains a node \(a^{\star }\) and its left siblings, where \(a^{\star }\) is the child of a along the path to s. Note that when s and \((s+1)\) are siblings, then \(a^{\star } = s\), and otherwise, it can be shown that \(a^{\star }\) is the closest ancestor of s that is not a rightmost child.
Therefore, to compute \(\mathsf {frontier} (s+1)\), we start by computing the value of node \(a^{\star }\). If \(a^{\star } = s\), then we have already computed it, and otherwise it’s input and output are known from its children’s values in F. Specifically, its input is the input of its first child, and its output is the output of its kth child. These are in F because of the definition of \(a^{\star }\), which implies that each of its descendants along the path to s must be rightmost children. To compute its proof, observe that the values of s and its siblings are all known, so they can be efficiently merged into a proof of its parent. If the parent is \(a^{\star }\), then we are done. If not, we can similarly merge values into a proof of the grandparent of s. We can continue this process until we reach \(a^{\star }\). We show how to do this by traversing the path from s up to \(a^{\star }\) and by iteratively “merging” values up the tree. An example depicting \(s,s+1,a,a^{\star }\) is given in Fig. 4.
An example of computing \(\mathsf {frontier} (s+1)\) from \(\mathsf {frontier} (s)\) for \(k=2\) with nodes s, \(s+1\), \(a^{\star }\), and a given. In both graphs, the yellow node is the current node at that point in the computation, and the nodes in gray are those whose proofs have already been merged to proofs at their parents. In the left graph, the frontier of s is shown in pink. The right graph is the result of merging values to obtain the frontier of \(s'\), which is shown in blue. (Color figure online)
Formal construction. Next, we give the formal details of our construction \(\mathsf {cVDF} = (\mathsf {cVDF}.\mathsf {Gen}, \mathsf {cVDF}.\mathsf {Sample}, \mathsf {cVDF}.\mathsf {Eval}, \mathsf {cVDF}.\mathsf {Verify})\).
-
\(\mathsf {pp} \leftarrow \mathsf {cVDF}.\mathsf {Gen} (1^\lambda )\) :
Sample \(\mathsf {pp} _{\mathsf {uVDF}} \leftarrow \mathsf {uVDF}.\mathsf {Gen} (1^\lambda )\) where \(\mathsf {pp} _{\mathsf {uVDF}} = (N, B, k, d, \mathsf {hash}) \). Let \(d'\) be a constant, which will be specified in the proof of iterative sequentiality (in the full version), and set tree height \(h = \lceil \log _{k}(B) \rceil -d'\). Output \(\mathsf {pp} =(\mathsf {pp} _{\mathsf {uVDF}},d',h)\).
-
\(v \leftarrow \mathsf {cVDF}.\mathsf {Sample} (1^\lambda ,\mathsf {pp})\) :
Sample \(g \leftarrow \mathsf {uVDF}.\mathsf {Sample} (1^\lambda ,\mathsf {pp} _{\mathsf {uVDF}})\) and output \(v = (g,0^{h},\emptyset ) \).
-
\(v' \leftarrow \mathsf {cVDF}.\mathsf {Eval}(1^\lambda ,\mathsf {pp},v)\) :
Check that \(\varvec{v}\) is well-formed:
-
1.
Parse v as (g, s, F), where s is a leaf label in a \((\mathsf {pp} _{\mathsf {uVDF}},g)\)-puzzle tree and F is a frontier. Output \(\bot \) if v cannot be parsed this way.
-
2.
Run \(\mathsf {cVDF}.\mathsf {Verify} (1^\lambda ,\mathsf {pp},((g,0^{h},\emptyset ),s),(g,s,F))\) to verify v. Output \(\bot \) if it rejects.
-
1.
Compute the value of \(\varvec{s}\) :
-
1.
Compute the input x of node s as the output of the sibling to its left (given in F) if s is a middle child, a sketch of its left siblings’ values (given in F) if s is a rightmost child, or recursively as its parent’s input if s is a leftmost child.
-
2.
Compute its output and proof as \((y,\pi ) = \mathsf {uVDF}.\mathsf {Eval}(1^\lambda ,\mathsf {pp} _{\mathsf {uVDF}},(x,k^{d'}))\).
Compute the frontier of \(\varvec{s+1}\) :
-
1.
Let a be the closest common ancestor of s and \(s+1\), and let \(a^{\star }\) be the ancestor of s that is a child a.
-
2.
If \(a^{\star } = s\), compute its value as \((x^{\star },y^{\star },\pi ^{\star }) = (x,y,\pi )\).
-
3.
If \(a^{\star }\) is a strict ancestor of s, let \(x^{\star }\) be the input of its leftmost child in F, let \(y^{\star }\) be the output of its kth child in F, and let \(\pi ^{\star }\) be \(\bot \) if \(x^{\star }\) is invalid and otherwise the outputs of its first \(k-1\) children in F along with the proof, computed recursively, of its child along the path to s.
-
4.
Form the next frontier \(F'\) by removing all descendants of \(a^{\star }\) from F, and adding \((a^{\star }, (x^{\star },y^{\star },\pi ^{\star }))\).
Finally, output \((g,s+1, F')\).
-
\(b \leftarrow \mathsf {cVDF}.\mathsf {Verify} (1^\lambda ,\mathsf {pp},(v,T),v')\) :
Check that \(\varvec{v}\) is well-formed:
Parse v as (g, s, F) where \(g \in \mathbb {Z} _{N}^{\star } \), s is a leaf node, and F is a frontier. If v cannot be parsed this way, then output 1 if \(v' = \bot \) and 0 otherwise.
If \((g,s,F) \ne (g,0^{h},\emptyset ) \), then verify the state v by recursively running this verification algorithm, i.e., \(\mathsf {cVDF}.\mathsf {Verify} (1^\lambda ,\mathsf {pp},((g,0^{h},\emptyset ),s),(g,s,F))\). If this rejects, then output 1 if \(v' = \bot \) and 0 otherwise.
Check that \(\varvec{v'}\) is correct:
Output 1 if the following checks succeed, and 0 otherwise:
-
1.
Parse \(v'\) as \((g,s+T,F')\) where \(F'\) is a frontier.
-
2.
Check that the set of nodes in \(F'\) is the set of nodes in \(\mathsf {frontier} (s')\) (considering only node labels and not values).
-
3.
Check that \(F'\) is a consistent set.Footnote 18
-
4.
For each element \((s',(x,y,\pi )) \in F'\), check that \(\mathsf {uVDF}.\mathsf {Verify} (1^\lambda ,\mathsf {pp} _{\mathsf {uVDF}}, (x,t),(y,\pi ))\) accepts, where \(t = k^{h +d'-\left| s' \right| }\).
-
1.
Theorem 6.9
Let \(D,B :\mathbb {N} \rightarrow \mathbb {N} \) where \(B(\lambda ) \le 2^{\lambda ^{1/3}}\), \(D(\lambda ) = \lambda ^{d'}\) for all \(\lambda \in \mathbb {N} \) and specific constant \(d'\). Assume that (1) the (D, B)-RSW assumption holds for an \(\epsilon \in (0,1)\) and a polynomial \(\ell \), and (2) for any constants \(\epsilon ',\delta \in (0,1)\), \(\mathsf {uVDF} \) (given in Sect. 5) is a \((D,B, (1+\delta )\cdot \ell , \epsilon ')\)-unique VDF. Then \(\mathsf {cVDF} \) is a \((B,(1+\delta ') \cdot D \cdot \ell , \epsilon '')\)-cVDF for any \(\epsilon '' > \frac{\epsilon + \delta '}{1+\delta '}\) and \(\delta ' > \delta \).
The proof is deferred to the full version. As a corollary, by combining Theorem 5.2 with Theorem 6.9, we obtain Theorem 6.2: a continuous VDF under the Fiat-Shamir and the repeated squaring assumptions.
Notes
- 1.
- 2.
If g is perfectly iteratively sequential, meaning that t iterations cannot be computed in time faster than exactly \(t \cdot \ell \), then after t steps of g the next value would be unpredictable. However, if t iterations cannot be computed in time faster than \((1-\epsilon ) \cdot t \cdot \ell \), we can only guarantee that the \((\epsilon \cdot t)\)-th value into the future is unpredictable.
- 3.
Our notion of a cVDF (just like the earlier notion of a “plain” VDF) also allows for the existence of some trusted public parameters.
- 4.
Although, [40] shows that it does hold in the random oracle model for his particular protocol.
- 5.
As mentioned above, in general, the Fiat-Shamir assumption is false for super-constant-round proofs. But we state a restricted form of a Fiat-Shamir assumption for super-constant-round proofs with exponentially small soundness error which holds in the random oracle model, due to the classic reduction from [26].
- 6.
We also note that Choudhuri et al. show how to instantiate the hash function in their Fiat-Shamir transformation assuming a class of fully homomorphic encryption schemes has almost-optimal security against quasi-polynomial time adversaries. We leave such instantiations in our context for future work.
- 7.
If we additionally assume that the repeated squaring assumption is sub-exponentially hard, then the resulting instance cannot be solved in depth \(n^{c/d}\) and sub-exponential time.
- 8.
Giving the square root x is the cause of our computational uniqueness guarantee, since a different square root for \(x^{2}\) would verify. As mentioned, working over \(\mathsf {QR}_{N} ^{+}\) would prevent this attack and give information theoretic uniqueness, as in [40].
- 9.
We thank the anonymous EUROCRYPT reviewers for pointing out that Pietrzak’s protocol satisfies adaptive soundness using \(\mathsf {QR}_{N} ^{+}\).
- 10.
The name sketch is inspired by the notion of a sketch in algorithms, which refers to a random linear projection.
- 11.
We are talking about an instantiation of the VDF in the plain model using a concrete hash function. The resulting VDF is provably secure in the random oracle model for any k.
- 12.
- 13.
The assumption is usually called the RSW assumption after Rivest, Shamir, and Wagner who used it to construct time-lock puzzles [43].
- 14.
We note that \(x_{0}\) uniformly from \(\mathbb {Z} _{N}^{\star } \) is sufficient due to the following. By Fact 3.6, it holds that \(\mathsf {uVDF}.\mathsf {Sample} \) will succeed whenever \(\langle x_{0}^{2} \rangle = \mathsf {QR}_{N} \). Furthermore, \(x_{0}^{2}\) is a random element of \(\mathsf {QR}_{N} \), and therefore is a generator with probability \(1 - (p' + q')/(p' \cdot q') \ge 1 - 4/2^{\lambda }\). Also note that \(x_{0}\) is distributed according to \(\mathsf {RSW}.\mathsf {Sample} (1^\lambda ,N)\).
- 15.
For ease of notation, we store s as a \((k+1)\)-ary string and when doing integer operations, they are implicitly done in base \((k+1)\).
- 16.
Note that since the tree has height \(h \), this implies that each leaf has difficulty \(t = k^{d'}\).
- 17.
It may be helpful to observe that for a leaf node \(s = [s]_{1} || [s]_{2} || \cdots || [s]_{h}\), the frontier contains \([s]_{i}\) nodes at level i for \(i \in [h ]\).
- 18.
This can be done efficiently, since consistency of every element in \(F'\) can be checked by looking at k nodes in each of the \(h \) levels of the tree and performing at most one sketch.
References
Chia network. https://chia.net/. Accessed 17 May 2019
Ethereum foundation. https://www.ethereum.org/. Accessed 17 May 2019
Protocol labs. https://protocol.ai/. Accessed 17 May 2019
VDF research effort. https://vdfresearch.org/. Accessed 17 May 2019
Abbot, T., Kane, D., Valiant, P.: On algorithms for Nash equilibria (2004). http://web.mit.edu/tabbott/Public/final.pdf. Accessed 18 Sept 2019
Barak, B.: How to go beyond the black-box simulation barrier. In: 42nd IEEE Symposium on Foundations of Computer Science, FOCS, pp. 106–115 (2001)
Bennett, C.H.: Time/space trade-offs for reversible computation. SIAM J. Comput. 18(4), 766–776 (1989)
Bitansky, N., Goldwasser, S., Jain, A., Paneth, O., Vaikuntanathan, V., Waters, B.: Time-lock puzzles from randomized encodings. In: Innovations in Theoretical Computer Science, ITCS, pp. 345–356 (2016)
Bitansky, N., Paneth, O., Rosen, A.: On the cryptographic hardness of finding a Nash equilibrium. In: Guruswami, V. (ed.) IEEE 56th Symposium on Foundations of Computer Science, FOCS, pp. 1480–1498 (2015)
Boneh, D., Bonneau, J., Bünz, B., Fisch, B.: Verifiable delay functions. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 757–788. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_25
Boneh, D., Bünz, B., Fisch, B.: A survey of two verifiable delay functions. IACR Cryptology ePrint Archive 2018, 712 (2018)
Boneh, D., Naor, M.: Timed commitments. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 236–254. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_15
Cai, J., Lipton, R.J., Sedgewick, R., Yao, A.C.: Towards uncheatable benchmarks. In: 8th Structure in Complexity Theory Conference, pp. 2–11. IEEE Computer Society (1993)
Chen, X., Deng, X., Teng, S.: Settling the complexity of computing two-player Nash equilibria. J. ACM 56(3), 14:1–14:57 (2009)
Choudhuri, A.R., Hubáček, P., Kamath, C., Pietrzak, K., Rosen, A., Rothblum, G.N.: Finding a Nash equilibrium is no easier than breaking Fiat-Shamir. In: 51st ACM SIGACT Symposium on Theory of Computing, STOC, pp. 1103–1114 (2019)
Choudhuri, A.R., Hubáček, P., Kamath, C., Pietrzak, K., Rosen, A., Rothblum, G.N.: PPAD-hardness via iterated squaring modulo a composite. IACR Cryptology ePrint Archive 2019, 667 (2019)
Chung, K., Lin, H., Pass, R.: Constant-round concurrent zero knowledge from P-certificates. In: 54th IEEE Symposium on Foundations of Computer Science, FOCS, pp. 50–59 (2013)
Cohen, B., Pietrzak, K.: Simple proofs of sequential work. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 451–467. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_15
Daskalakis, C., Goldberg, P.W., Papadimitriou, C.H.: The complexity of computing a Nash equilibrium. Commun. ACM 52(2), 89–97 (2009)
Döttling, N., Garg, S., Malavolta, G., Vasudevan, P.N.: Tight verifiable delay functions. IACR Cryptology ePrint Archive 2019, 659 (2019)
Döttling, N., Lai, R.W.F., Malavolta, G.: Incremental proofs of sequential work. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 292–323. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_11
Dwork, C., Naor, M.: Pricing via processing or combatting junk mail. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 139–147. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_10
De Feo, L., Masson, S., Petit, C., Sanso, A.: Verifiable delay functions from supersingular isogenies and pairings. IACR Cryptology ePrint Archive 2019, 166 (2019)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Garg, S., Pandey, O., Srinivasan, A.: Revisiting the cryptographic hardness of finding a nash equilibrium. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 579–604. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_20
Goldreich, O., Krawczyk, H.: On the composition of zero-knowledge proof systems. In: Paterson, M.S. (ed.) ICALP 1990. LNCS, vol. 443, pp. 268–282. Springer, Heidelberg (1990). https://doi.org/10.1007/BFb0032038
Goldwasser, S., Kalai, Y.T.: On the (in)security of the Fiat-Shamir paradigm. In: 44th IEEE Symposium on Foundations of Computer Science, FOCS, pp. 102–113 (2003)
Hubáček, P., Yogev, E.: Hardness of continuous local search: query complexity and cryptographic lower bounds. In: 28th ACM-SIAM Symposium on Discrete Algorithms, SODA, pp. 1352–1371 (2017)
Jerschow, Y.I., Mauve, M.: Non-parallelizable and non-interactive client puzzles from modular square roots. In: 6th International Conference on Availability, Reliability and Security, ARES1, pp. 135–142. IEEE Computer Society (2011)
Kaliski, B.: PKCS #5: password-based cryptography specification version 2.0 (2000)
Kitagawa, F., Nishimaki, R., Tanaka, K.: Obfustopia built on secret-key functional encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 603–648. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_20
Komargodski, I., Segev, G.: From Minicrypt to Obfustopia via private-key functional encryption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 122–151. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_5
Lenstra, A.K., Wesolowski, B.: Trustworthy public randomness with sloth, unicorn, and trx. IJACT 3(4), 330–343 (2017)
Lin, H., Pass, R., Soni, P.: Two-round and non-interactive concurrent non-malleable commitments from time-lock puzzles. In: 58th IEEE Symposium on Foundations of Computer Science (FOCS), pp. 576–587 (2017)
Lund, C., Fortnow, L., Karloff, H.J., Nisan, N.: Algebraic methods for interactive proof systems. J. ACM 39(4), 859–868 (1992)
Mahmoody, M., Moran, T., Vadhan, S.P.: Publicly verifiable proofs of sequential work. In: Innovations in Theoretical Computer Science, ITCS, pp. 373–388 (2013)
Mahmoody, M., Smith, C., Wu, D.J.: A note on the (im)possibility of verifiable delay functions in the random oracle model. ePrint p. 663 (2019)
Megiddo, N., Papadimitriou, C.H.: On total functions, existence theorems and computational complexity. Theor. Comput. Sci. 81(2), 317–324 (1991)
Papadimitriou, C.H.: On the complexity of the parity argument and other inefficient proofs of existence. J. Comput. Syst. Sci. 48(3), 498–532 (1994)
Pietrzak, K.: Simple verifiable delay functions. In: 10th Innovations in Theoretical Computer Science Conference, ITCS, pp. 60:1–60:15 (2019)
Rabin, M.O.: Digitalized signatures and public key functions as intractable as factoring. Technical report, TR-212, LCS, MIT, Cambridge, MA (1979)
Rabin, M.O.: Transaction protection by beacons. J. Comput. Syst. Sci. 27(2), 256–267 (1983)
Rivest, R.L., Shamir, A., Wagner, D.A.: Time-lock puzzles and timed-release crypto (1996, manuscript)
Valiant, P.: Incrementally verifiable computation or proofs of knowledge imply time/space efficiency. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 1–18. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_1
Wesolowski, B.: Efficient verifiable delay functions. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 379–407. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_13
Zhandry, M.: The magic of ELFs. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 479–508. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_18
Acknowledgements
We thank Ian Miers for suggesting the name continuous VDFs and Eylon Yogev for discussions regarding our PPAD hardness results.
This work was supported in part by NSF Award SATC-1704788, NSF Award RI-1703846, AFOSR Award FA9550-18-1-0267, and by NSF Award DGE-1650441. This research is based upon work supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via 2019-19-020700006. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of ODNI, IARPA, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes notwithstanding any copyright annotation therein.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Ephraim, N., Freitag, C., Komargodski, I., Pass, R. (2020). Continuous Verifiable Delay Functions. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12107. Springer, Cham. https://doi.org/10.1007/978-3-030-45727-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-45727-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45726-6
Online ISBN: 978-3-030-45727-3
eBook Packages: Computer ScienceComputer Science (R0)





 .
. and output
and output  for
for 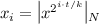 and the sketch node s||k has input
and the sketch node s||k has input 
