Abstract
We propose a renormalization group (RG) theory of eigen microstates, which are introduced in the statistical ensemble composed of microstates obtained from experiments or computer simulations. A microstate in the ensemble can be considered as a linear superposition of eigen microstates with probability amplitudes equal to their eigenvalues. Under the renormalization of a factor b, the largest eigenvalue σ1 has two trivial fixed points at low and high temperature limits and a critical fixed point with the RG relation 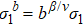 , where β and ν are the critical exponents of order parameter and correlation length, respectively. With the Ising model in different dimensions, it has been demonstrated that the RG theory of eigen microstates is able to identify the critical point and to predict critical exponents and the universality class. Our theory can be used in research of critical phenomena both in equilibrium and non-equilibrium systems without considering the Hamiltonian, which is the foundation of Wilson's RG theory and is absent for most complex systems.
, where β and ν are the critical exponents of order parameter and correlation length, respectively. With the Ising model in different dimensions, it has been demonstrated that the RG theory of eigen microstates is able to identify the critical point and to predict critical exponents and the universality class. Our theory can be used in research of critical phenomena both in equilibrium and non-equilibrium systems without considering the Hamiltonian, which is the foundation of Wilson's RG theory and is absent for most complex systems.
Export citation and abstract BibTeX RIS
In systems consisting of many components (atoms, molecules, electrons, spins, etc.), one of the most striking phenomena is the emergence of diverse types of collective behavior, i.e., phases.[1,2] Under slight changes of external conditions, the systems may have dramatic structural rearrangements, i.e., phase transitions. An emergent phase is characterized by the so-called order parameter, which was introduced by Landau.[3] In association with continuous change or discontinuous jump of order parameter at the transition point, the phase transition is continuous or discontinuous.
Near the transition point of a continuous phase transition, the correlation length ξ is much larger than the microscopic length scale 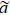 . Hence,
. Hence, 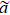 becomes irrelevant and ξ is the only important length scale. The critical behaviors of system are governed by fluctuations that are statistically self-similar up to ξ. Kadanoff took advantage of this self-similarity and introduced the block spin scaling that gradually eliminates the correlated degrees of freedom at length scales r ≪ ξ.[4] The major breakthrough in the theory of critical phenomena came with the renormalization group (RG) theory of Wilson[5,6] and co-workers,[7,8] which is based on the similarity of Hamiltonian during the renormalization. The RG theory has been well established and its theoretical predictions have been verified by experiments under the low-gravity environment of space.[9]
becomes irrelevant and ξ is the only important length scale. The critical behaviors of system are governed by fluctuations that are statistically self-similar up to ξ. Kadanoff took advantage of this self-similarity and introduced the block spin scaling that gradually eliminates the correlated degrees of freedom at length scales r ≪ ξ.[4] The major breakthrough in the theory of critical phenomena came with the renormalization group (RG) theory of Wilson[5,6] and co-workers,[7,8] which is based on the similarity of Hamiltonian during the renormalization. The RG theory has been well established and its theoretical predictions have been verified by experiments under the low-gravity environment of space.[9]
The RG theory of critical phenomena has elucidated the mathematical mechanism for scaling and universality which states that all phase transitions can be divided into several distinct classes.[10] Within a given class, all critical points have the same asymptotic behaviors.[10] For very different systems (e.g., fluids and magnets) within a given class, there is the so-called two-scale factor universality so that the asymptotic critical behavior is believed to be known completely provided that two nonuniversal amplitudes are given.[11–15] However, it is proved by the RG of the O(n) symmetric ϕ4 field theory with the spatially anisotropic Hamiltonian that the two-scale factor universality is valid for isotropic systems like fluids but not for anisotropic systems.[16] This new finding is of special importance since the anisotropy exists widely in real systems.[17] The predicted dependence of the critical Binder cumulant on the anisotropy has been confirmed by the Monte Carlo studies of the Ising models.[18,19]
Nowadays, we need to study urgently the critical phenomena of complex systems without knowledge of their Hamiltonian.[20,21] Recently, we proposed an eigen microstate approach (EMA)[22,23] based on microstates obtained from experiments or simulations. The statistical ensemble composed of the microstates during an observation time period is described by a normalized matrix. From this matrix we can calculate eigen microstates. Now, we can consider a microstate as a linear superposition of eigen microstates with probability amplitudes equal to the corresponding eigenvalues. A finite eigenvalue in the thermodynamic limits indicates the condensation of eigen microstate and the emergence of a phase described by the eigen microstate. This approach is a generalization of the Bose–Einstein condensation of Bose gas and can be used to study phase transitions of broad interests. The order parameter of phase transition is identified naturally as the eigenvalue, which follows a finite-size scaling scaling form in the critical region. According to the finite-size scaling form, we can calculate critical exponents of a phase transition and fix its universality class. The EMA has been applied successfully to study the equilibrium phase transitions of the Ising model[22,23] and the Viscek model of the non-equilibrium collective motion.[24] In addition, we have used EMA to investigate global temperature fluctuations of the Earth[23] and spatial distribution of ozone at different geopotential heights,[25] based on empirical data.
In this Letter, we propose the RG theory of eigen microstates. First, we summarize the RG theory of Wilson based on the Hamiltonian in the following.
We consider the Ising model on a d-dimensional lattice with size L and lattice spacing 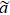 . Its Hamiltonian can be written as
. Its Hamiltonian can be written as
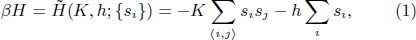
where β = 1/kB T, si = ±1, and h is the external field. Its partition function can be calculated as

All thermodynamic quantities can be obtained from this partition function.
In the RG theory, the first step is to decrease the resolution by changing the minimum length scale from 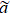 to
to 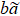 , where b > 1. The cell of size
, where b > 1. The cell of size 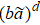 has NI
= bd
spins and 2N
I
microstates. We divide the 2N
I
microstates into two groups, which are represented by σI
and have cell spin SI
= ±1. All spins of the system can be expressed from {si
} to {SI
, σI
}. In the calculation of partition function, we consider first the contributions of all σI
for a set of cell spins {SI
} and have
has NI
= bd
spins and 2N
I
microstates. We divide the 2N
I
microstates into two groups, which are represented by σI
and have cell spin SI
= ±1. All spins of the system can be expressed from {si
} to {SI
, σI
}. In the calculation of partition function, we consider first the contributions of all σI
for a set of cell spins {SI
} and have

where Kb is related to the interaction between cell spins and hb is the external field acting on cell spins.
The free energy density takes the form

where V = Ld , Vb = (L/b)d . The singular part of free energy density follows the relation
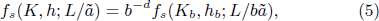
where Kb and hb follow the RG transforms


These transforms have two trivial fixed points:
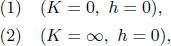
which correspond to high temperature limit T = ∞ and low temperature limit T = 0, respectively.
In addition, there is a non-trivial fixed point (K = K*, h = 0), which corresponds to a critical point. Near this fixed point with small δK = K – K* and δh = h, we have the RG transforms


The reduced temperature t = (K* – K)/K* is related to δK as t = –δK/K*.
At h = 0, the correlation length approaches infinity with t → 0 in power law as ξ(t) = ξ0 t–ν . At t = 0, the correlation length goes to infinity with h → 0 as ξh (h) = ξ0 h h–ν h . After the renormalization with factor b, the system is taken away from the critical point with smaller correlation lengths ξ(tb ) = ξ(t)/b and ξh (hb ) = ξh (h)/b. Then we have tb = b1/ν t and hb = b1/νh h. Using the RG transforms of Eqs. (8) and (9), we obtain the critical exponents


We rewrite the singular part of free energy density as functions of t and h and have
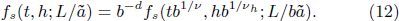
The order parameter, susceptibility, and specific heat can be calculated by the derivatives of fs with respect to h and t as
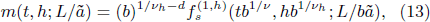

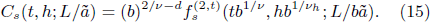
After taking h = 0 and the limit L → ∞, we choose b ∝ t–ν for t > 0 and b ∝ (–t)–ν for t < 0. Then we obtain the bulk order parameter
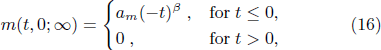
with β = dν – ν/νh , the bulk susceptibility
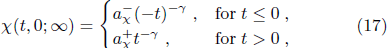
with γ = 2ν/νh – dν, and the bulk specific heat
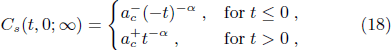
with α = 2 – dν.
The critical behaviors of thermodynamic quantities are essentially realized by the divergence of correlation length ξ when approaching the critical point. The clusters composed of the correlated components possess the sizes proportional to ξd
. The reduced critical exponents of thermodynamic quantities with respect to ξd
are more essential. They are  ,
, 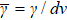 , and
, and 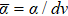 , etc. The critical exponents of ξd
are
, etc. The critical exponents of ξd
are 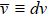 and
and 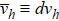 . Now, the reduced critical exponents depend only on
. Now, the reduced critical exponents depend only on 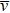 and
and 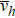 as
as 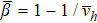 ,
, 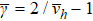 , and
, and 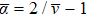 .
.
For the Ising model on d-dimensional lattice, ν = 1.0, 0.63012(16),[26] and 0.5 for d = 2, 3, and 4, respectively. Correspondingly, we have 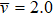 , 1.89036(48), 2.0, which show a weak dependence on dimension d. In the bond percolation on one- and two-dimensional lattices with long-range connection probability P (r) ∝ r–(d + σ) for σ < 0, it was found that
, 1.89036(48), 2.0, which show a weak dependence on dimension d. In the bond percolation on one- and two-dimensional lattices with long-range connection probability P (r) ∝ r–(d + σ) for σ < 0, it was found that 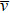 keeps to be the same.[27]
keeps to be the same.[27]
Now, we rewrite the singular part of free energy as
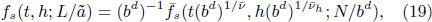
where 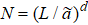 . Then we obtain the RG transformation of the thermodynamic functions as follows:
. Then we obtain the RG transformation of the thermodynamic functions as follows:
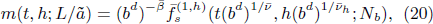
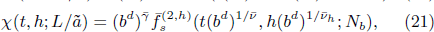
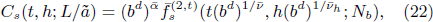
where Nb = N/bd . With bd = N and Nb = 1, we can reach the finite-size scaling form[28]
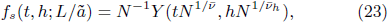
and the thermodynamic quantities
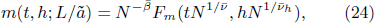
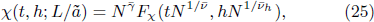
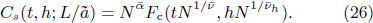
As pointed out above, the RG theory of Wilson[5,6] cannot be applied to the systems whose Hamiltonian is unknown. To be able to study the critical phenomena of these systems, we develop here the RG theory of eigen microstates.
The EMA developed by us[23,24] follows the concept of statistical ensemble, which was introduced by Gibbs in 1902.[29] The statistical ensemble is composed of microstates of a system, which are defined by the states of individuals in the system. Gibbs proposed to describe the statistical ensemble by the probability density of microstate. For equilibrium systems under three different thermodynamic conditions, the microcanonical, canonical, and grand canonical probability densities of microstate were given by Gibbs.[29] The thermodynamic properties of equilibrium system with known energy function can be calculated using the probability density of microstate. However, for a lot of complex systems, both energy function and probability density of microstate are unknown. We must go a new way. Instead of caring the energy function and the probability density of microstate, we study the eigen microstates of statistical ensemble to identify the collective and emergent behaviors of system.
We consider a complex system composed of N agents, which have states si (τ) with i = 1,2,..., N and τ = 1,2,..., M. The microstate at time τ is defined as
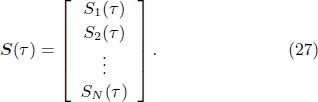
We take M > N microstates to compose a statistical ensemble, which is described by an N × M matrix A with elements

where 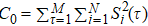 so that Tr (
A
⋅
A
T) = 1.
so that Tr (
A
⋅
A
T) = 1.
From the correlation matrix between agent states K = AA T, we can calculate eigenvectors UI , I = 1, 2, ..., N. The correlation matrix between microstates C = A T A has M eigenvectors VI , I = 1,2,...,M.
According to the singular value decomposition (SVD), the ensemble matrix A can be decomposed as
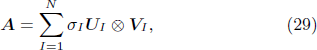
where 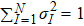 . According to the decomposition, we can consider microstate
S
(τ) as a linear superposition of eigen microstates
UI
by the relation
. According to the decomposition, we can consider microstate
S
(τ) as a linear superposition of eigen microstates
UI
by the relation 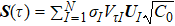 , where σI
is the probability amplitude of
UI
.
, where σI
is the probability amplitude of
UI
.
For complex systems without dominant eigen microstate, all σI → 0 in the limits N → ∞, M → in the limits. With the finite limit of σI there is a condensation of eigen microstate UI , which is similar to the Bose–Einstein condensation of Bose gas. This condensation corresponds to a phase transition with the new phase UI and the order parameter σI .
It is essential in the EMA to define microstates properly in order to catch the relevant properties of a system. The microstates of different systems could be quite different. For the Ising models, microstates are defined by all spins of system.[22,23] In the collective motion of living systems, microstates are described by the neighborhood density fluctuations and the orientations of velocity.[22,23] In studies of the Earth system with EMA, the reduced temperature fluctuations and the ozone's variations are used for microstates respectively.[23,25]
The principal component analysis (PCA) is a algorithm to transform the columns of a dataset into a new set of principal components. After doing this, the information across the full dataset is effectively compressed in fewer principal components. We have applied the PCA to the two-dimensional Ising model and found that the eigenvalues are related to the susceptibility.[30] The spatial distributions of principal components were also investigated.[30] In comparison with the application of PCA, the EMA forces us to define properly the microstates of a system first from the dataset and then compose a statistical ensemble. With the application of the EMA, we can obtain not only the eigen microstates UI , but also their evolutions with time VI and the order parameter σI . The essential and important information of system is contained in VI . As an example, VI of the Earth system is related very closely to the global monsoon and the Oceanic Niño indexes at I = 2 and I = 5, respectively.[23] Thus, VI is very helpful for identifying the features of the eigen microstate UI . Recently, it was attempted to bring the PCA into contact with RG.[31]
It has been confirmed[22–24] that σI
of d-dimensional system with 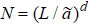 follows the finite-size scaling form
follows the finite-size scaling form
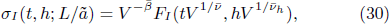
in the asymptotic region |t| ≪ 1, |h| ≪ 1, and 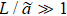 .
.
After the RG transformation with minimum length scale changed from  to
to 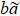 , we define the states of a cell with the size
, we define the states of a cell with the size 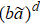 from the states of all agents within the cell. Using the cell states we can obtain then the renormalized microstates
Sb
(τ) and the renormalized ensemble matrix
Ab
. With new eigenvalues
from the states of all agents within the cell. Using the cell states we can obtain then the renormalized microstates
Sb
(τ) and the renormalized ensemble matrix
Ab
. With new eigenvalues 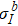 and new eigenvectors
and new eigenvectors 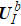 ,
, 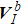 ,
Ab
can be decomposed correspondingly as
,
Ab
can be decomposed correspondingly as
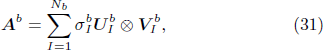
where Nb
= N/bd
and 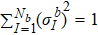 .
.
At high-temperature limit T = ∞, no eigen microstates are dominant and 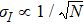 . The eigenvalue
. The eigenvalue 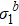 scales as
scales as 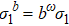 with ω = d/2.
with ω = d/2.
At low-temperature limit T = 0, σ1 = 1. After the RG transformation, we have 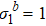 so that
so that 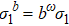 with ω = 0.
with ω = 0.
In the critical region, the eigenvalue after RG transformation becomes
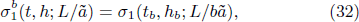
where tb = tb1/ν and hb = hb1/νh .
In the following, we apply the RG theory of eigen microstates to the d-dimensional Ising model with nearest neighbor interaction on square lattice under periodic boundary conditions. The d-dimensional Ising models at d = 3, 2, 1 with 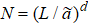 spins are simulated using the Wolff algorithm[32] at different reduced temperatures T = 1/K and external fields h. The bootstrap method is used to get final results and their statistical errors.
spins are simulated using the Wolff algorithm[32] at different reduced temperatures T = 1/K and external fields h. The bootstrap method is used to get final results and their statistical errors.
In Fig. 1 we show the renormalized eigenvalue 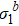 at low and high temperatures of two-dimensional Ising model at h = 0. At low- and hight-temperature limits,
at low and high temperatures of two-dimensional Ising model at h = 0. At low- and hight-temperature limits,  are revealed with ω = 0 and ω = d/2 = 1, respectively.
are revealed with ω = 0 and ω = d/2 = 1, respectively.
Fig. 1. Renormalized eigenvalue 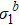 of the two-dimensional Ising model with
of the two-dimensional Ising model with 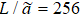 and h = 0 (a) at low temperature and (b) at high temperature, (c) scaling function of
and h = 0 (a) at low temperature and (b) at high temperature, (c) scaling function of 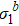 at hight temperature. The error bars of data hereafter are smaller than their symbols.
at hight temperature. The error bars of data hereafter are smaller than their symbols.
Download figure:
Standard imageUsing the scaling form
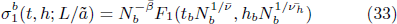
with 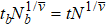 and
and 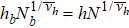 , we can obtain the following RG relation
, we can obtain the following RG relation

Therefore, 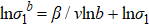 and the log-log plot of
and the log-log plot of 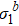 with respect to b is a straight line with slope equal to β/ν. This can be used to identify critical phenomenon and its universality class.
with respect to b is a straight line with slope equal to β/ν. This can be used to identify critical phenomenon and its universality class.
In Fig. 2, the renormalized eigenvalue 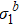 of the two-dimensional Ising model at h = 0 is presented for temperatures near the critical point. We find the straight lines with slope β/ν = 0.1249(3), in agreement with the exact value (β/ν)exact = 0.125. The RG relation of eigen microstate has been confirmed by the Monte Carlo data.
of the two-dimensional Ising model at h = 0 is presented for temperatures near the critical point. We find the straight lines with slope β/ν = 0.1249(3), in agreement with the exact value (β/ν)exact = 0.125. The RG relation of eigen microstate has been confirmed by the Monte Carlo data.
Fig. 2. Renormalized eigenvalue 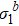 of the two-dimensional Ising model with
of the two-dimensional Ising model with 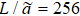 and in the critical region with h = 0: (a) log-log plot of
and in the critical region with h = 0: (a) log-log plot of 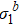 versus b, with the straight line being the best fit to the data, (b)
versus b, with the straight line being the best fit to the data, (b) 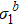 versus T for different b, (c) scaling function of
versus T for different b, (c) scaling function of 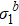 versus T.
versus T.
Download figure:
Standard imageIn Fig. 3, the renormalized eigenvalue 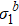 of the two-dimensional Ising model at T = Tc are given for small h in the critical region. Straight lines with slope β/ν are also found. They confirm again the RG relation of eigen microstate.
of the two-dimensional Ising model at T = Tc are given for small h in the critical region. Straight lines with slope β/ν are also found. They confirm again the RG relation of eigen microstate.
Fig. 3. Renormalized eigenvalue  of the two-dimensional Ising model with
of the two-dimensional Ising model with 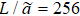 and in the critical region with T = Tc. (a) Log-log plot of
and in the critical region with T = Tc. (a) Log-log plot of 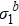 versus b. At different h, data follow different straight lines with the same slope β/ν. (b)
versus b. At different h, data follow different straight lines with the same slope β/ν. (b) 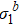 versus h for different b. (c) Scaling function of
versus h for different b. (c) Scaling function of 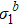 versus h.
versus h.
Download figure:
Standard imageThe eigenvalues σ2 is comparable with σ1 in the critical region[22,23] and there is also the RG relation
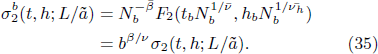
We introduce the ratio
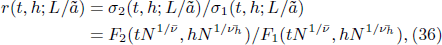
which is unchanged under the renormalization and is universal.
In order to fix critical point precisely, we study the following ratio
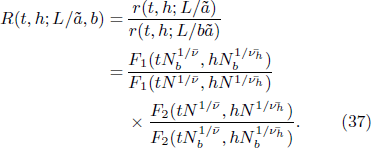
At the critical point with t = 0 and h = hc = 0, R becomes independent of  and b, and Rc = 1. This can be used to determine the critical point easily, by searching for the fixed point of R with respect to b and Rc = 1.
and b, and Rc = 1. This can be used to determine the critical point easily, by searching for the fixed point of R with respect to b and Rc = 1.
In Fig. 4, we present 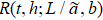 of the two-dimensional Ising model with
of the two-dimensional Ising model with 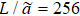 and b = 2,4,8. At hc = 0, there is a fixed point at Tc = 2.269. At T = Tc, there is a fixed point at h = 0.
and b = 2,4,8. At hc = 0, there is a fixed point at Tc = 2.269. At T = Tc, there is a fixed point at h = 0.
Fig. 4. Ratio 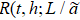 , b) of two-dimensional Ising model with L = 256 and b = 2, 4, 8. (a) At hc = 0, R has a fixed point at Tc = 2.269 and Rc = 1. (b) At T = Tc, R has a fixed point at hc = 0 and Rc = 1.
, b) of two-dimensional Ising model with L = 256 and b = 2, 4, 8. (a) At hc = 0, R has a fixed point at Tc = 2.269 and Rc = 1. (b) At T = Tc, R has a fixed point at hc = 0 and Rc = 1.
Download figure:
Standard imageTo calculate the critical exponents ν and νh , we solve the following equations
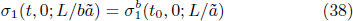
and
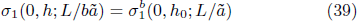
for given t0 and h0 in the critical region. With their solutions 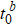 and
and  , we can calculate the critical exponents
, we can calculate the critical exponents
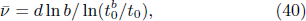
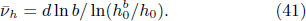
From 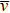 and
and 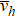 , we can obtain other critical exponents
, we can obtain other critical exponents 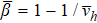 ,
, 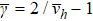 , and
, and 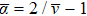 .
.
The solutions 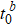 of t0 = 0.01, 0.02, 0.03, 0.04, 0.05 are shown in Fig. 5. It is found that
of t0 = 0.01, 0.02, 0.03, 0.04, 0.05 are shown in Fig. 5. It is found that 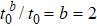 for different t0. Therefore, ν = 1 and
for different t0. Therefore, ν = 1 and 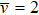 .
.
Fig. 5. Solutions of 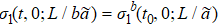 at different t0 for the two-dimensional Ising model. The colorful dash lines depict
at different t0 for the two-dimensional Ising model. The colorful dash lines depict 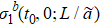 with t0 = 0.01, 0.02, 0.03, 0.04, 0.05. The black circles depict
with t0 = 0.01, 0.02, 0.03, 0.04, 0.05. The black circles depict 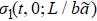 with respect to t.
with respect to t.
Download figure:
Standard imageFor three-dimensional Ising model, the renormalized eigenvalue 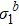 in the critical region with h = 0 is shown in Fig. 6. The RG relation
in the critical region with h = 0 is shown in Fig. 6. The RG relation 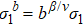 is verified again with β/ν = 0.5199(3), in agreement with the recent Monte Carlo study of high precision.[33]
is verified again with β/ν = 0.5199(3), in agreement with the recent Monte Carlo study of high precision.[33]
Fig. 6. Renormalized eigenvalue 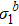 of the three-dimensional Ising model with
of the three-dimensional Ising model with 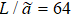 and in the critical region with h = 0. (a) Log-log plot of
and in the critical region with h = 0. (a) Log-log plot of 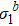 versus b. At different T, data follow different straight lines with the same slope β/ν. (b)
versus b. At different T, data follow different straight lines with the same slope β/ν. (b) 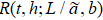 at b = 2, 4, having a cross point at Tc = 4.5115. (c)
at b = 2, 4, having a cross point at Tc = 4.5115. (c) 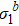 with respect to T for different b. (d) Scaling function of
with respect to T for different b. (d) Scaling function of 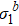 versus T.
versus T.
Download figure:
Standard imageIn the one-dimensional Ising model, the correlation length ξ goes to infinity with T → 0 as ![$\xi =\mathop{a}\limits^{\sim }{(\mathrm{ln}\,[\coth (1/T)])}^{-1}$](https://content.cld.iop.org/journals/0256-307X/39/8/080503/revision2/cpl_39_8_080503_ieqn85.gif) .[34] The susceptibility
.[34] The susceptibility  indicates that
indicates that 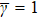 [22,35] and
[22,35] and  .[34]
.[34]
In Fig. 7, we can see that the renormalized eigenvalue 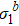 of the one-dimensional Ising model follows the RG relation at low temperature and deviates from this relation when T becomes higher.
of the one-dimensional Ising model follows the RG relation at low temperature and deviates from this relation when T becomes higher.
Fig. 7. Renormalized eigenvalue 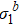 of the one-dimensional Ising model with
of the one-dimensional Ising model with 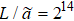 and h = 0. The insets show the trivial fixed point at high temperature with ω = 1/2.
and h = 0. The insets show the trivial fixed point at high temperature with ω = 1/2.
Download figure:
Standard imageIn summary, we have developed the RG theory of eigen microstates for studying critical phenomena of complex systems. In the statistical ensemble composed of microstates obtained from experiments or computer simulations of complex system, a microstate can be considered as a linear superposition of eigen microstates with probability amplitudes equal to the corresponding eigenvalues. A finite eigenvalue in the thermodynamic limit indicates the condensation of eigen microstate and the emergence of phase, similar to and being a generation of the Bose–Einstein condensation of Bose gas. Under the renormalization of a factor b, the largest renormalized eigenvalue 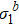 has two trivial fixed points at low and high temperature limits respectively and the critical fixed point with the RG relation
has two trivial fixed points at low and high temperature limits respectively and the critical fixed point with the RG relation 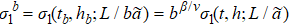 , where β and ν are the critical exponents of order parameter and correlation length, respectively. With the d-dimensional Ising models, it has been demonstrated that the RG theory of eigen microstates can be used to identify the critical point and to predict critical exponents and universality class. Our theory is able to deal with both equilibrium and non-equilibrium systems without caring for the Hamiltonian, which is the foundation of Wilson's RG theory and, however, is absent for most complex systems.
, where β and ν are the critical exponents of order parameter and correlation length, respectively. With the d-dimensional Ising models, it has been demonstrated that the RG theory of eigen microstates can be used to identify the critical point and to predict critical exponents and universality class. Our theory is able to deal with both equilibrium and non-equilibrium systems without caring for the Hamiltonian, which is the foundation of Wilson's RG theory and, however, is absent for most complex systems.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 12135003). We thank Professor Hui Li and Professor Zengru Di for helpful discussions.







