Abstract
Fine-structure line emission from [Ne ii] is observed in the infrared (12.81 μm) and could serve as a diagnostic of X-ray irradiation in protoplanetary disks. [Ne ii] emission may also trace the disk gas and indicate the presence of shocks due to outflows. As the electron fraction decreases with decreasing height from the plane of a disk, collisions with atomic hydrogen begin to play an important role in populating excited fine-structure levels. We present computations of cross sections for fine-structure excitation in collisions of  with atomic hydrogen using a fully quantal molecular-orbital close-coupling approach with complete angular momentum coupling. The results are based on accurate calculations of NeH+ molecular potentials obtained from the multireference single- and double-excitation configuration interaction method. We find that the excitation cross sections are dominated by resonances at energies below 1000 cm−1. Quenching rate coefficients are given at temperatures (10–2000 K) of astronomical interest and compared with the electron impact rate.
with atomic hydrogen using a fully quantal molecular-orbital close-coupling approach with complete angular momentum coupling. The results are based on accurate calculations of NeH+ molecular potentials obtained from the multireference single- and double-excitation configuration interaction method. We find that the excitation cross sections are dominated by resonances at energies below 1000 cm−1. Quenching rate coefficients are given at temperatures (10–2000 K) of astronomical interest and compared with the electron impact rate.
Export citation and abstract BibTeX RIS
1. Introduction
Fine-structure excitation of low-charged ions is an important cooling mechanism in most interstellar environments. The [Ne ii] (12.8 μm) emission line is believed to be useful for determining the elemental neon abundance in planetary nebulae and may contribute significantly to the characteristic cosmological infrared background radiation (Bahcall & Wolf 1968). Because neutral neon has an ionization energy for the K-shell of ∼900 eV, the abundance of ionized neon is expected to be sensitive to the X-ray radiation. Previous work (Glassgold et al. 2007; Meijerink et al. 2008; Güdel et al. 2010; Schisano et al. 2010; Shang et al. 2010; Aresu et al. 2012) proposed that the [Ne ii] fine-structure line could serve as a diagnostic or tracer of far-ultraviolet and X-ray irradiated protoplanetary disks. The [Ne ii] emission could also be a tracer of shocks produced by the interaction between a protostellar outflow and the interstellar medium (Hollenbach & McKee 1989; Hollenbach & Gorti 2009). The [Ne ii] 12.81 μm line has been observed in numerous protoplanetary disks (PPDs) with Spitzer (Espaillat et al. 2007; Sacco et al. 2012) and the Very Large Telescope (VLT) (Baldovin-Saavedra et al. 2012), for example. It has also been observed in the dwarf starburst galaxy He 2–10 with TEXES on the NASA Infrared Telescope Facility (Beck et al. 2015).
Once the neon ions are produced by X-rays, they can subsequently be collisionally excited. Hydrogen-atom collisions are more important than electron collisions when the electron concentration is less than or of the order of 10−2 of the hydrogen concentration; for a collisional ionized plasma this implies a temperature of ≲104 K (Bahcall & Wolf 1968). However, no calculations for fine-structure transitions of Ne+ induced by hydrogen atoms have been reported. Using the approach of Bahcall & Wolf (1968), Hollenbach & McKee (1989) estimated the rate coefficient for the Ne ii de-excitation of the 12.8 μm transition in collisions with atomic hydrogen to be 1.3 × 10−9 cm3 s−1. However, Meijerink et al. (2008) compared the quantum calculations of Barinovs et al. (2005) for C+ + H collisions with the Bahcall–Wolf approximation and found the latter might overestimate the rate coefficients. Meijerink et al. (2008) suggested a reduction factor of ∼6.5, which gives the rate coefficient for collisional deexcitation of the Ne ii fine-structure doublet of ∼2 × 10−10 cm3 s−1, independent of temperature. Quantum-mechanical calculations for [O i] and [C i] (Abrahamsson et al. 2007) give further evidence that the Bahcall–Wolf theory might predict the wrong temperature dependence for the collisional excitation rate coefficient due to atomic hydrogen.
There has been considerable theoretical interest in the collision problem involving one P-state ion or atom with an S-state collision partner (Mies 1973; Launay & Roueff 1977; Chambaud et al. 1980; Zygelman et al. 1992; Krems & Buchachenko 2000; Zhao et al. 2005), while Krems et al. (2004) reported a general expansion for the interaction potential between two atoms in arbitrary angular momentum states. Adopting the method of Krems et al. (2004), we perform the first close-coupling calculations for the fine-structure excitation of Ne+ by atomic hydrogen. In Section 2, we discuss the NeH+ potential energies adopted for the scattering calculations, which are described in Section 3. Section 4 presents the computed cross sections and rate coefficients with comparison to earlier estimates.
2. Interatomic Potential
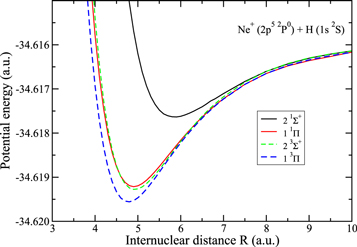
The adiabatic potential energy curves used in the present work are obtained with the ab initio multireference single- and double-excitation configuration interaction (MRD-CI) method with configuration selection and energy extrapolation. For the neon atom, the (15s, 10p, 2d) basis employed was contracted to [9s, 6p, 2d] (Kendall et al. 1992), while the (8s, 2p) basis for hydrogen was contracted to [5s, 2p] and augmented by one s-, one p-, and one d-type diffuse function with exponents of 0.0195, 0.042, and 0.011, respectively. Figure 1 presents the resulting potentials for NeH+ adopted for the scattering calculations. The MRD-CI method has been adequately reported in the work of Buenker & Peyerimhoff (1974), Krebs & Buenker (1995), and Buenker et al. (2016). The same MRD-CI package has been applied previously to treat the [OHe]3+ (Wu et al. 2009b) and [CHe]3+ (Wu et al. 2009a) systems. The results were compared with asymptotic atomic experimental data with errors in the calculated energies small enough to be adequate for scattering calculations. Table 1 lists a summary of experimental and theoretical values of the well depth (De) and equilibrium internuclear distances (re) for the ground and excited electronic states. The only available experimental well depth is derived from electron spectra due to associative ionization for the ground state potential (Hotop et al. 1998). Gerivani et al. (2015) presented calculations of the ground and excited electronic potentials with calculations carried out at the MRCI-DKH (Douglas–Kroll–Hess; Douglas & Kroll 1974; Hess 1985, 1986) level of theory, whereas the ground state from Pendergast et al. (1994) used CCSD(T) calculations. The MRD-CI program and basis sets have been improved compared to those used for the ground state calculations from Petsalakis et al. (1998), in which the focus was the on ground and Rydberg states of NeH.
Figure 1. Electronic potentials for NeH+ adopted for the current scattering calculations.
Download figure:
Standard image High-resolution imageTable 1. Spectroscopic Constants for the Electronic Potentials of NeH+
| State | De (eV) | re (a0) | |
|---|---|---|---|
X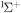
|
2.275(25) | 1.8731 | Exp.a |
| 2.287 | 1.876 | Cal.b | |
| 2.29 | 1.895 | Cal.c | |
| 2.30(2) | 1.874 | Cal.d | |
| 2.43 | 1.867 | This work | |
b
|
0.07451 | 5.013 | Cal.b |
| 0.06761 | 5.061 | Cal.d | |
| 0.10110 | 4.783 | This work | |
a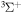
|
0.06199 | 5.104 | Cal.b |
| 0.07903 | 4.985 | Cal.d | |
| 0.09360 | 4.922 | This work | |
B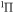
|
0.05641 | 5.240 | Cal.b |
| 0.09155 | 4.902 | This work | |
A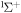
|
0.03794 | 5.980 | Cal.b |
| 0.04886 | 5.870 | This work | |
Notes.
aExperimental values from Hotop et al. (1998). bCalculated values from Gerivani et al. (2015). cCalculated values from Petsalakis et al. (1998). dCalculated values from Pendergast et al. (1994).Download table as: ASCIITypeset image
There are four molecular electronic states arising from Ne+(2P) + H(2S) interaction, namely  ,
,  ,
,  , and
, and  . Although Ne(1S) + H+(1S) correlates to the ground state of NeH+, its energy gap is over 10 eV, which is much larger than the fine-structure splitting of Ne+(2P) (0.097 eV). Therefore, four Ne+(2P) + H(2S) channels, 2 (or A)
. Although Ne(1S) + H+(1S) correlates to the ground state of NeH+, its energy gap is over 10 eV, which is much larger than the fine-structure splitting of Ne+(2P) (0.097 eV). Therefore, four Ne+(2P) + H(2S) channels, 2 (or A)  , 1 (or B)
, 1 (or B)  , 2 (or a)
, 2 (or a)  , and 1 (or b)
, and 1 (or b)  , are included in our fully quantal molecular-orbital close-coupling approach. These states separate into two manifolds corresponding to
, are included in our fully quantal molecular-orbital close-coupling approach. These states separate into two manifolds corresponding to  and
and  terms split by the spin–orbit interaction.
terms split by the spin–orbit interaction.
We used the ab initio potentials up to R = 20.0 a0. Within the data range, we interpolate to a step size 0.001 a0, applying a cubic spline method. Three points were added between R = 10.0 a0 and 20.0 a0 using the fitting function  to improve the spline interpolation smoothness. Beyond the ab initio data, for smaller interatomic distances, the potential is fit to
to improve the spline interpolation smoothness. Beyond the ab initio data, for smaller interatomic distances, the potential is fit to  , while the leading term in the long range part of an ion–neutral potential is the charge-induced-dipole interaction
, while the leading term in the long range part of an ion–neutral potential is the charge-induced-dipole interaction  with the static dipole polarizability for hydrogen αH = 4.5 au, resulting in a strong attraction at large separation.
with the static dipole polarizability for hydrogen αH = 4.5 au, resulting in a strong attraction at large separation.
3. Collisional Treatment
The method of our scattering calculations is based on the work of Mies (1973), Zygelman et al. (1992), and Krems et al. (2004). The Hamiltonian of the Ne+ + H collision system can be written (in atomic units) in the form
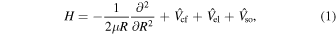
where R is the interatomic distance, μ is the reduced mass,  is the centrifugal interaction,
is the centrifugal interaction,  is the electrostatic interaction, and
is the electrostatic interaction, and  denotes the spin–orbit interaction.
denotes the spin–orbit interaction.
The total wave function is expanded in the scattering basis  , where j = jA + jB is the total electronic angular momentum of the diatomic system and J = j + l is the total angular momentum of the system. The reduced radial Schrödinger equation describing the internal states of the NeH+ molecule can be written as
, where j = jA + jB is the total electronic angular momentum of the diatomic system and J = j + l is the total angular momentum of the system. The reduced radial Schrödinger equation describing the internal states of the NeH+ molecule can be written as
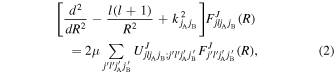
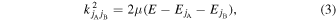
where E is the total energy and  is the reduced radial wave function with A referring to Ne+ and B referring to H. In the basis
is the reduced radial wave function with A referring to Ne+ and B referring to H. In the basis  , the spin–orbit coupling matrix is diagonal and the nonzero elements are the fine-structure splitting energies (
, the spin–orbit coupling matrix is diagonal and the nonzero elements are the fine-structure splitting energies ( ,
,  ). We adopt
). We adopt  and
and  cm−1 (Kramida et al. 2018). The elements of the electrostatic interaction matrix
cm−1 (Kramida et al. 2018). The elements of the electrostatic interaction matrix  are expressed in terms of the Born–Oppenheimer potentials
are expressed in terms of the Born–Oppenheimer potentials  . The complete formalism is described in Krems et al. (2004) and Barinovs et al. (2005).
. The complete formalism is described in Krems et al. (2004) and Barinovs et al. (2005).
The radial coupled equations are solved with the log-derivative method of Johnson (1973). The scattering matrix can be obtained from the numerical results of the log-derivative calculation and asymptotic radial wave functions. Cross sections are then calculated using the relation (Chambaud et al. 1980):
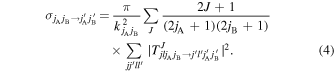
The T matrix is related to the scattering matrix S by T = I − S. A sufficient number of partial waves J (the maximum number of partial waves was 300) are used and tested to ensure convergence for each fixed collision energy E.
4. Results and Discussion
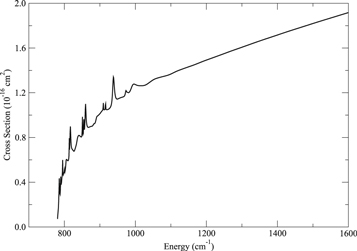
The cross sections for fine-structure excitation of Ne+( ) is presented in Figure 2. At energies near threshold the cross section is dominated by orbiting resonances. Above 1000 cm−1, the cross section increases linearly with collision energy. Figure 3 presents the cross sections for fine-structure deexcitation of Ne+(
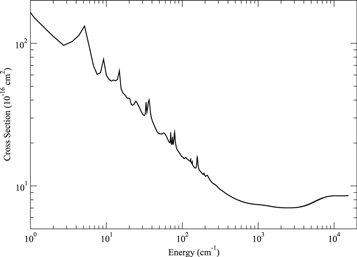
) is presented in Figure 2. At energies near threshold the cross section is dominated by orbiting resonances. Above 1000 cm−1, the cross section increases linearly with collision energy. Figure 3 presents the cross sections for fine-structure deexcitation of Ne+( ). Many resonances are observed in the low-energy region, while the cross section tends to be smooth at energies above 200 cm−1.
). Many resonances are observed in the low-energy region, while the cross section tends to be smooth at energies above 200 cm−1.
Figure 2. Excitation cross sections for Ne+( ) + H(
) + H( ) → Ne+(
) → Ne+( ) + H(
) + H( ) as a function of the center-of-mass kinetic energy.
) as a function of the center-of-mass kinetic energy.
Download figure:
Standard image High-resolution imageFigure 3. Deexcitation cross sections for Ne+( ) + H(
) + H( ) → Ne+(
) → Ne+( ) + H(
) + H( ) as a function of the center-of-mass kinetic energy.
) as a function of the center-of-mass kinetic energy.
Download figure:
Standard image High-resolution imageThe quenching rate coefficients were obtained by thermally averaging the deexcitation cross sections over a Boltzmann distribution of collision energies,
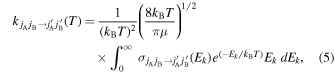
where Ek is the kinetic energy, and kB is Boltzmann's constant.
Wang et al. (2017) calculated the effective collision strength ( ) for the electron-impact fine-structure excitation of Ne+. As a comparison to our hydrogen-induced quenching rate, we obtained the electron-impact quenching rate coefficient qfi (in units of cm3 s−1) by
) for the electron-impact fine-structure excitation of Ne+. As a comparison to our hydrogen-induced quenching rate, we obtained the electron-impact quenching rate coefficient qfi (in units of cm3 s−1) by
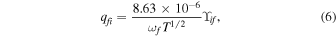
where  is the statistical weight of the final (upper) state. Using detailed balance, we could further obtain the excitation rate coefficient
is the statistical weight of the final (upper) state. Using detailed balance, we could further obtain the excitation rate coefficient 
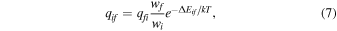
where ωi is the statistical weight of the initial (lower) state, and ΔEif is the energy gap. The cooling efficiency can be calculated from the excitation rates very easily, which is often used in astrophysical and plasma applications.
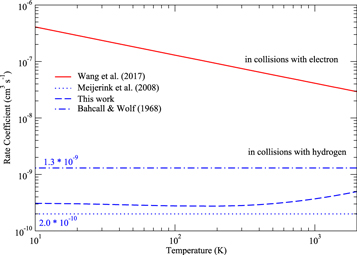
In Figure 4 we compare the quenching rate coefficients for Ne+( ) → Ne+(
) → Ne+( ) in collisions with electrons and atomic hydrogen. Generally, the deexcitation rate of Ne+(
) in collisions with electrons and atomic hydrogen. Generally, the deexcitation rate of Ne+( ) due to collisions with electrons is much larger than with hydrogen. At 10 K, the magnitude of qe is higher than kH by a factor of 1000, while at 2000 K, this factor drops to about 100. Compared to the temperature-independent estimates, our results are closer to the adjusted estimates of Meijerink et al. (2008), while the Bahcall & Wolf (1968) approximation overestimates the rate coefficients by a factor of ∼4. We tabulated part of our results in Table 2 and the full data set is available online.5
) due to collisions with electrons is much larger than with hydrogen. At 10 K, the magnitude of qe is higher than kH by a factor of 1000, while at 2000 K, this factor drops to about 100. Compared to the temperature-independent estimates, our results are closer to the adjusted estimates of Meijerink et al. (2008), while the Bahcall & Wolf (1968) approximation overestimates the rate coefficients by a factor of ∼4. We tabulated part of our results in Table 2 and the full data set is available online.5
Figure 4. Quenching rate coefficients for electron-impact (Wang et al. 2017) and hydrogen-induced (this work) fine-structure transition Ne+( ) + H(
) + H( ) → Ne+(
) → Ne+( ) + H(
) + H( ) as functions of the temperature. Estimates for Ne+ + H collision rates by Bahcall & Wolf (1968) and adjusted rates (Meijerink et al. 2008) are also plotted.
) as functions of the temperature. Estimates for Ne+ + H collision rates by Bahcall & Wolf (1968) and adjusted rates (Meijerink et al. 2008) are also plotted.
Download figure:
Standard image High-resolution imageTable 2. The Quenching Rate Coefficientsa
| T | kHb | qec |
|---|---|---|
| (K) | (10−10 cm3 s−1) | (10−10 cm3 s−1) |
| 10 | 3.08 | 4.09 × 103 |
| 40 | 2.91 | 2.04 × 103 |
| 70 | 2.82 | 1.55 × 103 |
| 100 | 2.77 | 1.29 × 103 |
| 300 | 2.81 | 7.50 × 102 |
| 600 | 3.17 | 5.30 × 102 |
| 900 | 3.56 | 4.34 × 102 |
| 2000 | 4.97 | 2.93 × 102 |
Notes.
aAdditional data are given in the online table. bThis work; fine-structure quenching rate induced by collisions with atomic hydrogen. cFrom Wang et al. (2017); fine-structure quenching rate induced by collisions with electron.Download table as: ASCIITypeset image
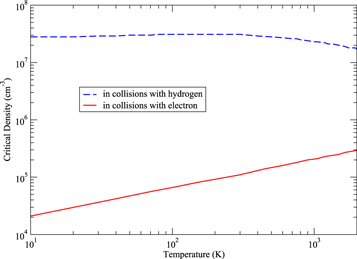
The critical density for the upper level jA =  is
is
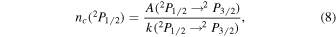
where 
 is the spontaneous transition probability (Kramida et al. 2018). The knowledge of the collisional deexcitation rate coefficient is important if the density of the collision partner is smaller than this value. In Figure 5, we plot the calculated results. First, the new calculated critical density for hydrogen (nHc) is larger than the previously estimated value
is the spontaneous transition probability (Kramida et al. 2018). The knowledge of the collisional deexcitation rate coefficient is important if the density of the collision partner is smaller than this value. In Figure 5, we plot the calculated results. First, the new calculated critical density for hydrogen (nHc) is larger than the previously estimated value  cm−3 (Osterbrock & Ferland 2006). The differences mean that the conditions thought to be in local thermal equilibrium (LTE) should now be investigated with a non-LTE analysis. Second, the values of
cm−3 (Osterbrock & Ferland 2006). The differences mean that the conditions thought to be in local thermal equilibrium (LTE) should now be investigated with a non-LTE analysis. Second, the values of  and
and  are 1.7 × 107 and 2.9 × 105 cm−3, respectively, at T = 2000 K. When the ionization fraction (or electron to H abundance ratio) is less than ∼10−2, H collisions will dominant with the Ne+ fine-structure levels following out of equilibrium below ∼107 cm−3.
are 1.7 × 107 and 2.9 × 105 cm−3, respectively, at T = 2000 K. When the ionization fraction (or electron to H abundance ratio) is less than ∼10−2, H collisions will dominant with the Ne+ fine-structure levels following out of equilibrium below ∼107 cm−3.
Figure 5. Critical densities for collisional deexcitation of Ne+( ) → Ne+(
) → Ne+( ) due to atomic hydrogen or electron collisions as functions of temperature.
) due to atomic hydrogen or electron collisions as functions of temperature.
Download figure:
Standard image High-resolution image5. Summary
Using the new calculated NeH+ potentials, we present rate coefficients for fine-structure deexcitation in collisions of Ne+(2P) with atomic hydrogen at temperatures ranging from 10 to 2000 K. Our results show that the Bahcall–Wolf approximation overestimates the rate coefficients by a factor of ∼4, on average. Calculations based on this approximation may underestimate the [Ne ii] μm flux. Given the recent progress in interstellar spectroscopy, the calculations presented here should improve our understanding of the conditions of X-ray-irradiated protoplanetary disks.
We thank Prof. Al Glassgold and Prof. Nick Abel for pointing out the importance of this process. We are sorry to learn that Prof. Glassgold has recently passed away. This work was supported by NASA grant NNX1SAE47G. Computing resources were provided by the Georgia Advanced Computing Resource Center and Center for Simulational Physics at the University of Georgia.
Footnotes
- 5
Rate coefficient data in the Leiden Atomic and Molecular Database (LAMDA, Schöier et al. 2005) format can be obtained at www.physast.uga.edu/amdbs/excitation/.