Abstract
The confirmation and constraints of a Europa-generated neutral torus are presented based on available observations and computational modeling of relevant source species. These results are applied to determine if the Energetic Neutral Atom (ENA) images reported by Mauk et al. were produced by interactions with a Europa neutral particle torus or with the local charged particle population. Neutral tori provide important insights into the processes operating in large planet magnetospheres. Such features emerge when particles escape an embedded satellite and form a population that co-orbits with the moon. Torus distributions and compositions are directly related to the satellite composition and source mechanisms. Significant findings are as follows. (1) The presence of a Europa neutral torus is confirmed through the development of 3D Io and Europa neutral tori models. (2) Density constraints for H, H2, O, and O2 in the Europa neutral torus are determined. (3) The torus is highly asymmetric: Near Europa, ∼99% of the ENA image is produced by the neutral torus. Furthest from Europa, ∼15%–69% of the ENA emissions are caused by charge exchange interaction within the ambient plasma. In addition, we showed that (4) 7%–34% of the ENAs near Europa would be produced by charge exchange with neutrals, even with a three order of magnitude neutral source rate reduction (<2 × 1024). (5) Satellite source rate variations take longer to impact the Europa neutral torus than the Io neutral torus. Dominant processes at Europa's orbit have lifetimes >2–8 days, while at Io, the neutral particles lifetimes are as short as 8–13 hr.
Export citation and abstract BibTeX RIS
1. Introduction
The purpose of this paper is to confirm the presence of a Europa neutral torus, particularly with respect to the Mauk et al. (2003) observations which actually may have been detecting a local plasma population. Neutral tori form when atoms and molecules escape from a moon and establish a population that co-orbits with it. If these particles survive long enough, they can form a partial or full ring of particles along the moon's orbit, which is referred to as a torus. Tori distributions and compositions are a direct result of satellite composition and source mechanisms (including source variability). Understanding a neutral torus, then, can often provide critical insight into a source that might not be directly observable. Additionally, tori interact and respond to magnetospheric processes so the distribution and composition of these features can often provide significant, if not unique, insight into the processes, dynamics, and mechanisms of large planet magnetospheres.
Studies of neutral tori are particularly important for understanding the plasma ionization rates in Jupiter's magnetosphere and the surface composition of the moons contained within it. The Jovian system is intriguing in that it contains extremely different particle sources ranging from the volcanic moon, Io (which populates the system with sulfur dioxide products as well as other minor species), to the frozen world of Europa (which is thought to eject oxygen, hydrogen, and water products), both of which exist inside Jupiter's intense radiation environment. While multiple spacecraft have provided historic observations of this intriguing environment, they have also raised numerous questions. Characterizing Io (i.e., volcanic versus sublimation) as well as Europa particle sources (including the possibility of plumes and subsurface ocean) has become such a priority that NASA and ESA are planning multiple missions to this system.
The primary source of material in the Jovian magnetosphere is Io, the volcanic moon that emits between 700 and 2400 kg of sulfur and oxygen per second (Smyth & Marconi 2003; Dols et al. 2008). The emitted neutral particles begin the process of forming a torus, but the Jovian magnetospheric electrons ionize these particles relatively quickly (Delamere et al. 2007). These newly charged particles then form a plasma torus, with these particles eventually transported throughout the magnetosphere under the influence of Jupiter's fast rotating and intense magnetic field. Also of interest is the icy moon Europa, which orbits further from Jupiter but less than 4 Jupiter Radii (RJ, 71,492 km) from Io's orbit. Europa is reported to have a subsurface liquid water ocean (Carr et al. 1998), making it the target of future missions to study its habitability. Europa's potential habitability has become an even greater topic of interest with the discovery of activity suggested to be plumes emanating from its surface (Intriligator & Miller 1982; Roth et al. 2014; Sparks et al. 2017, and Jia et al. 2018). While instruments can observe the surface composition of Europa, our ability to assess its habitability—or even search for possible signs or precursors of life—is limited because it is currently not possible to directly observe the subsurface ocean. That being said, material originating below Europa's surface (reaching the surface by geologic activity and eventually ejected) can reveal important insights (e.g., Johnson & Sundqvist 2018) and could be detectable as components of a neutral torus. Unfortunately, the source rate from Europa is estimated to be two orders of magnitude lower than Io (Smyth & Marconi 2006). This makes direct detection challenging by comparison to Io's much larger source (Steffl et al. 2004; Yoshioka et al. 2013).
The first suggestion of a Europa plasma torus was by Intriligator and Miller (1982), based on plasma observations from Pioneer 11 and Voyagers 1 and 2, with the first indications of a Europa-generated neutral torus reported by Lagg et al. (2003). They observed a depletion of 80–220 keV protons (around 90° pitch angles) but no depletion at energies above 220 keV along Europa's orbit. From these observations, Lagg et al. (2003) proposed that the presence of neutrals in the vicinity of Europa's orbit was depleting these equatorial bound protons through charge exchange interactions. These observations illustrated that while direct detection of a Europa neutral torus is extremely challenging, indirect detection might be achieved as a result of charge exchange interactions. Unfortunately, the lack of equatorial bound protons is not conclusive evidence for a Europa-generated neutral torus because other processes could also produce the observed feature.
Fortunately, it is possible to indirectly detect a Europa torus making use of Energetic Neutral Atom (ENA) imaging. This innovative technique detects energetic neutrals that are produced as a result of charge exchange interactions. ENAs can be produced by interactions between a neutral particle and an ion. In simplistic terms, the neutral particle loses an electron and the charged particle gains an electron, effectively "exchanging" their charges. When the magnetic field is rotating faster than the orbital velocity, as is the case at Europa's orbit (∼110.7 km s−1 versus ∼13.7 km s−1), the neutral particle becomes a fresh ion that is picked up by and then rotates along with the planetary magnetic field. The neutralized ion, though, is no longer bound by the magnetic field but typically moves too fast to remain bound by the gravitational field at that orbital location, becoming an energetic neutral. A fraction of the ENAs originating from Europa's orbit move fast enough to ballistically escape from the Jovian system. If the change in the gravitational field between the source and detector is small compared to the particle's energy, these neutrals move along trajectories that originate from the original source particle location approximately along a straight line. Such particles detected at a distance from the source will have a spatial distribution essentially producing an "image" of the original source population by tracking the emissions along a line of sight back to their origin. Such ENAs have been used to produce images of the ring current of the Earth (Roelof 1987).
Mauk et al. (2003) reported the detection of a Europa neutral torus using hydrogen ENA observations. They observed these ENAs with the Ion and Neutral Camera (INCA) on the Cassini Magnetosphere Imaging Instrument (Krimigis et al. 2004) during the Cassini fly-by of Jupiter (late 2000 and early 2001) in the range of 50–80 keV over an integration time of approximately 15 hr. They suggested that these fast-moving hydrogen atoms were a result of protons charge exchanging with a neutral gas torus in the region of Europa's orbit. Mauk et al. (2004) combined these observations with integral ion moments and composition, as well as modeling, to place initial constraints on a Europa neutral torus.
Unlike in Saturn's magnetosphere, where neutral particles dominate, Jupiter's magnetosphere is dominated by charged particles (Delamere et al. 2007). Therefore, in this dense plasma environment, ENAs can also be produced as a result of charge exchange interactions between two ionized particles. Such ENAs cannot be used to infer the presence of neutral torus, so the possibility of charged particles interacting with other charged particles must be considered before interpreting the ENA observations.
Therefore, the significant population of charged particles in Jupiter's magnetosphere could alter the interpretation of ENA observations, which raises the question of whether Mauk et al. (2003) observed a Europa-generated neutral particle torus or simply an interaction of protons with ions in the plasma torus that may or may not have originated from Europa. A detailed examination of all possible source interactions is needed to ascertain the likely source population. In this paper, we wish to determine whether or not the Mauk et al. (2003) observations were actually generated by a neutral torus emanating from Europa. We first identify the possible major sources that could produce ENAs and then determine their relative likelihood of accounting for the observations. We also produce updated models for the Io and Europa-generated neutral tori for primary source species. In this paper, we do not consider the potential Europa plume source, as the limited observations indicate this to be a highly variable and short-lived phenomenon. The possible perturbations from such a localized source will be a topic for our future research. The results obtained are used to construct a Europa neutral torus model and place constraints on the torus. They can also help determine the likelihood that ENAs in other planetary or exo-planetary systems can be produced by interaction with neutral source particles.
2. Neutral Torus Particle Interaction Rates
The first step of this research is to calculate ion interaction rates with potential Europa torus neutrals. These rates will be used to determine whether or not the Mauk et al. (2003) observations were produced by a Europa neutral torus or simply the ambient plasma population that could originate from Io. Mauk et al. measured H ENAs presumably as a result of charge exchange of an H+ with a neutral or charged torus particle. Since Mauk et al. (2003) assumed that these protons interacted with Europa neutrals, we first consider such interactions. The primary species escaping from Europa that could form a neutral torus are H, H2, O, and O2 (Smyth & Marconi 2006), so the possible charge exchange interactions that could produce the observed ENAs are
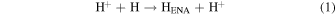
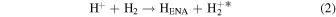
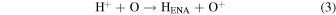
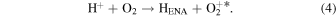
For proton charge exchange with H2 and O2, an ENA can be produced that results in several different sets of dissociation products. Here we are only concerned with the ENA product, so we have combined the separate reaction products (annotated with an asterisk). The interaction rates (or the reciprocal of particle interaction lifetimes) for the provided processes determine the likelihood that a proton will interact with a population of specific neutrals. Mauk et al. (2003) observed 50–80 keV ENAs. Assuming the charge exchange for the fast protons involves little scattering, the incident H+ had energies of ∼50–80 keV. Thus, we only calculate charge exchange interaction rates, α(r)n, for this energy range using
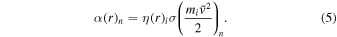
Here n labels the specific charge exchange process, i is the local target species, η(r)i is the local neutral density, mi is the ion mass,  is the average collision speed (the difference in velocity between the incident ion and the target neutral particle), and σ(miv2/2)n is the energy-dependent charge exchange cross section. Several references exist for the provided interaction cross sections from 50 to 80 keV, including Stier & Barnett (1956), McClure (1966), Rudd et al. (1983), Rudd et al. (1985), Tawara et al. (1985), Basu et al. (1987), Rees (1989), Shah et al. (2009), Luna et al. (2005), and Lindsay and Stebbings (2005). With the exception of Rudd et al. (1985), all of these cross sections are relatively consistent. We thus omitted the results from Rudd et al. (1985) and averaged all the other results to produce the required charge exchange cross sections (for incident ions onto neutral particles) in Table 1.
is the average collision speed (the difference in velocity between the incident ion and the target neutral particle), and σ(miv2/2)n is the energy-dependent charge exchange cross section. Several references exist for the provided interaction cross sections from 50 to 80 keV, including Stier & Barnett (1956), McClure (1966), Rudd et al. (1983), Rudd et al. (1985), Tawara et al. (1985), Basu et al. (1987), Rees (1989), Shah et al. (2009), Luna et al. (2005), and Lindsay and Stebbings (2005). With the exception of Rudd et al. (1985), all of these cross sections are relatively consistent. We thus omitted the results from Rudd et al. (1985) and averaged all the other results to produce the required charge exchange cross sections (for incident ions onto neutral particles) in Table 1.
Table 1. Averaged Neutral-ion Charge Exchange Cross Sections (cm2) for 50–89 keV Incident Protons on H, H2, O, and O2 Averaged from Stier & Barnett (1956), McClure (1966), Rudd et al. (1983), Tawara et al. (1985), Basu et al. (1987), Rees (1989), Shah et al. (2009), Luna et al. (2005), and Lindsay and Stebbings (2005)
| Average cross sections (cm2) | ||||||||
|---|---|---|---|---|---|---|---|---|
| keV | H+ + H → H + H+ |
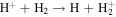
|
H+ + O → H + O+ |
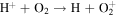
|
||||
| 50 | 1.0E-16 | +/−15.0% | 1.9E-16 | +/−4.9% | 2.0E-16 | +/−29.8% | 3.1E-16 | +/−19.0% |
| 60 | 6.4E-17 | +/−7.7% | 1.2E-16 | +/−1.5% | 1.7E-16 | +/−24.5% | 2.5E-16 | +/−17.5% |
| 70 | 3.8E-17 | +/−15.5% | 8.4E-17 | +/−6.2% | 1.5E-16 | +/−30.0% | 2.0E-16 | +/−16.3% |
| 80 | 2.5E-17 | +/−6.3% | 6.0E-17 | +/−13.9% | 1.3E-16 | +/−27.9% | 1.7E-16 | +/−17.0% |
Note. Median values with standard deviation percentages are shown.
Download table as: ASCIITypeset image
Equation (5) also depends on the target neutral population density. Mauk et al. (2003) and Lagg et al. (2003) derived Europa torus average densities of ∼40 and ∼20–25 particles cm−3, respectively. Smyth and Marconi (2006) used sputter source rates to derive peak average densities of ∼90 H2 cm−3 and ∼4.9 O cm−3 at Europa's orbit. However, there are some poorly constrained variables and assumptions in these results, so we treat the neutral density as a variable. For the purpose of illustration, and for initial comparison to interaction rates between charged particles, we apply the 40 cm−3 neutral density reported by Mauk et al. (2003). These results assume the torus is only composed of each single neutral species. Since the interaction rates scale linearly with neutral particle density, the relative differences in the rates are preserved.
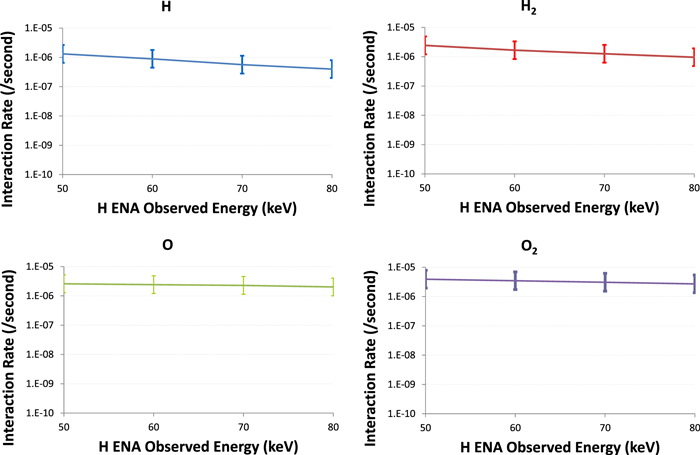
To compute these interaction rates, the relative velocities between the incident proton and target neutrals are needed. We determine the average collision speed as the difference between H+ velocity distribution (that incorporates ion gyro-motion) and the Keplerian orbital speed of the neutrals. We use the associated plasma velocities near Europa's orbit from Bagenal et al. (2015), reported as 123, 98, and 76 km s−1 for the 10th percentile, median, and 90th percentile cases, respectively, along with the Keplerian speed (∼13.7 km s−1) to compute  for Equation (5). We can now calculate the interaction rates for charge exchange of 50–80 keV H+ with potential Europa tori composed of H, H2, O, and/or O2. The resulting interaction rates are shown in Figure 1. The range of H+ velocities with the impact of reducing and increasing neutral densities by a factor of two is represented by the error bars to illustrate the sensitivity to this parameter.
for Equation (5). We can now calculate the interaction rates for charge exchange of 50–80 keV H+ with potential Europa tori composed of H, H2, O, and/or O2. The resulting interaction rates are shown in Figure 1. The range of H+ velocities with the impact of reducing and increasing neutral densities by a factor of two is represented by the error bars to illustrate the sensitivity to this parameter.
Figure 1. Neutral-ion charge exchange interaction rates (per second) for producing an observed hydrogen energetic neutral atom as a function of its energy and target species at a nominal density of 40 cm−3. Error bars are a convolution of the plasma environment variation and reduction/increase in neutral densities by a factor of two (i.e., 80 and 20 cm−3—interaction rates scale linearly with neutral density). The interaction rate axis scale is selected for consistency and comparison to the following plasma torus interaction rates.
Download figure:
Standard image High-resolution image3. Plasma Torus Particle Interaction Rates
We now examine the contribution to the Mauk et al. (2003) observations from H+ capturing an electron from other torus ions. Similar to Section 2, we consider only incident 50–80 keV protons, but in this case we need to consider target plasma torus populations. Unlike the neutral particle population at Europa's orbit, the plasma population includes charged particles that originate from Io (Bagenal 1994). Based on Bagenal et al. (2015), the primary target ions of interest for charge exchange with source protons are S+, S++, S+++, O+, and O++:

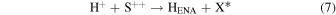
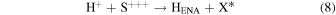
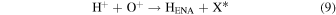
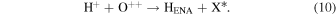
Again, the resulting ion product is not relevant, so pathways are combined and annotated as X*. Similar to the process noted previously, we first determine the cross sections. Unfortunately, limited experimental data exists for charge exchange between ions in this energy range. The primary reference for these interactions is Fujiwara (1976), which applies a Coulomb–Born approximation to determine the total charge transfer cross sections between protons and highly ionized atoms. Coulomb–Born approximations are applicable at energies above the Bohr velocity (the velocity of an electron in the first orbit), which for H+ is
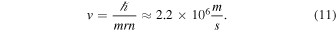
Here ℏ is the reduced Planck's constant, r is the Bohr radius, n is 1, and m is the electron mass. The Bohr velocity for a proton is ∼25.1 keV. Since we are concerned with incident H+ at 50–80 keV, this approximation is acceptable. Fujiwara (1976) provides the necessary cross sections for charge exchange with oxygen ions (O+ and O++) but does not examine sulfur ions. We approximate the sulfur ion cross sections by selecting other ions with similar ionization energies. In particular, as an approximation for charge exchange with S+ (2nd ionization energy of ∼23.33 eV), we apply calculations for C+ that have similar 2nd ionization energies of ∼24.39 eV. Next, we use charge exchange with O+ (2nd ionization energy of ∼35.11 eV) to approximate charge exchange with S++ (3rd ionization energy of ∼34.78 eV). Finally, we use charge exchange with C++ (3rd ionization energy of ∼47.89 eV) to approximate charge exchange with S+++ (4th ionization energy of ∼47.22 eV). These assumptions result in the cross sections shown in Table 2.
Table 2. Derived Ion–Ion Charge Exchange Cross Sections (cm2) for 50–89 keV Incident Protons on O+, O++, S+ (Approximated with C+), S++ (Approximated with O+), and S+++ (Approximated with C++) from Fujiwara (1976)
| Average cross sections (cm2) | |||||
|---|---|---|---|---|---|
| keV | H+ + O+ | H+ + O++ | H+ + S+(C+) | H+ + S++(O+) | H+ + S+++(C++) |
| 50 | 1.5E-17 | 7.0E-19 | 1.9E-17 | 1.5E-17 | 8.0E-19 |
| 60 | 1.2E-17 | 8.0E-19 | 1.5E-17 | 1.2E-17 | 8.3E-19 |
| 70 | 9.0E-18 | 9.0E-19 | 1.0E-17 | 9.0E-18 | 8.6E-19 |
| 80 | 6.0E-18 | 1.0E-18 | 4.0E-18 | 6.0E-18 | 9.0E-19 |
Download table as: ASCIITypeset image
Measurements of the various ion densities near Europa's orbit are variable and somewhat limited. Steffl et al. (2004) derived relative ion abundances (as compared to electron densities) from Cassini UVIS observations of a region relatively close to Europa's orbit (∼8.8 Rj from Jupiter). Bagenal et al. (2015) also derived multiple plasma parameters for Europa's orbit (based on available Voyager and Galileo observations) on average, as well as low and high plasma densities representing the median, 10th percentile, and 90th percentile plasma environments in order to capture plasma variability. Of particular interest are plasma densities and temperatures. Therefore, we apply the relative ion abundances of Steffl et al. (2004) (convolved with the more recent Yoshioka et al. 2017 observations) to the results of Bagenal et al. (2015) to determine the individual ion densities and temperatures of each of the three plasma conditions. Table 3 shows the resulting ion densities and temperatures we use for determining charge exchange interaction rates. Additionally, similar to the neutral particle charge exchange calculations provided, we apply the plasma velocities from Bagenal et al. (2015) for the 10%, median, and 90% cases.
Table 3. Plasma Densities (cm−3) and Temperatures (eV) Near Europa's Orbit for Low, Average, and High Plasma Conditions (Derived from Steffl et al. 2004, Bagenal et al. 2015, and Yoshioka et al. 2017)
| Density (cm−3) | Temperature (eV) | |||||
|---|---|---|---|---|---|---|
| low | average | high | low | average | high | |
| S+ | 1.7 | 4.3 | 7.9 | 500 | 130 | 70 |
| S++ | 6.1 | 15.2 | 27.9 | 250 | 65 | 40 |
| S+++ | 2.9 | 7.2 | 13.2 | 170 | 45 | 25 |
| O+ | 15.4 | 38.7 | 71.0 | 500 | 130 | 70 |
| O++ | 10.8 | 27.2 | 49.9 | 340 | 90 | 50 |
Download table as: ASCIITypeset image
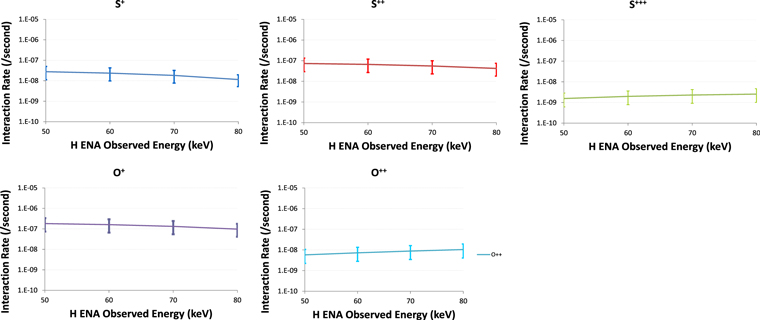
Using the values provided, we calculate the interaction rates for charge exchange of 50–80 keV H+ with S+, S++, S+++, O+ and O++, which could produce the 50–80 keV H ENAs observed by Mauk et al. (2003). For each interaction process at each INCA energy step (i.e., 50, 60, 70 and 80 keV), we apply the associated energy dependent cross section, ion temperature, ion density, and relative velocity between the incident H+ and target to Equation (5) (each ion target population is substituted for the target neutral particle population parameters). Our calculations account for the relative velocity between the incident H+ and the target plasma for the low, average, and high plasma cases shown in Table 3. Our resulting particle interaction rates for a 50–80 keV proton interacting with each particular target ion species are shown in Figure 2. These values represent the likelihood that an observed hydrogen ENA (at each energy) was produced by an interaction with each possible ion species population.
Figure 2. Ion–ion charge exchange interaction rates (per second) for producing an observed hydrogen energetic neutral atom as a function of target ion species (S+, S++, S+++, O+, and O++) and observed energy. Error bars represent high and low bounds based on the range of observed plasma parameters.
Download figure:
Standard image High-resolution imageNotice that these interaction rates are much smaller than the neutral interaction rates noted previously. If any neutral particle species have a density similar to that reported by Mauk et al. (2003), then H ENAs are more likely to be produced by interactions with a Europa neutral torus than interactions with the ambient Io-generated plasma torus. The indicated results provide critical parameters for our neutral torus modeling, which are used to determine what fraction of the Mauk et al. (2003) ENA flux is likely caused by a Europa neutral torus.
4. Europa Source Descriptions
Previously we applied a uniform average 40 cm−3 density across all particle species, which only provides a bound and does not account for asymmetric spatial distributions. In reality, Mauk et al. (2003) observations were produced by interactions with a combination of multiple species with varying spatial distributions. Therefore, we now apply neutral torus modeling to accurately determine how much (if any) of the observed ENAs were produced by a Europa neutral torus.
To model the spatial distribution of the neutral torus, we first define the sources. The dominant magnetospheric source at Jupiter is Io, which orbits at approximately 5.9 planetary radii from Jupiter. Estimates of this volcanic moon's output range from 750 kg s−1 up to 2400 kg s−1 (Saur et al. 2003; Smyth & Marconi 2003; Dols et al. 2008) of neutral SO2. Jupiter differs from Saturn in that at Jupiter, plasma density dominates the neutral density, as this radiation environment causes relatively short neutral lifetimes (Smyth & Marconi 2006). Therefore, the neutral particle populations near Europa's orbit should be dominated by Europa ejecta. The Io-generated neutral particles rapidly ionize or dissociate (followed by ionization) on the order of days, so their density decreases rapidly with radial distance from Io. It is still possible, though, that Io-generated neutrals contributed to the observed ENAs (either neutrals ejected from Io or as a result of ENAs produced from ion charge exchange near Io). Therefore we modeled this source in addition to a Europa source.
While Io is the dominant satellite source at Jupiter, Europa is a source of water-group molecules and decomposition products (H2 and O2), but at a much lower source rate. Smyth and Marconi (2006) estimate atmospheric escape rates of H2 and O, while Dols et al. (2016) report an O2 atmospheric source rate. Molecular oxygen is larger in mass but must number about 50% of H2 particles for stoichiometry. As mentioned earlier, Europa ejects H2O, O2, and H2 (Cassidy et al. 2013). Although Cassidy et al. (2013) report that the surface source rate of H2O is 2 × 1027 s−1 or ∼60 kg s−1, the ejection energies are small, so the H2O tends to return to and freeze on the surface. This is in contrast to the volatiles, O2 and H2, that do not stick at the ambient temperatures of the surface ice. The lighter hydrogen particles can directly populate the torus; however, the heavier molecular oxygen stays closer to the surface until it dissociates (or charge exchanges) and either impacts the surface or escapes into the torus. Therefore hydrogen and oxygen comprise the bulk of the neutral particles escaping from Europa available to form a neutral torus.
Particle source rates are critical parameters for our Europa torus model. While characterization of these sources is a topic of current debate, we construct the best estimate based on existing literature. In particular, Smyth and Marconi (2006) conducted a two-dimensional kinetic model study, constrained by observations, of the Europa source and the subsequent spatial distributions of the neutrals. They determined escape rates of ∼2.2 × 1026 O per second, ∼2.7 × 1026 O2 per second, and ∼2 × 1027 H2 per second, produced from Europa's O2 and H2 atmosphere. Cassidy et al. (2013) examined Europa's sputtered atmosphere in more detail and derived a production rate of ∼2 × 1026 H2 per second and ∼1 × 1026 O2 per second. However, while they examined the generation of the sputtered atmosphere (from ∼2 × 1027 H2O per second), they did not determine escape resulting from charge exchange. Dols et al. (2016) reported higher source rates for O2 (∼3 × 1027 O2 per second) as a result of symmetric charge exchange with  using a two-dimensional multi-species chemistry model. (They also state this rate could be a factor of 2–3 smaller based on assumed parameters.) This result, though, does not appear to include photodissociation, which, when combined with our calculations for electron-impact dissociation, has at least a factor of 3–4 higher interaction rate than symmetric charge exchange. It appears that Europa atmospheric dissociation of O2 into two O atoms could compete with molecular oxygen charge exchange. Therefore, while we consider the possible impacts of lower and higher source rates, as reported by Cassidy et al. (2013) and Dols et al. (2016), we apply the source rates reported by Smyth and Marconi (2006) for our model.
using a two-dimensional multi-species chemistry model. (They also state this rate could be a factor of 2–3 smaller based on assumed parameters.) This result, though, does not appear to include photodissociation, which, when combined with our calculations for electron-impact dissociation, has at least a factor of 3–4 higher interaction rate than symmetric charge exchange. It appears that Europa atmospheric dissociation of O2 into two O atoms could compete with molecular oxygen charge exchange. Therefore, while we consider the possible impacts of lower and higher source rates, as reported by Cassidy et al. (2013) and Dols et al. (2016), we apply the source rates reported by Smyth and Marconi (2006) for our model.
The velocity distribution of ejected neutrals is critical. For the H2 source, we apply the Smyth and Marconi (2006) upward flux that combines a 120 K Maxwell–Boltzmann thermal core with a non-thermal tail at higher velocities. However, they only applied a mono-energetic velocity of 2.5 km s−1 for ejected O. Therefore, we apply a velocity distribution with a 2.5 km s−1 core and a high energy tail. Furthermore, they assumed the O2 direct escape rate was small and did not consider charge exchange of O ejected by dissociation. Subsequently, Dols et al. (2016) estimated the average ejection velocity for O2 due to symmetric charge exchange as 4.7 km s−1, which we use here as a core centered at ∼4.7 km s−1.
5. Ambient Plasma Environment
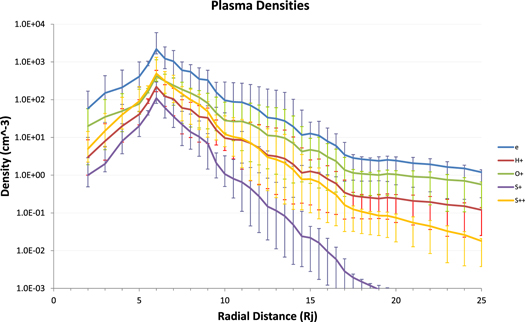
The next step in constructing a neutral torus model is characterizing the ambient plasma environment that limits neutral lifetimes and produces fast neutrals by charge exchange. While we are primarily concerned with the ion-neutral collisions near Europa's orbit (Table 3), we also consider the competing processes discussed previously in order to accurately model the entire neutral tori distribution. Below we discuss the magnetospheric plasma composition, density, and temperature which determine particle interaction rates, using the current understanding of these distributions as well as their variability by combining available observations. Therefore, we conducted a survey of Galileo Plasma Science (PLS) plasma moments (in the NASA Planetary Data System) where the spacecraft was within 1° of Jupiter's equatorial plane and no satellites were nearby. From these data, we produced a radial distribution of plasma densities, velocities, and temperatures for minimum density, average density, and maximum density conditions. We then applied the densities and relative ion abundances determined by Steffl et al. (2004), Smyth et al. (2011), Bagenal et al. (2015), and Yoshioka et al. (2017). Finally, we compared our results to the complete survey of Galileo plasma data presented in Bagenal et al. (2016). After slight adjustments, our derived plasma distribution is consistent with all reported observations. Figure 3 shows the final plasma density distribution that we use in our model.
Figure 3. Plasma densities (cm−3) as a function of radial distance from Jupiter synthesized from Galileo PLS moments with Steffl et al. (2004), Smyth et al. (2011), Bagenal et al. (2015), Yoshioka et al. (2017), and Bagenal et al. (2016). Vertical bars represent the minimum and maximum values. Data is for H+ (red), O+ (green), S+ (purple), S++ (orange), and electrons (blue). Data is within 1° of Jupiter's equatorial plane, and the minimum and maximum values are intended to capture the variation caused by plasma sheet variations resulting from Jupiter's ∼10° magnetic field axis tilt.
Download figure:
Standard image High-resolution imageUsing the plasma values in Figure 3, we next simulate the interaction processes producing a Europa torus. Therefore, we calculated interaction rates with the ambient neutrals based on low, average, and high plasma conditions, as indicated in Figure 3. We calculate the interaction rates at all radial distances, but Table 4 only shows the relevant interaction rates along Europa's orbit used in our model to illustrate the relative significance of each process. This table shows that electron-impact ionization and dissociation are the dominate particle loss processes for H2, electron-impact ionization is the dominate H loss process, electron-impact ionization and photo/electron-impact dissociation are key loss processes for O2, and electron-impact ionization is the dominant O loss process. Depending on the specific plasma conditions, dominant processes can have lifetimes as short as 2–3 days up to longer than a week. An interesting and surprising result of these calculations is that electron-impact interactions in the high plasma density environment are actually lower than the average environment. This is caused by the applied relatively low (10 eV) core electron temperature, which is below most interaction cutoff energies, while the average environment energy (20 eV) facilitates more interactions (Bagenal et al. 2015). This result highlights the large impact that electron core energies have in this region.
Table 4. Interaction Rates (Per Second) for Low, Average and High Plasma Conditions at Europa's Orbit (∼9.4 Rj)
| Low | Average | High | Reference | |
|---|---|---|---|---|
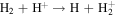
|
8.0E-08 | 1.4E-07 | 2.7E-07 | Tawara et al. (1985) |
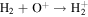 + O + O |
1.0E-07 | 2.7E-07 | 5.1E-07 | Tawara et al. (1985) |
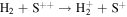
|
3.8E-08 | 1.1E-07 | 2.1E-07 | Vance & Bailey (1966) |
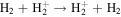
|
2.9E-08 | 9.1E-08 | 1.8E-07 | Tawara et al. (1985) |
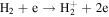
|
1.5E-06 | 4.1E-06 | 2.9E-06 | Straub et al. (1996) |
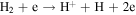
|
9.6E-08 | 2.1E-07 | 7.8E-08 | Straub et al. (1996) |

|
3.2E-07 | 1.6E-06 | 3.5E-06 | Chung et al. (1975) |
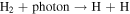
|
5.1E-09 | 5.1E-09 | 5.1E-09 | Huebner & Mukherjee (2015) |
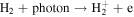
|
3.1E-09 | 3.1E-09 | 3.1E-09 | Huebner & Mukherjee (2015) |

|
6.9E-10 | 6.9E-10 | 6.9E-10 | Huebner & Mukherjee (2015) |
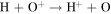
|
1.8E-07 | 5.4E-07 | 9.6E-07 | Lindsay & Stebbings (2005) |
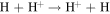
|
8.2E-08 | 2.5E-07 | 5.2E-07 | Lindsay & Stebbings (2005) |
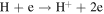
|
1.1E-06 | 3.0E-06 | 2.5E-06 | Shah et al. (1987) |

|
4.5E-09 | 4.5E-09 | 4.5E-09 | Huebner & Mukherjee (2015) |
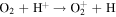
|
4.8E-11 | 9.2E-10 | 1.9E-09 | Luna et al. (2005) |
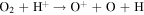
|
4.8E-11 | 9.2E-10 | 1.9E-09 | Luna et al. (2005) |
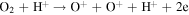
|
9.7E-10 | 7.4E-09 | 1.5E-08 | Luna et al. (2005) |
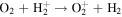
|
4.8E-11 | 9.2E-10 | 1.9E-09 | Luna et al. (2005) |
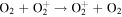
|
3.0E-07 | 8.4E-07 | 1.5E-06 | Stebbings et al. (1963) |

|
3.8E-08 | 1.7E-07 | 4.2E-07 | Luna et al. (2005) |
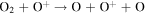
|
5.6E-08 | 1.9E-07 | 3.7E-07 | Luna et al. (2005) |
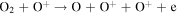
|
2.4E-08 | 7.7E-08 | 1.3E-07 | Luna et al. (2005) |
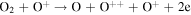
|
1.9E-09 | 8.0E-09 | 1.9E-08 | Luna et al. (2005) |
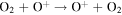
|
7.4E-09 | 2.6E-08 | 5.5E-08 | Luna et al. (2005) |
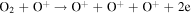
|
1.8E-08 | 8.2E-08 | 2.1E-07 | Luna et al. (2005) |
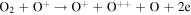
|
1.0E-08 | 3.9E-08 | 8.4E-08 | Luna et al. (2005) |
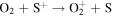
|
9.2E-11 | 6.5E-10 | 1.0E-09 | Luna et al. (2005) |
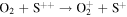
|
3.9E-08 | 1.2E-07 | 2.3E-07 | Luna et al. (2005) |
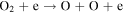
|
9.5E-07 | 3.5E-06 | 4.4E-06 | Cosby (1993) |
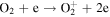
|
2.3E-06 | 5.4E-06 | 3.3E-06 | Itikawa (2009) |
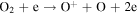
|
1.0E-06 | 2.0E-06 | 7.5E-07 | Itikawa (2009) |

|
6.6E-09 | 6.9E-09 | 1.0E-09 | Itikawa (2009) |
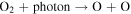
|
2.0E-07 | 2.0E-07 | 2.0E-07 | Huebner & Mukherjee (2015) |
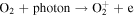
|
3.0E-08 | 3.0E-08 | 3.0E-08 | Huebner & Mukherjee (2015) |
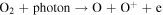
|
8.5E-09 | 8.5E-09 | 8.5E-09 | Huebner & Mukherjee (2015) |
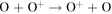
|
3.0E-07 | 9.1E-07 | 1.6E-06 | Lindsay & Stebbings (2005) |
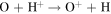
|
7.0E-08 | 1.4E-07 | 2.9E-07 | Lindsay & Stebbings (2005) |
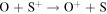
|
1.8E-09 | 3.5E-09 | 3.7E-09 | McGrath & Johnson (1989) |
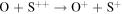
|
3.5E-08 | 1.0E-07 | 1.6E-07 | McGrath & Johnson (1989) |
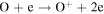
|
2.2E-06 | 5.1E-06 | 3.5E-06 | Johnson et al. (2005) |
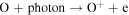
|
1.7E-08 | 1.7E-08 | 1.7E-08 | Huebner & Mukherjee (2015) |
Note. Cross section references are included in the last column. Photon interaction rates are for average solar conditions.
Download table as: ASCIITypeset image
6. Europa and Io Neutral Torus Modeling
The provided results enable us to construct a three-dimensional model of the neutral tori based on available observations and previous modeling thereby determining the spatial distribution of relevant neutrals. Using this model, we produce column densities associated with the line of sight ENA observations. This in turn allows us to determine to what extent the observed ENAs were produced by a Europa-generated neutral torus as a means of placing constraints on its scale and composition.
In order to accomplish these goals, we apply our 3D Monte Carlo neutral particle model to simulate Jovian neutral particle populations. This model was validated (Smith 2006) and successfully applied to multiple Saturn magnetospheric studies (Smith et al. 2004, 2007, 2008, 2010). It has been improved and adapted to the Jovian system, which required adjusting magnetospheric and satellite physical parameters, as well as changing the particle species and interaction rates. This 3D Monte Carlo particle tracking model is capable of simulating millions of test particles over multi-year periods. At each time step, a group of representative (weighted) particles are ejected from the relevant neutral particle sources. During each subsequent time step, these particles are subjected to the gravitational effects of Jupiter and all major satellites, as well as particle interaction processes, including electron-impact ionization and dissociation, photo-ionization and photodissociation, recombination, charge exchange, neutral–neutral collisions, collision with Jupiter and its satellites, and escape from the Jovian system. As source molecules are dissociated, the model creates resulting daughter particles that are also added to the magnetospheric particle population.
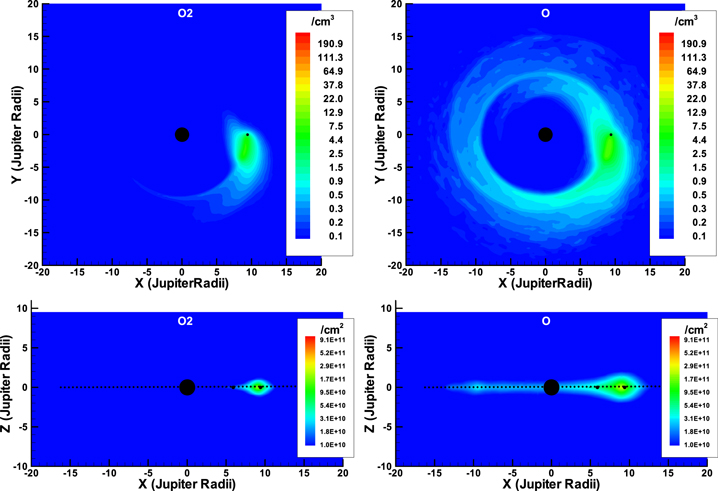
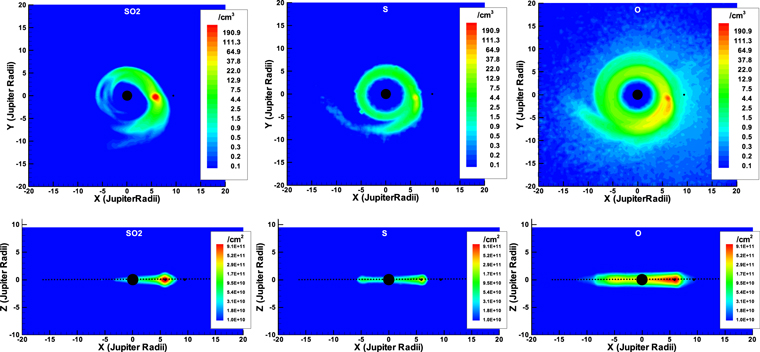
Our Europa torus model applies average plasma conditions in order to produce the average expected neutral torus. Based on Smyth and Marconi (2006), the three primary neutral source species are H2, O2, and O (ejected H2O tends to return and freeze on the surface). The Europa source rates used here are 2 × 1027H2/s, 2.7 × 1026 O2/s and 2.2 × 1026 O/s. We allow these particles to be isotropically ejected from Europa's surface with the Smyth and Marconi (2006) velocities addressed previously. Minor species, such as Na or K, are ignored, as their abundances are too low to impact our results. Over the course of a run, the ejected neutrals form an extended exospheric distribution around Europa, and their escape and/or subsequent interaction with the ambient plasma results in a model Europa neutral torus. We simulated a period of >90 days (25.5 Europa orbits), which, based on the interaction rates in Table 4 and model output monitoring, is more than enough time for the torus densities to stabilize. Figure 4 shows the resulting spatial morphology of the Europa-generated H2 and resulting H distributions, and Figure 5 shows the corresponding result for the Europa-generated O2 and O distributions. Notice that the relatively short interaction times produce asymmetric hydrogen tori and incomplete oxygen tori. The presence of atomic H in the Europa torus is supported by Roth et al.'s (2017) far-ultraviolet observations of Europa's atmosphere. These results show Europa-generated neutral torus particle distributions.
Figure 4. Europa-generated H2 (left panels) and H (right panels) model particle distributions. Top panels are densities (cm−3) as in the XY plane (−Y axis points toward the Sun and perpendicular to Jupiter's rotational (Z) axis, X axis is orthogonal to the YZ plane) in Jovian radii (Rj). Bottom panels are line of sight column densities (cm−2) through the XZ plane in Jovian radii (Rj).
Download figure:
Standard image High-resolution imageFigure 5. Europa-generated O2 (left panels) and O (right panels) model particle distributions. Top panels are densities (cm−3) as in the XY plane (−Y axis points toward the Sun and perpendicular to Jupiter's rotational (Z) axis, X axis is orthogonal to the YZ plane) in Jovian radii (Rj). Bottom panels are line of sight column densities (cm−2) through the XZ plane in Jovian radii (Rj).
Download figure:
Standard image High-resolution imageWe next executed the same model with similar constraints, except we replaced the Europa source with an Io source of SO2 with a nominal rate of 1000 kg s−1. This species is assumed to isotropically eject from Io's exobase (∼700 km above the surface) with a thermal velocity distribution (core of ∼515 m s−1) and a high energy (power law) velocity tail. The SO2 in Io's exosphere is removed by charge exchange or dissociation with the products populating its neutral torus. Table 5 shows the particle lifetimes at Io's orbit. Figure 6 shows the model particle spatial distributions (using average plasma conditions) for the SO2 and the resulting O and S Io-generated tori. Note these results are qualitatively similar to Smyth and Marconi (2003).
Figure 6. Io-generated SO2 (left panels), S (middle panels), and O (right panels) model particle distributions. Top panels are densities (cm−3) as in the XY plane (−Y axis points toward the Sun and perpendicular to Jupiter's rotational (Z) axis, X axis is orthogonal to the YZ plane) in Jovian radii (Rj). Bottom panels are line of sight column densities (cm−2) through the XZ plane in Jovian radii (Rj).
Download figure:
Standard image High-resolution imageTable 5. Neutral Particle Lifetimes (in Hours) for Low, Average, and High Plasma Conditions at Io's Orbit (∼5.9 Rj)
| Interaction lifetime (hours) | ||||
|---|---|---|---|---|
| Process | Low | Average | High | Reference |
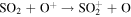
|
1034 | 494 | 180 | Luna et al. (2005) |
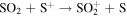
|
935005 | 455473 | 125237 | Luna et al. (2005) |
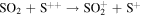
|
789 | 390 | 112 | Luna et al. (2005) |
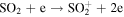
|
23 | 61 | 226 | Lindsay et al. (1996) |
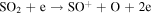
|
39 | 137 | 1242 | Lindsay et al. (1996) |
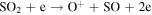
|
815 | 8053 | 56916 | Lindsay et al. (1996) |
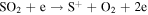
|
246 | 1123 | 18612 | Basner et al. (1995) |
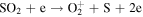
|
403 | 1393 | 14700 | Basner et al. (1995) |
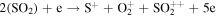
|
183 | 1510 | 28239 | Lindsay et al. (1996) |
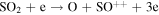
|
56980 | 1052300 | 2171258 | Lindsay et al. (1996) |

|
4093 | 4093 | 4093 | Huebner & Mukherjee (2015) |
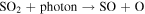
|
45 | 45 | 45 | Huebner & Mukherjee (2015) |
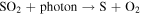
|
131 | 131 | 131 | Huebner & Mukherjee (2015) |
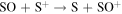
|
298 | 206 | 69 | Luna et al. (2005) |
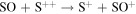
|
137 | 89 | 30 | Luna et al. (2005) |
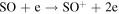
|
10 | 23 | 187 | Rajvanshi & Baluja (2010) |
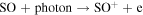
|
5267 | 5267 | 5267 | Huebner & Mukherjee (2015) |
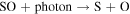
|
12 | 12 | 12 | Huebner & Mukherjee (2015) |
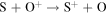
|
227 | 244 | 104 | McGrath & Johnson (1989) |
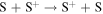
|
104 | 111 | 47 | McGrath & Johnson (1989) |
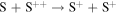
|
77 | 77 | 32 | McGrath & Johnson (1989) |
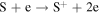
|
6 | 13 | 43 | Freund et al. (1990) |
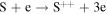
|
2663 | 42713 | 4989327 | Freund et al. (1990) |
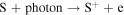
|
2572 | 2572 | 2572 | Huebner & Mukherjee (2015) |
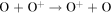
|
74 | 69 | 28 | Lindsay & Stebbings (2005) |
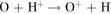
|
227 | 336 | 125 | Lindsay & Stebbings (2005) |
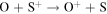
|
6251 | 14363 | 9191 | McGrath & Johnson (1989) |
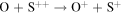
|
342 | 430 | 190 | McGrath & Johnson (1989) |
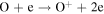
|
48 | 195 | 1250 | Johnson et al. (2005) |
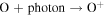
|
16581 | 16581 | 16581 | Huebner & Mukherjee (2015) |
Note. Cross section references are included in the last column. Photon interaction rates are for average solar conditions.
Download table as: ASCIITypeset image
The provided simulations show that primary source species neutral tori in Jupiter's magnetosphere tend to be asymmetric, due to the relatively large plasma interaction rates and low initial velocity distributions, while some derivative species (H and O) tend to form more complete tori due to the dissociation energies and scattering. The geometry of our Io-generated neutral oxygen torus is consistent with Japanese Space Agency Hisaki Mission (Yoshikawa et al. 2014) neutral oxygen observations by Koga et al. (2017, 2018).
7. Model Analysis and Discussion
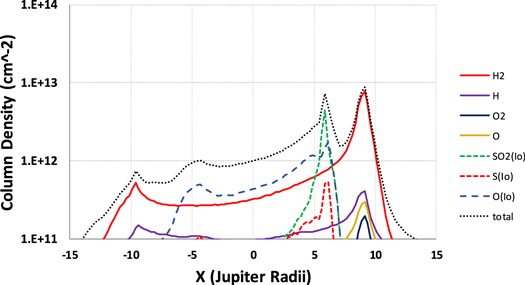
The provided simulations help illustrate the relative spatial distributions of Io and Europa-generated neutrals. In Figure 7, we combine all of the model results to show the relative contribution of each neutral species to the total Jovian neutral torus. In this figure, both Io and Europa are in the XZ plane (i.e., perpendicular to the line of site along the equatorial plane or Z = 0, −Y points toward the observer) with Io at X = +5.9 Rj and Europa at X = +9.4 Rj. In effect, we are representing the perpendicular line of sight column through the Jovian system in the equatorial plane. Similar to Smyth and Marconi (2006), this figure shows that while the larger Io source dominates close to its orbit, these neutral densities drop off rather quickly at further distances from Jupiter until neutrals from Europa start to dominate. At Europa's orbit, H2 from this moon is by far the dominate species. However, unlike Smyth and Marconi (2006), we have applied a much more accurate plasma distribution, along with more comprehensive particle interaction processes. We show that Io torus densities drop off much faster with radial distance from Jupiter than the Europa neutral torus, which starts to dominate as close as ∼6.7 Rj to Jupiter. Thus we confirmed by direct simulation that the neutrals ejected from Io do not survive long enough to populate the Europa torus region. We also show that SO2 from Io dominates the Io neutral torus, while neutral sulfur is relatively minor due to its high ionization rate (Table 5). Figure 7 also illustrates the asymmetry of the neutral tori, as densities are much larger near the source moons (+X axis) as compared to the opposite side of the orbit (−X axis).
Figure 7. Model equatorial model column densities (cm−2) as a function of distance from Jupiter (Rj): Europa H2 (solid red), Europa H (solid purple), Europa O2 (solid black), Europa O (solid yellow), Io SO2 (dashed green), Io O (dashed blue), Io S (dashed red), and all species combined (dotted black). The data represent a time when both Io and Europa are in the XZ Plane (i.e., perpendicular to the line of site along the equatorial plane or Z = 0, −Y points toward the observer) with Io at X = +5.9 Rj and Europa at X = +9.4 Rj. This confirms that the Io-generated neutrals do not contribute significantly at Europa's orbit.
Download figure:
Standard image High-resolution imageFor the Europa torus, we determine that the spatially integrated hydrogen (H2 + H) and oxygen (O + O2) populations are ∼1.4 × 1033 and ∼2.1 × 1032, respectively. Our values are a factor of ∼3.1 smaller for hydrogen and ∼1.9 smaller for oxygen than those of Smyth and Marconi (2006). Similarly, from Io, our model total torus content is ∼1.5 × 1033 for oxygen and ∼3.1 × 1032 for sulfur, which is a factor of ∼2.1 lower and ∼2.6 lower, respectively, than those of Smyth and Marconi (2006). At Europa's orbit, our model produces an average neutral particle density of ∼26.6 particles cm−3, which compares favorably with the previous reported values of 20–50 cm−3 (Lagg et al. 2003). As mentioned previously, because the tori are highly asymmetric, average values do not represent the actual spatial density variations.
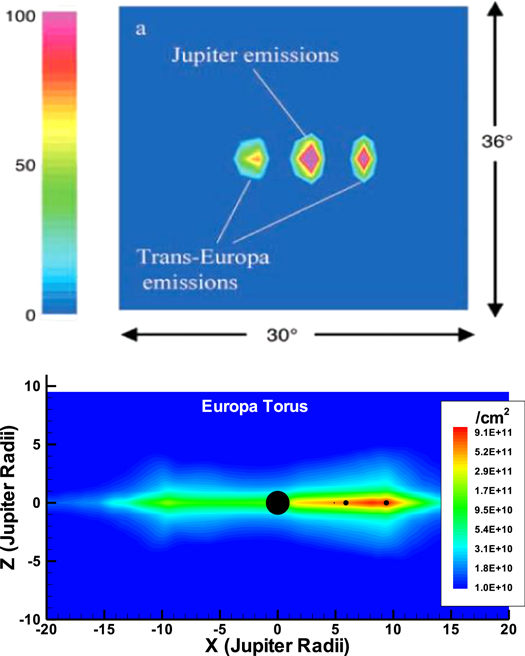
Based on the results of these simulations, we can now assess the likelihood that the Mauk et al. (2003) ENA observations were produced by a Europa torus. The ENA observations were accumulated (or summed) over 15 hr, during which Europa covered ∼18% of its orbit. To replicate the source for this image in our model, we summed up the model line of sight column densities over the same 15 hr period (with Europa in similar locations to the Mauk et al. 2003 observations). As shown in Figure 7, Io-generated neutral densities are too low to impact observations in the vicinity of the Europa torus, so the location of Io does not impact these results. Figure 8 compares the Europa neutral line of sight column density (lower panel) with the ENA observations (upper panel) for the same geometry and integration time as in Mauk et al. (2004). Since the H+ charge exchange cross sections for neutrals vary slowly at the energies of interest, the line of sight integrated ENA observational counts are proportional to model column densities. This figure shows that the predicted Europa torus is qualitatively well correlated with the ENA observations near Europa's orbit. The Mauk et al. observations show emissions from Jupiter; however, our model does not contain a Jupiter atmospheric source because it does not impact the torus and therefore does not affect our results.
Figure 8. Comparison of model Europa torus (bottom) to the ENA observations. (a) At the top, from Mauk et al. (2004), the color scale represents detector counts, with pink indicating 1450 counts over 15 hr of accumulation within 1 4 × 1
4 × 1 9 bins, which roughly equated to relative column density. (b) Europa torus model is the summed line of sight column densities (cm−2) through the XZ plane in Jovian radii (Rj) for all four species (H2, H, O2, and O). The model torus was produced to match Mauk et al. (2004) observational conditions (i.e., ∼15 hr integration period with similar Europa locations, which covers about 18% of its orbit).
9 bins, which roughly equated to relative column density. (b) Europa torus model is the summed line of sight column densities (cm−2) through the XZ plane in Jovian radii (Rj) for all four species (H2, H, O2, and O). The model torus was produced to match Mauk et al. (2004) observational conditions (i.e., ∼15 hr integration period with similar Europa locations, which covers about 18% of its orbit).
Download figure:
Standard image High-resolution imageAdditionally, at distances closer to Jupiter than Europa's orbit, the Mauk et al. observations do not show emissions because there are very limited incident 50–80 keV H+ in this region to produce ENAs. In particular, Paranicas et al. (2009), show ion intensities as a function of radial distance from Jupiter. Moving toward Jupiter at approximately 9.5 Rj (near Europa's orbit), the 30 and 100 keV proton intensities rapidly drop by more than one to two orders of magnitude and continue to decrease by another two orders of magnitude toward Io's orbit. Since these protons are producing the observed ENAs, the ENA flux should also decrease by multiple orders of magnitude, thus explaining the lack of detected ENA emissions closer to Jupiter. While there are neutral particles in this region (as shown by our model), there are not enough incident 50–80 keV H+ to produce detectable ENA emissions. Paranicas et al. (2009) also indicate the initial decrease in ion fluxes near Europa's orbit is likely caused by loss to the neutral gas torus at Europa's orbit. They further state that if charge exchange is the dominant loss for these ions, then ion loss to the satellite's surface is greatly reduced.
We now examine the contribution to ENAs due to the energetic H+ plasma ion interactions with the plasma torus. We do this using the data in Figure 2 for low, medium, and high plasma environments, and compare the results to those for H+ charge exchange with our simulated Europa neutral torus. The neutral torus interaction rates are derived from the data in Figure 1 and the results in Figures 4–6, which provide more realistic neutral particle densities. In order to capture the range of possible torus densities, we also executed all of the provided model runs with minimum and maximum plasma conditions. Table 6 shows our modeled peak Europa neutral torus densities near Europa (right ansa) and at the furthest point in the orbit from Europa (left ansa). With low plasma density conditions, Europa torus peak densities increased by 7% for the right ansa and 71% for the left ansa. The models with high plasma density conditions showed that Europa torus peak densities decreased from average conditions by 29% for the right ansa and 26% for the left ansa.
Table 6. Model Europa Torus Densities (in cm−3) for Low, Average, and High Plasma Conditions
| Model peak neutral densities (cm−3) | ||||
|---|---|---|---|---|
| Species | Low | Avg | High | |
| Near Europa | H | 68.6 | 30.5 | 48.0 |
| H2 | 1173.4 | 1137.0 | 770.0 | |
| O | 15.6 | 11.4 | 12.4 | |
| O2 | 10.8 | 6.5 | 7.3 | |
| 180° away | H | 2.1 | 1.7 | 2.0 |
| H2 | 7.8 | 5.2 | 3.1 | |
| O | 2.5 | 0.6 | 0.4 | |
| O2 | 0.6 | 0.1 | 0.1 | |
Note. Data presented for near Europa (right ansa) and on the other side of the orbit (left ansa, or 180° away) for H, H2, O, and O2.
Download table as: ASCIITypeset image
Having determined more accurate Europa neutral torus densities, we calculated the charge exchange rates with neutrals as well as plasma. These interaction rates yield relative production values used to produce Table 7, which reveals the percentage contribution of each species to this observed ENA image. Because the local plasma conditions during Mauk et al.'s (2003) observations are not known, we present the results for the entire range of plasma conditions (i.e., low, average, and high). Results are given for the right and left ansas. Similarly, we calculate the percentage contributions to the left and right ansas from H+ interaction with the plasma. The data presented in this table confirm the presence of a Europa neutral torus. In the densest portion of the torus (right ansa in the ENA image), 98.7%–99.8% of the ENA emissions are caused by neutrals in the Europa torus. On the other side of the torus (left ansa in the ENA image), the torus densities are much smaller and a greater percentage of the ENA emissions are generated by H+ interacting with ions in the plasma. Depending on the ambient plasma conditions, only ∼31% to ∼85% of the ENAs are produced by a Europa neutral torus. Table 7 also shows that H2 is producing almost all of the ENAs near Europa (right ansa), while O becomes a much more significant contributor far from the moon. This table also helps illustrate that the total ENA emissions appear more symmetric than the primary neutral torus (H2) because of contributions from atomic oxygen and hydrogen that are more spread out, as is the plasma. Oza et al. (2018) report a possible Sun angle dependence on O2 source location. In such a case, the particles would not be ejected isotropically, and the oxygen torus distribution could be impacted. However, this is not expected to impact the results in Table 7, as oxygen has a relatively minor impact on the ENA observations. However, we intend to verify this assumption in future research.
Table 7. Relative Species Contribution (of 50–80 keV ENA Production) to the Mauk et al. (2003) ENA Image for Near Europa (Left Ansa) and Far from Europa (Right Ansa) for Low, Average, and High Ambient Plasma Conditions
| Left Ansa | Low | Average | High | Right Ansa | Low | Average | High |
|---|---|---|---|---|---|---|---|
| S+ | 1.3% | 3.9% | 5.8% | S+ | 0.0% | 0.0% | 0.1% |
| S++ | 3.8% | 11.5% | 17.3% | S++ | 0.0% | 0.1% | 0.3% |
| S+++ | 0.1% | 0.4% | 0.6% | S+++ | 0.0% | 0.0% | 0.0% |
| O+ | 9.2% | 27.8% | 42.4% | O+ | 0.1% | 0.3% | 0.8% |
| O++ | 0.5% | 1.6% | 2.4% | O++ | 0.0% | 0.0% | 0.0% |
| H | 6.5% | 6.5% | 6.4% | H | 2.7% | 1.3% | 2.9% |
| H2 | 48.2% | 39.9% | 19.9% | H2 | 93.5% | 95.7% | 91.9% |
| O | 22.7% | 6.8% | 3.8% | O | 1.8% | 1.4% | 2.2% |
| O2 | 7.7% | 1.6% | 1.3% | O2 | 1.8% | 1.1% | 1.8% |
| Plasma torus | 14.9% | 45.2% | 68.6% | Plasma torus | 0.2% | 0.5% | 1.3% |
| Neutral torus | 85.1% | 54.8% | 31.4% | Neutral torus | 99.8% | 99.5% | 98.7% |
Note. Total contribution for the plasma and neutral tori at Europa's orbit are also shown. Note the Io neutral torus does not contribute to the observations of the torus at Europa's orbit (Figure 7).
Download table as: ASCIITypeset image
The previous results show that, based on source rate assumptions, the ENA observations require a Europa neutral torus. We used the best current estimates for Europa source rates to produce these results, but further work could allow us to place better constraints on these source rates. We re-executed our previously provided Europa models and iteratively lowered the Europa source rates to assess their impact on our results. Even after lowering the source rates by three orders of magnitude, the Europa neutral torus still produces ∼7%–34% of the ENAs in the brightest region of the image. Such low source rates are far below even the lowest estimates (Shemansky et al. 2014), which further verifies the presence of a Europa-generated neutral torus. While we applied the Smyth and Marconi (2006) Europa source rates, we also examined the potential impact of the more extreme models for the source rates. Cassidy et al. (2013) reported 2 × 1026H2/s and 1 × 1026 O2/s, which are respectively about a factor of 10 and 4 lower than our assumed rates. However, these rates are still much higher than the minimum source rates provided previously and would not impact our conclusions. In terms of larger reported source rates, Dols et al. (2016) report a Europa source rate of ∼2.9 × 1027 O2/s (resulting from symmetric molecular oxygen charge exchange), which would produce O at almost an order of magnitude larger than our oxygen source rate. However, our interaction rate calculations (Table 4) indicate that dissociation of O2 into two neutral oxygen atoms is a factor of 3.4–4.4 larger than O2 symmetric charge exchange. Thus, while this process might be important and was considered in our calculations, charge exchange of O (produced by dissociation) should dominate over O2 in producing ENAs.
Since we show that the ENA emissions reported by Mauk et al. (2003) are likely to be produced at least partially by a Europa-generated neutral torus, they can in principal provide insight into activity from the moon. In this research, we do not address proposed transient activity or the temporal variability from the Jupiter magnetic field axial tilt. Based on the unsuccessful attempts of Roth et al. (2016) to reimage possible Europa plumes, it appears unlikely that an eruption occurred during the Mauk et al. (2003) observations, and even if one was occurring, it would only serve to enhance the Europa torus and therefore not impact our conclusions. However, in the future, we will extend our research to include smaller timescale phenomena, which will help with the interpretation of future observations.
8. Summary
In this paper, we combined Jupiter data analysis with simulations to examine the possibility that the Mauk et al. (2003) observations indicate the presence of a Europa-generated neutral torus. We produced 3D models of the Europa and Io neutral tori based on available observations for low, average, and high density ambient plasma populations. The resulting spatial distributions of neutrals for the dominant species throughout the magnetosphere were then used to re-interpret the ENA measurements. Major findings of our research include:
- 1.These simulations confirmed that a Europa neutral torus is required to quantitatively account for the ENA observations.
- 2.We calculated density constraints for H, H2, O, and O2 in the Europa neutral torus.
- 3.The Europa neutral tori are highly asymmetric. Near Europa, ∼99% of the brightest portion of the ENA image was produced by a Europa neutral torus. Furthest from Europa, on the opposite side of the orbit, ∼15%–69% of the ENA emissions are likely due to interaction of H+ with the ambient plasma. This emphasizes that one cannot assume that ENAs are produced only through charge exchange interactions with neutrals.
- 4.At least 7%–34% of the Mauk et al. (2003) observed ENAs would be produced by Europa neutrals, even with a three order of magnitude reduction in the source rate (<2 × 1024 s−1), which is well below all reported Europa source rate estimates.
- 5.Source rate changes take longer to impact the Europa neutral torus than the Io neutral torus. The dominant processes at Europa's orbit have lifetimes of at least 2–3 days up to longer than a week, while at Io, the neutral particles start interacting in 8–13 hr. Additionally, the range in observable ambient plasma environments can vary particle interaction rates by more than an order of magnitude.
These results confirm Europa is an important source of neutrals in Jupiter's magnetosphere and suggest future ENA observations by spacecraft can be used to better observe Europa's activity and, possibly, its habitability.
This work is supported by NASA Contract NAS5-97271 Task Order 003 and the NASA Solar System Workings Program.