Abstract
The Earth and other rocky planets and planetesimals in the solar system formed through the mixing of materials from various radial locations in the solar nebula. This primordial material likely had a range of oxidation states as well as bulk compositions and volatile abundances. We investigate the oxygen fugacity produced by the outgassing of mixtures of solid meteoritic material, which approximate the primitive nebular materials. We find that the gas composition and oxygen fugacity of binary and ternary mixtures of meteoritic materials vary depending on the proportion of reduced versus oxidized material, and also find that mixtures using differentiated materials do not show the same oxygen fugacity trends as those using similarly reduced but undifferentiated materials. We also find that simply mixing the gases produced by individual meteoritic materials together does not correctly reproduce the gas composition or oxygen fugacity of the binary and ternary mixtures. We provide tabulated fits for the oxygen fugacities of all of the individual materials and binary mixtures that we investigate. These values may be useful in planetary formation models, models of volatile transport on planetesimals or meteorite parent bodies, or models of trace element partitioning during metal-silicate fractionation.
Export citation and abstract BibTeX RIS
1. Introduction
Rocky planets can acquire atmospheres through a variety of processes, including capture of nebular gas (e.g., Sasaki 1990), devolatilization of impactors during accretion (e.g., Schaefer & Fegley 2010; Kuwahara & Sugita 2015), and volcanic outgassing (e.g., Abe 2011; Carlson et al. 2014; Fegley & Schaefer 2014). These atmospheres can be strongly modified by other processes such as hydrodynamic escape (e.g., Lammer et al. 2014; Ormel et al. 2015), impact erosion (e.g., Liu et al. 2015; Schlichting et al. 2015), photochemistry (Hu et al. 2012), geochemical cycles (Abbot et al. 2012), and biogenic reactions (Kasting & Siefert 2002), among others. In order to determine the degree to which each of these processes has influenced the evolution of these atmospheres, it is important to determine relevant initial conditions from which models can begin. Discovery of new, unexpected types of rocky extrasolar planets also emphasizes the need to determine the possible range of atmospheric initial compositions in order to help distinguish the action of abiotic processes from biogenic ones if we ever hope to identify a true biosignature.
Accretion models for the Earth and other terrestrial planets predict that they formed from materials derived from a range of radial distances in the inner solar nebula. Mixing models using meteoritic materials as solar nebula proxies have been extensively used to determine the bulk composition of the Earth and the origin of the Earth's volatiles, and have also been applied to other solar system bodies like Mars and Vesta. In these models, more reducing meteoritic materials are assumed to form closer to the Sun, whereas more oxidizing materials like carbonaceous chondrites are thought to form at larger radial distances. For instance, Lodders & Fegley (1997a) modeled the bulk composition of Mars by looking at three component meteorite mixtures that reproduce the oxygen isotopic signature of the shergottite-nahklite-chassignite (SNC) meteorites. They found the bulk composition in terms of FeO in silicate, metal, and sulfide through simple redox reactions. Similar models have been done for the howardite–eucrite–diogenite (HED) parent body (e.g., Moynier & Fegley 2015), Earth (e.g., Burbine & O'Brien 2004; Javoy et al. 2010), and various individual meteorites and meteoritic components (e.g., Boesenberg 2003; Zanda et al. 2006). Evidence from short-lived radioisotope chronometers as well as dynamical models of planet formation indicate that igneous differentiation on planetesimals and embryos may have been complete before the terrestrial planets were assembled. Therefore, some component of the Earth's building blocks may have already been differentiated before they were accreted.
Atmospheric formation was likely a continuous process during accretion, with both outgassing of the growing planets' interior as well as impact degassing of accreting planetesimals contributing to the growing atmosphere. Elkins-Tanton & Seager (2008) determined the ranges of atmospheric mass for large terrestrial planets by looking at meteoritic volatile compositions, bulk iron content, and simple redox reactions, which were assumed to go to completion (e.g., water + Fe metal = FeO). They looked at single meteorite compositions and did not consider complex chemical interactions among the components in determining the atmospheric compositions. In our previous work, we determined the chemical compositions of outgassed atmospheres by assuming equilibrium between gas and solid phases and using average compositions for different meteoritic classes (e.g., carbonaceous, ordinary and enstatite chondrites) (Schaefer & Fegley 2007, 2010). Calculations by Hashimoto et al. (2007) for outgassed atmospheres from CI chondrites give similar results.
In this paper, we continue to explore the range of atmospheric compositions that can be derived from the primitive materials of the solar nebula. In particular, we explore the oxygen fugacities of different meteoritic materials and their mixtures. We include a range of reduced and oxidized chondritic materials as well as achondritic material, representative of volatile-depleted differentiated planetesimals. Our calculations are generally applicable to both impact degassed and outgassed atmospheres.
We suggest that these models are applicable to the initial atmospheric compositions of rocky bodies in the solar system and of rocky bodies in exoplanetary systems with solar or near-solar metallicity. The composition of planet-forming materials in a protoplanetary disk is primarily dependent on the elemental bulk composition and temperature, with pressure being a secondary influence. This was demonstrated in the 1970s in pioneering papers (e.g., see Figure 1 of Barshay & Lewis 1976 and Figures 5 and 7 of Barshay & Lewis 1976). The effect of radial sampling on the bulk composition of rocky planets was first explored by Barshay (1981) and considered much later in the astronomical community (e.g., Morbidelli et al. 2000; Bond et al. 2010a, 2010b; Elser et al. 2012; Thiabaud et al. 2014). Condensation chemistry changes in non-solar metallicity systems once the C/O elemental ratio is about unity. At this point, a new suite of chemically reduced condensates (e.g., graphite (C), silicon carbide (SiC), niningerite (MgS), cohenite (Fe3C), and oldhamite (CaS)) appears, and the condensation temperatures of oxide and silicate minerals drop by hundreds of degrees. The effect of variable C/O ratio on the chemistry of planet-forming materials was first described by Gilman (1969), Larimer and his colleagues (Larimer 1975; Larimer & Bartholomay 1979), and subsequently by Lodders & Fegley (1997b). As quantitatively discussed by Prinn & Fegley (1989), thermochemical reactions were the dominant processes in the solar nebula with photochemistry, radioactivity, and lightning being less important (see pp. 85–92 of their paper). Accretional heating, heating by radioactive decay, dry and wet thermal metamorphism, and igneous differentiation on planetary bodies should proceed according to the same basic chemical and physical principles that govern these processes in our solar system. Therefore, the models presented here should be useful for predicting the range of oxidation states of initial outgassed atmospheres on rocky bodies in extrasolar planetary systems as well as in our solar system.
Oxygen fugacity, along with temperature and pressure, also has a controlling influence on chemical processes within a planet or planetestimal's mantle such as trace element partitioning during core formation (Hillgren 1991; Holzheid et al. 1994; Righter et al. 1997). By exploring the range of oxygen fugacities that can be produced by mixtures of meteoritic material, we can explore the range of conditions that could exist in natural systems during core formation. Our fits for oxygen fugacity for different mixtures of meteoritic material can then be used in models of trace element partitioning. These may be particularly useful in modeling planetesimals and meteorite parent bodies where the effect of pressure on partitioning coefficients is small.
In Section 2, we describe our thermochemical model and give the compositions of the meteoritic materials used in our calculations. We show their oxygen fugacities as a function of temperature and pressure. We furthermore show that simple linear mixing models of gases from individual meteoritic materials do not correctly reproduce the equilibrium gas composition of binary and ternary mixtures when heterogeneous equilibrium (i.e., gas–solid equilibrium) is considered. This is particularly important if results are to be used in partitioning models. Therefore, separate calculations must be made for each mixture composition. In Section 3, we show the calculated oxygen fugacities of binary and ternary mixtures of meteoritic materials. Finally, we discuss the application of these results to terrestrial planets and planetesimals. We provide tabulated linear regression coefficients for the oxygen fugacities of binary mixtures. Grids of values for the ternary mixtures are available upon request.
2. Methods
This section is organized as follows. In Section 2.1, we discuss our thermochemical equilibrium models and the temperature and pressure parameters used in these calculations. In Section 2.2, we discuss our choices of meteoritic material types, which are motivated by planet formation scenarios, and their compositions.
2.1. Thermochemical Equilibrium Models
As in our previous work, we use a Gibbs energy minimization code of the type described by van Zeggeren & Storey (1970) to calculate thermochemical equilibrium of meteoritic materials. The input parameters for this code are the bulk elemental composition of the system, temperature, and total pressure. Given these parameters, the code simultaneously calculates the equilibrium abundances of all stable solid phases and gas compounds while maintaining mass balance. Our calculations consider 18 major rock-forming elements, minor elements, and volatiles in chondritic material (Al, C, Ca, Cl, Cr, F, Fe, H, K, Mg, Mn, N, Na, O, P, S, Si, and Ti). Elemental compositions of the meteoritic materials used in the calculations are given in Table 1 and discussed further in the following section. We use the IVTANTHERMO database (Belov et al. 1999), supplemented with thermodynamic data for complex oxides and silicates commonly found in meteorites from Robie & Hemingway (1995) and Holland & Powell (2011). The final database used here contains 978 compounds (225 solid, 754 gas). In our nominal calculations, solid compounds are assumed to be pure phases, rather than solid solutions, although we discuss how using solid solutions can affect the results. The use of pure phases is done for comparison with our previous work, as well as to make the computation tractable.
Table 1. Compositions of Meteoritic Materials Used in Calculations
| Element | CIa | CVb | Hc | EHd | Eucritee |
|---|---|---|---|---|---|
| H (ppm) | 19730 | 22.4 | 459 | 1309 | 85 |
| C (ppm) | 34800 | 2700 | 1200 | 4100 | 18 |
| N (ppm) | 2948 | 80 | 34 | 560 | 0.453 |
| O (wt%) | 46.225 | 37.07 | 33.46 | 28.51 | 42.8 |
| F (ppm) | 58.2 | 56 | 27 | 191 | 19 |
| Na (ppm) | 4990 | 3185 | 6454 | 7493 | 2800 |
| Mg (wt%) | 9.595 | 14.82 | 14.12 | 10.54 | 4.0 |
| Al (wt%) | 0.858 | 1.73 | 1.24 | 0.77 | 7.1 |
| Si (wt%) | 10.57 | 15.96 | 17.06 | 16.48 | 23.0 |
| P (ppm) | 924 | 1090 | 1135 | 2269 | 397 |
| S (wt%) | 5.35 | 2.14 | 1.94 | 5.18 | 0.15 |
| Cl (ppm) | 700 | 290 | 77 | 615 | 18 |
| K (ppm) | 543 | 250 | 830 | 913 | 222 |
| Ca (wt%) | 0.9076 | 1.88 | 1.21 | 0.68 | 7.7 |
| Ti (wt%) | 0.0439 | 0.096 | 0.07 | 0.03 | 0.38 |
| Cr (ppm) | 2630 | 3620 | 3216 | 3216 | 2090 |
| Mn (ppm) | 1920 | 1550 | 2323 | 1936 | 3990 |
| Fe (wt%) | 18.347 | 23.54 | 27.52 | 33.15 | 14.5 |
| Co (ppm) | 507 | 599 | 800 | 794 | 4 |
| Ni (wt%) | 1.067 | 1.41 | 1.70 | 1.82 | 0.00047 |
| Total | 99.94 | 99.99 | 99.98 | 99.50 | 100.59 |
Notes.
aCI: Orgueil (Lodders 2003). bCV: Allende (Jarosewich et al. 1987), N (Lodders & Fegley 1997a), O increased within error to provide best match.
cH: average (Schaefer & Fegley 2007).
dEH: Indarch, bulk (Wiik 1956), C (Moore & Lewis 1966), N (Moore & Gibson 1969; Grady et al. 1986), Cl (Wiik 1969; Garrison et al. 2000), F (Fisher 1963; Reed 1964).
eEucrite: Juvinas, bulk (Wänke et al. 1972), S, P (Kitts & Lodders 1998), H (average of two analyses; Duke & Silver 1967; Yanai & Kojima 1995), C (Grady et al. 1997), N (Miura & Sugiura 1993).
match.
cH: average (Schaefer & Fegley 2007).
dEH: Indarch, bulk (Wiik 1956), C (Moore & Lewis 1966), N (Moore & Gibson 1969; Grady et al. 1986), Cl (Wiik 1969; Garrison et al. 2000), F (Fisher 1963; Reed 1964).
eEucrite: Juvinas, bulk (Wänke et al. 1972), S, P (Kitts & Lodders 1998), H (average of two analyses; Duke & Silver 1967; Yanai & Kojima 1995), C (Grady et al. 1997), N (Miura & Sugiura 1993).
Download table as: ASCIITypeset image
Calculations are done for a range of temperature and pressure conditions simulating planetary outgassing and atmosphere–surface equilibrium. Equilibrium calculations for individual meteoritic materials are done at temperatures ranging from 300 to 2000 K at a nominal pressure of 1 bar. All binary and ternary mixtures are calculated at the nominal pressure of 1 bar and temperature of 1500 K, which is within the observed range of basaltic lava eruption temperatures and therefore applicable to planetary volcanic outgassing.
We find small variations (<0.1 log units) in oxygen fugacity with total pressure up to several kilobars, equivalent to the deep crust or upper mantle on the Earth or central pressures of large planetesimals. The pressure dependence is small because the change in the molar volume of solid phases, which buffer the oxygen fugacity, is relatively small. Campbell et al. (2009) measured the pressure effect on two metal-oxide oxygen fugacity buffers and found that at the pressures found in the upper mantle, the oxygen fugacity increased by about 0.3–0.4 log units per GPa at 1500 K. As pressure increases, the difference in molar volume between the metal and oxide phases decreases, resulting in an increase in the oxygen fugacity.
2.2. Selection of Meteoritic Compositions and Mixtures
In this paper, we consider the outgassing of mixtures of different types of meteoritic materials, both chondritic and achondritic. The chondrites are undifferentiated (i.e., unmelted) stony meteorites containing metal, sulfide, and silicate phases. Geochemical data show that the Earth has an approximately chondritic composition, although it cannot be identified with any single chondritic group (e.g., Jagoutz et al. 1979; Hart & Zindler 1986; Kargel & Lewis 1993; Lodders & Fegley 1997a; Palme & O'Neill 2014). For example, Jagoutz et al. (1979) analyzed a suite of six carefully selected ultramafic nodules from alkali basalts for major, minor, and trace elements. They reached several major conclusions. Quoting their paper (Jagoutz et al. 1979; pg. 2039): "These [ultramafic] nodules with compositions near the intersection of the geochemical and cosmochemical trend lines in Figure 2 have chondritic element ratios of compatible refractory elements. Thus, a mantle composition fixed at this unfractionated point of intersection seems to be a plausible choice for a primitive mantle, bearing in mind that neither the geochemical nor the cosmochemical trend line of Figure 2 are extremely well defined. There are however, several possibilities which could change Si or Si and Mg concentrations but would leave the refractory element ratios unchanged."
Figure 1, which is a modified version of their figure, shows that all the primitive mantle compositions summarized by Palme & O'Neill (2014, their Table 3 and that of Kargel & Lewis 1993) fall inside the rectangle near the intersection of the two fractionation lines proposed by Jagoutz et al. (1979). The red star shows the mean values (Mg/Si = 1.05 ± 0.03 and Al/Si 0.10 ± 0.01) from an unweighted average of the nine BSE compositions (all those in Table 3 of Palme & O'Neill 2014 and Kargel & Lewis 1993). As noted by Jagoutz et al. (1979), the high Mg/Si ratio of the BSE may be due to evaporative loss of Si from the Earth, removal of some Si into Earth's core, or may be an artifact due to different Mg/Si ratios in Earth's upper and lower mantles (Ringwood 1958; Anderson 1977; Ringwood & Kesson 1977). This issue remains unresolved but computations of silica dissolution in Earth's primordial steam atmosphere, Si isotopic measurements, and an enstatite chondrite model for the Earth (e.g., Georg et al. 2007; Javoy et al. 2010; Fegley et al. 2016) support each of the three alternatives. Palme & O'Neill (2014) discuss the bulk Earth Fe/Mg ratio and conclude it is ∼2.1–2.2, higher than the CI chondritic value. The ∼10% differences between Earth's Mg/Si and Fe/Mg ratios and those of the major chondrite groups may reflect its accretion from a yet unknown type of chondritic material, our uncertain knowledge of lower mantle and core composition, or another elemental fractionation during the Moon-forming impact. In any case, we conclude Earth's bulk composition is chondritic to first approximation (within ∼10%) and thus use chondritic meteorites as proxies for the nebular material accreted by Earth during its formation.
Figure 1. Mg/Si ratios vs. Al/Si ratios of unfractionated meteorites and terrestrial ultramafic nodules. Adapted from Jagoutz et al. (1979). The red rectangle highlights the possible composition of the primitive mantle summarized by Palme & O'Neill (2014). The yellow star is the mean value for the Bulk Silicate Earth.
Download figure:
Standard image High-resolution imageBoyet & Carlson (2005) reported a 20 ppm excess in  /
/ in ancient terrestrial rocks relative to chondritic meteorites. Decay of the short-lived radionuclide
in ancient terrestrial rocks relative to chondritic meteorites. Decay of the short-lived radionuclide  (half-life 103 Ma and now extinct) produces
(half-life 103 Ma and now extinct) produces  , and the reported excess originated within 30 Ma of the formation of the solar system. The
, and the reported excess originated within 30 Ma of the formation of the solar system. The  excess apparently required a Sm/Nd ratio larger than chondritic for the accessible silicate Earth. Thus, several groups suggested either a
excess apparently required a Sm/Nd ratio larger than chondritic for the accessible silicate Earth. Thus, several groups suggested either a  -depleted reservoir in the lower mantle or the loss of such a reservoir to space via collisional erosion; see Campbell & O'Neill (2012), Boyet & Carlson (2005), Caro et al. (2008), and, O'Neill & Palme (2008). However, recent work by Burkhardt et al. (2016) shows that after correction for nucleosynthetic Nd isotopic heterogeneity, the
-depleted reservoir in the lower mantle or the loss of such a reservoir to space via collisional erosion; see Campbell & O'Neill (2012), Boyet & Carlson (2005), Caro et al. (2008), and, O'Neill & Palme (2008). However, recent work by Burkhardt et al. (2016) shows that after correction for nucleosynthetic Nd isotopic heterogeneity, the  /
/ ratios of chondrites and the accessible silicate Earth are indistinguishable within ∼5 ppm, the current level of analytical precision. Consequently, the long-standing paradigm of a chondritic Sm/Nd ratio for the bulk Earth still holds. In turn, this means the bulk Earth is probably chondritic for all refractory lithophile elements, as long argued by Wänke and colleagues (e.g., Wänke 1981 and references therein).
ratios of chondrites and the accessible silicate Earth are indistinguishable within ∼5 ppm, the current level of analytical precision. Consequently, the long-standing paradigm of a chondritic Sm/Nd ratio for the bulk Earth still holds. In turn, this means the bulk Earth is probably chondritic for all refractory lithophile elements, as long argued by Wänke and colleagues (e.g., Wänke 1981 and references therein).
Hafnium-tungsten dating of achondrites suggests that igneous differentiation of planetesimals occurred within the first 10 Myr of solar system formation (Jacobsen et al. 2008; Kleine et al. 2009). Other radioisotopic systems provide similar timelines (e.g., Wadhwa et al. 2009). Additionally, dynamical models of planetary accretion also suggest that the terrestrial planets accreted from a number of protoplanets of varying degrees of differentiation, which have been processed and reprocessed by impact events (e.g., Asphaug 2010). Burbine & O'Brien (2004) determine that very few combinations of chondritic materials are able to reproduce the major chemical composition of the Earth, which they suggest means that either the Earth is primarily composed of materials not represented by known chondritic material, or substantial Si has been sequestered into the Earth's core.
Table 1 lists the meteoritic materials that we include in our calculations. We select compositions for two carbonaceous chondrites (CI, CV), one ordinary chondrite (H), one enstatite chondrite (EH), and one achondrite (eucrite). We chose these meteoritic types because they sample the diversity of known stony meteorite types. As discussed above, the Earth's bulk composition can be approximated by mixing of at least one of these reducing components with small amounts of one or more carbonaceous chondrites (e.g., Lodders 1991; Lodders & Fegley 1997a; Lodders 2000; Warren 2011; Fitoussi & Bourdon 2012).
Rather than explore all known carbonaceous chondrites, we have chosen to focus on CI and CV chondritic materials. Although CI chondrites experienced extensive aqueous alteration on their parent body, they are considered the most compositionally primitive of carbonaceous chondrites and provide the best match to solar photospheric abundances (Lodders 2003). They are also the most oxidized of all meteoritic materials as measured by the distribution of Fe among metal, silicates, and oxides (Krot et al. 2014). CV chondrites are less oxidized than CI chondrites but may also have experienced some degree of aqueous alteration. The CV chondrites are subdivided into an oxidized and a reduced group based on the ratio of metal to magnetite abundances, as well as the nickel content of metal and sulfides. The best characterized CV chondrite is Allende, which is a member of the oxidized group. We use the selected abundances of the Orgueil CI chondrite, which is the best characterized of the CI chondrites, from Lodders (2003). For the CV chondrite, we use the reference model bulk composition of the Allende meteorite determined by Jarosewich et al. (1987), which includes H as chemically bound water and carbon. Jarosewich et al. (1987) do not determine the N abundance of Allende, so we use the average abundance of N in CV chondrites from Lodders & Fegley (1997a).
We also consider ordinary and enstatite chondritic material. As we showed in Schaefer & Fegley (2007), the gas compositions and oxygen fugacity for the different ordinary chondrite groups (H, L, and LL) are very similar to one another, so we only consider H chondrites here, using the average composition determined in our previous paper. This average composition includes all petrographic types from H3 to H6. Volatile abundances (H, C, N) in the unequilibrated type 3s are larger than those for the higher petrographic types, so this average composition represents a somewhat volatile-poor H chondrite composition. Enstatite chondrites are the most reduced of the major chondritic meteorite groups. We only consider EH chondrites here, in particular the Indarch EH4 chondrite for its well-characterized volatile abundances (see Table 1). Note that while enstatite chondrites are reduced, they are known to be very volatile rich, which is why the H, C, and N abundances are larger than those of the H chondrite (Grady et al. 1986; Robert 2003). EL chondrites would likely give similar results, but volatile abundances are relatively poorly characterized.
Finally, we chose as a representative achondritic meteoritic material the Juvinas eucrite. Eucrites are the most abundant type of achondrite and have basaltic compositions. They are members of the HED meteorite family, which are all believed to derive from the asteroid 4 Vesta. Juvinas is a brecciated monomict eucrite, which has been well characterized (Kitts & Lodders 1998). Calculations for representative howardites and diogenites produced results very similar to the results for Juvinas, and so are not shown here. While the very low volatile abundances of eucrites indicates that the Earth cannot be built solely from differentiated materials, mixtures of these differentiated materials with the volatile-rich chondrites may approximate the Earth's volatile inventory.
We do not consider iron or stony-iron meteoritic materials because volatile element abundances in these meteorites are poorly constrained.
3. Results
In the remainder of this paper, we will primarily focus on the oxygen fugacity4
of the meteoritic materials and their mixtures. The oxygen fugacity ( ) affects both the gas chemistry and the bulk mineralogy. The relative abundances of the major gases (e.g.,
) affects both the gas chemistry and the bulk mineralogy. The relative abundances of the major gases (e.g.,  /
/ , CO/
, CO/ ) can be calculated from the oxygen fugacity of the gas, as we discuss later. The bulk mineralogy can also be related to oxygen fugacity buffers. Iron- and carbon-bearing solid species are particularly important in controlling the oxygen fugacity. The common redox buffers we compare to are nickel–nickel oxide:
) can be calculated from the oxygen fugacity of the gas, as we discuss later. The bulk mineralogy can also be related to oxygen fugacity buffers. Iron- and carbon-bearing solid species are particularly important in controlling the oxygen fugacity. The common redox buffers we compare to are nickel–nickel oxide:
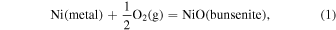
quartz−fayalite−magnetite (QFM):
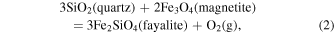
wüstite−magnetite (WM):
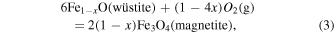
iron−wüstite (IW):
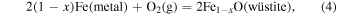
and quartz−fayalite−iron (QFI):
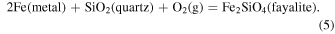
The data for these fugacity buffers are taken from the IVTANTHERMO database for consistency, but is very similar to the thermodynamic data from other sources (e.g., Robie & Hemingway 1995; Holland & Powell 2011). In the following sections, we first discuss the  of the individual meteoritic material, then their binary and ternary mixtures. We will discuss results for all possible binary mixtures of the five meteoritic components, although we will focus primarily on the mixtures involving CI chondritic material. We consider ternary mixtures of the two carbonaceous chondritic components with the reducing components.
of the individual meteoritic material, then their binary and ternary mixtures. We will discuss results for all possible binary mixtures of the five meteoritic components, although we will focus primarily on the mixtures involving CI chondritic material. We consider ternary mixtures of the two carbonaceous chondritic components with the reducing components.
3.1. Oxygen Fugacities of Individual Meteoritic Material Components
Traditionally, the relative oxidation state of meteoritic types is determined by the distribution of Fe among its three common oxidation states: metal (0),  -bearing oxides and silicates (e.g.,
-bearing oxides and silicates (e.g.,  in olivine and
in olivine and  in pyroxene), and
in pyroxene), and  -bearing oxides and silicates (e.g., magnetite, hematite, laihunite; Rubin et al. 1988; Krot et al. 2014). This can be described by a Urey–Craig diagram, which plots the abundance of Fe in metal and sulfides versus the abundance of Fe in silicates and oxides (all normalized to Si). By this ranking, the oxidation state decreases from CI > CV > H > EH (Rubin et al. 1988).
-bearing oxides and silicates (e.g., magnetite, hematite, laihunite; Rubin et al. 1988; Krot et al. 2014). This can be described by a Urey–Craig diagram, which plots the abundance of Fe in metal and sulfides versus the abundance of Fe in silicates and oxides (all normalized to Si). By this ranking, the oxidation state decreases from CI > CV > H > EH (Rubin et al. 1988).
Figure 2 shows the oxygen fugacities of the meteoritic materials in Table 1 as a function of temperature in comparison to solid state buffers. The regression coefficients for the polynomial fits are given in Table 2. Our calculations agree with the ranking of oxidation states for chondritic meteorites on the basis of Fe oxidation state discussed above. We find that the eucritic material, which is not included in the above ranking, has the same  as the enstatite chondritic material.
as the enstatite chondritic material.
Figure 2. Oxygen fugacity of individual meteoritic components as a function of temperature compared with standard buffers. QFM = quartz−fayalite−magnetite, WM = wüstite−magnetite, IW = iron−wüstite, QFI = quartz−fayalite−iron. Meteoritic material compositions are given in Table 1 and the regressions for  of the meteoritic materials are given in Table 2.
of the meteoritic materials are given in Table 2.
Download figure:
Standard image High-resolution imageTable 2.
Oxygen Fugacity Fits for Individual Meteoritic Materials as a Function of Temperature (log10  = a +
= a +  /T +
/T +  /T2 +
/T2 +  /T3 +
/T3 +  /T4) at 1 bar Total Pressure
/T4) at 1 bar Total Pressure
| Meteoritic Material | a | b | c | d | f | r2 |
|---|---|---|---|---|---|---|
| CI | 2.4976 | −9.8605 | −17.0701 | 7.5220 | −1.0404 | 0.9998 |
| CV | 9.0621 | −31.193 | 5.1092 | −1.8475 | 0.2000 | 0.9996 |
| H | 5.0743 | −22.906 | −5.6610 | 2.0634 | −0.2618 | 0.9999 |
| EH | 4.9495 | −24.024 | −4.6236 | 1.7177 | −0.2332 | 0.9999 |
| Eucrite | 5.4856 | −25.127 | −3.6580 | 1.3014 | −0.1650 | 0.9999 |
Note. Fits are computed for temperatures from 300 to 2000 K.
Download table as: ASCIITypeset image
Opaque mineral assemblages found in chondrules, CAIs, and matrix in CV chondrites provide a record of the temperature and  of the parent body during post-accretionary alteration. These mineral assemblages include Ni-rich metal and Ni-poor magnetite. The Ni-poor magnetite is thought to have formed by oxidation of the metal phase during aqueous alteration of the parent body (Choi et al. 1997). The
of the parent body during post-accretionary alteration. These mineral assemblages include Ni-rich metal and Ni-poor magnetite. The Ni-poor magnetite is thought to have formed by oxidation of the metal phase during aqueous alteration of the parent body (Choi et al. 1997). The  of these conditions was constrained by McMahon et al. (1980) and Blum et al. (1989) to a region between the pure iron−magnetite buffer and a buffer defined by
of these conditions was constrained by McMahon et al. (1980) and Blum et al. (1989) to a region between the pure iron−magnetite buffer and a buffer defined by  metal and magnetite. We found that the nominal Allende standard reference model (Jarosewich et al. 1987) did not match this buffer, so we varied the Fe and O abundances until we calculated a matching
metal and magnetite. We found that the nominal Allende standard reference model (Jarosewich et al. 1987) did not match this buffer, so we varied the Fe and O abundances until we calculated a matching  and found both Ni-rich metal and magnetite to be stable. Note that to do this, we used ideal solid solutions for a mixture of Fe and Ni, which we use in all of our calculations. Our final Fe abundance of 23.54 wt% agrees well with the mean value of 23.55 ± 0.16 wt% given in Jarosewich et al. (1987). No recommended total oxygen abundance is given, but we calculate a mean value from all of the given analyses of 37.10 with a standard deviation of 1.24 wt%. Our final oxygen abundance of 37.07 wt% matches the average value very well. Including additional ideal solid solutions for the silicate phases reduces the
and found both Ni-rich metal and magnetite to be stable. Note that to do this, we used ideal solid solutions for a mixture of Fe and Ni, which we use in all of our calculations. Our final Fe abundance of 23.54 wt% agrees well with the mean value of 23.55 ± 0.16 wt% given in Jarosewich et al. (1987). No recommended total oxygen abundance is given, but we calculate a mean value from all of the given analyses of 37.10 with a standard deviation of 1.24 wt%. Our final oxygen abundance of 37.07 wt% matches the average value very well. Including additional ideal solid solutions for the silicate phases reduces the  of the CV chondrite by 0.5–0.7 log units between 1000 and 1500 K.
of the CV chondrite by 0.5–0.7 log units between 1000 and 1500 K.
As we showed in Schaefer & Fegley (2007), our calculations of the  for ordinary chondritic material are in very good agreement with the intrinsic oxygen fugacity measurements of Brett & Sato (1984). In contrast, McSween & Labotka (1993) looked at variations in the Fe abundance in different minerals as a function of petrographic type in ordinary chondrites and found evidence for systematic oxidation at higher petrographic types. They speculated that a reaction such as the ferrosilite−iron−fayalite (FIF) buffer,
for ordinary chondritic material are in very good agreement with the intrinsic oxygen fugacity measurements of Brett & Sato (1984). In contrast, McSween & Labotka (1993) looked at variations in the Fe abundance in different minerals as a function of petrographic type in ordinary chondrites and found evidence for systematic oxidation at higher petrographic types. They speculated that a reaction such as the ferrosilite−iron−fayalite (FIF) buffer,
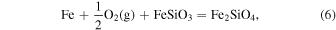
was responsible for the progressive oxidation of Fe. They calculated the  for these minerals to be 2 log units below the intrinsic oxygen fugacity measurements of Brett & Sato (1984) at 1000 K. The trends have slightly different slopes, so they are less discrepant when extrapolated to the higher temperatures measured by Brett & Sato (1984). In contrast, ours agree very well with the measurements, and in fact our calculated
for these minerals to be 2 log units below the intrinsic oxygen fugacity measurements of Brett & Sato (1984) at 1000 K. The trends have slightly different slopes, so they are less discrepant when extrapolated to the higher temperatures measured by Brett & Sato (1984). In contrast, ours agree very well with the measurements, and in fact our calculated  corresponds very closely to the FIF buffer. Including olivine and orthopyroxene solid solutions in our calculations, rather than pure phases, does cause our calculated
corresponds very closely to the FIF buffer. Including olivine and orthopyroxene solid solutions in our calculations, rather than pure phases, does cause our calculated  to decrease by ∼1–1.4 log units. This agrees with the lower bounds of the intrinsic
to decrease by ∼1–1.4 log units. This agrees with the lower bounds of the intrinsic  measurements of Brett & Sato (1984), but is still higher than the calculations of McSween & Labotka (1993). As we discussed in our previous paper, McSween & Labotka (1993) used an equilibrium constant for the FIF buffer that gives a lower
measurements of Brett & Sato (1984), but is still higher than the calculations of McSween & Labotka (1993). As we discussed in our previous paper, McSween & Labotka (1993) used an equilibrium constant for the FIF buffer that gives a lower  than the IVTAN database. Compared to our present calculations, their FIF buffer is ∼0.5 log units lower than ours at 1200 K. Raising their calculated
than the IVTAN database. Compared to our present calculations, their FIF buffer is ∼0.5 log units lower than ours at 1200 K. Raising their calculated  by this amount brings their calculations into good agreement with our solid solution calculations, as we should expect.
by this amount brings their calculations into good agreement with our solid solution calculations, as we should expect.
Berthet et al. (2009) did partial melting experiments at 1 GPa on the Indarch EH4 chondrite and on samples with 2–6 wt% Si metal added to the Indarch EH4 bulk composition. The  of the natural Indarch EH4 sample was about IW−1, in agreement with our calculations for the same bulk composition. The
of the natural Indarch EH4 sample was about IW−1, in agreement with our calculations for the same bulk composition. The  values of their artificially reduced samples—containing excess elemental Si—reached IW−5 log units. We also did calculations for an Indarch EH4 composition plus 2 wt% Si and found
values of their artificially reduced samples—containing excess elemental Si—reached IW−5 log units. We also did calculations for an Indarch EH4 composition plus 2 wt% Si and found  values 9–10 log bar units lower than the Indarch EH4 material, far lower than the values reported by Berthet et al. (2009). Other partial melting experiments by McCoy et al. (1999) suggest that the intrinsic
values 9–10 log bar units lower than the Indarch EH4 material, far lower than the values reported by Berthet et al. (2009). Other partial melting experiments by McCoy et al. (1999) suggest that the intrinsic  of Indarch is near the Cr–
of Indarch is near the Cr– buffer, which is at about IW−6 at 1500 K. This is different than that reported by Berthet et al. (2009) for their Indarch EH4 sample. Including the silicate solid solutions reduces the
buffer, which is at about IW−6 at 1500 K. This is different than that reported by Berthet et al. (2009) for their Indarch EH4 sample. Including the silicate solid solutions reduces the  of our calculations by 1.2–1.3 log units to about IW−2.5.
of our calculations by 1.2–1.3 log units to about IW−2.5.
There are no measurements of intrinsic oxygen fugacity for eucritic material, although there have been measurements for diogenites, a closely related meteoritic type. Petrographic studies indicated that the presence of metallic iron and small amounts of hematite indicated that the eucrites formed at much lower oxygen fugacities than terrestrial basalts. Hewins & Ulmer (1984) measured  for two diogenites, which they found to be around the IW buffer. Partial melting experiments have suggested that eucrites formed by partial melting of a carbonaceous chondrite under reducing conditions of about IW−1 (Stolper 1977; Jurewicz et al. 1993, 1995). Other achondrites have both higher (angrites: IW + 1) and lower (aubrites: IW−5) redox conditions (Wadhwa 2008). Our results are consistent with the partial melting experiments for eucritic material, giving
for two diogenites, which they found to be around the IW buffer. Partial melting experiments have suggested that eucrites formed by partial melting of a carbonaceous chondrite under reducing conditions of about IW−1 (Stolper 1977; Jurewicz et al. 1993, 1995). Other achondrites have both higher (angrites: IW + 1) and lower (aubrites: IW−5) redox conditions (Wadhwa 2008). Our results are consistent with the partial melting experiments for eucritic material, giving  of IW−1.4 at 1000 K to IW−0.8 at 1500 K. Including olivine and orthopyroxene solid solutions has a small effect and only reduces the
of IW−1.4 at 1000 K to IW−0.8 at 1500 K. Including olivine and orthopyroxene solid solutions has a small effect and only reduces the  by 0.2–0.4 log units.
by 0.2–0.4 log units.
3.2. Oxygen Fugacity of Binary Mixtures
In Schaefer & Fegley (2010), we speculated that the atmospheres of mixtures of meteoritic materials could be found by simple linear combinations of the atmospheres of the individual components. However, this proves to be incorrect. Figure 3 compares the major gas composition of a mixture of 10% CV chondritic material and 90% H chondritic material from calculations (solid lines) versus a linear combination (e.g.,  ) (dashed lines). Variations between the linear combination and the calculated mixture are non-uniform. At 1500 K, the abundances of
) (dashed lines). Variations between the linear combination and the calculated mixture are non-uniform. At 1500 K, the abundances of  and
and  from the linear combination are 4% and 17% lower than the abundances calculated for the mixture, whereas
from the linear combination are 4% and 17% lower than the abundances calculated for the mixture, whereas  and
and  are 2% and 75% larger, respectively. The predicted abundance of
are 2% and 75% larger, respectively. The predicted abundance of  shows the worst agreement between the two models. The lower panel compares the
shows the worst agreement between the two models. The lower panel compares the  from the calculated mixtures and the linear mixture. The linear mixture overestimates the
from the calculated mixtures and the linear mixture. The linear mixture overestimates the  at all temperatures. Variations are larger at lower temperatures. The difference between the linear combinations and calculated mixtures is due to changes in the equilibrium condensed phases.
at all temperatures. Variations are larger at lower temperatures. The difference between the linear combinations and calculated mixtures is due to changes in the equilibrium condensed phases.
Figure 3. Gas composition of a binary mixture of 10% CV chondritic material with 90% H chondritic material as a function of temperature at 1 bar. Solid lines are calculated equilibria, and dashed lines are linear mixtures of the end-member gases. The bottom panel is the difference between the calculated  and the prediction of the linear mixture model.
and the prediction of the linear mixture model.
Download figure:
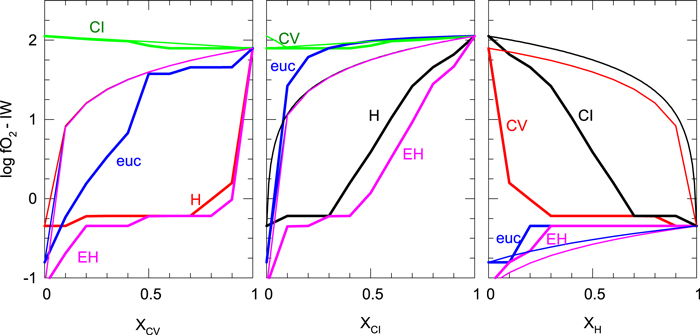
Standard image High-resolution imageFigure 4 shows the oxygen fugacities of binary mixtures as a function of composition for the nominal conditions of 1 bar and 1500 K, relative to the iron−wustite (IW) buffer. The x-axis gives the mole fraction of CV (left), CI (center), or H (right) chondritic material present in the binaries. Note that some binaries appear on two of the panels (e.g., CI–CV appear left and center). The bold lines show the results of equilibrium calculations, whereas the thin lines are the result of linear mixing of the end components. The two carbonaceous chondritic materials have similar oxygen fugacities, and their binary shows a relatively smooth transition in oxygen fugacity from CI to CV. The linear mixing results agree fairly well with the calculated values.
Figure 4. Oxygen fugacity of binary mixtures. The left panel shows binaries with the CV chondrite, the middle panel shows binaries with the CI chondrite, and the right panel shows binaries with the H chondrite, where the x-axes give the molar fraction of that component in the mixture. Lines in each panel are labeled with the second component of the binary mixtures (e.g., in the left panel, line marked CI refers to the CI–CV binary; in the right panel. it refers to the CI–H binary.) Thick lines are for the calculated equilibrium, whereas thin lines are for the calculations of the linear mixtures of the end-member gases.
Download figure:
Standard image High-resolution imageThe binaries of the carbonaceous chondritic materials with the more reducing eucritic material show a much different behavior. For these mixtures, the linear mixing results do a much poorer job of predicting the  of the binaries. The binaries of CI and CV with the eucritic material remain at the
of the binaries. The binaries of CI and CV with the eucritic material remain at the  of the carbonaceous chondritic material for greater than ∼20% CI in the mixture, whereas for the CV–eucritic material mixture, the
of the carbonaceous chondritic material for greater than ∼20% CI in the mixture, whereas for the CV–eucritic material mixture, the  drops when there is less than 50% CV. The linear mixing model underpredicts the
drops when there is less than 50% CV. The linear mixing model underpredicts the  for the CI binary, but overpredicts for the CV binary.
for the CI binary, but overpredicts for the CV binary.
The binaries of the H and EH chondritic material with the carbonaceous chondritic materials show a different behavior from the binaries with the eucritic material. These binaries remain at the  of the reduced component up to relatively high fractions of carbonaceous chondritic material before they abruptly increase. This indicates a reduced buffering system of minerals. The transition between low and high
of the reduced component up to relatively high fractions of carbonaceous chondritic material before they abruptly increase. This indicates a reduced buffering system of minerals. The transition between low and high  is much more sudden for CV binaries than for CI binaries. The linear mixing model strongly overpredicts the
is much more sudden for CV binaries than for CI binaries. The linear mixing model strongly overpredicts the  for all compositions. The binaries of H chondritic material with eucritic and EH chondritic material hold steady at the H chondritic material
for all compositions. The binaries of H chondritic material with eucritic and EH chondritic material hold steady at the H chondritic material  across most of the compositional range, again indicating possible buffering by the FIF buffer. The linear mixing model underpredicts the
across most of the compositional range, again indicating possible buffering by the FIF buffer. The linear mixing model underpredicts the  of these mixtures.
of these mixtures.
As can be seen, linear mixtures do a poor job of estimating the oxygen fugacity of the binary mixtures when one of the components is metal bearing (e.g., H, EH). The eucrites are known to contain significantly less metal (<0.5 wt%, Duke 1965) than the H (∼16 wt%) and EH (∼24 wt%) chondrites.
Figure 5 shows the oxygen fugacity of the CI–H binary mixtures as a function of temperature compared to standard buffers. The numbers on the curves indicate the mole fraction of H chondritic material present in the mixture. Note that above ∼70% H chondritic material, the  of the mixture is identical to the pure H chondritic material, which is consistent with the compositional trends shown in Figure 4. The
of the mixture is identical to the pure H chondritic material, which is consistent with the compositional trends shown in Figure 4. The  of the H chondritic material is nearly linear with inverse temperature, but the
of the H chondritic material is nearly linear with inverse temperature, but the  of CI chondritic material is more closely approximated by a fourth-order polynomial. Consequently, the temperature dependence of the binary mixtures does change slightly with composition. We provide fits for the temperature dependence of the binary mixtures in Table 3.
of CI chondritic material is more closely approximated by a fourth-order polynomial. Consequently, the temperature dependence of the binary mixtures does change slightly with composition. We provide fits for the temperature dependence of the binary mixtures in Table 3.
Figure 5. Oxygen fugacity of CI–H binaries as a function of temperature. Numbers on the lines indicate the percent of H chondritic material.
Download figure:
Standard image High-resolution imageWork done on outgassed atmosphere compositions by Bukvic (1980) also looked at mixtures of CI and H chondritic materials. Bukvic reported gas compositions for mixtures of 90%–99% H chondritic material with the remainder of CI chondritic material. He found log  values at 1500 K of ∼−12 for all of the mixtures, which agrees very well with our calculations.
values at 1500 K of ∼−12 for all of the mixtures, which agrees very well with our calculations.
3.3. Oxygen Fugacity of Ternary Mixtures
The ternary systems that we consider are shown in Figure 6(a) CI–CV–H and (b) CI–CV–eucrite. These mixtures simulate the addition of volatile-rich material to a meteorite parent body or other asteroid as well as the Earth. Mixtures that substitute EH for H chondritic materials provide nearly identical results.
Figure 6. Oxygen fugacity of a CI–CV–H (left) and CI–CV–eucrite (right) ternary at 1 bar and 1500 K. Oxygen fugacities are given relative to the iron−wüstite (IW) buffer.
Download figure:
Standard image High-resolution imageFor the CI–CV–H ternary system, the mixture has the highest  when H chondritic material is less than 20% of the composition. Strong oxidation persists up to ∼40% H chondritic material, but the mixture is uniformly reduced when it contains more than ∼40% of the H chondritic material. Mixtures of CI–CV with EH chondritic material, not shown here, produce nearly identical results, with only a slight compression of the oxidized region to smaller EH contents (i.e., there is slightly more dark blue on the CI–CV–EH ternary diagram).
when H chondritic material is less than 20% of the composition. Strong oxidation persists up to ∼40% H chondritic material, but the mixture is uniformly reduced when it contains more than ∼40% of the H chondritic material. Mixtures of CI–CV with EH chondritic material, not shown here, produce nearly identical results, with only a slight compression of the oxidized region to smaller EH contents (i.e., there is slightly more dark blue on the CI–CV–EH ternary diagram).
In contrast, the CI–CV–eucritic material ternary has a uniformly high oxygen fugacity, with only a very small region of reduced conditions in the top corner near 100% eucritic material fraction. This shows, as seen in the binary diagrams of Figure 4, that the eucritic material does not exert a strong influence on the oxygen fugacity of the material. That is, for a planet that contains abundant volatiles from a carbonaceous body, addition of silicate material from a differentiated body will not strongly affect the oxidation state of the mantle or the composition of the atmosphere.
4. Relation Between Oxygen Fugacity and Atmospheric Composition
The oxygen fugacity is diagnostic of relative gas abundances. For instance, the relative abundances of H and C gases can be determined through reactions involving  (gas). For example,
(gas). For example,  /
/ and
and  /CO can be determined from
/CO can be determined from
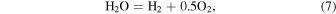
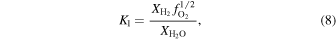
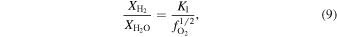

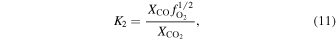
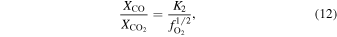
where the equilibrium constants are related to temperature via
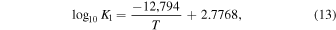
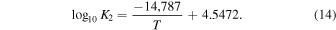
The equilibrium constants for the reactions are taken from the IVTANTHERMO database and fit for temperatures between 298.15 and 2000 K. We give equations for the oxygen fugacity of the individual meteoritic materials as a function of temperature in Table 2 and the binary mixtures in Table 3. In order to reproduce the low-temperature behavior of the gas ratios, the oxygen fugacity fits are provided as up to fourth-order polynomials in inverse temperature.
We show examples of the gas ratios  /
/ ,
,  /
/ ,
,  /
/ , and
, and  /
/ in Figures 7 and 8 for the binary mixtures of CI chondritic material with H or eucritic material. The ratios
in Figures 7 and 8 for the binary mixtures of CI chondritic material with H or eucritic material. The ratios  /
/ and
and  /
/ can be derived from the following equations:
can be derived from the following equations:
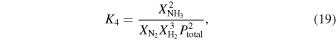
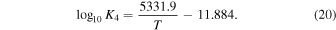
We include these ratios because they are relevant to early Earth atmosphere environments. In particular,  ,
,  ,
,  , and
, and  are favored in Miller–Urey-type scenarios of reducing early atmospheres, but are much less abundant in present-day terrestrial volcanic gases, which are much more oxidizing than Miller–Urey-type reducing atmospheres. Ammonia,
are favored in Miller–Urey-type scenarios of reducing early atmospheres, but are much less abundant in present-day terrestrial volcanic gases, which are much more oxidizing than Miller–Urey-type reducing atmospheres. Ammonia,  ,
,  ,
,  , and water vapor have strong IR bands and should be easier to observe than
, and water vapor have strong IR bands and should be easier to observe than  ,
,  , or
, or  , for which relatively weak visible lines (
, for which relatively weak visible lines ( ,
,  ) or collision-induced dipole absorption (
) or collision-induced dipole absorption ( ,
,  ,
,  ) is required to see these IR-inactive gases.
) is required to see these IR-inactive gases.
Figure 7. Ratios of the major gas abundances for the CI–H chondritic material binaries as a function of temperature. Reducing conditions produce more positive values for all of the ratios, as indicated by the red arrow. Lines are increments of 10% in the binary mixture, as shown in the legends.
Download figure:
Standard image High-resolution imageFigure 8. Ratios of major gas abundances for the CI–eucritic material binaries as a function of temperature. Bold lines are the same as for Figure 7; thin gray lines show the binaries from 5% to 1% CI chondritic material, increasing from top to bottom.
Download figure:
Standard image High-resolution imageIn Figures 7 and 8, the ratios are given so that positive values indicate more reducing conditions. The lower boundary in both figures is given by the CI chondritic material. The upper boundaries are relatively similar because the H chondritic material and the eucritic material have similarly low oxygen fugacities. For both sets of binaries, the  /
/ ratio is relatively insensitive to temperature above ∼700 K. This is true to a slightly lesser degree for
ratio is relatively insensitive to temperature above ∼700 K. This is true to a slightly lesser degree for  /
/ , which increases only slightly with temperature due to thermal dissociation. The reduced trace gases (
, which increases only slightly with temperature due to thermal dissociation. The reduced trace gases ( /
/ ,
,  /
/ ) are more sensitive to temperature and are strongly favored at low temperatures. The ratios of
) are more sensitive to temperature and are strongly favored at low temperatures. The ratios of  /
/ and
and  /
/ at low temperatures provide the greatest chance to discriminate between the oxidation state of the starting materials, as the oxidized CI material shows marked decreases in these ratios compared to the increases produced in the reduced H chondritic and eucritic materials. Note that because the Earth's upper mantle is more oxidized than CI chondritic material, the
at low temperatures provide the greatest chance to discriminate between the oxidation state of the starting materials, as the oxidized CI material shows marked decreases in these ratios compared to the increases produced in the reduced H chondritic and eucritic materials. Note that because the Earth's upper mantle is more oxidized than CI chondritic material, the  /
/ and
and  /
/ ratios of volcanic gases lie at values below those of the CI material.
ratios of volcanic gases lie at values below those of the CI material.
Figures 7 and 8 also highlight the greater reducing power of the H chondritic material in comparison to the eucritic material due to a larger carbon concentration. The lines for the binaries of eucritic material with more than 10% CI material are difficult to distinguish from one another because they lie so close together, whereas there is steady increase in the ratios for the CI–H binaries. We have included intermediate values for the eucritic material binaries to fill in the large gap between the 10% CI binary and fully eucritic material. Note that with only 1%–2% CI material in the eucritic binaries, the gas ratios resemble those for the 30% CI + 70% H material binaries. Therefore, it would be impossible to distinguish from a measured gas composition the difference between a differentiated body with very small amounts of volatile material versus a very primitive, metal-bearing body with large amounts of volatile material.
Note also that the low-temperature results are affected by the formation of volatile-bearing solid phases such as hydrated silicates. The formation of these phases has a stronger effect on abundances of the minor gas species such as  . See, for instance, the small peak in the
. See, for instance, the small peak in the  /
/ ratio of the pure H chondritic material line in Figure 7. The formation of hydrous phases has a larger effect on the mixtures with very low hydrogen abundances, such as the CI–eucrite mixtures with more than 90% eucritic material (note the large dips in the
ratio of the pure H chondritic material line in Figure 7. The formation of hydrous phases has a larger effect on the mixtures with very low hydrogen abundances, such as the CI–eucrite mixtures with more than 90% eucritic material (note the large dips in the  /
/ ratio in Figure 8). At sufficiently small CI chondritic concentrations (<3%), there is insufficient hydrogen to form hydrous phases, so that the large dips in the
ratio in Figure 8). At sufficiently small CI chondritic concentrations (<3%), there is insufficient hydrogen to form hydrous phases, so that the large dips in the  /
/ ratio at low temperature do not occur.
ratio at low temperature do not occur.
5. Oxidation State of the Mantle
5.1. Present-day Mantle
The average oxygen fugacity of Earth's present-day upper mantle is within ±2 log units of the QFM buffer (Frost & McCammon 2008). This average  is derived from several types of measurements including (1) chemical analyses of the ferric to total iron ratio in mid-ocean ridge basalts formed by partial melting of the mantle (Bézos & Humler 2005; Christie et al. 1986), (2) measured (Sato & Wright 1966; Sato et al. 1973; Benhamou et al. 1988; Rosen et al. 1993; Osadchii et al. 1997) and computed (Symonds et al. 1994)
is derived from several types of measurements including (1) chemical analyses of the ferric to total iron ratio in mid-ocean ridge basalts formed by partial melting of the mantle (Bézos & Humler 2005; Christie et al. 1986), (2) measured (Sato & Wright 1966; Sato et al. 1973; Benhamou et al. 1988; Rosen et al. 1993; Osadchii et al. 1997) and computed (Symonds et al. 1994)  of volcanic gases, (3)
of volcanic gases, (3)  computed from
computed from  /
/ -bearing mineral assemblages in fresh volcanic rocks (e.g., Section 1.3.4.3 of Basaltic Volcanism Study Project 1981; Benhamou et al. 1988), and (4)
-bearing mineral assemblages in fresh volcanic rocks (e.g., Section 1.3.4.3 of Basaltic Volcanism Study Project 1981; Benhamou et al. 1988), and (4)  calculated from
calculated from  /
/ -bearing mineral assemblages in upper mantle samples (xenoliths) from varying depths (up to ∼200 km) that were transported to the surface in kimberlites and other magmas (Ionov & Wood 1992; Canil et al. 1994; Frost & McCammon 2008). Kasting et al. (1993) briefly review earlier studies that come to essentially the same conclusion—the upper mantle
-bearing mineral assemblages in upper mantle samples (xenoliths) from varying depths (up to ∼200 km) that were transported to the surface in kimberlites and other magmas (Ionov & Wood 1992; Canil et al. 1994; Frost & McCammon 2008). Kasting et al. (1993) briefly review earlier studies that come to essentially the same conclusion—the upper mantle  is near QFM ± a few log units.
is near QFM ± a few log units.
The mantle becomes more reducing with increasing depth (higher pressure) because the ΔV of reactions favors the  –bearing components of garnets at pressures above 3 GPa, which gives lower
–bearing components of garnets at pressures above 3 GPa, which gives lower  values for
values for  –
– mineral buffers at higher pressures. The
mineral buffers at higher pressures. The  at the base of the upper mantle, in the transition zone, and in the lower mantle is 4–5 log units below QFM and Ni–Fe metal alloy is stable. The
at the base of the upper mantle, in the transition zone, and in the lower mantle is 4–5 log units below QFM and Ni–Fe metal alloy is stable. The  of Earth's mantle ranges from IW to IW−1.5 (lower mantle) to QFM ± 2 log units (upper mantle; Frost & McCammon 2008). Figure 9 shows the position of the QFM and IW oxygen fugacity buffers in relation to the calculated
of Earth's mantle ranges from IW to IW−1.5 (lower mantle) to QFM ± 2 log units (upper mantle; Frost & McCammon 2008). Figure 9 shows the position of the QFM and IW oxygen fugacity buffers in relation to the calculated  of individual types of meteoritic material, present-day volcanic gases, and our calculated
of individual types of meteoritic material, present-day volcanic gases, and our calculated  for the bulk silicate Earth from previous work (Fegley & Schaefer 2014). The oxygen fugacities of all the mixtures of meteoritic materials that we studied fall between the end-member values for CI and EH chondritic materials (also shown). The most oxidized mixture is CI chondritic material at about QFM−1, which is within the range of
for the bulk silicate Earth from previous work (Fegley & Schaefer 2014). The oxygen fugacities of all the mixtures of meteoritic materials that we studied fall between the end-member values for CI and EH chondritic materials (also shown). The most oxidized mixture is CI chondritic material at about QFM−1, which is within the range of  values for the upper mantle (shaded gray region). The most reduced mixture is EH chondritic material at ∼IW−1. Metal-free eucrites are about as reduced as EH chondrites, showing that Fe metal is not required for reducing conditions. This point is also illustrated by our prior chemical equilibrium computations of gases formed by heating of H chondritic material with and without metal or FeS (Figures 7 and 8 in Fegley & Schaefer 2014). These calculations show that highly reducing atmospheres are produced from H chondritic material before and after removal of metal and FeS, e.g., during core formation.
values for the upper mantle (shaded gray region). The most reduced mixture is EH chondritic material at ∼IW−1. Metal-free eucrites are about as reduced as EH chondrites, showing that Fe metal is not required for reducing conditions. This point is also illustrated by our prior chemical equilibrium computations of gases formed by heating of H chondritic material with and without metal or FeS (Figures 7 and 8 in Fegley & Schaefer 2014). These calculations show that highly reducing atmospheres are produced from H chondritic material before and after removal of metal and FeS, e.g., during core formation.
Figure 9. Oxygen fugacity of the Bulk Silicate Earth (BSE) compared to standard oxygen fugacity buffers and various measured volcanic gas compositions (Kilauea, convergent and divergent). This figure is reproduced and modified from Fegley & Schaefer (2014). The gray shaded region indicates the observed values from mantle samples of QFM ± 2.
Download figure:
Standard image High-resolution image5.2. Mantle Evolution
The  curves for EH and CI chondritic material quantify the
curves for EH and CI chondritic material quantify the  of the reduced and oxidized end-members in the two-component models of Ringwood (1979) and Wänke for the formation of the Earth (Wänke 1981; Wänke & Dreibus 1982, 1988; Wänke et al. 1984). Their oxidized component is CI chondritic material while their reduced component is as reducing as EH chondritic material but ideally volatile free. They did this for simplicity in the mixing calculations and in reality the reduced component has to contain some volatiles, otherwise redox reactions involving H, C, N, and S could not occur.
of the reduced and oxidized end-members in the two-component models of Ringwood (1979) and Wänke for the formation of the Earth (Wänke 1981; Wänke & Dreibus 1982, 1988; Wänke et al. 1984). Their oxidized component is CI chondritic material while their reduced component is as reducing as EH chondritic material but ideally volatile free. They did this for simplicity in the mixing calculations and in reality the reduced component has to contain some volatiles, otherwise redox reactions involving H, C, N, and S could not occur.
The Ringwood and Wänke two-component models mix 85% of the reduced component and 15% of the oxidized component to form the Earth. Wänke also considers a gradual transition from the reduced to the oxidized component that starts after about 67% of the Earth has accreted (e.g., see p. 9 of Wänke et al. 1984 or pp. 547–548 of Wänke & Dreibus 1988). However, as Figure 4 shows, the  computed from binary mixtures of CI and EH chondritic material is relatively insensitive to the proportion of CI material in the 10%–40% range. So whether we take 85%−15% or 67%−33% for the proportions of reduced and oxidized components is not critical. The
computed from binary mixtures of CI and EH chondritic material is relatively insensitive to the proportion of CI material in the 10%–40% range. So whether we take 85%−15% or 67%−33% for the proportions of reduced and oxidized components is not critical. The  of the two-component mixture (at one bar and 1500 K) is about IW−0.3 log units. The equations in the Appendix are useful for computing the temperature-dependent
of the two-component mixture (at one bar and 1500 K) is about IW−0.3 log units. The equations in the Appendix are useful for computing the temperature-dependent  (at one bar total pressure) of the CI–EH chondritic (or any other) binary mixture that we considered in our work.
(at one bar total pressure) of the CI–EH chondritic (or any other) binary mixture that we considered in our work.
A variety of evidence indicates that the  of the upper mantle has shown relatively little variation with time, at least since 4.35 Gyr ago. This evidence is based on variations of elemental abundances (V, Cr) or elemental ratios (V/Sc) in upper-mantle-derived mafic and ultramafic rocks (Canil 1997, 1999, 2002; Delano 2001; Aulbach & Stagno 2016), the Ce abundance in zircons (Trail et al. 2011; Smythe & Brenan 2016), or the V abundance in olivine and/or chromite in komatiite rocks (Nicklas et al. 2016). All studies conclude that the
of the upper mantle has shown relatively little variation with time, at least since 4.35 Gyr ago. This evidence is based on variations of elemental abundances (V, Cr) or elemental ratios (V/Sc) in upper-mantle-derived mafic and ultramafic rocks (Canil 1997, 1999, 2002; Delano 2001; Aulbach & Stagno 2016), the Ce abundance in zircons (Trail et al. 2011; Smythe & Brenan 2016), or the V abundance in olivine and/or chromite in komatiite rocks (Nicklas et al. 2016). All studies conclude that the  of the upper mantle has been within a few log units of the QFM buffer over time. Typical values (relative to QFM) are ≤−0.3 (Archaean basalts; Li & Lee 2004), ±0.5 (Archaean basalts; Delano 2001), −1.5 to +1.5 (Archaean komatiite; Canil 1997), −1.5 to 0 (cratonic peridotites; Canil 2002), −1.19 ± 0.33 (Aulbach & Stagno 2016), −0.5 ± 2.3 (Hadean zircons; Trail et al. 2011), −1.0 to +2.5 (Hadean zircons; Smythe & Brenan 2016), and finally −0.29 ± 0.04 relative to the Ni–NiO buffer, equivalent to ∼+0.5 log units relative to QFM (Archaean komatiite; Nicklas et al. 2016). (Figure 9 shows that the Ni–NiO buffer is ∼0.8 log units above the QFM line.)
of the upper mantle has been within a few log units of the QFM buffer over time. Typical values (relative to QFM) are ≤−0.3 (Archaean basalts; Li & Lee 2004), ±0.5 (Archaean basalts; Delano 2001), −1.5 to +1.5 (Archaean komatiite; Canil 1997), −1.5 to 0 (cratonic peridotites; Canil 2002), −1.19 ± 0.33 (Aulbach & Stagno 2016), −0.5 ± 2.3 (Hadean zircons; Trail et al. 2011), −1.0 to +2.5 (Hadean zircons; Smythe & Brenan 2016), and finally −0.29 ± 0.04 relative to the Ni–NiO buffer, equivalent to ∼+0.5 log units relative to QFM (Archaean komatiite; Nicklas et al. 2016). (Figure 9 shows that the Ni–NiO buffer is ∼0.8 log units above the QFM line.)
However, there is also evidence that the Earth's mantle experienced a reducing magma ocean state during the time of core formation. During core formation, the silicate portion of the Earth would have been in equilibrium with an Fe–Ni alloy, which would have resulted in an oxygen fugacity of about IW−1 (Frost & McCammon 2008). Trace siderophile element abundances in the mantle are used in models of core formation to try and determine the conditions under which metal−silicate equilibration occurred (e.g., Wade & Wood 2005; Rubie et al. 2011; Righter & Ghiorso 2012). Wade & Wood (2005) require the mantle to increase in oxidation state (FeO content) as the planet grew, and further suggest that the mantle self-oxidizes due to disproportionation of  to
to  in the lower mantle. Rubie et al. (2011) find that during accretion, the oxygen fugacity (FeO content) of the material accreted to the Earth must have been initially reduced and become progressively more oxidized in order to explain the trace element abundances. Numerous later studies agree with this general trend of oxidation during accretion. However, the final oxygen fugacities of these models is generally still too low to explain the Earth's present-day value. For instance, the model of Wade & Wood (2005) uses an increase in
in the lower mantle. Rubie et al. (2011) find that during accretion, the oxygen fugacity (FeO content) of the material accreted to the Earth must have been initially reduced and become progressively more oxidized in order to explain the trace element abundances. Numerous later studies agree with this general trend of oxidation during accretion. However, the final oxygen fugacities of these models is generally still too low to explain the Earth's present-day value. For instance, the model of Wade & Wood (2005) uses an increase in  from IW−4 to IW−2, whereas the highest
from IW−4 to IW−2, whereas the highest  in the Rubie et al. (2011) study is IW−1.9.
in the Rubie et al. (2011) study is IW−1.9.
Therefore, significant oxidation must have occurred since then to account for the present-day  . The apparent constancy of the
. The apparent constancy of the  of the upper mantle over geologic time, at least within the ±2 log unit variability observed for the present-day mantle, implies that dramatic changes (if any) in the oxidation state of the mantle had to take place before the oldest zircons studied by Trail et al. (2011) and Smythe & Brenan (2016) were formed ∼4.35–4.40 Gyr ago. This means sometime within 150–200 million years after the Earth formed ∼4.55 Gyr ago (Patterson 1956; Allègre et al. 1995; Jacobsen et al. 2008). We return to this point in the following section.
of the upper mantle over geologic time, at least within the ±2 log unit variability observed for the present-day mantle, implies that dramatic changes (if any) in the oxidation state of the mantle had to take place before the oldest zircons studied by Trail et al. (2011) and Smythe & Brenan (2016) were formed ∼4.35–4.40 Gyr ago. This means sometime within 150–200 million years after the Earth formed ∼4.55 Gyr ago (Patterson 1956; Allègre et al. 1995; Jacobsen et al. 2008). We return to this point in the following section.
Kasting et al. (1993) discuss four possible methods to oxidize the Earth's mantle to its present-day state: (1) reaction of ferrous iron in the mantle with water after metal segregation to produce small amounts of ferric iron, (2) disproportionation of ferrous iron to ferric iron and metal in the lower mantle and later homogenization of the mantle through convection, (3) late accretion of oxidized material following core formation and escape of hydrogen gas, and (4) slow oxidation through volatile recycling into the mantle and loss of hydrogen gas. Sharp et al. (2013) and Hamano et al. (2013) also suggest that escape of hydrogen from the atmosphere during the early magma ocean stages could result in oxidation of the mantle. We return to hydrogen escape in the next section. However, we note that the CI–CV–eucrite ternary mixture is then suggestive of Kasting's third possible oxidation mechanism. The relatively reduced eucrite is representative of a differentiated silicate, the residue of a mantle after core segregation. The addition of only small amounts of oxidized material (here the CI or CV chondritic material) has a controlling influence on the  of the mixture. For CI–eucritic binaries, only 2% to 3% of CI material is needed to raise the
of the mixture. For CI–eucritic binaries, only 2% to 3% of CI material is needed to raise the  2.5 log units. Although CI material is not quite oxidized enough to explain the upper mantle, loss of hydrogen could have further increased the
2.5 log units. Although CI material is not quite oxidized enough to explain the upper mantle, loss of hydrogen could have further increased the  as we discuss below. So, the addition of a small amount of carbonaceous material to the mantle after core formation as suggested in the late veneer model plus slight oxidation through outgassing may have been sufficient to produce the present-day mantle oxidation state.
as we discuss below. So, the addition of a small amount of carbonaceous material to the mantle after core formation as suggested in the late veneer model plus slight oxidation through outgassing may have been sufficient to produce the present-day mantle oxidation state.
6. Hydrogen Degassing and Escape
6.1. Degassing
Studies of degassing of volatiles from magmas have shown that the oxygen fugacity of a volcanic gas is typically not the same as the parent lava, which may also have a different oxidation state than the parent magma (e.g., Mathez 1984; Burgisser & Scaillet 2007; Humphreys et al. 2015). Humphreys et al. (2015) have shown that degassing experiments produce an increase in the  /ΣFe with decreasing
/ΣFe with decreasing  concentration, due to loss of
concentration, due to loss of  into bubbles during decompression. That is, as a lava degasses and loses H, it should become more oxidized. Mathez (1984), however, showed that as the
into bubbles during decompression. That is, as a lava degasses and loses H, it should become more oxidized. Mathez (1984), however, showed that as the  of a system increases, the reaction
of a system increases, the reaction
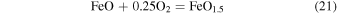
exerts a greater buffering influence on the system. Therefore, for reduced compositions with  near IW, the degassing of the lava changes the
near IW, the degassing of the lava changes the  very little, whereas degassing hydrogen gas from lavas that are originally more oxidized may have a stronger effect on increasing the
very little, whereas degassing hydrogen gas from lavas that are originally more oxidized may have a stronger effect on increasing the  . As described by Kasting et al. (1993) and Sharp et al. (2013), net oxidation of the planet can occur if the outgassed hydrogen escapes from the atmosphere.
. As described by Kasting et al. (1993) and Sharp et al. (2013), net oxidation of the planet can occur if the outgassed hydrogen escapes from the atmosphere.
As a quick test of the degree to which hydrogen loss would affect the oxidation state of our calculated atmospheres, we recompute the binary mixtures of the reduced components (H, EH, and eucrite) with CI chondritic material with lower total hydrogen abundances (50% and 10% of initial values). Results are shown in Figure 10 compared to the nominal calculations from Figure 4. The figure shows that the loss of H has a much larger effect on the oxidized CI chondritic material than on the reduced materials, as we had supposed. This is likely due to both the initial source of hydrogen in these materials and the presence of buffering phases in the reduced materials. Hydrogen in the CI chondritic material is mostly in the form of bound water, whereas in EH chondritic material, much of the hydrogen is bound in insoluble organic material (Robert 2003). Therefore, loss of hydrogen from carbonaceous materials frees up oxygen, whereas loss of hydrogen from EH chondritic material does not. Although some of the hydrogen in ordinary chondrites is in the form of bound water, there are also buffering phases in both the EH and H chondritic materials (metal and reduced carbon). As noted in Sharp et al. (2013), loss of hydrogen gas will not raise the oxygen fugacity until the buffering phases have been fully oxidized. We note that hydrogen loss from the binary of the CI chondritic material with the differentiated eucritic material produces strong oxidation across the binary range. The differentiated eucrite has small volatile abundances and no strongly buffering mineral components, which is why the binary becomes strongly oxidized by the loss of H.
Figure 10. Oxygen fugacity of binaries of reduced materials with CI chondritic material with either 50% (blue lines) or 10% (red lines) of the initial hydrogen abundance compared to the nominal compositions (black lines). (Left) CI–EH binary, (center) CI–H binary, and (right) CI–eucrite binary. All calculations are at 1500 K and 1 bar total pressure.
Download figure:
Standard image High-resolution image6.2. Atmospheric Escape
The importance of atmospheric escape has been known for decades but the exact effects on atmospheric composition are still debated vigorously. The hydrogen escape rate from the primordial Earth is difficult to constrain because it depends on whether or not escape is diffusion limited (as it is today due to the high exospheric temperature >1000 K) or energy limited (as it would be for lower exospheric temperatures such as those in the  -rich atmospheres of Venus and Mars, and possibly in an early anoxic atmosphere on the early Earth). The difference may be large—Tian et al. (2005) compute a 100× smaller
-rich atmospheres of Venus and Mars, and possibly in an early anoxic atmosphere on the early Earth). The difference may be large—Tian et al. (2005) compute a 100× smaller  escape rate on early Earth—but their result is controversial (e.g., see the discussion in Catling 2006; Kuramoto et al. 2013; Tian 2015). For instance, Kuramoto et al. (2013) found H escape rates a few to a few tens of times larger than Tian et al. (2005) using a more sophisticated numerical scheme. Also, it is possible that hydrodynamic escape occurred, either while the early Sun had an enhanced extreme UV (EUV) flux or perhaps driven by the Moon-forming impact.
escape rate on early Earth—but their result is controversial (e.g., see the discussion in Catling 2006; Kuramoto et al. 2013; Tian 2015). For instance, Kuramoto et al. (2013) found H escape rates a few to a few tens of times larger than Tian et al. (2005) using a more sophisticated numerical scheme. Also, it is possible that hydrodynamic escape occurred, either while the early Sun had an enhanced extreme UV (EUV) flux or perhaps driven by the Moon-forming impact.
The current hydrogen escape rate from the Earth is 3 × 108 H atoms cm−2 s−1, which is ∼4 × 1010 moles  per year. This is diffusion limited and depends on the total
per year. This is diffusion limited and depends on the total  mixing ratio at the homopause, above which diffusive separation of gases occurs (Hunten & Donahue 1976). To first approximation, the
mixing ratio at the homopause, above which diffusive separation of gases occurs (Hunten & Donahue 1976). To first approximation, the  escape rate (ϕ) from Earth's atmosphere is
escape rate (ϕ) from Earth's atmosphere is  , where fT is the total mixing ratio of
, where fT is the total mixing ratio of  -bearing species at the homopause (∼6 parts per million by volume (ppmv) in Earth's atmosphere).
-bearing species at the homopause (∼6 parts per million by volume (ppmv) in Earth's atmosphere).
Following Walker (1982), we now consider hydrogen escape from a primordial Earth with its composition given by the two-component models of Ringwood and Wänke. In both models, the Earth is made from 15% CI chondritic material, which contains ∼2% hydrogen (see Table 1), so the total H added is ( kg)(0.15)(0.01973) =
kg)(0.15)(0.01973) =  kg =
kg =  moles H. Palme & O'Neill (2014) give ∼120 μg g−1 H in the BSE, and assuming no additional H in the core, Earth's current H inventory is 4.84 × 1020 kg (4.80 × 1023 moles). This is about 3% of the amount initially added by the two-component models. Walker (1982) computed a similar number by considering only water in Earth's oceans. The removal of the "excess" 1.72 × 1022 kg (1.71 × 1025 moles) H requires a hydrogen escape rate significantly greater than the current value. Taking at face value the indicators of mantle
moles H. Palme & O'Neill (2014) give ∼120 μg g−1 H in the BSE, and assuming no additional H in the core, Earth's current H inventory is 4.84 × 1020 kg (4.80 × 1023 moles). This is about 3% of the amount initially added by the two-component models. Walker (1982) computed a similar number by considering only water in Earth's oceans. The removal of the "excess" 1.72 × 1022 kg (1.71 × 1025 moles) H requires a hydrogen escape rate significantly greater than the current value. Taking at face value the indicators of mantle  over time, the excess H has to be removed within 150–200 million years of Earth's formation. This requires H escape rates of (0.85–1.14) × 1017 moles per year, about 2.1–2.8 million times faster than at present. We have not attempted to model the hydrodynamic escape of hydrogen from the early Earth because this is beyond the scope of this paper, but this value may be close to the upper limit of the possible escape rate for the Earth from impinging solar EUV radiation. Two alternative scenarios are possible to explain any excess early hydrogen escape. The first is that the Moon-forming impact removed the excess hydrogen from the early Earth but the amount of atmosphere lost in a big impact is model dependent and varies from 10% in the absence of oceans (Genda & Abe 2003) to 99% in the presence of oceans (Genda & Abe 2005). Schlichting et al. (2015) have also shown that the balance between impact erosion and addition to the atmosphere by impact degassing depends sensitively on the size distribution of impactors and their volatile contents. Pepin (1997) considered hydrodynamic escape driven by the thermal energy of the Moon-forming impact but focused on the implications for noble gases. The implications for hydrogen loss and D/H fractionation were not explored. Clearly, more work is needed to answer this question. Even if the Moon-forming impact caused extensive hydrogen loss on Earth, it is doubtful this mechanism affected all rocky planets with atmospheres. The second alternative is that the large required H escape rate may be a sign that the oldest indicators of mantle
over time, the excess H has to be removed within 150–200 million years of Earth's formation. This requires H escape rates of (0.85–1.14) × 1017 moles per year, about 2.1–2.8 million times faster than at present. We have not attempted to model the hydrodynamic escape of hydrogen from the early Earth because this is beyond the scope of this paper, but this value may be close to the upper limit of the possible escape rate for the Earth from impinging solar EUV radiation. Two alternative scenarios are possible to explain any excess early hydrogen escape. The first is that the Moon-forming impact removed the excess hydrogen from the early Earth but the amount of atmosphere lost in a big impact is model dependent and varies from 10% in the absence of oceans (Genda & Abe 2003) to 99% in the presence of oceans (Genda & Abe 2005). Schlichting et al. (2015) have also shown that the balance between impact erosion and addition to the atmosphere by impact degassing depends sensitively on the size distribution of impactors and their volatile contents. Pepin (1997) considered hydrodynamic escape driven by the thermal energy of the Moon-forming impact but focused on the implications for noble gases. The implications for hydrogen loss and D/H fractionation were not explored. Clearly, more work is needed to answer this question. Even if the Moon-forming impact caused extensive hydrogen loss on Earth, it is doubtful this mechanism affected all rocky planets with atmospheres. The second alternative is that the large required H escape rate may be a sign that the oldest indicators of mantle  may be compromised and/or non-unique and that reducing conditions existed for a much longer time.
may be compromised and/or non-unique and that reducing conditions existed for a much longer time.
Hamano et al. (2013) modeled magma ocean evolution with a steam atmosphere for planets at different orbital distances from the Sun. In their model, dissociation of steam in the atmosphere followed by hydrogen escape produced free oxygen, which they assumed was absorbed into the magma ocean. At the Earth's orbit, the authors determined that the amount of oxygen absorbed could have increased the  abundance in the mantle by 0.07 wt%. However, their model assumed a pure steam atmosphere, whereas the magma ocean following the giant Moon-forming impact and associated with core formation should have been reduced, with an oxygen fugacity below IW as previously discussed. The atmosphere would therefore have been dominated by
abundance in the mantle by 0.07 wt%. However, their model assumed a pure steam atmosphere, whereas the magma ocean following the giant Moon-forming impact and associated with core formation should have been reduced, with an oxygen fugacity below IW as previously discussed. The atmosphere would therefore have been dominated by  gas rather than steam, and so their model may underestimate the amount of hydrogen lost.
gas rather than steam, and so their model may underestimate the amount of hydrogen lost.
6.3. Venus and Mars
Venus has ∼270,000 times less observable hydrogen than the Earth. The 30 ppm  in the Venusian atmosphere corresponds to a column density of ∼1 g cm−2 versus ∼270,000 g cm−2 water in Earth's oceans. The deuterium (D) to hydrogen (H) atomic ratio in Venusian water vapor is 0.025 ± 0.005, which is about 160 ± 32 times larger than the terrestrial D/H ratio of 1.558 × 10−4 in standard mean ocean water. Venus' water deficit and high D/H ratio are generally ascribed to massive hydrogen escape (Donahue et al. 1997). The mean FeO/MnO ratio of Venus' surface from Venera 13, 14, and Vega 2 measurements is ∼52 (Surkov et al. 1984, 1986; Volkov et al. 1986), only slightly less than that of the bulk silicate Earth (∼60). The FeO/MnO ratio depends strongly on a planet's oxidation state (Wänke et al. 1973). The values for Earth and Venus fall into an orderly sequence (from the most oxidizing to most reducing): CI chondrites 96, angrites 88, Earth 60, Venus 52, Mars (SNC parent body) 40, Vesta (eucrite parent body) 34, and mesosiderites 24. Thus, massive loss of hydrogen from Venus has not dramatically oxidized its silicate portion more than that of the Earth. The absence of any detectable
in the Venusian atmosphere corresponds to a column density of ∼1 g cm−2 versus ∼270,000 g cm−2 water in Earth's oceans. The deuterium (D) to hydrogen (H) atomic ratio in Venusian water vapor is 0.025 ± 0.005, which is about 160 ± 32 times larger than the terrestrial D/H ratio of 1.558 × 10−4 in standard mean ocean water. Venus' water deficit and high D/H ratio are generally ascribed to massive hydrogen escape (Donahue et al. 1997). The mean FeO/MnO ratio of Venus' surface from Venera 13, 14, and Vega 2 measurements is ∼52 (Surkov et al. 1984, 1986; Volkov et al. 1986), only slightly less than that of the bulk silicate Earth (∼60). The FeO/MnO ratio depends strongly on a planet's oxidation state (Wänke et al. 1973). The values for Earth and Venus fall into an orderly sequence (from the most oxidizing to most reducing): CI chondrites 96, angrites 88, Earth 60, Venus 52, Mars (SNC parent body) 40, Vesta (eucrite parent body) 34, and mesosiderites 24. Thus, massive loss of hydrogen from Venus has not dramatically oxidized its silicate portion more than that of the Earth. The absence of any detectable  and
and  in Venus' atmosphere and the presence of
in Venus' atmosphere and the presence of  , OCS, and sulfur vapor argue for volcanic degassing at oxygen fugacity values in the range of the QFM and Ni-NiO buffers like the Earth.
, OCS, and sulfur vapor argue for volcanic degassing at oxygen fugacity values in the range of the QFM and Ni-NiO buffers like the Earth.
Mars has a FeO/MnO ratio of 40 (from SNC meteorites; Wänke & Dreibus 1988), which is lower (i.e., more reducing) than that of the Earth. Wadhwa (2008) reviews the indirect  determinations of SNC meteorites, which have
determinations of SNC meteorites, which have  ranging from IW−1 to IW+4. The correlation of the
ranging from IW−1 to IW+4. The correlation of the  values with other geochemical and isotopic data indicates the Martian mantle
values with other geochemical and isotopic data indicates the Martian mantle  is about that of the IW buffer. However, Mars has undergone extensive hydrogen escape to elevate the D/H ratio of atmospheric water vapor to ∼5 times the terrestrial D/H ratio (Owen et al. 1988; Yung et al. 1988; Donahue 1995; Krasnopolsky et al. 1997; Krasnopolsky 2015).
is about that of the IW buffer. However, Mars has undergone extensive hydrogen escape to elevate the D/H ratio of atmospheric water vapor to ∼5 times the terrestrial D/H ratio (Owen et al. 1988; Yung et al. 1988; Donahue 1995; Krasnopolsky et al. 1997; Krasnopolsky 2015).
Thus, Venus and Mars have likely lost large amounts of hydrogen at some time in the past yet neither of them are significantly more oxidized than the Earth. The volatile recycling model of Kasting et al. (1993) and the hydrogen escape during the magma ocean phase of Hamano et al. (2013) and Sharp et al. (2013) both require sufficient initial volatile abundances to oxidize any mineral buffers. The volatiles must also at some time be sequestered in the mantle to have this oxidizing effect. The lack of oxidation of Mars and Venus suggests that possibly one of these conditions was not met (insufficient volatiles, no recycling of volatiles into the mantle) on these planets. Whatever the truth, the effects of hydrogen escape on the redox state of bulk silicate planets are extremely complicated and require additional studies.
6.4. Exoplanet Atmospheres
An important issue is the very large escape rates required to remove excess hydrogen from rocky planets formed by the accretion of volatile-rich chondritic material. Planets at close orbital separations and planets around M dwarfs are likely subjected to much higher energetic radiation environments than the Earth. Studies by Luger & Barnes (2015), Schaefer et al. (2016), and Barnes et al. (2016), to name a few, have looked at models similar to those of Hamano et al. (2013) for hydrogen loss and oxygen build-up on rocky exoplanets during a magma ocean phase. Schaefer et al. (2016) showed that oxygen absorption into the magma ocean is not complete, and that the amount of oxygen absorbed is a balance between the rate of oxygen escape and the rate of solidification of the magma ocean. The results of these studies show that planets farther out in orbital space are less likely to lose significant amounts of hydrogen. Zahnle & Catling (2017) also consider the question of atmospheric escape due to both stellar radiation as well as impacts. They present figures showing a large number of exoplanets that fall into their region of atmospheric stability, suggesting that hydrogen escape may be less important for some rocky exoplanets.
7. Summary
In this paper, we present calculations of the oxygen fugacity of atmospheres produced by the outgassing of mixtures of primitive solar nebular materials, which we approximate with meteoritic materials. Our calculations are generally applicable to both impact degassed and outgassed atmospheres. We used materials with a range of initial oxidation states from highly oxidized (carbonaceous chondritic material) to highly reduced (enstatite chondritic or eucritic materials). We show that when the solid materials equilibrate as would be expected through intimate mixing during accretion, the gases produced are not a straightforward linear mixture of the gases produced by the individual materials. This is likely due to the presence of buffering phases such as metallic iron within the solid material. As such, calculations of each mixture of interest are necessary to accurately produce the  of the system.
of the system.
Differentiated primitive materials such as eucritic material have markedly less effect on binary and ternary diagrams with the highly oxidized carbonaceous materials than either the ordinary or enstatite chondritic materials did, despite having a similar low  . This may be due to either the low volatile abundance of the eucritic material or low amounts of metallic iron. Addition of only a few percent of carbonaceous material to a differentiated body may be sufficient to raise the
. This may be due to either the low volatile abundance of the eucritic material or low amounts of metallic iron. Addition of only a few percent of carbonaceous material to a differentiated body may be sufficient to raise the  of the mixture by several log units. Future work should explore the behavior of other differentiated or primitive achondrites in mixtures. For instance, aubrites, which are more reduced than eucrites, and angrites, which are more oxidized, may exhibit different behaviors in mixtures. Comparing other achondritic materials with the eucritic calculations presented here may shed light on redox processes within differentiated planetesimals.
of the mixture by several log units. Future work should explore the behavior of other differentiated or primitive achondrites in mixtures. For instance, aubrites, which are more reduced than eucrites, and angrites, which are more oxidized, may exhibit different behaviors in mixtures. Comparing other achondritic materials with the eucritic calculations presented here may shed light on redox processes within differentiated planetesimals.
We also provide polynomial fits to the oxygen fugacities for the individual materials and the binary mixtures. These will have applications to the modeling of the formation of atmospheres during the accretion of the rocky solar system planets including the Earth, Mars, and Venus, as well as exoplanetary atmospheres. The calculated oxygen fugacities will be useful in models of core formation, particularly in meteorite parent bodies or other planetesimals since trace element partitioning behavior is often dependent on the oxidation state of the system.
We acknowledge that hydrogen escape, photochemistry, surface–atmosphere interactions, and a whole host of other processes are likely to alter the oxygen fugacity of any rocky planet's atmosphere. However, these calculations provide a simplified jumping-off point for future models of atmospheric formation and evolution from natural starting materials. Our initial calculations, allowing for atmospheric equilibration with the solid material, indicate that oxidized materials become more oxidized by hydrogen loss, whereas reduced materials do not. More detailed calculations of how these processes determine the evolution of the atmospheric oxidation state and the degree to which atmospheric oxygen fugacity can affect mantle oxidation state are needed.
L.S. acknowledges funding from the Simons Foundation, the Harvard-Smithsonian Center for Astrophysics, and Arizona State University. B.F. was supported by NSF Astronomy Program Grants AST-1412175 and AST-1517541. The authors would like to thank an anonymous reviewer for helpful comments.
Appendix: Fits to Binary Mixtures of Meteoritic Material
We provide fits to the oxygen fugacities of all of the binary mixtures as a function of temperature in Table 3. The fits are tabulated at every 10% step in composition. These fits may be useful in parameterized models of planet formation, which track composition and volatile outgassing, or for use with trace element partitioning studies. Tables of values for the ternary mixtures are available from the first author upon request.
Table 3.
Oxygen Fugacity Fits for Binary Mixtures of Meteoritic Materials as a Function of Temperature (log10  = a +
= a +  /T +
/T +  /T2 +
/T2 +  /T3 +
/T3 +  /T4) at 1 bar Total Pressure
/T4) at 1 bar Total Pressure
| a | b | c | d | f | r2 | |
|---|---|---|---|---|---|---|
| XCI | CI–CV | |||||
| 0.1 | 8.0651 | −28.8522 | 4.0408 | −1.9772 | 0.2558 | 0.9996 |
| 0.2 | 7.3792 | −25.5407 | −1.3133 | 1.2397 | −0.2787 | 0.9996 |
| 0.3 | 8.1118 | −28.3287 | 2.1094 | −0.3605 | −0.0039 | 0.9995 |
| 0.4 | 6.2640 | −21.8893 | −5.2874 | 3.0056 | −0.4954 | 0.9997 |
| 0.5 | 3.1031 | −11.2876 | −16.7472 | 7.8460 | −1.1632 | 0.9998 |
| 0.6 | 3.6070 | −13.1228 | −14.4758 | 6.8306 | −1.0180 | 0.9998 |
| 0.7 | 2.5364 | −9.6142 | −18.0889 | 8.2716 | −1.2003 | 0.9998 |
| 0.8 | 2.8901 | −11.0920 | −15.9412 | 7.0870 | −0.9815 | 0.9998 |
| 0.9 | 2.6228 | −10.2397 | −16.7573 | 7.4100 | −1.0258 | 0.9998 |
| XCI | CI–H | |||||
| 0.1 | 5.0058 | −22.6589 | −5.9180 | 2.1646 | −0.2752 | 0.9999 |
| 0.2 | 4.8543 | −22.5311 | −5.5893 | 1.9003 | −0.2272 | 0.9999 |
| 0.3 | 13.358 | −52.6189 | 27.8179 | −10.9516 | 1.3864 | 0.9997 |
| 0.4 | 13.158 | −51.8691 | 28.3404 | −11.5132 | 1.4933 | 0.9997 |
| 0.5 | 11.991 | −44.1493 | 17.5291 | −6.0115 | 0.7015 | 0.9997 |
| 0.6 | 8.7138 | −31.2625 | 2.8127 | 0.4223 | −0.2042 | 0.9998 |
| 0.7 | 7.1908 | −25.1986 | −3.7546 | 3.1928 | −0.5971 | 0.9998 |
| 0.8 | 5.9230 | −20.7534 | −7.8992 | 4.6609 | −0.7622 | 0.9998 |
| 0.9 | 4.7183 | −16.9602 | −10.6833 | 5.2643 | −0.7649 | 0.9998 |
| XCI | CI–EH | |||||
| 0.1 | 3.8832 | −20.5812 | −6.8240 | 2.1862 | −0.2473 | 0.9999 |
| 0.2 | 3.6947 | −19.4138 | −8.4046 | 2.9421 | −0.3598 | 0.9999 |
| 0.3 | 6.6457 | −29.1113 | 2.4778 | −1.5776 | 0.2553 | 0.9999 |
| 0.4 | 14.4638 | −56.3141 | 32.0861 | −12.7445 | 1.6370 | 0.9996 |
| 0.5 | 11.1056 | −42.8672 | 16.0666 | −5.3600 | 0.6091 | 0.9998 |
| 0.6 | 9.6609 | −35.9264 | 7.7951 | −1.5696 | 0.0640 | 0.9998 |
| 0.7 | 8.0690 | −29.0678 | 0.2449 | 1.6147 | −0.3841 | 0.9998 |
| 0.8 | 6.9125 | −24.3452 | −4.4232 | 3.3853 | −0.6128 | 0.9998 |
| 0.9 | 5.1947 | −18.7155 | −9.1692 | 4.7989 | −0.7237 | 0.9998 |
| XCI | CI–Euc | |||||
| 0.1 | 9.0439 | −32.8601 | 6.8006 | −2.0526 | 0.1799 | 0.9996 |
| 0.2 | 7.9465 | −28.9356 | 3.3216 | −0.8340 | 0.0300 | 0.9995 |
| 0.3 | 4.4434 | −16.6391 | −10.3866 | 5.0634 | −0.7694 | 0.9997 |
| 0.4 | 3.9235 | −14.8792 | −12.1100 | 5.7424 | −0.8611 | 0.9997 |
| 0.5 | 3.6859 | −14.0380 | −12.9252 | 6.0625 | −0.9047 | 0.9997 |
| 0.6 | 3.5317 | −13.4420 | −13.5247 | 6.3008 | −0.9371 | 0.9997 |
| 0.7 | 2.3658 | −9.5124 | −17.7374 | 8.0329 | −1.1720 | 0.9998 |
| 0.8 | 2.4815 | −10.0685 | −16.7976 | 7.4508 | −1.0581 | 0.9997 |
| 0.9 | 2.3497 | −9.6931 | −17.0402 | 7.4372 | −1.0204 | 0.9998 |
| XCV | CV–H | |||||
| 0.1 | 5.2129 | −23.6888 | −4.4242 | 1.4579 | −0.1708 | 0.9999 |
| 0.2 | 4.7221 | −21.6215 | −6.7461 | 2.4321 | −0.3048 | 0.9999 |
| 0.3 | 4.7181 | −21.6040 | −6.7657 | 2.4401 | −0.3059 | 0.9999 |
| 0.4 | 4.7181 | −21.6040 | −6.7657 | 2.4401 | −0.3059 | 0.9999 |
| 0.5 | 4.7181 | −21.6040 | −6.7657 | 2.4401 | −0.3059 | 0.9999 |
| 0.6 | 4.4981 | −21.0292 | −7.1782 | 2.5509 | −0.3157 | 0.9999 |
| 0.7 | 4.4208 | −21.3401 | −6.1417 | 1.9415 | −0.2168 | 0.9999 |
| 0.8 | 3.7726 | −18.9490 | −8.0850 | 2.5858 | −0.2916 | 0.9999 |
| 0.9 | 9.8631 | −39.1863 | 14.3754 | −6.2934 | 0.8741 | 0.9997 |
| XCV | CV–EH | |||||
| 0.1 | 3.7982 | −20.2424 | −7.5967 | 2.6627 | −0.3321 | 0.9999 |
| 0.2 | 3.6943 | −19.2932 | −8.7403 | 3.1223 | −0.3890 | 0.9999 |
| 0.3 | 4.9701 | −22.8836 | −5.2751 | 1.7952 | −0.2158 | 0.9999 |
| 0.4 | 5.0795 | −23.1937 | −5.0329 | 1.7478 | −0.2140 | 0.9999 |
| 0.5 | 4.7852 | −21.8459 | −6.5161 | 2.3425 | −0.2931 | 0.9999 |
| 0.6 | 4.7181 | −21.6040 | −6.7657 | 2.4401 | −0.3059 | 0.9999 |
| 0.7 | 4.4303 | −20.9334 | −7.1190 | 2.4824 | −0.3024 | 0.9999 |
| 0.8 | 4.5780 | −21.6615 | −6.0492 | 1.9767 | −0.2284 | 0.9999 |
| 0.9 | 4.7412 | −21.9000 | −4.5036 | 1.0585 | −0.0802 | 0.9998 |
| XCV | CV–euc | |||||
| 0.1 | 3.9199 | −20.4273 | −6.7599 | 2.1509 | −0.2538 | 0.9999 |
| 0.2 | 9.0700 | −37.8667 | 13.7802 | −6.5119 | 0.9368 | 0.9998 |
| 0.3 | 9.1056 | −36.0463 | 11.4341 | −5.3842 | 0.7799 | 0.9996 |
| 0.4 | 7.6575 | −28.7477 | 2.6209 | −1.5476 | 0.2363 | 0.9999 |
| 0.5 | 12.157 | −41.7744 | 15.1001 | −5.4811 | 0.6723 | 0.9993 |
| 0.6 | 12.674 | −43.3422 | 16.7428 | −6.0804 | 0.7216 | 0.9993 |
| 0.7 | 12.413 | −42.6479 | 16.2381 | −5.9424 | 0.7090 | 0.9994 |
| 0.8 | 11.289 | −39.2262 | 13.1691 | −4.8678 | 0.5795 | 0.9995 |
| 0.9 | 9.8200 | −34.7301 | 9.1088 | −3.4361 | 0.4058 | 0.9995 |
| XH | H–EH | |||||
| 0.1 | 4.6347 | −22.8091 | −5.5258 | 1.9611 | −0.2540 | 0.9999 |
| 0.2 | 4.0779 | −20.9356 | −6.9967 | 2.4464 | −0.3044 | 0.9999 |
| 0.3 | 2.6832 | −15.4431 | −13.642 | 5.5494 | −0.7915 | 0.9999 |
| 0.4 | 3.9424 | −19.9489 | −8.2592 | 2.9886 | −0.3765 | 0.9999 |
| 0.5 | 4.6621 | −21.8667 | −6.5473 | 2.3713 | −0.2993 | 0.9999 |
| 0.6 | 5.1021 | −22.9954 | −5.5663 | 2.0239 | −0.2564 | 0.9999 |
| 0.7 | 5.0994 | −22.9862 | −5.5759 | 2.0276 | −0.2568 | 0.9999 |
| 0.8 | 5.1047 | −23.0103 | −5.5391 | 2.0051 | −0.2522 | 0.9999 |
| 0.9 | 5.1047 | −23.0103 | −5.5391 | 2.0051 | −0.2522 | 0.9999 |
| XH | H–Euc | |||||
| 0.1 | 5.4856 | −25.1270 | −3.6580 | 1.3014 | −0.1650 | 0.9999 |
| 0.2 | 2.9707 | −17.2322 | −10.7929 | 3.8186 | −0.4711 | 0.9999 |
| 0.3 | 2.9024 | −16.9680 | −11.1345 | 3.9897 | −0.4983 | 0.9999 |
| 0.4 | 2.9190 | −17.0384 | −11.0318 | 3.9293 | −0.4861 | 0.9999 |
| 0.5 | 4.0032 | −20.3909 | −7.4060 | 2.4414 | −0.2841 | 0.9999 |
| 0.6 | 4.3384 | −21.4308 | −6.4199 | 2.1137 | −0.2494 | 0.9999 |
| 0.7 | 5.5092 | −24.5053 | −3.7107 | 1.1500 | −0.1304 | 0.9999 |
| 0.8 | 5.1047 | −23.0103 | −5.5391 | 2.0051 | −0.2522 | 0.9999 |
| 0.9 | 5.1047 | −23.0103 | −5.5391 | 2.0051 | −0.2522 | 0.9999 |
| XEH | EH–Euc | |||||
| 0.1 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.2 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.3 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.4 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.5 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.6 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.7 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.8 | 5.4856 | −25.1271 | −3.6579 | 1.3014 | −0.1650 | 0.9999 |
| 0.9 | 5.7411 | −25.9808 | −2.7678 | 0.9720 | −0.1253 | 0.9999 |
Note. Fits are computed for temperatures from 300 to 2000 K.
Footnotes
- 4
Oxygen fugacity is the partial pressure of
 gas in equilibrium with a mineral assemblage, corrected for non-ideality.
gas in equilibrium with a mineral assemblage, corrected for non-ideality.