RMSEA, CFI, and TLI in structural equation modeling with ordered categorical data: The story they tell depends on the estimation methods

Abstract

In structural equation modeling, application of the root mean square error of approximation (RMSEA), comparative fit index (CFI), and Tucker–Lewis index (TLI) highly relies on the conventional cutoff values developed under normal-theory maximum likelihood (ML) with continuous data. For ordered categorical data, unweighted least squares (ULS) and diagonally weighted least squares (DWLS) based on polychoric correlation matrices have been recommended in previous studies. Although no clear suggestions exist regarding the application of these fit indices when analyzing ordered categorical variables, practitioners are still tempted to adopt the conventional cutoff rules. The purpose of our research was to answer the question: Given a population polychoric correlation matrix and a hypothesized model, if ML results in a specific RMSEA value (e.g., .08), what is the RMSEA value when ULS or DWLS is applied? CFI and TLI were investigated in the same fashion. Both simulated and empirical polychoric correlation matrices with various degrees of model misspecification were employed to address the above question. The results showed that DWLS and ULS lead to smaller RMSEA and larger CFI and TLI values than does ML for all manipulated conditions, regardless of whether or not the indices are scaled. Applying the conventional cutoffs to DWLS and ULS, therefore, has a pronounced tendency not to discover model–data misfit. Discussions regarding the use of RMSEA, CFI, and TLI for ordered categorical data are given.

“Does the hypothesized model fit the data well?” This is a critical question in almost every application of structural equation modeling (SEM). The model chi-square statistic and several fit indices are commonly reported to address this question. Three model fit indices that are widely applied are considered in this article, all of which are based on a fit function given a specific estimation method. They are the root mean square error of approximation (RMSEA; Steiger, 1990; Steiger & Lind, 1980), comparative fit index (CFI; Bentler, 1990), and Tucker–Lewis index (TLI; Bentler & Bonett, 1980; Tucker & Lewis, 1973). RMSEA is an absolute fit index, in that it assesses how far a hypothesized model is from a perfect model. On the contrary, CFI and TLI are incremental fit indices that compare the fit of a hypothesized model with that of a baseline model (i.e., a model with the worst fit).

The application of RMSEA, CFI, and TLI is heavily contingent on a set of cutoff criteria. Earlier research (e.g., Browne & Cudeck, 1993; Jöreskog & Sörbom, 1993) suggested that an RMSEA value of < .05 indicates a “close fit,” and that < .08 suggests a reasonable model–data fit. Bentler and Bonett (1980) recommended that TLI > .90 indicates an acceptable fit. However, these suggestions are largely based on intuition and experience rather than on any statistical justification (see Marsh, Hau, & Wen, 2004). To address the lack of statistical justification of these recommendations, Hu and Bentler (1999) conducted a simulation study to investigate the rejection rates under correct and misspecified models, by applying various cutoff values for many fit indices, including RMSEA, CFI, and TLI. Hu and Bentler suggested that an RMSEA smaller than .06 and a CFI and TLI larger than .95 indicate relatively good model–data fit in general. Hu and Bentler’s study has become highly influential, and their recommended cutoffs have been adopted in many SEM practices. However, Hu and Bentler’s study only concerns continuous data that are analyzed using the normal-theory maximum likelihood (ML). Hu and Bentler cautioned that the suggested cutoff values might not generalize to conditions that were not manipulated in their study, nor to estimation methods other than ML.

In psychological research the data are frequently ordered categorical (e.g., data collected using Likert scales). Applying the normal-theory ML to the covariance matrix of ordered categorical data can result in biased parameter estimates, inaccurate standard errors, and a misleading chi-square statistic, especially when the number of categories is below five and the categorical distribution is highly asymmetric (e.g., Beauducel & Herzberg, 2006; Johnson & Creech, 1983; Rhemtulla, Brosseau-Liard, & Savalei, 2012). To address the categorical nature of data, the diagonally weighted least squares (DWLS) estimator based on the polychoric correlation matrix has become the most popular method (Savalei & Rhemtulla, 2013). Mplus (L. K. Muthén & Muthén, 2015) by default implements DWLS when variables are specified as being categorical, with mean- and variance-adjusted chi-square statistics and standard errors. (DWLS with such robust corrections is termed mean- and variance-adjusted weighted least squares—i.e., WLSMV; B. O. Muthén, du Toit, & Spisic, 1997.)

RMSEA, CFI, and TLI are based on a fit function that is specific to a chosen estimation method. Because the chi-square statistic is a function of the fit function, RMSEA, CFI, and TLI are also functions of the chi-square statistic. When the scaled chi-square statistic is used in calculating the DWLS fit indices (e.g., Mplus and lavaan in R; see Eqs. 8–10), we denote the resulting fit indices as scaled fit indices—that is, RMSEA_S, CFI_S, and TLI_S. Although the scaled fit indices are widely applied, no theoretical justification exists for the use of robust chi-square in calculating the fit indices (Brosseau-Liard & Savalei, 2014; Brosseau-Liard, Savalei, & Li, 2012). When the fit indices are calculated as functions of the unscaled chi-square statistic, we denote the unscaled fit indices as RMSEA_U, CFI_U, and TLI_U. More details regarding the scaled and unscaled fit indices are described in the next section.

When DWLS is applied to ordered categorical data, many studies have questioned whether the conventional cutoff values for RMSEA, CFI, and TLI suggested by Hu and Bentler (1999) can be applied similarly. Yu (2002) conducted a simulation study in which the sample size, type of model misspecification, and type of variable (i.e., binary, normal, and nonnormal data) were varied, and she concluded that no universal cutoff values seem to work across all conditions for DWLS-scaled model fit indices. Beauducel and Herzberg (2006) also found that the performance of the DWLS-scaled model fit indices is not clear and that different cutoff criteria are needed. Garrido, Abad, and Ponsoda (2016) and Yang and Xia (2015) investigated the utility of RMSEA_S, CFI_S, and TLI_S in determining the number of common factors in exploratory factor analysis, both suggesting that it is difficult to develop a set of cutoff values across all simulation conditions for DWLS. Nye and Drasgow (2011) found that DWLS produced smaller RMSEA_S and larger CFI_S and TLI_S values than did the ML-fit indices using an empirical data set with 9,292 observations. Nye and Drasgow’s simulation study showed similar results, leading them to conclude that the conventional cutoff values do not work when DWLS is applied. DiStefano and Morgan (2014) found that RMSEA_S and CFI_S using DWLS produce problematic results under highly asymmetric categorical distributions, small sample sizes, and dichotomous data. Koziol (2010) found that the differences in RMSEA_S and CFI_S between nested models using DWLS do not have sufficient power to detect noninvariance in the measurement invariance testing context. In a similar context, Sass, Schmitt, and Marsh (2014) suggested that the differences in CFI_S and TLI_S between nested models should be applied with caution, particularly for misspecified models, because these variables’ performance is impacted by both sample size and model complexity.

One alternative to DWLS is the unweighted least squares (ULS) estimator (termed mean- and variance-adjusted unweighted least squares—i.e., ULSMV—in Mplus when robust corrections are implemented; B. O. Muthén et al., 1997). ULS and DWLS with robust corrections were both proposed by B. O. Muthén et al., but the former method has been underutilized, as compared with the latter. We did a search in Google Scholar and located 16 empirical studies before 2016 that applied ULS to Likert-scale data (e.g., Currier & Holland, 2014; De Beer, Pienaar, & Rothmann, 2014; Stander, Mostert, & de Beer, 2014). Simulation studies have found that ULS results in higher nonconvergence rates than does DWLS (Forero, Maydeu-Olivares, & Gallardo-Pujol, 2009), but that it provides slightly more accurate parameter estimates and standard errors than DWLS (Forero et al., 2009; C. H. Li, 2014; Yang-Wallentin, Jöreskog, & Luo, 2010). Savalei and Rhemtulla (2013) further investigated the robust chi-square statistics and concluded that ULS with the mean- and variance-adjusted chi-square statistic outperforms DWLS regarding Type I error rates and power. The performance of RMSEA_S, CFI_S, and TLI_S under ULS has not been extensively evaluated. We found only one such study, performed by Maydeu-Olivares, Fairchild, and Hall (2017), who investigated how the number of categories could impact the ULS-RMSEA_S. They found that ULS-RMSEA_S decreases, and thus results in the loss of power, with more data categories.

On the basis of our literature review, we concluded that the performance of DWLS-RMSEA_S, CFI_S, and TLI_S is elusive, and that no clear guideline exists for goodness-of-fit evaluation for ordered categorical data in SEM. However, researchers in substantive areas are still tempted to apply the conventional cutoff values to DWLS. It is very common to see statements in published articles like “DWLS [or WLSMV] was applied to analyze ordered categorical data. A good model–data fit is indicated by RMSEA < .06, CFI > .95, and TLI > .95 (Hu & Bentler, 1999).” All 16 empirical studies that we found that employed ULS also applied the conventional cutoffs to evaluate the model–data fit. Hu and Bentler and other researchers (e.g., Marsh et al., 2004) have cautioned against the universal use of conventional cutoff criteria, which, unfortunately, has not seemed to stop the widespread use of these cutoffs with other estimation methods such as DWLS and ULS. In this article we take an alternative perspective, to examine the model–data fit evaluation under different estimation methods when ordered categorical data are analyzed. We aimed to show the consequences for model–data fit evaluation that result from applying the conventional cutoffs to DWLS and ULS. Specifically, this article answers the following research question: When a hypothesized model is fitted to a population-level polychoric correlation matrix using ML and results in a specific RMSEA value (e.g., .06), what is the RMSEA value if the same model is fitted to the same matrix using DWLS or ULS? CFI and TLI were investigated in the same manner.

We conducted a simulation study to answer the above research question. Although in SEM applications fit indices are commonly used in sample-level SEM analysis, we decided to conduct the present simulation study at the population level, so that no confounding due to sample fluctuation would be introduced. We made this decision for the following two reasons. First, if the same misspecified model were fit to the same population data but resulted in different fit indices using different estimation methods, then it would be clear that the same value of a fit index tells a different story regarding model–data misfit using different estimation methods. A clear understanding of these fit indices at the population level will be necessary before the sampling properties can be investigated. All the simulation studies we reviewed and cited above were conducted under finite samples; therefore, it is not clear whether the different performance of the fit indices under different estimation methods was due to their population properties, sampling error, or both. Second, although the scaled indices are commonly reported for sample-level analysis in SEM applications, they are calculated without theoretical justification, as has been evidenced by Brosseau-Liard and Savalei (2014) and Brosseau-Liard et al. (2012). As we will show in formulas (see Eqs. 8–13), the unscaled fit indices from ULS and DWLS converge to the theoretical definitions of RMSEA, CFI, and TLI as the sample size increases to infinity, but the scaled fit indices converge to distorted asymptotic values. Therefore, we question the appropriateness of using the scaled fit indices currently implemented in software programs.

We employed Cudeck and Browne’s (1992) simulation technique in order to generate population polychoric correlation matrices with predefined ML-RMSEA values as measures of degrees of model misspecification. The generated matrices were then fitted using DWLS and ULS in order to calculate the corresponding scaled and unscaled DWLS and ULS fit indices. We chose the ML fit indices based on the polychoric correlation matrices as the benchmark for comparison. At the population level, the polychoric correlation matrix is essentially the Pearson correlation matrix for generating continuous data, given that the underlying continuous variables follow a standard multivariate normal distribution. Therefore, the population values of the ML fit indices based on polychoric correlation matrices are the same as those based on the Pearson correlation matrices of continuous data. Because Hu and Bentler’s (1999) cutoff values were developed using the covariance matrices for continuous variables, the population values of ML fit indices using polychoric correlation matrices are consistent with those in Hu and Bentler’s study. It is also important to note that robust corrections are recommended to adjust the chi-square statistic and standard error when ML is employed for polychoric correlation matrices (e.g., Yang-Wallentin et al., 2010).

The next section briefly summaries the fit functions of ML, ULS, and DWLS, as well as the population definitions of RMSEA, CFI, and TLI. Because current software programs (e.g., Mplus and lavaan in R) scale the fit indices such that the indices are functions of the scaled chi-square statistics, we will also compare the scaled fit indices with the unscaled versions. Thereafter, a comparison of RMSEA, CFI, and TLI across the ML, ULS, and DWLS methods is presented using the simulation technique outlined in Cudeck and Browne (1992). Following the simulation study, we take six empirical polychoric correlation matrices reported in published studies, analyze the matrices using ML, ULS, and DWLS, and compare the resulting fit indices across the three estimators. We will show that the conclusions of a model–data fit evaluation can be dramatically different, depending on which estimation method is applied. Finally, suggestions and discussions regarding the application of RMSEA, CFI, and TLI in SEM with ordered categorical data are given.

Fit function, RMSEA, CFI, and TLI

In SEM analysis, it is frequently assumed that a continuous variable underlies an ordered categorical variable (e.g., Olsson, 1979; Pearson, 1904; Tallis, 1962). This underlying continuous variable is categorized into the ordered categorical variable on the basis of a set of threshold values. Under this assumption, the measure of association that is of interest in the modeling is the correlation between the underlying continuous variables, which is termed the polychoric correlation (tetrachoric correlation is a special case in which both ordinal variables have two categories).

To analyze ordered categorical variables in SEM, a three-stage procedure can be applied. The first two steps estimate the thresholds and polychoric correlation matrix, which can be achieved by Olsson’s (1979) two-step ML method, implemented by default in software programs (e.g., Mplus). In the third stage, the estimated threshold values and polychoric correlation matrix are fitted to a hypothesized model using an estimation method (e.g., ML, DWLS, or ULS). The model parameter estimates are then obtained by minimizing a certain fit function, as described below.

The general form of a fit function can be written as

$$ F={\left(\mathbf{s}-\boldsymbol{\upsigma} \left(\boldsymbol{\upomega} \right)\right)}^{\prime }{\mathbf{W}}^{-1}\left(\mathbf{s}-\boldsymbol{\upsigma} \left(\boldsymbol{\upomega} \right)\right). $$

(1)

In Eq. 1, ${\mathbf{s}}^{\prime }=\left({\mathbf{s}}_1^{\prime },{\mathbf{s}}_2^{\prime}\right)$, where s₁ is a column vector containing the thresholds and s₂ contains the nonduplicate unstructured polychoric correlations; ${\boldsymbol{\upsigma}}^{\prime}\left(\boldsymbol{\upomega} \right)=\left({\boldsymbol{\upsigma}}_1^{\prime}\left(\boldsymbol{\upomega} \right),{\boldsymbol{\upsigma}}_2^{\prime}\left(\boldsymbol{\upomega} \right)\right)$, where ω is a vector containing the model parameters and σ₁(ω) and σ₂(ω) are the vectors containing the model-implied thresholds and polychoric correlations, respectively; and W is a weight matrix that is specific to an estimation method. The fit function characterizes the discrepancy between s and σ(ω) . The vector ω is estimated by minimizing F. This study only considered the models with unstructured thresholds such that ${\mathbf{s}}_1^{\prime }-{\boldsymbol{\upsigma}}_1^{\prime}\left(\boldsymbol{\upomega} \right)=\mathbf{0}$.

In Eq. 1, different forms of W lead to different estimators. The weight matrices for ULS and DWLS are

$$ {\mathbf{W}}_{\mathrm{ULS}}=\mathbf{I}, $$

(2)

and

$$ {\mathbf{W}}_{\mathrm{DWLS}}=N\cdot \operatorname{diag}\left(\boldsymbol{\Gamma} \right), $$

(3)

respectively. In Eq. 2, I is an identity matrix. In Eq. 3, N is the sample size, Γ is the asymptotic variance and covariance matrix of thresholds and polychoric correlations, and diag(Γ) is a diagonal matrix with all the diagonal elements the same as the diagonal elements in Γ. The detailed calculation of N ⋅ diag(Γ), which is a function of the thresholds and polychoric correlations, is described in Olsson (1979). Although W_DWLS is expressed as N ⋅ diag(Γ), W_DWLS is not a function of N, because the formula of diag(Γ) has N in the denominator, and thus N in Eq. 3 is canceled out.

It is also possible to fit the polychoric correlation matrix using the ML fit function, but there is no theoretical justification for the resulting robust standard error and chi-square statistic (Yang-Wallentin et al., 2010). The fit function of ML can also be expressed as

$$ {F}_{\mathrm{ML}}=\log \left|\sum \left(\upomega \right)\right|+\mathrm{tr}\left({\mathbf{S}\boldsymbol{\Sigma}}^{-1}\left(\upomega \right)\right)-\log \left|\mathbf{S}\right|-p, $$

(4)

where S is the unstructured polychoric correlation matrix, Σ(ω) is the model-implied polychoric correlation matrix, and p is the number of observed variables.

RMSEA, CFI, and TLI are defined on the basis of the fit function (Bentler, 1990; Bentler & Bonett, 1980; Steiger, 1990; Steiger & Lind, 1980; Tucker & Lewis, 1973). Let H and B denote the hypothesized model and the baseline model (i.e., a model assuming zero correlation between every pair of underlying continuous variables), respectively. $\tilde{F_H}$ and $\tilde{F_{\mathrm{B}}}$ represent the minimized fit functions of H and B at the population level, respectively, and df_H and df_B are the corresponding model degrees of freedom. In the population,

$$ {\mathrm{RMSEA}}_{\mathrm{U}}=\sqrt{\frac{\tilde{F_{\mathrm{H}}}}{df_{\mathrm{H}}},} $$

(5)

$$ {\mathrm{CFI}}_{\mathrm{U}}=1-\frac{\tilde{F_{\mathrm{H}}}}{\tilde{F_{\mathrm{B}}}}, $$

(6)

and

$$ {\mathrm{TLI}}_{\mathrm{U}}=1-\frac{\tilde{F_{\mathrm{H}}}/{df}_{\mathrm{H}}}{\tilde{F_{\mathrm{B}}}/{df}_{\mathrm{B}}}. $$

(7)

The subscript U in Eqs. 5–7 means that the indices are unscaled. Because the mean- and variance-adjusted chi-square is applied in both WLSMV and ULSMV, current software programs (e.g., Mplus and lavaan in R) compute the scaled fit indices as functions of the adjusted chi-square statistic. At the sample level, the scaled indices are calculated as

$$ {\mathrm{RMSEA}}_{\mathrm{S},N}=\sqrt{\frac{{\hat{a}}_{\mathrm{H}}\left(N-1\right)\hat{F_{\mathrm{H}}}+\hat{b_{\mathrm{H}}}}{\left(N-1\right){df}_{\mathrm{H}}}-\frac{1}{N-1}}, $$

(8)

$$ {\mathrm{CFI}}_{\mathrm{S},N}=1-\frac{{\hat{a}}_{\mathrm{H}}\left(N-1\right){\hat{F}}_{\mathrm{H}}+{\hat{b}}_{\mathrm{H}}-{df}_{\mathrm{H}}}{\hat{a_{\mathrm{B}}}\left(N-1\right){\hat{F}}_{\mathrm{B}}+{\hat{b}}_{\mathrm{B}}-{df}_{\mathrm{B}}}, $$

(9)

and

$$ {\mathrm{TLI}}_{\mathrm{S},N}=1-\frac{{\hat{a}}_{\mathrm{H}}\left(N-1\right){\hat{F}}_{\mathrm{H}}+{\hat{b}}_{\mathrm{H}}-{df}_{\mathrm{H}}}{\hat{a_{\mathrm{B}}}\left(N-1\right){\hat{F}}_{\mathrm{B}}+{\hat{b}}_{\mathrm{B}}-{df}_{\mathrm{B}}}\cdot \frac{d{f}_{\mathrm{B}}}{d{f}_{\mathrm{H}}}. $$

(10)

$\hat{a}$ and $\hat{b}$ converge to α and b (i.e., the scaling parameter and shifting parameter, respectively; Asparouhov & Muthén, 2010), and $\hat{F}$ converges to $\tilde{F}$ as N increases to infinity. Therefore, Eqs. 8–10 converge to

$$ {\mathrm{RMSEA}}_{\mathrm{S}}=\sqrt{\frac{a_{\mathrm{H}}\tilde{F_{\mathrm{H}}}}{d{f}_{\mathrm{H}}},} $$

(11)

$$ {\mathrm{CFI}}_{\mathrm{S}}=1-\frac{a_{\mathrm{H}}\tilde{F_{\mathrm{H}}}}{a_{\mathrm{B}}\tilde{F_{\mathrm{B}}}}, $$

(12)

and

$$ {\mathrm{TLI}}_{\mathrm{S}}=1-\frac{a_{\mathrm{H}}\tilde{F_{\mathrm{H}}}}{a_{\mathrm{B}}\tilde{F_{\mathrm{B}}}}\cdot \frac{d{f}_{\mathrm{B}}}{d{f}_{\mathrm{H}}}. $$

(13)

Equations 5 to 7 and 11 to 13 show that both scaled and unscaled RMSEA, CFI, and TLI are functions of the fit function, whose value is dependent on the chosen estimation method. Therefore, given a population polychoric correlation matrix and a hypothesized misspecified model, different estimators can lead to different values of the fit indices. These equations also show that even for the same estimator, the scaled fit indices converge to different population values from unscaled fit indices. In Study 1, we compared each fit index across the three estimators using computer-generated polychoric correlation matrices. In Study 2, we fit six polychoric correlation matrices reported in empirical research using the three estimators. For both studies, we highlighted the potential consequence on the model–data fit evaluation if the conventional cutoffs developed under ML are applied to DWLS and ULS.

Study 1: Comparing fit indices across estimators using population matrices

We employed the simulation technique outlined in Cudeck and Browne (1992) to generate polychoric correlation matrices with target degrees of model misspecification (as measured by RMSEA_U) under ML. We then specified the thresholds for each variable. For each generated matrix and threshold condition, we analyzed the same model using DWLS and ULS to obtain the corresponding model fit indices.

Generation of polychoric correlation matrices

Cudeck and Browne’s (1992) method was applied in order to generate the polychoric correlation matrices with prespecified ML-RMSEA_U values. The resulting matrices had two attributes: When these matrices were analyzed by ML using a prespecified target model, (1) the resulting RMSEA_U value was the same as the prespecified RMSEA_U, and (2) the parameter estimates were the same as those in the prespecified target model. Below we describe the use of this method for generating polychoric correlation matrices in three steps.

The first step was to specify a target model-implied polychoric correlation matrix Σ(ω). Four target CFA models with different numbers of latent factors (one and three) and observed indicators (9 and 18) were used to specify Σ(ω) on the basis of

$$ \boldsymbol{\Sigma} \left(\upomega \right)=\wedge \Phi \wedge {}^{\prime }+\boldsymbol{\Psi}, $$

(14)

where ∧ was the loading matrix, with

$$ {\displaystyle \begin{array}{l}\mathrm{Model}\kern0.28em 1:\wedge {}^{\prime }=\left[.7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em \right]\\ {}\mathrm{Model}\kern0.28em 2:\wedge {}^{\prime }=\left[.7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7.7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em \right]\\ {}\mathrm{Model}\kern0.28em 3:\wedge {}^{\prime }=\left[\begin{array}{c}.7\kern0.28em .7\kern0.28em .7\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em \\ {}0\kern0.28em 0\kern0.28em 0\kern0.28em .\mathrm{7.7.7}\kern0.28em 0\kern0.28em 0\kern0.28em 0\\ {}\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em .7\kern0.28em .7\kern0.28em .7\end{array}\right]\\ {}\mathrm{Model}\kern0.28em 4:\wedge {}^{\prime }=\left[\begin{array}{c}.7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\\ {}0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em \\ {}0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 0\kern0.28em 7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em .7\kern0.28em \end{array}\right]\end{array}} $$

(15)

Φ was the factor covariance matrix, with

$$ {\displaystyle \begin{array}{l}\mathrm{Model}\;1\;\mathrm{and}\kern0.17em \mathrm{Model}\;2:\boldsymbol{\Phi} =\left[1\right]\\ {}\mathrm{Model}\;3\;\mathrm{and}\kern0.17em \mathrm{Model}\;4:\boldsymbol{\Phi} =\left[\begin{array}{ccc}1& .3& .3\\ {}.3& 1& .3\\ {}.3& .3& 1\end{array}\right]\end{array}}, $$

(16)

and Ψ was the residual matrix, with no covariance between any pair of residuals:

$$ {\displaystyle \begin{array}{l}\mathrm{Model}\kern0.28em 1\kern0.28em \mathrm{and}\kern0.34em \mathrm{Model}\kern0.28em 3:\operatorname{diag}\left(\boldsymbol{\Psi} \right)=\left[.51,.51,.51,.51,.51,.51,.51,.51,.51\right]\\ {}\mathrm{Model}\kern0.28em 3\kern0.28em \mathrm{and}\kern0.34em \mathrm{Model}\kern0.28em 4:\operatorname{diag}\left(\boldsymbol{\Psi} \right)=\left[\begin{array}{c}.51,.51,.51,.51,.51,.51,.51,.51,.51,\\ {}.51,.51,.51,.51,.51,.51,.51,.51,.51\end{array}\right]\end{array}}. $$

(17)

The second step was to specify a target ML-RMSEA_U as the measure of the degree of misspecification. We varied the target RMSEA_U from .02 to .12 with an interval of .02, so that the degree of misspecification for the target CFA models ranged from small to large according to the conventional cutoff suggested by Hu and Bentler (1999). We did not include the condition with the target RMSEA_U of 0 because the corresponding analysis model was correctly specified and the fit indices showed perfect fit (i.e., scaled and unscaled RMSEA = 0, CFI = 1, and TLI = 1) at the population level, regardless of the estimator used.

The third step was to construct an error matrix E to obtain the population polychoric correlation matrix S:

$$ \mathbf{S}=\boldsymbol{\Sigma} \left(\boldsymbol{\upomega} \right)+\mathbf{E}. $$

The details of the matrix operations to generate E were described in Cudeck and Browne (1992). Briefly described, E was generated such that two constraints were met: When S was fitted to the target CFA model using ML, the estimated parameters yielded the same values as those in Eqs. 15–17, and the resulting ML-RMSEA_U was equal to the prespecified ML-RMSEA_U value. Because the computation of E involved random-number generation, it was possible to generate many S matrices, each of which resulted in the prespecified ML-RMSEA_U value and parameter estimates when it was fitted to the target CFA model using ML. We generated 200 S matrices for each target ML-RMSEA_U value under each target CFA model.

SAS (SAS Institute, 2015) was used to implement these three steps for generating the polychoric correlation matrices. In sum, 200 (matrices under each condition) × 6 (target ML-RMSEA_U values) × 4 (target CFA models) = 4,800 matrices were generated.

Analyses

Each matrix was fitted to its corresponding target CFA model using ULS and DWLS, with the CALIS procedure in SAS/STAT 14.1 (SAS Institute, 2015). For the ULS scaled indices and DWLS, threshold values need to be specified in order to calculate the weight matrix (W_DWLS), shown in Eq. 3, as well as the a and b parameters in Eqs. 11–13, which were determined using the population thresholds and polychoric correlations (Asparouhov & Muthén, 2010; B. O. Muthén et al., 1997; Olsson, 1979).¹ We varied the number of categories to be either two or four. All ordered categorical variables under each condition had the same set of thresholds. With two categories, the thresholds were either [0] or [1.5] across the variables. With four categories, the thresholds were varied at [– 1, 0, 1] and [0, 1, 2]. The values of [0] and [– 1, 0, 1] resulted in symmetric categorical distributions, whereas [1.5] and [0, 1, 2] resulted in high levels of asymmetry.

The thresholds were not needed to compute the ULS-RMSEA_U, CFI_U, and TLI_U at the population level, for two reasons. First, the threshold structure was saturated—that is, s₁ − σ₁(ω) = 0 in Eq. 1. Second, the weight matrix shown in Eq. 2 is an identity matrix and is not impacted by the threshold values.

The resulting unscaled and scaled variants of RMSEA, CFI, and TLI based on DWLS and ULS were calculated using Eqs. 5–7 and 11–13. The matrices were not analyzed using ML, because Cudeck and Browne’s (1992) method ensured that the ML-RMSEA_U was the same as the prespecified ML-RMSEA_U. In addition, the ML-CFI_U and TLI_U could be calculated using matrix operations. The corresponding ML-CFI_U and TLI_U for each target model are presented in Table 1. Note that, given an ML-RMSEA_U, the resulting ML-CFI_U and TLI_U were expected to differ across different population models (e.g., Lai & Green, 2016).

Table 1 ML-RMSEA_U, -CFI_U, and -TLI_U under each simulation condition

Results

Comparing ML with ULS

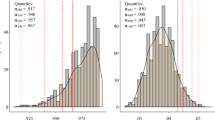
Figure 1 plots the ULS-RMSEA_U for each generated polychoric correlation matrix against the prespecified ML-RMSEA_U. The horizontal and vertical dotted lines represent the conventional cutoff value of RMSEA (i.e., .06). For all the matrices, the ULS-RMSEA_U was lower than the ML-RMSEA_U, suggesting that the models had a greater tendency to be considered acceptable using ULS. Figure 2 compares ULS-RMSEA_S with ML-RMSEA_U. The left panel presents the results when each variable had the threshold of [0], and the right panel has the threshold equal to [1.5]. Similar to ULS-RMSEA_U, ULS-RMSEA_S was consistently smaller than ML-RMSEA_U. With more extreme thresholds, ULS-RMSEA_S became even lower, and thus suggesting a better fit.

Fig. 1

Comparison between ML-RMSEA_U and ULS-RMSEA_U. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using ULS, if RMSEA < .06 is used as the criterion of acceptable fit.

Fig. 2

Comparison between ML-RMSEA_U and ULS-RMSEA_S when the data are binary. The left panel has threshold = [0], and the right panel has threshold = [1.5]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using ULS, if RMSEA < .06 is used as the criterion of acceptable fit.

Using RMSEA < .06 as the cutoff, many matrices (those marked as crosses in Figs. 1 and 2) resulted in poor fit when analyzed by ML but acceptable fit according to either ULS-RMSEA_U or ULS-RMSEA_S. For example, when the ML-RMSEA_U was .10, all the matrices in the one-factor models and in the three-factor models with 18 items showed ULS-RMSEA_U and RMSEA_S < .06. In addition, for a given ML-RMSEA_U, the one-factor models tended to result in a lower ULS-RMSEA_U and -RMSEA_S than did the three-factor models. This pattern suggests that ULS-RMSEA_U appeared to be less likely to detect model–data misfit in more parsimonious models than in more complex models if the same cutoff was applied.

Figures 3 and 4 plot the ULS-CFI_U and -CFI_S, respectively, against the ML-CFI_U. Both the ULS-CFI_U and -CFI_S were higher than the ML-CFI_U. The majority of the ULS-CFI_U and -CFI_S values were above .95 (except for several analyses with three factors and nine items), whereas the corresponding ML-CFI_U values fell below .95. For example, under the three-factor model with 18 items, when ML-CFI_U was approximately .77, the corresponding ULS-CFI_U and -CFI_S values were generally above .95. This pattern suggests that ULS-CFI_U and -CFI_S were much less sensitive to model misspecification than was ML-CFI if the same cutoff was applied. The results for TLI had very similar patterns, and thus are not reported.

Fig. 3

Comparison between ML-CFI_U and ULS-CFI_U. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using ULS, if CFI > .95 is used as the criterion of acceptable fit.

Fig. 4

Comparison between ML-CFI_U and ULS-CFI_S when the data are binary. The left panel has threshold = [0], and the right panel has threshold = [1.5]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using ULS, if CFI > .95 is used as the criterion of acceptable fit.

Comparing ML with DWLS

Figures 5 and 6 show the values of DWLS-RMSEA_U and -RMSEA_S, respectively, for data with two categories. The patterns of DWLS-RMSEA_U and -RMSEA_S were similar to those from ULS, in that all the values were lower than those for ML-RMSEA_U. DWLS-RMSEA_U and -RMSEA_S were also less likely to discover model–data misfit with 18 than with nine items and with the one-factor than with the three-factor models. DWLS-RMSEA_U and -RMSEA_S were both dependent upon the categorical distribution, because its values decreased (all below .03) as the categorical distribution became asymmetric. Appendix 1 shows DWLS-RMSEA_U and -RMSEA_S, respectively, for data with four categories. Similarly, the resulting values were smaller than those for ML-RMSEA_U, especially when the target models had 18 items and the categorical distribution was asymmetric. The impact of the number of latent factors on the DWLS indices was less clear. DWLS-RMSEA_U was lower in the one-factor than in the three-factor models, except for the analyses with 18 items and ML-RMSEA_U = .12.

Fig. 5

Comparison between ML-RMSEA_U and DWLS-RMSEA_U when the data are binary. The left panel has threshold = [0], and the right panel has threshold = [1.5]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if RMSEA < .06 is used as the criterion of acceptable fit.

Fig. 6

Comparison between ML-RMSEA_U and DWLS-RMSEA_S when the data are binary. The left panel has threshold = [0], and the right panel has threshold = [1.5]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if RMSEA < .06 is used as the criterion of acceptable fit.

Figures 7 and 8 present the DWLS-CFI_U and -CFI_S, respectively, when the data had two categories. ML-CFI_U ranged from .77 to .99, but DWLS-CFI_U and -CFI_S were mostly greater than .95. DWLS-CFI_U and -CFI_S appeared to be relatively stable across conditions with different thresholds and numbers of categories. Again, if CFI > .95 was adopted as the indication of an acceptable model, the model was more likely to be judged a good model when DWLS rather than ML was used, especially for the target models with one factor or with nine items. The results for TLI were extremely similar to those for CFI, and thus are not reported.

Fig. 7

Comparison between ML-CFI_U and DWLS-CFI_U when the data are binary. The left panel has threshold = [0], and the right panel has threshold = [1.5]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if CFI > .95 is used as the criterion of acceptable fit.

Fig. 8

Comparison between ML-CFI_U and DWLS-CFI_S when the data are binary. The left panel has threshold = [0], and the right panel has threshold = [1.5]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if CFI > .95 is used as the criterion of acceptable fit.

Implications of Study 1

On the basis of the conditions we manipulated in Study 1, ULS- and DWLS-RMSEA_U and -RMSEA_S were smaller than those from ML-RMSEA_U, and ULS- and DWLS-CFI_U values were larger than those from ML-CFI_U. Therefore, both scaled and unscaled RMSEA, CFI, and TLI from ULS and DWLS are more likely than ML to indicate better model–data fit when the same misspecified model is analyzed. If we continue applying Hu and Bentler’s (1999) cutoffs developed under ML to ULS and DWLS in SEM analyses with ordered categorical variables, in the long run we would expect that more models that should have been considered poor fit would accumulate in the published literature and be considered acceptable fit. In addition, both unscaled and scaled ULS- and DWLS-CFI and -TLI were mostly clustered at large values (i.e., > .95), making them less useful in differentiating “unacceptable” from “acceptable” models. Because we investigated population-level fit indices, the conclusions above apply to data with large-enough sample sizes.

Study 2: Comparing fit indices across estimators using empirical polychoric correlation matrices

In Study 1 we employed polychoric correlation matrices using simulated matrices. To further demonstrate the consequences of applying the conventional cutoffs to analyses with ULS and DWLS, in Study 2 we applied six empirical polychoric correlation matrices (labeled as M1–M6) that have been reported in published research articles (Fernandez & Moldogaziev, 2013; Iglesias, Burnand, & Peytremann-Bridevaux, 2014; MacInnis, Lanting, Rupert, & Koehle, 2013; Martínez-Rodríguez et al., 2016; Nguyen et al., 2016; Pettersen, Nunes, & Cortoni, 2016) in the behavioral sciences (e.g., sexual behavior, employee performance, and aggression). These articles were located by a nonexhaustive search using Google Scholar from 2013 to 2016 and the search term “polychoric correlation matrix.” All six of the articles reported polychoric correlation matrices and applied SEM with ordered categorical variables. We treated these matrices as the population matrices and fitted them to the models that were considered to be acceptable in their corresponding articles, using ML, ULS, and DWLS. The six polychoric correlation matrices are available in Appendix 2. Our goal was to replicate the conclusion from Study 1 using real polychoric correlation matrices reported in empirical research. That is, we aimed to show that both unscaled and scaled ULS- and DWLS-RMSEA, -CFI, and -TLI tend to indicate a better model–data fit than does ML when analyzing ordered categorical variables.

Table 2 summarizes the target models that were used to analyze M1–M6, which include five CFA models and one full structural model, with different numbers of factors (one to four) and different test lengths (5–12 items). For the ML and ULS unscaled indices, the threshold values were not needed to calculate the fit indices at the population level. However, for the ULS scaled indices and for DWLS the threshold values were required, and we manipulated them in the same way as in Study 1.² The resulting RMSEA, CFI, and TLI values are presented in Table 2. The results were consistent with those from Study 1, in that the DWLS- and ULS-RMSEA_U and -RMSEA_S values were smaller than those from ML-RMSEA_U, and the DWLS- and ULS-CFI_U and -CFI_S values were larger than those from ML-CFI_U. The patterns for TLI were similar to those for CFI. For example, for M1, the ML-RMSEA_U, -CFI_U, and -TLI_U values were .245, .919, and .879, all suggesting severe misfit. However, ULS and DWLS both produced indices that suggested much better fit, especially for CFI and TLI (> .998, reaching the ceiling and suggesting an excellent fit), regardless of whether or not they were scaled.

Table 2 Model fit indices calculated using the six polychoric correlation matrices in Study 2

We also selected M1, M2, and M4 to investigate whether the conclusions above could be observed in the sample-level data. The sample size was fixed at 500, which is considered a moderate sample size in behavioral research. The results and more details of the simulation are presented in Appendix 3, consistently showing that ULS and DWLS resulted in overoptimistic unscaled and scaled fit indices as compared with ML.

Discussion

Given the lack of investigation of the ULS and DWLS fit indices, in this article we compared them with their ML counterparts at the population level. Study 1 used Cudeck and Browne’s (1992) simulation technique and showed that both the unscaled and scaled RMSEA values from ULS and DWLS were smaller than the ML-RMSEA_U values. CFI and TLI, in contrast, from ULS and DWLS had values larger than those from ML. In Study 2 we employed six polychoric correlation matrices reported in published research and found consistent results. In summary, the ULS- and DWLS-RMSEA, -CFI, and -TLI values, scaled or not, are more likely to indicate a better model–data fit than are the ML fit indices when the same misspecified model is analyzed and when the same sets of conventional cutoff values are adopted. Therefore, applying the conventional cutoffs to ULS and DWLS can lead in the long run to the accumulation of models with severe misfit that are nonetheless considered acceptable, even in substantive research with sufficient sample sizes.

Because in this study we have primarily compared the asymptotic values of the fit indices across estimation methods, the conclusions above only apply to studies with sufficient sample sizes. For example, with a sample size of 500, ULS and DWLS yield overoptimistic fit indices, as is shown in Appendix 3. The results for the asymptotic values of the DWLS fit indices are consistent with those based on finite samples in Nye and Drasgow (2011). Nye and Drasgow first employed a dataset consisting of 9,292 examinees and showed that DWLS produced smaller RMSEA_S and larger CFI_S and TLI_S values than did ML on the basis of polychoric correlation matrices, especially when the data were dichotomized. Nye and Drasgow further implemented a simulation study to examine what cutoff values would be appropriate for DWLS fit indices under finite samples (i.e., 400, 800, and 1,600) with dichotomous data, and found that DWLS-CFI_S and TLI_S were mostly .99 for both moderately and severely misspecified models. However, we did not explore the results with smaller sample sizes. Savalei and Rhemtulla (2013) recommended that samples of at least 150 observations are needed for either binary or three-category data. With a smaller sample in conjunction with asymmetric categorical distributions, the expected values of fit indices across random samples might be very different from the population values of the indices.

Strong arguments against the application of RMSEA, CFI, and TLI and their conventional cutoff values have been raised in the SEM literature (e.g., Barrett, 2007; Marsh et al., 2004; McIntosh, 2007). However, before better alternatives are proposed and accepted by SEM practitioners, the application of these fit indices will continue in most SEM studies. We do not aim to directly address the question of what new cutoff values should be employed, partly because empirical Type I error rates and power have not been investigated for finite samples. However, this article delivers two messages that are related to the use of cutoff values in SEM with ordered categorical variables. First, for both ULS scaled indices and DWLS, no universal cutoff values are appropriate; the values of the indices are contingent upon the number of categories and the threshold values. The cutoff values thus also need to be specific to the thresholds, which is impractical. Second, both scaled and unscaled ULS- and DWLS-CFI and -TLI are very insensitive to model misspecification, because they mostly cluster above .95 under our manipulated conditions. In addition, in Study 2, even when the ML indices suggested severe misfit, both the unscaled and scaled ULS- and DWLS-CFI and -TLI values were still above .989.

The general consensus is that a larger RMSEA and smaller CFI and TLI values indicate worse fit, which prompts researchers to modify their models and search for a better explanation of the relationship among variables. However, the current practice has evolved into a stage at which the fit indices serve as the criteria (and the sole criteria, in many situations) for determining whether to accept or reject a hypothesized model. As long as the values of the fit indices reach a “publishable level” (e.g., RMSEA < .06), model respecification may be terminated. Given that the DWLS and ULS fit indices tend to show a better model–data fit evaluation than do ML fit indices when the same misspecified model is analyzed, we argue that surpassing a set of cutoff values should not serve as the only justification for the acceptance of a model. It would be more appropriate to consider RMSEA, CFI, and TLI as diagnostic tools for model improvement. A statement such as “because the RMSEA, CFI, and TLI values suggest good fit, this model was chosen as the final model” is not sufficient. Achieving a set of desired values of RMSEA, CFI, and TLI (e.g., according to the conventional cutoffs) is only one marker showing that the model improvement may be successful. Thereafter, one still needs to explain whether other options exist to improve the model, why the options are or are not adopted, and, as was suggested by Barrett (2007), what are the substantive scientific consequences of considering this model to be the final one.

When implementing Study 2, we initially attempted to replicate the results on the basis of the six articles we found. However, we could not achieve this purpose, because neither the threshold values nor the weight matrix used to compute the fit function was reported. We have also found that many studies have fit their models to polychoric correlation matrices but reported Pearson correlation matrices instead by treating the ordered categorical variables as continuous. Misunderstanding exists regarding the application of polychoric correlation. To improve the transparency and reproducibility of published results, we recommend that researchers report the polychoric correlation matrices associated with the threshold values (or the proportions of observed responses in each category).

When a mean- and variance-adjusted chi-square statistic is employed in WLSMV and ULSMV, software programs by default compute scaled fit indices that do not converge to the definitions of RMSEA, CFI, and TLI. Brosseau-Liard, Savalei, and Li (2012) first raised this concern using continuous data analyzed by ML with Satorra and Bentler’s (1994) robust correction. Brosseau-Liard and Savalei (2014), Brosseau-Liard et al. (2012), and Xia, Yung, and Zhang (2016) showed that the scaled RMSEA, CFI, and TLI values under continuous data implemented in SEM software programs (e.g., EQS, Mplus, and the CALIS procedure in SAS/STAT 14.1; Bentler, 2008; L. K. Muthén & Muthén, 2015; SAS Institute, 2015) converge to values that are different from the population definitions of RMSEA, CFI, and TLI. Because a similar logic lies behind the robust corrections to ULS and DWLS (e.g., Savalei, 2014) when analyzing ordered categorical variables, the scaled fit indices also converge to population values that deviate from their definitions, as we have demonstrated in Eqs. 8–13. Our study evidences that both the unscaled and scaled fit indices for ULS and DWLS can be problematic, in that they all appear to be insensitive to model misspecification if Hu and Bentler’s cutoff values are applied. Future studies will need to seek alternative methods (e.g., Yuan & Marshall, 2004; Zhang, 2008) for goodness-of-fit evaluation with ordered categorical data.

Appendices

Appendix 1: Additional results for Study 1

The results for the fit indices for conditions with four categories were reported in Figs. 9, 10, 11, 12, 13 and 14. The patterns were similar to the conditions with two categories. That is, ULS and DWLS produced smaller unscaled and scaled RMSEA values and larger unscaled and scaled CFI and TLI values than did ML-RMSEA_U.

Fig. 9

Comparison between ML-RMSEA_U and ULS-RMSEA_S when data are four-category. The left panel has threshold = [– 1, 0, 1], and the right panel has threshold = [0, 1, 2]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using ULS, if RMSEA < .06 is used as the criterion of acceptable fit.

Fig. 10

Comparison between ML-CFI_U and ULS-CFI_S when data are four-category. The left panel has threshold = [– 1, 0, 1], and the right panel has threshold = [0, 1, 2]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using ULS, if CFI > .95 is used as the criterion of acceptable fit.

Fig. 11

Comparison between ML-RMSEA_U and DWLS-RMSEA_U when data are four-category. The left panel has threshold = [– 1, 0, 1], and the right panel has threshold = [0, 1, 2]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if RMSEA < .06 is used as the criterion of acceptable fit.

Fig. 12

Comparison between ML-RMSEA_U and DWLS-RMSEA_S when data are four-category. The left panel has threshold = [– 1, 0, 1], and the right panel has threshold = [0, 1, 2]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if RMSEA < .06 is used as the criterion of acceptable fit.

Fig. 13

Comparison between ML-CFI_U and DWLS-CFI_U when data are four-category. The left panel has threshold = [– 1, 0, 1], and the right panel has threshold = [0, 1, 2]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if CFI > .95 is used as the criterion of acceptable fit.

Fig. 14

Comparison between ML-CFI_U and DWLS-CFI_S when data are four-category. The left panel has threshold = [– 1, 0, 1], and the right panel has threshold = [0, 1, 2]. The crosses represent the matrices on the basis of which the hypothesized models are considered unacceptable using ML but acceptable using DWLS, if CFI > .95 is used as the criterion of acceptable fit.

Appendix 2: The six polychoric correlation matrices in Study 2

The six polychoric correlation matrices in Study 2 are presented in Tables 3, 4, 5, 6, 7 and 8. The analysis model for each matrix is described below. We use “F” to indicate latent factors, “V” to indicate items. “by” means “measured by” and “on” means “regressed on.”

CFA model for M1:

• F by V1–V7.

CFA model for M2:

• F1 by V1–V5; F2 by V6–V9; F3 by V10–V12.

CFA model for M3:

• F1 by V1–V3; F2 by V4–V6; F3 by V7–V9; F4 by V10–V12.

CFA model for M4:

• F by V1–V11;

Nonrecursive structural model for M5:

• F1 by V1–V4; F2 by V5–V6; F3 by V7–V8; F4 by V9–V10.

• F2 on F1; F3 on F1; F4 on F1; F3 on F2; F2 on F3; F3 on F4.

CFA model for M6:

• F by V1–V5.

Table 3 Polychoric Correlation Matrix 1 (Martínez-Rodríguez et al., 2016)

Table 4 Polychoric Correlation Matrix 2 (Nguyen et al., 2016)

Table 5 Polychoric Correlation Matrix 3 (Pettersen et al., 2016)

Table 6 Polychoric Correlation Matrix 4 (Iglesias et al., 2014)

Table 7 Polychoric Correlation Matrix 5 (Fernandez & Moldogaziev, 2013)

Table 8 Polychoric Correlation Matrix 6 (MacInnis et al., 2013)

Appendix 3: Results for the sample-level simulation

Sample-level simulation was conducted in order to further explicate the differences between ML, ULS, and DWLS fit indices. We selected three of the matrices (i.e., Matrices 1, 2, and 4) in Study 2 to generate sample data, because they yielded ML-RMSEA_U > .10, ML-CFI_U < .95, and ML-TLI_U < .95. The procedure of this simulation is described below:

• We first generated continuous data following a standard multivariate normal distribution. The continuous data were analyzed by the normal-theory ML estimator. Hu and Bentler’s (1999) cutoff values based on continuous data were for an ML analysis. Therefore, we used the resulting fit indices as the benchmarks for comparison.

• We categorized the continuous data using threshold values. For two-category data, we employed [0] or [1] as the threshold value for every item. For four-category data, the thresholds were either [– 1, 0, 1] or [0, 1, 2]. The threshold manipulation was consistent with that at the population level in Study 2.

• The ordered categorical data were analyzed using the lavaan package in R, using ULSMV and WLSMV. The unscaled and scaled indices were recorded, and their means are reported in Table 9.

The number of replication was 1,000, and sample size was fixed at 500.

The results for the sample-level simulation were consistent with those of Study 2. That is, ULS and DWLS produced overoptimistic unscaled and scaled fit indices as compared with ML, especially for CFI and TLI.

Table 9 Means of model fit indices when sample size is 500