Some task demands induce collapsing bounds: Evidence from a behavioral analysis

Abstract

Traditional models of choice-response time assume that sensory evidence accumulates for choice alternatives until a threshold amount of evidence has been obtained. Although some researchers have characterized the threshold as varying randomly from trial to trial, these investigations have all assumed that the threshold remains fixed across time within a trial. Despite decades of successful applications of these models to a variety of experimental manipulations, the time-invariance assumption has recently been called into question, and a time-variant alternative implementing collapsing decision thresholds has been proposed instead. Here, we investigated the fidelity of the collapsing threshold assumption by assessing relative model fit to data from a highly constrained experimental design that coupled a within-subject mixture of two classic response time paradigms—interrogation and free response—within a random dot motion (RDM) task. Overall, we identified strong evidence in favor of collapsing decision thresholds, suggesting that subjects may adopt a dynamic decision policy due to task characteristics, specifically to account for the mixture of response time paradigms and motion strengths across trials in the mixed response signal task. We conclude that time-variant mechanisms may serve as a viable explanation for the strategy used by human subjects in our task.

Introduction

Many aspects of everyday decisions require that we not only integrate information but also weigh the information appropriately with respect to time. For example, when a soccer player notices a window of opportunity, she might be diligent in aiming for the illustrious top-left corner, but she also must take into account that among the league’s elite defenders, she will have only seconds before her window closes. While it would be ideal to have the most accurate shot possible, the shot itself presents a possibility of a goal, whereas a block by the defender suffers an unfortunate fate. Hence, the accuracy of the shot must be traded for the amount of available time as the defender approaches.

While it is undoubtedly clear that time matters when making decisions, it is often not taken seriously when studying simple decisions such as those commonly used in perceptual decision-making tasks. Most theoretical accounts simply assume that information is integrated in a time-invariant manner, and the decision depends on a fixed policy that is established prior to encountering the alternatives. Recently, these theoretical accounts have been scrutinized because they fail to capture important trends in behavioral data under some specific tasks (e.g., Cisek, Puskas, & El-Murr, 2009; Malhotra, Leslie, Ludwig, & Bogacz, 2017; Purecell et al., 2010; Purcell, Schall, Logan, & Palmeri, 2012; Shadlen & Kiani, 2013; Thura, Beauregard-Racine, Fradet, & Cisek, 2012), and there is a growing body of literature identifying neural computations that are clearly related to time, but not information (e.g., van Vugt, Simen, Nystrom, Holmes, & Cohen, 2012; Wyart, De Gardelle, Scholl, & Summerfield, 2012). Although quite mixed, most of the evidence for time-varying decision policies is garnered when using sophisticated stimuli whose properties have a temporal component, where the average rate of evidence accumulation is controlled directly by the stimulus. As a result, proponents of time-invariant decision policies have not considered these effects to be problematic for extant theoretical accounts.

The central thesis of this article is that in addition to stimuli, task demands could also induce a time-varying decision policy. Here, we examine the impact of task characteristics on the decision policy in a conventional, two-alternative, forced choice task. We use standard stimuli that are dynamic, but stationary, meaning that while the particular presentation changes continuously through time, the changes happen at a fixed rate, and so they are time-invariant. As for the elicitation procedure, we use a simple interrogation (also known as the signal-to-respond) paradigm, where the amount of integration time is treated as an independent variable. The novel aspect of our task is the ability for subjects to “opt out” of the trial by responding prior to the go cue. The opt-out strategy has been used to collect unique information in other domains, such as when obtaining measures of confidence (Kiani & Shadlen, 2009). After investigating a number of decision model variants, we ultimately conclude that models with time-variant decision policies provided the best account of our data.

The outline of this article is as follows. First, we discuss the evidence both for and against time-invariant decision-making, where we place special emphasis on the types of stimuli used and the task demands. Second, we discuss the basic details of our task, and we explain why the task demands used here might induce a time-variant policy. Third, we present the mathematical details of the models used to explain the data from our task and specifically how time-variance is imposed. In this section, we also show how time-invariant and time-variant models make different hypothetical predictions for data from our task, emphasizing the critical opt-out contin- gency. Fourth, we present the methods of our task and model fitting procedure. Fifth, we discuss a number of results, from the raw empirical data to the model-fitting results. Finally, we close with a brief discussion of how our task relates to the debate about time-invariance in decision-making.

The interaction between time and evidence

Currently, the most successful attempts to explain and understand perceptual decision-making behavior in a 2AFC framework involve sequential sampling theory (Stone, 1960; Laming, 1968; Ratcliff, 1978; Ratcliff & Rouder, 1998). In their most basic form, models that embody sequential sampling theory assume that decisions are made by sequentially accumulating sensory evidence from a start- ing point toward a decision threshold. However, as we will discuss below, the implementation of the decision threshold within the model is contingent on the elicitation procedure.

The general class of sequential sampling models have enjoyed widespread success as they have continued to successfully account for a variety of empirical benchmarks observed in decision-making tasks. One of the most success- ful instantiations of sequential sampling theory is the diffusion decision model (DDM; Ratcliff, 1978), which assumes that decisions are based on the continuous accumulation of noisy sensory evidence across time, gradually evolving from an initial starting point toward one of two boundaries, each representing a particular choice alternative. Since its inception, the DDM has successfully explained data from a variety of topics including aging (Ratcliff, Thapar, & McKoon, 2003, 2007), memory (Ratcliff, 1978, 1981; Ratcliff & Rouder, 1998; Ratcliff & McKoon, 2008), and visual processing (Ratcliff & Rouder, 2000; Smith, Ratcliff, & Wolfgang, 2004).

However, despite the model’s ability to account for behavioral data, recent literature has noted that it suffers from a lack of neural plausibility in that it does not provide an explicit explanation for how its mechanisms are imple- mented in the brain. Ditterich (2006a) describes this problem in terms of a “black box” view of cognitive research, such that there is a clear separation between models of behavior and the actual neural mechanisms that produce said behavior. While choice accuracy and response times can be modeled with the hypothesized parameters of the DDM, the black box view asserts that one’s knowledge remains incomplete if the model fits cannot be substantiated by the true neural correlates (but see Turner, Van Maanen, & Forstmann, 2015, for such an analysis). In other words, if we are to assume that it is the ground truth of the decision-making process, there needs to be a more convincing link between the parameters governing the behavioral response and the observed neural activity (Ditterich, 2006a, b; Schall, 2004; Turner, Forstmann, Love, Palmeri, & Van Maanen, 2017).¹

Urgency

Unsatisfied by the lack of a mechanistically plausible account of trial-to-trial variability in the decision process, Ditterich (2006a) proposed a time-variant model that assumed a gain function on accuracy as time increases within a trial, represented as a logistic curve. In this regime, accumulating evidence has an initially higher gain to avoid fast errors, but as time increases, the gain asymptotes such that accumulating more evidence does not necessarily produce increases in accuracy.

To this end, Ditterich (2006a) fit a variant of the DDM that assumed (1) no between-trial variability in starting point, (2) between-trial variability in the drift rate, and (3) an accumulation process with an urgency signal to both behavioral and neural data from a random dot motion task (Roitman and Shadlen, 2002). Ditterich (2006a) found that only the time-variant model could account for both the correct and error response time distributions and accurately predict neural firing rates.

Following Ditterich (2006a), human EEG studies have identified temporal components of the decision process independent of the strength of evidence using spectral analyses (van Vugt et al., 2012; Wyart et al., 2012), and new models using time-dependent gating mechanisms have provided better accounts of certain behavioral and neurophysiological data than time-invariant models in both traditional and novel experimental tasks (Cisek et al., 2009; Purcell et al., 2010, 2012; Thura et al., 2012).

Collapsing bounds

Recently, a similar mechanism for time variance has been proposed, where the bounds of the DDM collapse (i.e., move toward the starting point) with increases in time (Bowman, Kording, & Gottfried, 2015; Shadlen & Kiani, 2013. These models are mathematically similar to the urgency models above and provide similarly effective accounts of behavioral data. The effective difference is that for more difficult decisions, responses are faster when the bounds collapse than when they do not. This small change produces response time distributions that are less skewed (Hawkins, Forstmann, Wagenmakers, Ratcliff, & Brown, 2015). Much like the success of the urgency gating model, models with collapsing decision boundaries have proven more effective in fitting specific neurophysiological and behavioral data than time-invariant competitors (e.g., Bowman et al., 2015; Cisek et al., 2009; Ditterich, 2006a; Gluth, Rieskamp, & Buchel, 2012).

The plausibility of the collapsing boundary assumption initially garnered support by measuring choice confidence through post-decision wagering tasks (Hampton, 2001; Kiani & Shadlen, 2009; Shields, Smith, & Washburn, 1997), where the collapsing bounds assumption served as a better account of data in tasks where the reliability of the stimuli was unknown (i.e., varied across trials). van Maanen, Fontanesi, Hawkins, and Forstmann (2016) provided both behavioral and neural evidence supporting the idea of collapsing decision thresholds and urgency using an expanded judgment task, where they manipulated the rate of evidence accumulation in order to “expand” the average decision time. Using this strategy, van Maanen et al., (2016) found that as the average rate of accumulation decreased and the average decision time increased, participants were more willing to form a response on less overall stimulus information according to an ideal observer model. The pattern of evidence needed to form a response conditional on the time of the response formed an approximately linear function, suggesting time-variance similar to the other models discussed in this section (e.g., Bowman et al., 2015; Cisek et al., 2009; Drugowitsch, Moreno-Bote, Churchland, Shadlen, & Pouget, 2012).

Push back

Although the evidence is building for the presence of time-variant decision policies, there is also evidence continuing to support time invariance. In the most extensive comparison of time-variant and time-invariant models to date, Hawkins et al., (2015) fit variants of a diffusion model with fixed boundaries, variants of a diffusion model with collapsing boundaries, and a variant of the urgency gating model to a variety of human and primate data sets to determine which of the three models best characterized the decision-making process of each subject across all the tasks. The results across species were mixed, with data from the human subjects being best accounted for by the time-invariant models and data from the non-human primates being best accounted for by the time-variant models.

In a similar type of analytic strategy, Voskuilen, Ratcliff, and Smith (2016) investigated time-variant and time-invariant models by fitting these models to several sets of data from numerosity judgment and random dot motion tasks. Similar to Hawkins et al., (2015) and Voskuilen et al., (2016) argued that the properties of the stimuli themselves in tasks like the expanded judgment tasks (e.g., Cisek et al., 2009; van Maanen et al., 2016) were a likely contributor to the evidence supporting time-variant models. After fitting a class of models to data with a model comparison technique argued to be more sensitive to the functional form of each model (i.e., the parametric bootstrap cross-fitting method; Wagenmakers, Ratcliff, Gomez, and Iverson, 2004), the authors found that the time-invariant model provided a better fit to the majority of data. Their analyses support the notion that speeded judgments are better captured by time-invariant decision policies, whereas expanded judgments are better captured by time-variant decision policies.

Inducing collapsing bounds via task demands

While most of the evidence supporting collapsing boundaries has been garnered in experiments that use time-variant stimuli, our hypothesis was that some task demands may also induce a collapsing bound decision policy. Referring back to the example from the introduction, while in most cases we may prefer to maximize accuracy (e.g., our probability of scoring a goal), under conditions where time will expire (e.g., an approaching defender), it is better to make a choice on the basis of only partial information (e.g., knowing where the goal is, but not the location of the goalie). A long history of decision-making research agrees that humans are able to trade accuracy for speed in remarkably flexible ways (Bogacz, Wagenmakers, Forstmann, & Nieuwenhuis, 2010; Forstmann et al., 2008; Garrett, 1922; Pleskac & Busemeyer, 2010; Ratcliff & Rouder, Wickelgren, 1998; 1977) and weigh information differently depending on the time at which it was acquired (Tsetsos et al., 2011). Given these findings, we hypothesized that manipulating the amount of time a subject could integrate stimulus information could make the subject more sensitive to the temporal aspects of integration, thereby inducing a time cost for further integration. In other words, by creating an environment where the amount of integration time was uncertain, we could induce a collapsing boundary.

For our task, we used an interrogation paradigm, otherwise known as a signal-to-respond paradigm. The interrogation paradigm has been used as an elicitation procedure in a variety of tasks (e.g., Corbett & Wickelgren, 1978; Dosher, 1976, 1979, 1981, 1982, 1984; Gao, Tortell, & McClelland 2011; Kounios, Osman, & Meyer 1987; McElree & Dosher, 1993; Meyer, Irwin, Osman, & Kounios, 1988; Ratcliff, 2006; Reed, 1973, 1976; Schouten & Bekker, 1967; Turner, Gao, Koenig, Palfy, & McClelland, 2017; Usher & McClelland, 2001; Wickelgren, 1977; Wickelgren & Corbett, 1977) and has a few desirable properties. Perhaps the most important feature of the interrogation paradigm is that it allows researchers to track response accuracy as a function of integration time, giving insight into the points in time at which accuracy grows away from chance, asymptotes, and interpolates between these two extremes.

Usher and McClelland (2001) used the interrogation paradigm as a way of discriminating between two models of perceptual integration by assuming that within this paradigm, decision boundaries were not used when making the choice. Instead, Usher and McClelland (2001) assumed that observers continued to integrate information until a go cue was presented. Ratcliff (2006) argued that the interrogation paradigm itself did not necessarily preclude the presence of a decision boundary. He argued that the data obtained for a given go cue lag contained some decisions based on integrated information up to the go cue, but also contained some decisions that were essentially made prior to the go cue (i.e., a threshold amount of evidence had already been acquired). The probability of an observer making a decision prior to the go cue could be calculated from the DDM with decision boundaries in tact (also see Ratcliff, 1988). When modeling the choice probabilities as a mixture of two different response contingencies, Ratcliff found that the two models used in Usher and McClelland (2001) could not be distinguished reliably.

While the modeling work of Ratcliff (2006) shows that decision boundaries are still a concern within the interrogation paradigm, there are two points that can be experimentally improved upon for our purposes. First, Ratcliff (2006) collected data from subjects in either the free response or interrogation paradigm, and these two task demands served as separate conditions within the experiment. Second, the elicitation procedure within the classic interrogation paradigm (e.g., Ratcliff, 2006) confounds our ability to separate decision processes that terminate prior to the go cue and those that terminate after the go cue. While the model Ratcliff used (and one of the variants we will use below) can clearly make separate predictions about the probability of these two events, because the data do not inform us about the relative probabilities of these two events, the model is only weakly constrained.

To rectify the issues described above, we extended the basic interrogation paradigm by including the possibility of “opting out” within each trial. The motivation for this feature comes from the additional constraint it can provide in estimating decision states, such as in Kiani and Shadlen (2009) to reveal choice confidence. For a given trial, we will present each stimulus for some pre-determined amount of time (i.e., an independent variable). At the end of this time, we will remove the stimulus, which serves as the cue to respond. However, if subjects are sure of their response before the stimulus disappears, they can provide a response at a time of their choosing, as they might in a free response paradigm. Because our task also involves a mixture of stimulus coherencies, we should expect these coherencies to modulate the probabilities of responding prior to and after the go cue, revealing better insights to the decision dynamics. By including the opt-out procedure, we obtain data on both decisions that were terminated prior to the go cue and those that were terminated after the go cue, thereby eliminating the confound of the standard interrogation paradigm described above.

Modeling the mixed response signal paradigm

In this section, we describe the boundary details of the diffusion decision model. Although Ratcliff (2006) and Usher and McClelland (2001) have compared models such as the DDM and Leaky Competing Accumulator (LCA) model, we only examine the DDM here as the purpose of our article is to investigate whether fixed or collapsing boundaries provide the best account of our data, not different model architectures. As many readers are already familiar with the specific details of the DDM, we will turn our focus to how the decision thresholds in each form of the DDM under investigation in this article are instantiated. Interested readers should look to the Supplementary Materials for details regarding the evolution of evidence within the DDM.

Fixed boundaries

The fixed boundary model is the most common instantiation of the DDM (Ratcliff, 1978, 1981; Ratcliff & McKoon, 2008; Ratcliff & Rouder, 1998). When assuming a fixed boundary, one assumes the evidence accumulates until a threshold amount of evidence $a$ has been reached. The model typically assumes that the amount of evidence required to terminate the integration process is symmetric about zero, so that the threshold amount of evidence for one alternative is $a$ and the threshold amount of evidence for the other alternative is $-a$. Although the DDM is primarily designed to capture data from a two-alternative forced choice task, extensions to multiple alternatives are possible (see Leite & Ratcliff, 2010; Diederich & Oswald, 2014).

The threshold $a$ serves as a parameter to be estimated from the data. When assuming a fixed boundary, $a$ remains at a constant value throughout time. In other words, under this regime, the decision policy in the model is time invariant. While many have derived analytic expressions for the choice and response time from the fixed boundary version of the DDM (Feller, 1968; Tuerlinckx, 2004; Navarro & Fuss, 2009), because analytic expressions do not yet exist for the collapsing bound version under investigation, we do not discuss these efforts here.²

Collapsing boundaries

Rather than assuming that the amount of evidence required to make a decision remains fixed across time, models that impose a collapsing boundary assume that the amount of evidence needed to make a decision depends on the time that has elapsed. These collapsing boundary models are viewed as extensions of the simple fixed bound version of the DDM discussed above, but feature decisions boundaries whose collapse functions are dictated by another set of model parameters. With these additional parameters, collapsing bounds models can explain a variety of data that traditional fixed bounds models cannot, namely the neurophysiological and decision-making behavior of primates (e.g., Ditterich, 2006a; Kiani & Shadlen, 2009; Shadlen & Kiani, 2013). Additionally, researchers have found that adopting a collapsing decision boundary is optimal in situations where the reliability of the source of evidence is unknown (Shadlen and Kiani, 2013), when there is an effort cost of deliberation time (Busemeyer & Rapoport, 1988; Drugowitsch et al., 2012; Rapoport & Burkheimer, 1971), or when one is attempting to maximize reward after withholding a response for a pre-specified amount of time (e.g., Malhotra et al., 2017; Thura et al., 2012).

One conventionally assumed functional form specifies that the upper boundary $u$ decreases from its initial value $a$ across time $t$, such that

$$ u\left( t\right) = a - \left( 1 - {\exp}\left( -\left( \dfrac{t}{\lambda}\right)^{k}\right)\right)\left( \dfrac{1}{2} a - a^{\prime}\right) $$

(1)

Hawkins et al., (2015), where $a$ is the initial starting point of the boundary, $a^{\prime }$ is the asymptotic boundary setting, and $\lambda$ and $k$ are scaling and shape parameters, similar to the Weibull distribution.

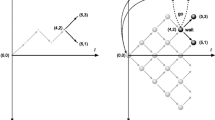
The specific shape of the collapse is determined by the values of the parameters $a^{\prime }$, $\lambda$, and $k$. The asymptotic boundary setting $a^{\prime }$ controls the extent to which the boundaries collapse. Larger values of $a^{\prime }$ lead to a larger separation between the collapsing upper and lower and boundaries (i.e., straighter boundaries), while smaller values of $a^{\prime }$ induce a larger collapse of the decision boundaries. When $a^{\prime } = 0$, the boundaries completely collapse, where the boundaries decrease to a critical value $c$ that is half of their initial starting point $c = a/2$ (Hawkins et al., 2015). The left panel of Fig. 1 illustrates how the parameter $a^{\prime }$ affects the shape of the decision boundary. Here, the scaling parameter is fixed at $\lambda = 1$, and $a^{\prime }$ varies from 0 to 1. When $a^{\prime } = 0$, a complete collapse ensues such that the boundaries collapse to half of the starting boundary value: $c = a/2 = 3/2 = 1.5$. As the value of $a^{\prime }$ increases, the collapse becomes less severe, resembling a fixed bound.

Fig. 1

Effects of parameters on the shape of the collapse. A demonstration of how varying either $a^{\prime }$ (left panel) or the scaling parameter λ (right panel) affects the shape of the boundary collapse

The scaling parameter $\lambda$ determines the stage (i.e., time) of the boundary collapse. As $\lambda$ decreases, the bounds collapse earlier with respect to time. The effect of $\lambda$ on the decision boundary is illustrated in the right panel of Fig. 1. Here, $a^{\prime }$ is held constant at $a^{\prime } = 1$ and $\lambda$ varies from 0.5 to 1.5. When $\lambda = 0.5$, the bounds collapse earlier in the decision process, reaching the asymptotic collapse much earlier than when $\lambda$ is larger.

Finally, the shape parameter $k$ determines the shape of the boundary collapse. Depending on the value of $k$, the boundary could collapse very early in the decision process (early collapse), gradually throughout the decision process (gradual collapse), or later in the decision process (late collapse). For the purposes of this article, the shape parameter was fixed at $k = 3$, which produces a “late” collapse (see Hawkins et al., 2015, for a demonstration).

Theoretical predictions

The shape of the boundary has a major impact on how the diffusion model characterizes the decision-making process. In the time-invariant model, the decision boundaries are fixed, which implies that the amount of accumulated evidence needed to reach a decision remains fixed over time. By contrast, in the time-variant model, the decision boundaries collapse toward zero, meaning that less evidence is required as time increases.

Given these differences, one may wonder whether the models make different predictions for our mixed response signal task. To investigate this, we simulated the two models 10,000 times and recorded important response probabilities. For the time-invariant model, we set the decision threshold to $a = 3$. For the time-variant model, we fixed the starting point of the threshold $a = 3$, the asymptotic boundary parameter $a^{\prime }= 0$, the scaling parameter $\lambda = 0.5$, and the shape parameter $k = 3$. All remaining parameters were equivalent across models: the starting point $z_{0} = 0$, within-trial variability in drift $s = 0.1$, nondecision time $t_{er} = 10$ (in milliseconds), between-trial variability in nondecision time to $s_{\tau }= 0$, between-trial variability in starting point to $s_{0} = 5$, and between-trial variability in drift to $\eta = 0.2$. In line with our mixed response signal task, we examined five different interrogation times: 0.1, 0.3, 0.5, 0.7, and 0.9 s. We also examined three different coherencies: 0, 0.25, and 0.50%. All parameters were chosen to highlight the potential differences in predictions between the two models.

Figure 2 shows the response probabilities for important statistics in our mixed response signal task: 1) the probability $p_{1}$ of making a right response prior to the cue disappearing; 2) the probability $p_{2}$ of making a left response prior to the cue disappearing; 3) the probability $p_{3}$ of making a left response after the cue disappears; and 4) the probability $p_{4}$ of making a right response after the cue disappears. The time-variant model is illustrated as the lines with “X”s, whereas the time-invariant model is illustrated as the lines with open circles. The three coherencies are illustrated as black (0%), red (0.25%), and blue (0.50%) lines. The top left panel shows each model’s predictions for the probability of responding prior to the go cue for each interrogation time. Both models make similar predictions for the first interrogation time, but as time increases, the predictions diverge such that the time-variant model predicts a larger probability of early responding (i.e., prior to the disappearance of the stimulus). As one might predict from the collapsing decision threshold in the time-variant models, the probability of an early response increases by virtue of the decreased need for more evidence with increases in time. Furthermore, the degree of separation is modulated by the strength of coherence for this metric. Namely, at low coherencies, the differences in the models’ predictions are larger than when the coherencies are high.

Fig. 2

Differences in response probabilities. The time-invariant and time-variant models make different predictions for important response probabilities in the mixed task. The top left panel shows that the time-variant model predicts a larger probability of an “early” response (i.e., a response made prior to the disappearance of the stimulus). The top right panel shows the probability of a correct response. The bottom panels show the probability of a correct response, conditional on whether the response was made either prior to (left panel) or after the go cue (right panel). Predictions for the time-variant and time-invariant models are shown as lines with either open circles or “X” symbols, respectively. The color of each pair of lines illustrates differences in the strength of motion coherence: 0% (black), 0.25% (red), and 0.50% (blue)

The top right panel of Fig. 2 shows the probability of a correct response, marginalized over whether the response was made prior to or following the go cue. Here, the top right panel shows that the response probabilities are virtually indistinguishable across the fixed and collapsing bound models. These marginal probabilities are what have been used previously to constrain and compare models of evidence accumulation (Usher and McClelland, 2001; Ratcliff, 2006).

The bottom panel of Fig. 2 shows the probabilities from the top right panel separated by whether the response was made prior to (left panel) or after (right panel) the go cue. These probabilities (in addition to the top left panel) are what make the mixed response signal paradigm unique compared to other interrogation paradigms, as they eliminate the confound between processes that terminate prior to and after the go cue. In the left panel, nearly all model predictions are indistinguishable, with the exception of the 0.25% coherency in the longer delays. Here, the fixed boundary allows for higher accuracy to be achieved relative to the collapsing boundary due to increased stimulus integration. By contrast, the right panel shows large differences between the two models for the probability of a correct response, given that an observer waits for the go cue. Namely, as the coherency increases, the collapsing bound model predicts a substantial decline in accuracy as time increases, relative to the fixed bound model. These differences are most strongly influenced by the relative differences in the amount of integration time.³

The purpose of the simulation above is to show that the mixed response signal paradigm, along with a coherence manipulation, can create differences in the model predictions. Figure 2 reveals that, by allowing subjects to respond early, the models can be discriminated more strongly by virtue of making the response (top left) or the accuracy of those responses conditional on whether a response was made prior to (bottom left) or after (bottom right) the go cue.

By themselves, the four qualitative predictions in Fig. 2 will not be useful in discriminating between the time-invariant and time-variant models when analyzed independently, but rather, they should be used in conjunction to aid in discrimination. For example, the top left panel of Fig. 2 shows discriminability among the models for low coherence conditions, whereas the bottom right panel shows discriminability among the models for high coherence conditions. Hence, the experimental design will play a crucial role in the model comparison analyses we report below (Myung & Pitt, 1997, 2002, 2009). It should be noted that either of the models can adjust other parameters to compensate for predictions that are not supported by the data. For example, the time-invariant model can easily produce increases in the probability of early responses (i.e., the left panel of Fig. 2) by increasing the between-trial drift variability term. Increases in the between-trial drift variability term cause increases in the variance of the state of sensory evidence, and in the limit, the between-trial drift variability term has the largest impact on how the variance increases with time (see Supplementary Materials). When assuming the presence of a bound, the end result is an increase in (early) terminations that also leads to a decrease in accuracy, on average (e.g., see the top right and bottom right panels of Fig. 2). The question is whether the adjustments made by either model produce deficiencies in other aspects of the data. Our experiment was designed to capture these model adjustments, while providing enough constraint to detect said deficiencies.

Model variants

To test the relative merits of collapsing and fixed boundaries, we created 16 different variants by allowing different combinations of between-trial sources of variability and collapsing bound parameters. As a guide, Table 1 provides a list of all model parameters. For simplicity, we can divide these 16 models into four classes. Class 1 (Models 1-4) consists of four variants assuming fixed boundaries that differ by which sources of between-trial variability are allowed to be estimated. Classes 2, 3, and 4 are time-variant models that simply allow different combinations of the collapsing bound parameters to be freely estimated. All models freely estimate the mean of the nondecision time parameter $\tau _{er}$, the between-trial variability in nondecision time $S_{\tau }$, an initial threshold $a$, the mean of the starting point $z_{0}$, and coherence scaling parameter $v$. The response criterion $c(t)=\xi$, which was used to determine a rightward or leftward response should a response not be made prior to the stimulus being removed from the screen, was fixed at $\xi = 0$. The within-trial variability in drift was fixed at $s = 0.1$ for identifiability purposes. We now discuss the remaining specifications intrinsic to each model variant within each class.

Table 1 Diffusion model parameters. Notation of the parameters used throughout this article, along with a description of their functionality

Class 1 is composed of four models that systematically fix and free the between-trial variability in starting point parameter $S_{0}$ and the between-trial variability in drift rate $\eta$. Specifically, Model 1 assumes that both of these terms are fixed to be zero (i.e., $S_{0}=\eta = 0$), Model 2 allows $\eta$ to be freely estimated (i.e., $S_{0}= 0$), Model 3 allows $S_{0}$ to be freely estimated (i.e., $\eta = 0$), and Model 4 allows both model parameters to be freely estimated.

Classes 2 (Models 5–8), 3 (Models 9–12), and 4 (Models 13–16) are derivatives of the four models comprising Class 1, but systematically fix and free the asymptotic boundary setting $a^{\prime }$ and the scaling parameter $\lambda$. For all three of these classes, we set the shape parameter $k = 3$ to reduce both the complexity of the time-variant models and the number of potential model variants. Class 2 freely estimates $a^{\prime }$ but fixes $\lambda = 1$. Class 3 freely estimates $\lambda$, but fixes $a^{\prime }= 0$. Finally, Class 4 freely estimates both $a^{\prime }$ and $\lambda$. The arrangement of parameters featured in each of the 16 variants can be found in the Supplementary Materials.

Methods

In this section, we describe our perceptual decision-making task. As discussed in the introduction, our strategy was to use a mixture of interrogation and free response paradigms so that the amount of stimulus processing time could be treated as an independent variable in our experiment. In addition, the levels of processing time were crossed with the coherency of the dot motion, creating a fully factorial design of strength and duration of evidence.

Subjects

Fourteen healthy subjects were recruited from Ohio State University. All subjects provided written consent in accordance with the university’s institutional review board and received partial course credit for their time. With the exception of two subjects, all subjects completed the full design consisting of 650 trials. Of the two who failed to complete the study, one only completed 543 of the 650 trials due to scheduling conflicts, and the other abandoned the task at trial 220 of 650. However, both subjects’ data were included in all analyses.

Stimuli and equipment

The random dot motion task (see Newsome and Pare, 1988) was created using a custom program named the State Machine Interface Library for Experiments (SMILE; https://github.com/compmem/smile) , which is an open-source, Python-based experiment building library. Subjects completed the task on a desktop computer with a 15- inch display, running at 60 Hz, in a cubicle within view of an experimenter.

Design

The mixed response signal task used a $5 \times 5$ (motion strength $\times$ interrogation time) within-subject factorial design. The levels of motion coherency were 0, 5, 15, 25, or 35% in either the rightward or leftward direction. The condition of 0% coherency was used as a control condition to enhance our ability to infer perceptual biases that might occur for each subject. The interrogation time could occur at any of the following times: 100, 300, 500, 700, or 900 ms. The interrogation times serve as the control for the stimulus duration. That is, the stimuli were presented for a certain number of milliseconds, after which time the dots were removed from the display. Subjects were trained to treat the removal of the dots as a “go cue” such that a response should be initiated. However, subjects were also instructed that they could initiate a response while the dots were still on the screen. The full factorial design of our task is displayed in Table 2.

Table 2 Experimental design. Columns represent the levels of stimulus durations (i.e., interrogation times), whereas rows represent the levels of coherency. In each block, each stimulus duration and motion strength pair was randomly selected and presented twice

On each trial, subjects were presented with clouds of dots constructed using one of the motion strength and interrogation time pairs listed in Table 2, and they were required to make a direction of motion (i.e., either left or right) decision based on which direction most of the dots were moving by pressing either the “D” key with their left hand or the “K” key with their right hand.

Subjects completed one practice block before completing 13 additional blocks, consisting of 50 trials per block. This resulted in 650 total trials. On each block, each motion-strength-interrogation-pair in Table 2 was randomly presented once for rightward moving dots and once for leftward moving dots.

Procedure

After obtaining informed consent, subjects sat in front of the computer and were provided with brief instructions by the experimenter. These instructions informed the subject that they would be completing several blocks of a random dot motion task, and that the dot stimuli would only be on the screen for a short period of time before being removed. After explaining the task, the experimenter explicitly stressed that while the dots would be removed after a short period of time, the subject did not have to wait for the dots to disappear and could respond at any time. Subjects were informed that they could respond as soon as they were aware of which direction the dots were moving, and that they could respond prior to the dots leaving the screen if they so chose.

After the instruction period, the experimenter started the program and left the room. Each block began with an instruction screen that provided a description of the task, the key mapping, and an illustration of leftward and rightward moving dots. Once subjects felt they were ready to begin the task, they pressed the ENTER key and the task began. Each trial began with the presentation of a fixation cross that remained on screen for 100 ms. Then, a cloud of randomly moving dots were presented to the subject for a prespecified amount of time, and the subjects were asked to make a direction decision. Again, subjects were informed prior to beginning the experiment that they were free to respond as soon as they felt they knew the answer. The motion strength and interrogation times were randomly chosen and counterbalanced across trials. Once a response was made, feedback was presented for 100 ms in the form of a green checkmark for correct answers or a red $X$ for errors. Finally, the fixation cross reappeared, denoting a new trial. Subjects were also given feedback in the form of “too fast” or “too slow” if they responded prior to 100 ms after stimulus onset or after 2500 ms post interrogation time, respectively.

Fitting the models

Figure 3 shows the basic strategy we used for fitting each of the 16 models to data by demonstrating how the data were organized for a given stimulus coherency $i$ and duration time $j$ (see Table 2). For each cell in the factorial design, we organized the data $D_{i,j}=\{n_{1},n_{2},n_{3},n_{4}\}$ based on the number of times four unique events occurred: a rightward (n₁) or leftward (n₂) response prior to the dots disappearing (i.e., prior to the interrogation time); and a rightward (n₃) or leftward (n₄) response after the dots disappeared (i.e., after the interrogation time), where $\sum _{k} n_{k}=N_{i,j}$. From a modeling perspective, this distinction is important because it separates out two different types of accumulation: in one type, enough evidence was acquired prior to an interrogation time, whereas in another, introspection is necessary to determine the state of evidence acquired conditional on the stimulus duration. By factorially manipulating the stimulus coherency with stimulus duration, we can decipher how coherency interacts with duration and provide greater constraints on the models.

Fig. 3

Model fitting strategy. For a given stimulus coherence and duration (i.e., black vertical line), the figure shows how the data (left panel) and model simulations (right panel) were organized to evaluate the suitability of a given model parameter. The left panel shows how the data were discretized into four contingencies: rightward (n₁) or leftward (n₂) response prior to the cue disappearing, and a rightward (n₃) or leftward (n₄) response after the interrogation time. The right side illustrates an analogous discretization of the model simulations. The red horizontal line represents the right/left criterion. Note that in the model simulations, the criterion is only realized if a bound is not hit prior to the disappearance of the cue

To fit our models to data, we require a method of assessing the relative accuracy of a model’s predictions relative to the data contingencies illustrated in the left panel of Fig. 3. Given that some of the models under investigation in this article do not yet have analytic likelihood functions, we can instead simulate the model many times to obtain an approximation of how likely the data in the left panel of Fig. 3 are under a given set of model parameters (i.e., the likelihood function). Various methods for using model simulations to approximate the likelihood function have been developed and shown to be accurate in several different modeling applications (e.g., Heathcote, Brown, & Mewhort, 2002; Turner & Van Zandt, 2012, 2014; Turner & Sederberg, 2012, 2014; Turner, Dennis, & Van Zandt, 2013; Turner, Schley, Muller, & Tsetsos, 2018; Hawkins et al., 2015; Palestro et al., 2018). The right panel of Fig. 3 shows simulated trajectories from one of the models for a given set of model parameters. Here, we simulated the model many times for a fixed amount of time (i.e., the longest interrogation time in our experiment), and then we analyzed the accumulation paths to separate the event contingencies in an analogous way to the data arrangement in the left panel.

To separate the event contingencies, we simply track the state of each accumulation path. Letting $x\left (t\right )$ denote a given accumulation path, the first contingency is whether a bound was hit prior to the stimulus disappearance. If we let $a(t)$ denote the state of the boundary at a given time $t$ and $t^{*}$ denote the interrogation time, we can define the first point $t_{0}$ such that a boundary was crossed as

$$t_{0} = \min \left[ t \in (0,\infty): |x(t)|\ge a(t) \right]. $$

Because we cannot realistically simulate the model for an infinite amount of time, it is possible that the state $x(t)$ never crosses the boundary $a(t)$. In this case, we set $t_{0}=t^{*}$ to indicate that a boundary was not hit prior to the stimulus disappearing.⁴ Using the boundary crossing time $t_{0}$ and the boundary symmetry assumed within the DDM (i.e., the boundaries are symmetrical about 0), we can define the probability of making a right (p₁) or left (p₂) response prior to the stimulus disappearing as

$$\begin{array}{@{}rcl@{}} p_{1}&=&p\left( t_{0} < t^{*} ~\cap~ x(t=t_{0})>0 \right) \text{, and} \\ p_{2}&=&p\left( t_{0} < t^{*} ~\cap~ x(t=t_{0})<0 \right), \end{array} $$

respectively. The second contingency is whether a decision was made after the stimulus disappeared. For simplicity, we assume that when the stimulus disappears, no more information can be processed, although there are many other proposals for post-stimulus processing (Pleskac & Busemeyer, 2010; Moran, 2015). Because we assume that no more information can be processed, to form estimates of the final contingencies, we examine the states of evidence at the interrogation time $t^{*}$. To make a left/right decision, we assume the observer evaluates the state of evidence at the interrogation time relative to a criterion parameter $\xi$. If the state of evidence is greater than the criterion, a rightward decision is made, whereas if the state of evidence is less than the criterion, a leftward decision is made. Formally, the probabilities of leftward (p₃) and rightward (p₄) responses following an interrogation time are

$$\begin{array}{@{}rcl@{}} p_{3}&=&p\left( t_{0} \ge t^{*} ~\cap~ x(t=t^{*})>\xi \right) \text{, and} \\ p_{4}&=&p\left( t_{0} \ge t^{*} ~\cap~ x(t=t^{*})<\xi \right), \end{array} $$

respectively. Together, the above decision rules enforce the constraint $\sum _{k} p_{k} = 1$. Each event probability $p_{k}$ is shown in the right panel of Fig. 3, and their relationship to important probabilities in the mixed response signal task is shown in Fig. 2. The red horizontal line represents the criterion parameter $\xi$, but it should be noted that the criterion only plays a role when decisions are made after the stimulus has disappeared. Similarly, the response threshold $a(t)$, illustrated as the boundary box surrounding the trajectories, only plays a role when decisions are made prior to the disappearance of the stimuli.

Once each of the event probabilities have been obtained, we need to evaluate how closely the distribution of event probabilities match the observed data. One way to do this is through a simplified version of the probability density approximation (PDA; Turner & Sederberg, 2014) method for data of discrete type. Here, we conceive the data observations as a multinomial draw with probabilities dictated by the model simulations. For a given stimulus coherency $i$ and viewing duration $j$, we can evaluate the probability of observing the data $D_{i,j}$ given a set of model parameter $\theta$ as

$$\pi(D_{i,j} | \theta) = \dfrac{N!}{n_{1}!,n_{2}!,n_{3}!,n_{4}!} p_{1}^{n_{1}} p_{2}^{n_{2}} p_{3}^{n_{3}} p_{4}^{n_{4}}, $$

where

$$(p_{1}, p_{2}, p_{3}, p_{4}) \sim \text{Model}(\theta). $$

The notation $\text {Model}(\theta )$ denotes the model simulation process and path analysis described above, producing the predicted model probabilities $p_{k}$. Note that to simulate the model, design information such as stimulus coherency and viewing duration are used explicitly in the model to generate the paths and produce each $p_{k}$.

For computational convenience, we simulated the model 1000 times for a given parameter proposal $\theta$ using the longest viewing duration in our experiment (i.e., 900 ms). We then calculated each of the $p_{k}$s by analyzing the trajectories for each viewing duration by setting $t^{*}$ accordingly in the process described above. To form an approximation of the likelihood function $\mathcal {L}(D|\theta )$ of the data $D$ given a parameter proposal $\theta$, we need only calculate the distribution of $p$ relative to the distribution of $n$ across all stimulus coherencies and viewing durations using the following equation:

$$\mathcal{L}(\theta | D) = \prod_{i} \prod_{j} \pi \left( D_{i,j} | \theta \right). $$

To generate the parameter proposals $\theta$, we used a simulation-based method know as approximate Bayesian computation with differential evolution (ABCDE; Turner & Sederberg, 2012). Specifically, we used the “burn in” mode of the ABCDE algorithm, as we were only interested in maximizing the approximate posterior density (i.e., the approximate maximum a posteriori (MAP) estimate), rather than sampling full posterior distributions. For each model, we implemented this sampler with 32 chains for 300 iterations. The in-group migration probability was set to 0.15, and the jump scaling factor was set to $b = 0.001$.

Prior specification

With a suitable approximation of the likelihood function in hand, the final step in estimating the joint posterior distribution is to specify prior distributions for each of the model parameters. We specified the following priors:

$$\begin{array}{@{}rcl@{}} \log(v), log(z_{0}), \log(t_{er}), \log(S_{t}), \log(\eta), \log(a^{\prime}), \log(\lambda) &\sim& \mathcal{N}\left( 0,1\right) \\ \log(a) &\sim& \mathcal{N}\left( 1,0.5\right) \\ \log(S_{0}) &\sim& \mathcal{N}\left( 0.5,1\right). \end{array} $$

While these priors may seem informative, as most of the parameters are on the log scale, the constraint is justified as once these variables are transformed, the range of the prior is only mildly informative. For example, the 95% credible range of a log normal prior with mean 0 and standard deviation of 1 is $(0.14, 7.13)$.

Model comparison

To compare the relative fit of the 16 models, we computed three different metrics: the Bayesian information criterion (BIC; Schwarz, 1978), the approximated posterior model probabilities (Wasserman, 2000), and an approximation to the Bayes factor. The BIC is computed for each model using the equation

$$ \text{BIC} = - 2{\log} \left( L\left( \hat{\theta}|D\right)\right) + {\log}\left( N\right)p, $$

(2)

where $L\left (\hat {\theta }|D\right )$ represents the log of the posterior density at the parameter value that maximized it (i.e., the maximum a posteriori (MAP) estimate), $p$ represents the number of parameters for a given model, and $N$ is the number of data points (i.e., trials) for a given subject. The BIC penalizes models based on complexity, with models of higher complexity (i.e., models with more parameters) receiving a stronger penalty than models of lower complexity. As such, the inclusion of additional parameters must substantially improve the fit to the data to overcome the penalty incurred for adding them.

We can use the BIC values calculated for each candidate model to approximate each model’s posterior model probability relative to the other 15 models. This approximation, as given by Wasserman (2000) is as follows:

$$ P_{BIC}\left( M_{i} | Data\right) = \dfrac{{\exp}\left( -\dfrac{1}{2}\text{BIC}\left( M_{i}\right)\right)}{\sum_{j = 1}^{m}{\exp}\left( -\dfrac{1}{2}\text{BIC}\left( M_{j}\right)\right)}. $$

(3)

We can calculate the Bayes factor $BF_{q,r}$ between two model candidates $M_{q}$ and $M_{r}$ using

$$ BF_{q,r}=\dfrac{p(D|M_{q})}{p(D|M_{r})}, $$

(4)

where $p\left (D|M_{i}\right )$ is the marginal likelihood of the data $D$ under a model $M_{i}$. While simple in theory, to calculate the Bayes factor, it is preferred that the likelihood function for each candidate model be analytically tractable (see Gelman et al., 2004; Liu and Aitkin, 2008 for greater detail). Unfortunately, while the likelihood function for the time-invariant diffusion decision model has been analytically derived (Feller, 1968; Ratcliff, 1978; Tuerlinckx, 2004; Navarro & Fuss, 2009; Voss, Voss, & Lerche, 2015), the collapsing decision boundary under consideration complicates these equations enough to render the likelihood intractable. As the likelihoods must be approximated, so too must the marginal likelihoods in Eq. 4.

To approximate the Bayes factor, we can use a method suggested in Kass and Raftery (1995), which estimates the Bayes factor by comparing the BIC value calculated for each candidate model. Kass and Raftery (1995) demonstrated that the difference between BIC values for candidate Models $q$ and $r$ asymptotically approximates $-2{\log }\left (BF_{qr}\right )$ as $N$ approaches $\infty$. Hence, we can approximate the Bayes factor in Eq. 4 by using the BIC values from Eq. 2:

$$ BF_{q,r} \approx \exp \left[-\dfrac{1}{2}\left( \text{BIC}_{q} - \text{BIC}_{r} \right) \right], $$

(5)

where $\text {BIC}_{i}$ denotes the BIC score for Model $i$.

Results

We present the results in three stages. First, we show the raw behavioral data to ensure that our task manipulations were effective. Second, we provide details of the model comparison by reporting the Bayesian Information Criterion (BIC; Schwarz, 1978), an approximation of each model’s posterior model probability (Wasserman, 2000), and an approximation to the Bayes factor (Kass & Raftery, 1995) and a comparison to observed data. Here, we also investigate the role that practice effects might have played in influencing our model fitting results. Finally, we provide some insight into the model comparison results by examining the representations inferred from the model fits.

Raw behavioral data

To explore the effectiveness of our task manipulation, we first examined the choice response time distributions as a function of the levels of our independent variables. Recall that we explicitly manipulated the length of time that a given stimulus was presented and the strength of motion coherence. Our hypothesis was that each of these variables should affect both the accuracy and the response time associated with each decision, as they both uniquely contribute to the amount of evidence for a choice. Namely, the strength of motion coherence should contribute positively to the quality of the decision, where increases in motion coherence should increase accuracy and decrease response times. Interrogation times should also contribute positively to the quality of the decision, where increases in the length of the viewing times should increase accuracy. The interaction between interrogation times and response times is complicated in our task, as subjects had the ability to respond before the stimulus was removed from the screen. However, a “premature” (i.e., relative to the interrogation time) response does give us information about the perceived strength of evidence as well as the amount of evidence required by an observer to make a choice. As we will discuss later, these features of the data were helpful in evaluating performance among the models.

Figure 4 shows the choice response time distributions for each level of the two independent variables in our task. The panels of Fig. 4 are organized by the time at which subjects were interrogated (columns) and the strength of motion coherency (rows). Within each panel, response times associated with correct responses are shown on the positive axis, whereas response times associated with incorrect responses are shown on the negative axis. As a reference, a response time of zero seconds is illustrated as a red vertical line, and the interrogation times (also indicated by the column) are shown as the blue vertical lines. Response times were trimmed to be greater than 100 ms and less than 4000 ms, resulting in a removal of approximately 0.7% of trials. Again, as the response times depend to some extent on the interrogation times, this particular feature of our data is difficult to visualize in Fig. 4. Within each panel, if response times appear between the red vertical line and the blue vertical line (on either axis), then the choice was made prior to the stimulus disappearing. By contrast, if a response time is larger than the interrogation times (i.e., blue vertical lines), then a response was made after the stimulus disappeared.

Fig. 4

Choice response time distributions. Each panel shows the choice response time distributions from our experiment, collapsed across subjects, where response times associated with correct responses are shown on the positive axis and incorrect responses on the negative axis. The panels are organized by the time at which subjects were interrogated (columns) and strength of motion coherency (rows). As a reference, a response time of zero seconds is illustrated as the red vertical line, and the level of interrogation time is illustrated as the blue vertical line. The statistic in the upper right corner of each panel provides the probability that a response was made prior to the stimulus disappearing

Figure 4 reveals a few interesting interactions between the independent and dependent variables. To get a sense of accuracy, we must compare the relative heights of the two response time distributions within a panel, where a larger density of the response time distribution on the positive axis indicates greater accuracy. Comparing across the rows, for a given interrogation time, accuracy increases with increasing coherency, and the response times tend to decrease. Together, these results suggest that coherency had a large impact on the strength of evidence for the correct choice. Comparing across columns, for a given coherency, accuracy increases with increasing interrogation times, suggesting that with longer viewing durations, a stronger overall strength of evidence could be appreciated by the subjects. The interrogation times do not seem to have a direct impact on the response times, although as interrogation times increased, more responses were made prior to the stimulus disappearing. Also, some distributions do appear to be bimodal, especially at longer interrogation times. One potential explanation for this bimodality is that longer interrogation times induce different response modalities across subjects: some subjects tend to respond prior to the go cue (creating one mode), whereas others prefer to wait until the go cue before initiating a response, producing the bimodal shape.

The left panel of Fig. 5 displays the accuracy data in another way, where here the accuracy for each experimental cell was calculated by collapsing over response time. The accuracy (y-axis) is shown as a bar plot for each interrogation time (x-axis) and for each coherency (columns). In the 0% coherency condition, accuracy centers around chance responding (i.e., 0.50). As coherency increases, Fig. 5 shows that the proportion of correct responses increases for each level of interrogation time. For a given coherency, the accuracy of the responses tends to increase with increases in the interrogation time. The right panel of Fig. 5 shows the accuracy data in the same way, but separated by whether the response was made prior to (i.e., top panel) or after (i.e., bottom panel) the stimulus disappeared. Here, we see that when a response was executed prior to the cue disappearing, it tended to be modulated by the interrogation time, where longer interrogation times tend to increase the accuracy. However, this trend is not necessarily observed when responses are made after the cue disappeared (i.e., bottom panel).

Fig. 5

Accuracy across independent variables. The left panel shows the accuracy (y-axis) as a bar plot for each interrogation time (x-axis), and for each coherency (panels), collapsed across response times. The right panel shows the same information as in the left panel, but separated based on whether the response was made prior to (top panel) or after (bottom panel) the stimulus disappeared. Error bars represent the standard error in the proportion correct

Taken together, Figs. 4 and 5 suggest that the data from the mixed response signal task match our expectations about how each independent variable should interact with both accuracy and response time.

Model comparison

The most important aspect of our results is the comparison in fit statistics across models. We used the approach detailed in Section 2 to fit each of the 16 model variants to our data. We fit each subject independently and obtained a single maximum a posteriori (MAP) estimate that maximized the posterior density. The MAP estimate was then used to evaluate the log likelihood obtained, so that the Bayesian predictive information (BIC; Schwarz, 1978) could be calculated.

Figure 6 shows the resulting BIC values obtained by fitting each model (i.e., rows) to each subject’s data (i.e., columns 1-14). For visual purposes and because the BIC values cannot be interpreted in an absolute sense, we z-scored the BICs (i.e., the zBIC) across models for a given subject so that model performance could be assessed more easily. To do this, we subtracted each BIC value in a given column from the mean BIC value in that column and divided by the standard deviation of the BIC values within that column. The final column shows the performance of each model by averaging the BICs across subjects. Although these group values do not technically reflect how well each model fit the entire set of data, they provide some information about the average performance across subjects. Each model performance statistic is color coded according to the legend on the right hand side; for the zBIC (and the BIC), lower values reflect better model performance, which are illustrated with cooler (i.e., bluish) colors.

Fig. 6

Model comparison. Each box illustrates the z-scored BIC value obtained for each subject (columns) and model (rows) combination, color coded according to the legend on the right-hand side. Lower BIC values (i.e., cooler colors) correspond to better model performance. The panel on the left summarizes the models investigated here, where the columns correspond to the model number and the specific model parameters that were either fixed (filled circle), free to vary (empty circle) or not applicable (an “x” symbol). For convenience, the models were also grouped into classes: time-invariant (Models 1-4; red), time-variant models with $a^{\prime }$ free (Models 5-8; blue), time-variant models with λ free (Models 9-12; green), and time-variant models with both $a^{\prime }$ and λ free (Models 13-16; purple)

The left panel of Fig. 6 provides a schematic of the various models investigated here. Parameters are represented as nodes in each column, where parameters that were freely estimated are empty, parameters that were fixed are solid, and parameters that are not applicable are shown as “x”s. From left to right, the columns are the model numbers, between-trial variability in starting point $s_{0}$, between-trial variability in drift $\eta$, the asymptotic boundary setting $a^{\prime }$, and the scaling parameter $\lambda$. For ease of discussion, the models were grouped into four classes mentioned in Section 2: Models 1-4 (Class 1; red) are the time-invariant models, Models 5-8 (Class 2; blue) are the time-variant models with $a^{\prime }$ free and $\lambda$ fixed, Models 9-12 (Class 3; green) are the time-variant models with $a^{\prime }$ fixed and $\lambda$ free, and Models 13-16 (Class 4; purple) are the time-variant models with both $a^{\prime }$ and $\lambda$ free. A similar analysis using the approximate posterior model probabilities as given by Wasserman (2000) can be found in the Supplementary Materials, along with the raw model fit statistics.

Figure 6 shows that, across subjects (i.e., going down the group column in Fig. 6), lower zBIC values are obtained with time-variant models, specifically the Class 3 models that allow $\lambda$ to be free. The Class 4 models also perform well, presumably because $\lambda$ is free, and the penalty incurred by freeing $a^{\prime }$ is not enough to hinder the performance of these models. Of course, for some subjects this is not the case, such as with Subject 12 and 13, who are poorly fit by Class 4 models, but are still fit well by Class 3 models. In this case, the penalty term for freeing $a^{\prime }$ was enough to rule out Class 4 models. The clear worst-performing class is Class 1, with the worst performer within this class being the one that is most constrained (i.e., having only nondecision time variability).

Within a class, it is more difficult to say which parameters should be free to vary, as some inconsistencies emerge. For example, in Class 2, having between-trial variability in starting point performs about as well as having between-trial variability in drift or allowing both to vary. However, in Class 3, having either one of these parameters free to vary performs better than having neither one free or both free. For Class 4, having between-trial variability in drift is better than every other combination.

Model fit to observed data

In addition to comparing fit statistics across models, we can also evaluate how well each model fit the data by comparing the predictions of the model against the observed data. To do so, we simulated the best-fitting model from each class (Models 4, 7, 11, and 14) 10,000 times using the best-fitting model parameters (i.e., the MAP estimates) for each subject. After simulating, we calculated the probability of each event contingency using the same method as described in Section 2 and then averaged these probabilities across subjects. Finally, using these probabilities, we calculated the proportion correct for each condition in our task for three different response types—all responses, responses before the cue (i.e., before the dots were taken away), and responses after the cue (i.e., after the dots were taken away)—and plotted the model predictions against the data in Fig. 7.

Fig. 7

Average model predictions versus observed data. Each panel plots the model predictions from the best-fitting model from each class against the observed data, collapsed across time and coherency

Comparing across all four panels, Fig. 7 suggests that while each model appears to make similar predictions, Model 4 (includes both sources of variability) and Model 14 (includes both sources of variability and freely estimates $a^{\prime }$ and $\lambda$) over-predicted the accuracy on some occasions relative to Model 7 (includes between-trial variability in the starting point and freely estimates $a^{\prime }$) and Model 11 (includes between-trial variability in starting point and freely estimates $\lambda$). The correlations between the predictions and the data support this notion: Model 7, Model 11, and Model 14 had the highest correlations (r = 0.662, $\textit {r} = 0.649$, and $\textit {r} = 0.616$, respectively); while Model 4 had the lowest correlation (r = 0.561). These correlations suggest a different rank ordering than the BIC statistics displayed in Fig. 6. However, the general pattern is consistent: time-variant models account for the observed data better than the time-invariant model. The Supplementary Materials provide model comparison plots against the raw data, separated by condition and coherency.

Approximating the Bayes factor

Once each BIC value had been obtained (see Fig. 6), we used Eq. 4 to approximate the Bayes factor (Kass and Raftery, 1995). Rather than comparing all 16 models, Fig. 8 shows the Bayes factor for the best-fitting collapsing bound model across subjects (Model 11) relative to the best-fitting fixed bound model across subjects (Model 4). Figure 8 shows the approximated Bayes factor for each subject, sorted according to the amount of evidence provided for the collapsing bound variant. The Bayes factor is shown on the log scale, so subjects near zero are best described by neither model preferentially. For 11 out of the 14 subjects, the approximated Bayes factor for the collapsing bound model is larger than 100, indicating strong preference. The approximated Bayes factor scores for each subject can be found in the Supplementary Materials.

Fig. 8

Bayes factor approximation by subject. Each point represents the approximated Bayes factor comparing the overall best-fitting time-invariant model (Model 4) to the overall best-fitting time-variant model (Model 11) for each subject

Practice

In plotting the aggregated response time as a function of experimental block, we noticed a substantial decrease in the response times through blocks (see the Supplementary Materials for additional information). While this general pattern of decreasing response times with practice is ubiquitous (sometimes referred to as the “power law of practice” ; Logan, 1988), because practice effects have been put forward as an explanation for differences in decision policies across species (e.g., Hawkins et al., 2015), we performed an additional analysis to ensure the generality of our results.

To determine if practice unduly biased subjects to collapse their decision thresholds, we split the data in half and fit Models 4, 7, 11, and 14 (i.e., the best-fitting model from each class) to both halves independently, using the same methodology as in Section 2. If practice does bias each subject’s strategy, we might expect the time-invariant model (Model 4) to provide a better fit to the first half of the data and some time-variant model (Models 7, 11, or 14) to provide a better fit to the second half. If practice has little to no impact on strategy, then the time-variant models should provide better fits to both halves of data, relative to the time-invariant model.

Figure 9 displays the BIC values obtained from fitting the four models to each subject’s first (top panel) and second (bottom panel) half data. This figure was constructed in the same manner as Fig. 6, where the BIC values were z-scored across models for a given subject and color coded according to the legend on the right hand side. Again, lower values reflect better model performance and are illustrated as cooler colors while higher values reflect worse performance and are illustrated as warmer colors.

Fig. 9

Model comparison of split data. Each box illustrates the z-scored BIC value obtained for each subject (columns) and model (rows) combination, color coded according to the legend on the right-hand side. Lower BIC values (i.e., bluish colors) correspond to better model performance. The panel on the left summarizes the models investigated here, where the columns correspond to the model number and the specific model parameters that were either fixed (filled circle), free to vary (empty circle) or not applicable (an “x” symbol). The models are color coded according to class: time-invariant (Model 4; red); time-variant with $a^{\prime }$ free (Model 7; blue); time-variant with λ free (Model 11; green); and time-variant models with both $a^{\prime }$ and λ free (Model 14; purple). The top panel shows the model evaluations for the first half of the data (i.e., Blocks 1-8), whereas the bottom panel shows the results for the second half of the data (i.e., Blocks 9-16)

The top panel of Fig. 9 shows the relative fits of each model to the first half of the data. In this panel, Model 7 explains the data from all 14 subjects better than the other three models with Models 11 14, and 4 following in that order. The bottom panel of Fig. 9 shows the relative fits of each model to the second half of data. These fits show much more variability across subjects relative to the first half fits, but here, we observe a pattern of results similar to that of Fig. 6, where Model 11 provided the best fit to most of the subjects. As an additional check (see Supplementary Materials), we performed another model-fit comparison by fitting the same four models to the entire set of data, with the first four problematic blocks removed. Here, we again found that Model 11 provided the best account, with Models 14, 7, and 4 following in that order. Taken together, lower zBIC scores are obtained with time-variant models across subjects and halves, with the time-invariant model (Model 4) being the worst overall performer. These results suggest that the model-fitting results are consistent, regardless of some moderate practice effects in the first four blocks of our data.

Inferred task representations

Thus far, our results suggest that all of our subjects are best accounted for by some variant of a collapsing bound model. However, model fit comparisons such as the ones presented in Figs. 6 and 8 do not tell us much about why one model architecture provides a better fit over another. To investigate this, we can look to the task representations that might have been used by each subject during the task. Examining the inferred task representations has the advantage of projecting several parameter dimensions down into something that is easily visualized, so that we can gain clearer insight into how the various parameters interact with one another.

To illustrate the differences in model fit, Fig. 10 shows two subjects who obtained two different results in the model fitting comparison. The left column shows Subject 6, whose data were best accounted for by the “modern” time-invariant model (Model 4; includes both sources of between-trial variability), whereas the right column shows Subject 8, whose data were best accounted for by its time-variant derivative (Model 16; includes both sources of between-trial variability and freely estimates $a^{\prime }$ and $\lambda$). The top row shows the empirical response time distributions, collapsed across choice and condition information. The middle row shows the inferred task representation used by a fixed bound model, whereas the bottom row shows the inferred task representations used by a collapsing bound model. These subjects were chosen because (1) they yielded different model fitting results, and (2) their general pattern of choice response time distributions were similar. The Supplementary Materials provides similar plots for the remaining 12 subjects.

Fig. 10

Inferred task representations. The columns correspond to two subjects whose data were either fit best by a fixed boundary model (left column), or a collapsing boundary model (right column). The top row shows the empirical response time distribution collapsed across choice and stimulus conditions, the middle row shows the task representation inferred by a fixed boundary model, whereas the bottom row shows the task representation inferred by a collapsing boundary model. The drift rates for each coherency condition are shown, color coded according to the key in the middle right panel

To generate the task representations, we simply recreated plots such as the one presented in Fig. 2 using the MAP estimates obtained during the model fitting process. The relevant MAP estimates for Fig. 10 are the threshold, drift rates, nondecision times, and collapsing bound parameters (i.e., for the bottom row). For the drift rates, we plotted the average trajectory that was inferred from fitting the model to data for each stimulus coherency condition. For Subject 6, Fig. 10 shows that for the time-variant model, the inferred boundary does not collapse until late in the decision-making process (i.e., after most of the drift rate trajectories have crossed the boundary), and the inferred collapse in the bottom panel is minimal, suggesting that the collapse played no role in the model’s ability to account for the data of this subject. As such, the time-invariant model provided a better fit once balancing for the number of parameters.

The right panel of Fig. 10 shows the inferred representations for Subject 8, who was best captured by the time-variant model. In contrast to the left panel, the inferred boundary collapses completely and early in the decision-making process, causing the drift rates to terminate at the collapsing boundary rather than the fixed boundary. For this subject, the interaction of the drift rates and the stage of the collapse allow the collapsing bound model to account for the tail end of the response time distribution slightly better. Across all subjects, the pattern of drift rates interacting with the collapsing bound parameters was a strong predictor in determining which model would ultimately provide the best fit. Namely, when the drift rates of one or more coherency condition hit a boundary during a collapse, the collapsing bound provided the better fit.

Discussion

The classic, time-invariant DDM has proven exemplary in accounting for a variety of empirical data across a number of domains (see Forstmann, Ratcliff, & Wagenmakers, 2015, for a review). Recently, the classic DDM has come under scrutiny with the focal point being the manner in which the model deals with the timing of the choice. In its place, diffusion models with additional mechanisms, such as urgency or collapsing boundaries, have been proposed, and these models have proven effective in accounting for both human and primate data from similar perceptual decision-making tasks (Ditterich, 2006a, b; Kian & Shadlen, 2009; Shadlen & Kiani, 2013). While there is considerable controversy surrounding the nature of the task demands, stimulus used, and even the species of the subject under study, if these mechanisms have proven generally effective in capturing data, they provide an interesting and exciting alternative to a long standing tradition in models instantiating sequential sampling theory.

The purpose of this article was to further investigate how stimulus characteristics interact with task demands. While other reports have been criticized for using stimuli that may inherently bias subjects toward a collapsing bound policy, our task centers on one of the most well-studied stimuli in perceptual decision-making history: the random dot motion task. Starting from a well-agreed-upon stimulus, we asked whether factorially manipulating the strength of coherent motion as well as the length of the stimulus exposure could induce a collapsing boundary policy. The factorial structure of the experiment helped to add constraints on the ensuing model-fitting exercise, but perhaps the strongest constraint was the addition of an “opt-out” policy embedded within the interrogation paradigm. As discussed, the standard version of the interrogation paradigm produces a confound in that decisions terminated via an endogenous stopping rule cannot be separated from decisions that are terminated via an exogenous cue (i.e., the go cue). The opt-out procedure allows us to separate out these two possibilities, allowing for better assessment of how stimulus strength interacts with the decision boundary.

To test our hypothesis, we compared the relative fit of 16 diffusion model variants with fixed and collapsing decision thresholds to data from our modified random dot motion task. We compared each model’s ability to fit data from the mixed response signal task by calculating three different model fit statistics: the Bayesian information criterion (Schwarz, 1978), approximated posterior model probabilities (Wasserman, 2000), and an approximation to the Bayes factor (Kass & Raftery, 1995). The BIC measures suggested that a variant with collapsing decision boundaries was preferred across all 14 subjects. Collapsing across subjects, we found time-variant models that freely estimate the scaling parameter $\lambda$ in the collapsing decision boundary provide the best fits overall. The approximate posterior model probabilities showed similar results (see Supplementary Materials), with time-variant models that freely estimate the scaling parameter $\lambda$ having higher posterior model probabilities across all subjects. The approximated Bayes factor analysis further confirmed this point in that they provided definitive and consistent evidence for time-variant models.

We also compared the fit of the four best-fitting models from each class to data from the mixed response signal task. This comparison further corroborated our results that the time-variant models provide a better fit to the data than the time-invariant model. Taken together, our results suggest that the mechanisms in the time-variant model provide a more viable explanation for the strategies subjects use to complete our mixed response signal task.

Given that we found evidence supporting collapsing boundaries, it seems productive to speculate on the reason for adopting a collapse for our particular task. As other researchers have compared models using time-variant and time-invariant mechanisms (e.g., Ditterich, 2006a; Hawkins et al., 2015; Voskuilen et al., 2016), we can follow some of their rationales in interpreting our results. This section discusses three such rationales: species differences, stimuli differences, and task differences.

Species differences

Much of the support for time-variant models comes from neurophysiological literature exploring the decision-making behavior of primates (e.g., Chuchland, Kiani, & Shadlen, 2008; Hanks, Mazurek, Kiana, Hopp, & Shadlen, 2011) and behavioral literature comparing the relative fits of time-variant and time-invariant models to primate data (e.g., Ditterich, 2006a). In the most detailed comparison to date, Hawkins et al., (2015) tested whether human and primate data were best captured by time-variant or time-invariant models and found that the majority of the primate data sets were best accounted for by time-variant models. However, when applying the same set of models to human data, Hawkins et al., (2015) found that the majority of human data sets were best accounted for by time-invariant models.

One of the major explanations of differences in results across species was the effect of practice. Hawkins et al., (2015) explained that non-human primates are subject to many practice sessions, often on the order of months or years. Due to this extensive practice, it is of course reasonable that the distributions of response times change. While the shapes of our subject’s response time distributions do not appear Gaussian (see Fig. 10 as an example), an analysis of the mean and standard deviation of the response times across each experimental block in our task (see Supplementary Materials) identified that some practice effects may have been present in our data.

However, after splitting the data in half and fitting the best-fitting model form each class to each half independently, we found that time-variant mechanisms better explained each half of data than time-invariant mechanisms. We further refit the models by removing the early blocks identified as being potentially problematic (see Supplementary Materials), and found a similar result. Taken together, these results suggest that while practice may influence the form of the collapsing decision boundary that each subject adopts in our task, it did not provide support for a fixed boundary policy. As such, we can conclude that practice cannot viably explain why subjects adopt a time-variant strategy to complete our task.

Alternatively, even though practice effects clearly exist in our data, the presence of these effects implies that subjects were not overly practiced on the task. As one of the arguments for the particular shapes of response time distributions was that the non-human primates were overly practiced, the fact that our subjects were not implies that the evidence we found for collapsing bound models is not explainable through only the result of practice.

Stimuli differences

Another potential explanation for the adaption of a collapsing boundary focuses on the properties of the stimuli used in decision-making tasks. Voskuilen et al., (2016) point out that many of the studies that conclude time-variant models provide a better explanation of decision-making behavior have analyzed data from expanded judgment tasks (e.g., Busemeyer & Rapoport, 1988; Drugowitsch et al., 2012; van Maanen et al., 2016), where the rate of evidence accumulation across time is controlled by the properties of the stimuli. The idea is that as the rate of evidence accumulation decreases and the average decision time increases, subjects are more willing to base their decisions on less evidence at later times (i.e., they feel a sense of urgency to respond). Thus, one tenable argument against evidence for collapsing boundaries is that the properties of the stimuli used in these expanded judgment tasks induce a bias toward a time-variant policy, severely limiting this mechanism’s generalizability.

By and large, previous literature does support the notion that the properties of a stimulus can affect a subject’s decision threshold. Namely, time-invariant models appear to better explain data from speeded judgment tasks, which use simple stimuli to induce a fast perceptual judgment, while time-variant models appear to be more suitable for tasks using dynamic stimuli that manipulate the rate of evidence accumulation and the average decision time (e.g., expanded judgment tasks). While, at present, it is unclear whether this division in the literature is due to actual differences in strategy or if it can be explained by the novelty of time-variant models and their lack of application to speeded judgment data, there is currently little evidence to suggest that a boundary collapse is necessary for speeded judgments. However, given we find evidence that subjects collapse their decision boundaries in our task, which featured stimuli more closely aligned with traditional speeded judgment tasks, it seems unlikely that the boundary policy adopted by our subjects can be explained solely by the properties of the stimuli we used.

Task differences

Hawkins et al., (2015) argued that the mechanisms underlying decision-making behavior may vary as a function of task constraint. In their study, they found that two main task characteristics—the administration of reward and the level of practice—served as strong predictors for which model (time-variant versus time-invariant) best described a subject’s data. Regarding reward, in tasks where subjects are required to withhold their response for a certain amount of time, researchers find that it is optimal to adapt a collapsing decision threshold to maximize reward (e.g., Busemeyer & Rapoport, 1988; Ditterich, 2006a; Drugowitsch et al., 2012; Malhotra et al., 2017; Thura et al., 2012). Regarding practice, subjects who complete extensive training sessions prior to commencing a task are often better characterized by time-variant models, while subjects with fewer or no practice sessions are better characterized by time-invariant models, suggesting that collapsing thresholds may result from high levels of practice (Balci et al., 2011; Hawkins et al., 2015; Starns and Ratcliff, 2010).

While these two task constraints served as a viable explanation for the results of Hawkins et al., (2015), they are not applicable to the current study. As subjects received a flat reward at the end of the task that was not contingent on performance and only completed one short practice block, neither reward nor extensive practice can explain the evidence of the collapsing boundary in our results. Additionally, our analyses in Section 2 suggest that practice has little influence on subjects adopting a collapsing decision boundary, further supporting this notion.

However, we do believe that the task demands have induced the need for a collapsing boundary policy in our task. Namely, the coupling of the interrogation and free response paradigms may have induced subjects to attend to the evidence at earlier time points more than at later ones, because on some trials, the stimulus was very brief. It seems plausible that the manipulation of stimulus duration induced a cost on integration time, as integrating for longer periods of time was associated with the risk of the stimulus being taken away. Furthermore, the particular sequence of coherencies we investigated here may have also contributed to the time-variant decision policy according to the optimality analyses presented in Malhotra et al., (2017). In short, subjects learn that some trials are difficult and some are easy. Hence, it seems reasonable to engage in different approaches to solving these different types of problems. On easy trials, because it is easier to engage in the integration process, subjects may use a time-invariant boundary. However, on hard trials, once the subject realizes that the motion signal is very weak, the policy might change toward collapsing their boundary so that they can move on to the next trial in order to reduce the overall amount of energy expended. Such a behavioral dynamic has already been observed in the context of multi-alternative choice (Hawkins et al., 2012), and so we feel that this is the best explanation for why subjects adapt a collapsing decision boundary in our mixed response signal task.

Conclusions

This article contributes to the growing body of literature on the nature of decision processes with respect to time. The purpose of this article was to test whether manipulating the coherency of motion in a speeded judgment task and the duration of stimulus exposure could induce a time-varying decision policy. We found strong evidence supporting time-variant models for all 14 of our subjects, leading us to conclude that this particular experimental manipulation was successful in inducing a time-varying decision policy. As we have discussed, explanations such as the type of stimulus, degree of practice, and reward rate maximization do not seem to be applicable here. Instead, we suspect that the coupling of interrogation and free response paradigms is the most likely explanation of the evidence we have found for a time-varying decision policy.