Perhaps the most common cognitive psychology experiment is one in which participants are presented with stimuli that vary in a dimension of theoretical interest (e.g., stimuli repetition, word frequency, etc.). The stimulus elicits a response, and researchers measure response times (RTs) to draw inferences about hypothesized latent cognitive processes. This form of mental chronometry is commonly used in the analyses of data from a broad range of experimental paradigms such as choice tasks, naming, eye-tracking, and many others.

A critical intellectual endeavor is justifying the logic of the experimental inference—why specific data patterns inform conclusions about latent processes. The most popular model of analysis is tests of mean RTs, which are justified for fairly coarse conclusions. To draw a more fine-grained inference, however, researchers often consider the distributional properties of RTs (Balota & Yap, 2011; Heathcote et al., 1991; Ratcliff, 1979; Rouder et al., 2005). While more fine-grained conclusions are possible, inference based on distributional models often relies on secondary parametric assumptions (Luce, 1986) or commitments to specific processing models such as the diffusion model for choice response times (Ratcliff, 1978) or the EZ-reader model for eye fixation durations during reading (Reichle et al., 1998).

Recently, Sheridan and colleagues (Reingold, Reichle, Glaholt, & Sheridan, 2012; Reingold & Sheridan, 2014, 2018; Sheridan, 2013; Sheridan et al., 2013) proposed a novel mental chronometry method, termed divergence point analysis (DPA from now on), which is claimed to provide finer-grained descriptions of distributional effects without strong assumptions about functional form or a processing mechanism.

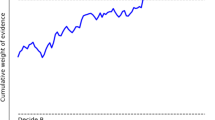
The setup for divergence point analysis applies to the comparison of two experimental conditions (e.g., low predictability vs. high predictability words). The dependent measure is a latency, and this latency can be for a manual response, an event-related component, or an eye-fixation duration. Divergence point analysis is applied to the distributions of latencies across the two conditions. In the broadest definition, the point of divergence is the smallest response time value where the two distributions differ. Figure 1 provides an example in which the cumulative distribution functions (CDFs) are the same below the accentuated point but diverge after it.Footnote 1

Fig. 1
figure 1

Example of a divergence point. Cumulative distribution functions (CDFs) of observed latencies for two conditions that are identical until the marked point. Thereafter, two functions diverge. This representation is typical of plots from Reingold and Sheridan (e.g., Figure 2 of Reingold & Sheridan, 2018)

Full size image

Reingold et al., (2012) offered the following interpretation (in the context of their experiments on the effects of word frequency on eye fixation durations): “[The divergence point] might provide a promising and unique estimate for the earliest significant influence of word frequency on first fixation durations” (p. 185). By extension, the divergence point is the earliest point at which any manipulation first influences a response-time measure.

As we show below, our examination of divergence point analyses lead us to conclude that they are difficult to use for inference about cognitive processes. There are two main problems in the DPA: (1) it has poor construct validity because in most cases the divergence point is trivial; and (2) it has poor statistical properties, as most empirically obtained divergence points are spurious.

Construct validity of divergence points

Reingold et al., (2012) refer to the divergence point as an estimate of first influence. Underlying all estimates is a concept of a true quantity. For example, when we compute the sample mean of a set of observations, we are estimating a true mean for the distribution underlying the sampling of these observations. Likewise, sample variances, sample percentiles, and sample effect sizes all have a true value in the underlying sampling process. Estimates serve as surrogates or best guesses at these true values, and these true values are the target of inference.

In some applications, however, it is difficult to know if the estimate corresponds to anything meaningful. Consider the concept of intelligence. It is always possible to administer tests and tally the scores. The act of tallying the scores, however, does not guarantee that the test measures intelligence or even that a true concept of intelligence exists (Gould, 1996). Whether a test measures its intended target is its construct validity, and construct validity stands as a critical part of measurement.

In the case of divergence point analyses, we believe that criteria for construct validity are in order. In our review of the method, we identified a basic criterion: There must be one true divergence point that the method estimates. Such a divergence point should be non-trivial, which means that it gives us information about the manipulation at hand. Figure 1 shows an example with good construct validity in that there is an actual divergence point that is not trivial. However, as will be shown below, such cases are rare, and not compatible with current information-processing theories.

Trivial divergence points

The lack of construct validity is understood by considering the lower bound of support of a distribution. This lower bound refers to the point below which latencies are not possible; for example, if latencies follow an exponential distribution that admits only positive response times, the lower bound is zero. Lower bounds need not be finite; for example, the lower bound for the normal and ex-Gaussian distributions are −∞. In most process models, the lower bound is a free parameter, called the irreducible minimum, which denotes a minimum time for encoding the stimulus and making a motor response (Dzhafarov, 1992; Luce, 1986; Ratcliff, 1979). Examples of such models include the diffusion model (Ratcliff, 1978) where the lower bound is Ter, race models (Rouder et al., 2005) where the lower bound is ψ, and the linear ballistic accumulator (Brown and Heathcote, 2008) where the lower bound is T0.

We call a divergence point trivial if (a) both distributions share the same lower bound of support, and (b) the divergence point is at this lower bound of support. Consider the divergence point of two ex-Gaussian distributions that only differ in τ (i.e., the tail parameter) while the values of μ and σ are identical in both conditions. One might expect a divergence point in this setup, as the underlying factor seemingly affects a late component in the distribution. Figure 2a and b show the density functions and the CDFs, respectively, for this setup. Perhaps counter-intuitively, the CDFs have no common points to diverge from. Instead, the distribution with the smaller exponential scale is faster everywhere. If one is to talk about a divergence point at all, it would be at −∞, which in this case is the lower bound of support.

Fig. 2
figure 2

Density functions and cumulative distribution functions for ex-Gaussian distributions that have trivial divergence points. For both distributions mu = 300 and sigma = 100, tau is 150 for the distribution is represented with black lines, and tau = 300 for the distribution represented with a light line

Full size image

As it turns out, trivial divergence points are the norm in experimental situations. For example, this triviality holds in situations in which the μ parameter is affected in the same direction as the τ parameter by an experimental manipulation. This situation is quite ubiquitous, particularly for first-order effects like word frequency (see for example Table 1 in Staub, 2011, in which the frequency effects in first fixation duration are Δμ = 16ms, and Δτ = 10ms).

Trivial divergence points are common in distributions with finite lower bounds of support. Take, for example, the diffusion model. Trivial divergence points occur when any parameter is affected, except for the Ter, the lower bound. The usual experiment is designed to affect drift rate, bound, or starting points, and these usual cases imply a trivial divergence.

Figure 3 shows some processes that result in trivial divergence. Each of the panels represents a process model with different assumptions regarding the source of variability in the latency distribution. In Fig. 3a, the first mechanism is the same for the two conditions, it has a mean of 382 ms, and a standard deviation of 50 (analogous to the T0 & ST parameters in diffusion models). The beginning of the second process (the linear activation function) occurs at the end of the first process, and the latency is the point in time at which the activation reaches the threshold. Even if we assume that there is no variability in the activation rate within a category, the true divergence point is the shift value, which is trivial.

Fig. 3
figure 3

Four scenarios for plausible mechanisms of decision-making under a simplified linear activation function. For each of the panels, the bottom part represents the activation processes, the middle part represent the density function for the latencies, and the top panel represents the cumulative density functions. In the four panels, the distributions that have trivial divergence points. See the main text for an explanation of each of the mechanisms

Full size image

In the scenario represented by Fig. 3b, we changed the locus of variability. In this case, the ending of the first process is constant at 382 ms, while the rate of activation of the second process varies within each condition. Again, the divergence point is trivial and corresponds to a cumulative probability value of zero. For Fig. 3c, we included variability in the ending time of the first process and variability in the activation level of the second process; again, while the two conditions are identical for the first component, and vary only on the second component, the divergence point is trivial and corresponds to a cumulative probability value of zero.

Figure 3d represents the assumption of activation beginning at time zero, and the second process affecting such activation only after the divergence point. We assume some variability in the first process, but no difference between conditions, and a difference between conditions for the second process but without variability. In other words, the variability in this mechanism is restricted to the beginning activation. Again, the divergence point is trivial. Any combination of variability like the ones explored in Fig. 3a–d will generate a trivial divergence point. These examples raise the question of whether any process models yield a true non-trivial divergence points like that in Fig. 1.

Valid divergence points

The above cases show that typically there will only be trivial divergence point to analyze—that is, there is no construct validity to the estimate; however, we challenged ourselves to come up with a model where there was a true divergence point that was not trivial. We were able to generate cases such as those in Fig. 4a and b. Figure 4a is constructed as a horse race: Let the response latency be the fastest of two processes (represented by the dashed and the solid lines). One of the two processes is identically distributed in the two conditions (we will refer to it as the “D” process, as in the D ashed lines in the figure); the other process has, on average, lower activation rates and is represented in the figure by the solid lines (we will refer to is as the “S” process for the S olid lines in the figure). Critically, there is a difference between conditions for the “S” process. The shortest RTs come from the “D” process, and because this process does not vary between conditions, the density and the CDF are identical for the two conditions until a divergence point. This non-trivial divergence point emerges only under very specific parameter combinations and under the assumption of no other sources of variability in the latencies.

Fig. 4
figure 4

Density function and the cumulative distribution function for distributions that have a non-trivial divergence point. See main text for an explanation of each of the mechanisms

Full size image

The second example of non-trivial divergence point is presented in Fig. 4b. In this case, the assumption is that the first process is identical between the two conditions and that the activation threshold can be reached with this process alone. The second process does not come into play until a later point in time (the vertical dashed line) and only if the threshold has not been reached. In this second process, there is a difference between the two conditions. As can be seen, this example does generate a non-trivial divergence point. Unfortunately, we believe that this is an unrealistic scenario. The density functions look unusual (see Fig. 4b). The reason is apparent—the divergence point marks a sudden change in derivative in the CDFs. This derivative of the CDF is the density function, and these sudden changes imply violations of the absolute continuity of the density. The result is awkward distributions.

We can think, however, of some theoretical claims that could be consistent with Fig. 4b. In recognition memory tasks, some researchers have posited that familiarity is somewhat independent of recollection and that familiarity occurs earlier that recollection processes (Rotello & Heit, 1999). One could conceivably construct an experimental manipulation in which there are no familiarity differences between conditions, while there is a recollection advantage for one of the conditions. We suspect that in almost all other applications, the true divergence point will be trivial and that the estimate will lack construct validity. It remains an open challenge for proponents of the DPA to show that non-trivial true divergence points are plausible.

Statistical properties of divergence point analyses

In the previous section, we made a case for more in-depth scrutiny of the construct validity of DPA; in this section, we describe some problematic statistical properties that emerge from the lack of construct validity. First, we analyze the behavior of the DPA under the assumption of a null effect; then, we examine two scenarios that have been reported in the literature and appear to yield non-trivial divergence points.

Spurious divergence points

The lack of construct validity of DPA manifests itself as poor statistical properties that take slightly different forms depending on the specific implementation of the method. It is important to emphasize that we believe that these statistical issues are a consequence of the lack of construct validity in the method.

In Reingold & Sheridan’s (2014) bootstrapping method, in each iteration the latencies for each participant in each condition are randomly re-sampled with replacement. Each participant’s survival curves are then computed, to be averaged across subjects (à la Vincentile). Next, for each time bin t, the differences between conditions: Δti are computed (i stands for the number of iteration of the bootstrapping method), and then sorted. The range between the 5th and the 9995th value becomes the confidence interval CI(Δt) and the divergence point becomes the shortest t at which the CI(Δt) does not include 0. Researchers can decide the size of the bins.

A number of researchers have recently used this method (e.g., Leinenger 2018; Schmidtke & Kuperman 2019; Schmidtke, Matsuki, and Kuperman, 2017); however, Reingold & Sheridan (2014) abandoned this original bootstrapping method to find the first point of divergence. They realized that “…divergence point would be delayed relative to the actual point of divergence. This would be especially the case under low experimental power (i.e., a small number of participants and observations)” (p. 3), hence the bias of the bootstrapping method will not be discussed here.

The new method, termed ex-Gaussian DPA relies on a two-step process. In the first step, latencies are fit with ex-Gaussian distributions, and then the parameters are used to generate CDFs. When the CDFs vary by more than .015, the method detects a divergence point.

What happens if there is no true divergence because the true distributions for the two conditions are identical? We carried out a set of simulations with this scenario in mind. There are many ways to carry out these simulations with many parameters to vary; here, we present best-case scenarios with the following assumptions: (1) for both conditions under comparison, the latencies were sampled from identical ex-Gaussian distributions; (2) although we varied the μ, σ and τ parameters across simulations, within each simulation the values were identical for all participants; and (3) we varied the number of participants and number of items per condition.

Given that the latencies from both conditions come from the same distribution, there is no true divergence point (not even at T0). If the DPA produces a divergence point, we refer to it as a spurious divergence point. We carried out simulations with three levels of μ values (50,100,150), three levels of σ values (30,60,90), three levels of τ values (50,100,150), four levels of number of trials per condition (20, 40, 80, 160), and four levels of number of participants (20, 40, 80, 160), for a total of 432 simulations (3 × 3 × 3 × 4 × 4 = 432), for each combination of parameters, there were 500 simulated experiments. The RTs were generated with the rexGAUS function of the gamlss.dist package, and the ex-Gaussian fits were done with the timefit function of the of the retimes package in R.

Figure 5 shows the rate of spurious divergence points for different numbers of trials and participants and for the three levels of μ and τ (in the figure we present only the simulations with σ = 60ms; other values of σ do not lead to different conclusions, but the complete set of simulations is available in the online appendix). In Table 1, we present an illustrative subset of the simulations (μ = 100, σ = 60 and τ = 50), the rate of spurious divergence points can be quite large, particularly for the number of trials and participants that are common and feasible in cognitive psychology experiments and psycholinguistics studies, in which there might be a limited number of possible materials to study the phenomenon of interest.

Fig. 5
figure 5

Different panels display the proportion of found divergence points assuming that there is no difference between the two conditions under comparison. The columns of panels represent the values of the mu parameter, and the rows represent the value of the tau parameter; sigma = 60 for all simulations. As would be expected, the rate of spurious divergence points is determined by the number of trials per condition (the x-axis within each panel), and the number of participants (the lines within each panel)

Full size image
Table 1 Rate of spurious divergence points for simulations with null effects
Full size table

The reason for such a large rate of spurious divergence points is straightforward: even small deviations in the sample data relative to the population parameters will yield differences in the ex-Gaussian parameters of the fits, and even very small differences in those parameters, for example a difference of a couple of milliseconds, will yield differences of .015 in the CDF/survival function. The ex-Gaussian fits are done on noisy data, and the method picks up the divergence in the noisy data. At large number of trials and participants, the DPA does a very good job of not returning a spurious point; the method does have consistency in that respect: as the number of observation increases, the method is less likely to give researchers an incorrect answer.

Divergence points that are CDF crossings

In recent work, Reingold & Sheridan (2018) have described CDF crossing points in simulation as divergence points. Thinking of these situations in terms of ex-Gaussian parameters is useful. Sheridan and Reingold consider cases with interacting effects where μ and τ are affected in opposite directions. Figure 6 is taken from the table in the Appendix of Sheridan and Reingold, and it shows a series of differences from their simulations. Each point is for a simulation run. Note how positive differences in one parameter are associated with negative differences in the other. The overlaid table shows, as an example, the values for one data point. In this chosen point, the value of the μ parameter of the ex-Gaussian for the “slow” condition is smaller than the value for the “fast” condition. In contrast, the value of the τ parameter is larger in the slow than in the fast condition. Such crossovers seem quite informative, as they indicate that the same manipulation has a facilitative effect in one component of processing, while it was an inhibitory effect in another.

Fig. 6
figure 6

Effects on mu and on tau taken from Reingold and Sheridan (2018) Appendix 1. These were parameters used to find non-trivial divergence points in their simulations. While this would represent an interesting set of parameters in their own right, they are somewhat unusual; this is because across many experiments, the effects on mu and on tau tend to be positively correlated, not negatively correlated, as in the figure. The shade of the points relates to the location of the divergence point according to the DPA method

Full size image

The claim by Reingold and Sheridan is that these scenarios give rise to cases that have nontrivial divergence points, which are accurately localized by their divergence point analytic methods. We have three critiques of this. First, crossover points are not divergence points. They are not the earliest point at which distributions differ. The distributions differ throughout the range, and in this case, the divergence is trivial. Second, crossover points are exceedingly rare in practice. There are a few examples in the literature (Rouder, 2000; Yantis et al., 1991), but the vast majority of studies show no such crossover. Third, crossovers are diagnostic of a mixture of processes (Everitt & Hand, 1981; Falmagne, 1968). In such a scenario, the main theoretical implication is not the time of crossover, but what is the interpretation of the components and how are they affected by the manipulations at hand (See Fig. 7).

Fig. 7
figure 7

We present two examples of divergence points. Panels a and b show crossovers in the survival functions; the fast condition is shown with dashed lines

Full size image

If researchers are looking for ways to describe these types of crossovers and dissociations between components of latency distributions, we believe that delta plots (e.g., De Jong, Liang, & Lauber, 1994; and particularly Ellinghaus & Miller, 2018 for delta plots with negative slopes) provide a far more cohesive and informative view.

Furthermore, the estimates from the DPA method in the crossover situation can be quite volatile. An example is provided by Reingold and Sheridan (2018) in their appendix for a divergence point of 180 ms. Figure 8 shows the survival functions using parameters similar to those in their table: for Condition 1: μ1 = 150, σ1 = 60, τ1 = 78, and for Condition 2; μ=147, σ2 = 64, τ2 = 91.

Fig. 8
figure 8

Illustration of how small changes can yield large fluctuations in the DPA results. The three panels show distributions with small variations in the mu parameter (150 ms to 160 ms to 161 ms) for one of the conditions, which yields widely different divergence points

Full size image

Critically, even minuscule changes in the parameters generate radically different divergence points. For example, if the μ1 parameter goes from 150 ms to 160 ms, to 161 ms, the divergence point goes from 183 ms to 287 ms in favor of Condition 1, to 75 ms in favor of Condition 2.

This finding complements the analysis shown in the previous subsection on spurious divergence points. Small variations due to sampling can produce radically different results, from spurious divergence points, to large swings in the value and direction of the divergence point.

Conclusions

Divergence points have limited interpretation. The apparent lack of true divergence points may seem counter-intuitive. For example, if we consider a reading task where participants decide if presented words are nouns or verbs, then we might expect that forming a representation in visual cortex occurs before the influence of the part-of-speech manipulation. This hypothetical might imply the plausibility of a divergence point. The part of speech manipulation does not affect the time course of processing before semantic meaning evaluation.

This hypothetical, which we find compelling, highlights the difficulty in interpretation. Divergence point analysis is not about moment-to-moment processing (see Estes, 1956 for another example of the difficulty in the interpretation of grouped data). It is possible, even likely, that there are manipulations that do not affect the moment-to-moment processing up to a specific point in time, after which there is a divergence in processing, yet, there are no divergence points in the collection of response time distributions. Divergence point analysis is about the response time distributions, and such a point cannot be interpreted in terms of latent moment-to-moment processing. Reingold and Sheridan (2018) acknowledge this issue; but this limitation is severe, and it constrains the usefulness and attractiveness of the method greatly. For the utmost transparency, users of the method should be explicit about these issues.

In most situations, the divergence point will be trivial, as in most experimental manipulations there is stochastic dominance: meaning that across all quantiles, the CDF for a fast condition will be to the left of the CDF for the slow condition regardless of what component (early vs. late) of processing is being tapped into. In the minority of experimental manipulations, there can be a dissociation between early components and late components; this can be easily implemented in process models like the EZ reader or evidence accumulation models. In these cases, the CDF might cross, and that crossing might be picked up by the DPA. We believe that if researchers want a purely descriptive, exploratory data analysis (EDA, Tukey, 1967) method, delta plots are better suited than DPA. Also, researchers could use linear mixed effects to explore the slope and intercept of the delta plots if inferential methods are in order (this, of course, deserves further examination).

In yet a smaller proportion of cases, there might be a true non-trivial divergence point. These situations are rare, and we had to think hard to come up with architectures that yield this type of effects. If the researcher’s model of the task is indeed one that generates a non-trivial divergence point, we believe that a DPA method might provide useful information. Note, however, that such architectures do not generate ex-Gaussian distributions, and hence fitting such functional form to the data might, or might not recover the true, non-trivial divergence point (we present examples in the online appendix). Nevertheless, we remain skeptical that such cases exist.

In sum, the divergence point analysis methods suffer from poor construct validity, and hence, also of poor statistical properties. For these reasons, its usefulness is limited, and researchers should pause before using it.

Open practices statement

The code used to generate the figures and the simulations is available at https://osf.io/ghw37/ R (Version 3.6.1, R Core Team, 2019).Footnote 2