Testing, or retrieval practice, has been shown to improve retention of memory relative to a nontest control task across a variety of materials and test types (a phenomenon known as test-enhanced learning, or the testing effect; for reviews, see Roediger & Butler, 2011; Rowland, 2014). The testing effect is particularly potent if correct answer feedback occurs immediately after each trial (Kang, McDermott, & Roediger, 2007).

For cued-recall testing, which is the focus of the current paper, one common experimental design involves (a) a study phase, in which all items are passively studied; (b) a training phase, in which the experimental manipulation occurs—half of the items are presented for restudy (the restudy condition) and half undergo a cued-recall test with feedback (the test condition); and (c) a delayed final-test phase, in which all items are tested. In their review of the literature in which that experimental design has been used, Rickard and Pan (2018) found a positive testing effect on the final test (i.e., higher proportion correct in the test condition than in the restudy condition) for 96% of 114 experiments. Along with other approaches, such as spaced and interleaved practice, testing is widely regarded as one of the more promising cognitive approaches to improving learning in educational contexts.

The mechanisms by which testing enhances later performance are currently under investigation. Among the influential accounts in the recent literature are the bifurcation theory (Kornell, Bjork, & Garcia, 2011), the elaborative retrieval theory (Carpenter, 2009), the mediator effectiveness hypothesis (Pyc & Rawson, 2010), and the episodic context theory (Karpicke, Lehman, & Aue, 2014). Each of those theories (among others) advances a viable candidate mechanism, with varying degrees of empirical support.

The dual-memory theory

A limitation in the current literature, however, is a scarcity of quantitatively based models that can be fitted to data across a set of core testing-effect phenomena. An exception is the dual-memory model proposed by Rickard and Pan (2018), which is a special case of their dual-memory theoretical framework for test-enhanced learning. The theoretical framework states that the study phase yields a study memory for each item. Restudy in the training phase strengthens that study memory without creating a separate memory. In contrast, a training-phase cued-recall trial with immediate correct answer feedback (henceforth, feedback) both strengthens study memory and encodes a separate test memory of the combination of the retrieval cue and the correct response, regardless of whether the correct answer is retrieved. Study-memory strengthening occurs on a test trial with feedback because either (a) on correct test trials, study memory is accessed to retrieve the correct answer, or (b) on incorrect test trials, study memory may be accessible and strengthened after feedback is provided. Although recent evidence suggests that there are distinct properties of study memory and test memory (e.g., Rickard & Pan, 2020), for current purposes, those differences are not critical.

The testing effect is observed because there are two routes to retrieval for items in the test condition (through study memory and test memory), but only one route to retrieval for items in the restudy condition (through study memory), and because study memory can be strengthened on both restudy and test trials. Provided that retrieval success through study memory and test memory for tested items is not highly correlated, final-test performance is expected to be better in the test condition than in the restudy condition.

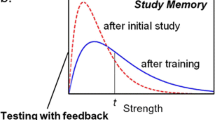
Given additional, simplest case assumptions that are psychologically viable and, in some cases, have independent empirical support, a quantitative model was derived from that theory. The reader is referred to Rickard and Pan (2018) for a detailed treatment of that model. One core property of the model is that, on the final test, the memory strength distributions over items are equivalent for (1) study memory in the restudy condition, (2) study memory in the test condition, and (3) test memory in the test condition (the identical distributions assumption; see Fig. 1). For a randomly selected item in either the restudy or test condition, correct retrieval through any one of those memory distributions will occur only if memory strength is above a fixed threshold value. Probability correct is thus the portion of the strength distribution that is above the threshold. Further, study-memory and test-memory strength distributions over items are assumed to be independent. Following the product rule for independent events, probability correct in the test condition is predicted to be a quadratic function of probability correct through study memory and probability correct through test memory. Because of the identical distributions assumption, that probability can be expressed solely as a function of probability correct in the restudy condition (see Fig. 1). Hence, for an idealized subject with an infinite number of items, the predicted probability correct in the test condition (PT) is,

$$ {P}_T=2{P}_R-{P}_R^2, $$
(1)

where PR is the probability correct in the restudy condition. The predicted magnitude of the testing effect (TE) is,

$$ TE={P}_T-{P}_R={P}_R-{P}_R^2 $$
(2)
Fig. 1
figure 1

Depiction of the memory strength distributions on the final test and the corresponding quantitative predictions of the dual-memory model. SR = study memory strength for a randomly selected item in the restudy condition; ST-s = study memory strength for a randomly selected item in in the test condition; ST-t = test memory strength for a randomly selected item in in the test condition; PT-s = probability correct through study memory for a randomly selected item in in the test condition; PT-t = probability correct through test memory for a randomly selected item in in the test condition

Full size image

For an experimental subject, the same quadratic equations describe the expected proportion correct in the test condition, E(PCT), and the expected TE, E(TE),

$$ E\left({PC}_T\right)=2{PC}_R-{PC}_R^2, $$
(3)
$$ E(TE)={PC}_R-{PC}_R^2, $$
(4)

where PCR is the observed proportion correct in the restudy condition.Footnote 1

For example, if for a given subject the observed proportion correct in the restudy condition on the final test is .3, then the expected test-condition proportion correct is 2 × .3 − .32 = .51, and the expected TE is .3 − .32 = .21.

That quantitative model has three properties that support predictions about the mean test condition proportion correct and the mean testing-effect magnitude, and also about proportion correct distributions and individual differences that are the focus of this paper: (1) it has no free parameters, (2) predictions are independent for each subject, and (3) predictions are interval scale.

Although it is unlikely that any parameter-free model will hold for testing-effect studies in the general case, for an experimental design that distills the testing effect with minimal extraneous factors, the dual-memory model has provided viable empirical accounts at the level of condition means of several core phenomena (see Rickard & Pan, 2018). These include but are not limited to (1) the mean proportion correct in the test condition and the mean testing-effect magnitude, (2) the effect of training-test feedback (present or absent), and (3) the retention function for the cases of both feedback and no feedback.

Testing the dual-memory model at the distribution level

It is well known that analyses at the distribution level can reveal differences between experimental conditions, or between a model and data, even when a comparison between means cannot (e.g., Balota & Yap, 2011). In the current paper, two proportion correct distributions over subjects were compared: (1) the observed proportion correct distribution for the test condition, and (2) the expected proportion correct distribution for the test condition, based on Equation 3. If the model’s expected value prediction is correct for each subject, then in the hypothetical subject population, the distributions of observed and predicted test-condition proportions correct will be identical, and in a sample, they will be stochastically equivalent. That distribution prediction has not been previously tested. Indeed, there appear to be no distribution analyses of the testing effect in the current literature.

Individual differences

The dual-memory model takes a unique stand on how individual difference (ID) factors (such as episodic memory ability, working memory ability, and intelligence) influence test-condition performance and testing-effect magnitude. Specifically, the model predicts that all task-relevant IDs will equivalently moderate the study and test memory strength distributions (with no other effects), preserving the identical distributions assumption and hence the equation predictions for each subject. If the model equations successfully predict the distribution of test-condition proportion correct over subjects, then its account of aggregate ID effects is supported.

Data sets

The model was tested on proportion correct data from multiple data sets that were collected in our laboratory (see Table 1), in which the same core experimental design was used (a design closely related to that of Carpenter, Pashler, & Vul, 2006). That design distills the events and manipulations that are necessary to explore the testing effect and is thus well suited for developing and testing a quantitative model. Each experiment entailed the following:

  1. 1.

    Three experimental phases over two sessions: the study and training phases in Session 1 and the final-test phase in Session 2.

  2. 2.

    Presentation of each item once, for either 6 or 8 s each, depending on the experiment, during the study phase. Following the literature, no response was required on study trials (nor on restudy trials in the training phase).

  3. 3.

    A within-subjects manipulation during the training phase involving (1) random assignment of items into two subsets with counterbalanced assignment of those subsets to the restudy and testing conditions, (2) randomly intermixed restudy and test with feedback trials, (3) a single presentation of each item, (4) equated exposure time (6 or 8 s) for restudy and test with feedback trials, and (5) on test trials, instructions to type the response quickly and accurately. In all experiments, the elements (familiar words) constituting the items (word pairs, triplets, or history facts) had weak associative strength, necessitated retrieval of the correct response from the episodic memory that was formed during the study phase. In both the training and final-test phases, the same single word always constituted the correct response.

  4. 4.

    On the final test (which, for current purposes, included only the first block of trials from each experiment), there was one cued-recall trial for each restudied and tested item, randomly ordered, using the same cued-recall format as on the training test. There was no trial time limit, and no feedback was provided.

Table 1 Studies from our laboratory included in the primary distribution analyses
Full size table

All data sets collected in our laboratory that match the experimental properties noted above were included in the current analyses. The data sets varied with respect to type of material (word pairs, word triplets, and history facts) and retention interval (1, 2, or 7 days). Data Sets 3 through 10 involved a third final-test condition (in addition to the test and restudy conditions) that assessed transfer of test enhanced learning. Model fit quality did not depend on whether that third condition was present, and data from that condition were not analyzed here. On the final, test there were 20 items in the test condition in Data Sets 1 and 2, and nine (or in one case, six) items in the test condition in the remaining data sets. Across all data sets, there were either 18 or 20 items in the restudy condition.

Results and discussion

The dual-memory model is tested here using empirical cumulative distribution analyses. The cumulative proportion correct for the test condition was compared with the predicted cumulative proportion correct for the test condition (Equation 3). Each cumulative distribution was found by sorting the proportions correct over subjects from smallest to largest and plotting those proportions by quantile, which was scaled to have values between zero and one (e.g., for the plots involving the full set of 509 subjects, there were 509 quantile values, all equally spaced from about .002 to 1). That sorting was performed independently for the observed test-condition proportions correct, the predicted test-condition proportions correct, and, for reference, the observed restudy-condition proportions correct.

Results for the full set of 509 subjects are shown in Fig. 2. By visual inspection, the model fit is very good, particularly given the absence of free parameters. That impression is consistent with results of a two-sided Kolmogorov–Smirnov (K-S) test for two samples (i.e., observed and predicted test-condition proportion correct): D = .0559, p = .204. Note that this distribution fit does not imply that all of the subjects exhibited a positive testing effect. In fact, a negative effect was observed for 16% of subjects. However, the good fit of the model suggests that the testing-effect true score (Equation 2) was positive for at least the great majority of subjects.

Fig. 2
figure 2

Final-test cumulative distribution results for the full data set

Full size image

The experiments that constitute the full data set varied over both material type and retention interval (see Table 1), and based on Rickard and Pan (2018), both of those sources of variation should be accommodated by the model. Distribution results limited to the paired associate data (n = 333) are shown in Fig. 3a (K-S test: D = .0559, p = .35), and results limited to the triplet and fact data (n = 176) are shown in Fig. 3b (D = .1235, p = .07). Results limited to the data with a 1-day or 2-day retention interval (n = 413) are shown in Fig. 4a (D = .0559, p = .275), and results for data with 7-day retention intervals (n = 96) are shown in Fig. 4b (K-S test: D = .151, p = .11). The model holds to good first approximation in each of those cases, although for the 7-day retention interval there is a hint that the model underestimates the TE, raising the possibility that it will not fit data as well at longer intervals.

Fig. 3
figure 3

Final-test cumulative distribution results for subjects in the paired associate experiments (a) and for subjects in the triplet and fact experiments (b)

Full size image
Fig. 4
figure 4

Final-test cumulative distribution results for subjects in the 1-day and 2-day retention experiments (a) and for subjects in 7-day retention experiments (b)

Full size image

One instructive pattern in Figs. 2, 3, and 4 is that proportions correct in the test and restudy conditions converge on zero at roughly the same lower tail quantile. Although that pattern is predicted by the model, it does not appear to be predicted by other modeling frameworks. Consider any theory that assumes that the initially encoded study memory is modified more effectively by a training phase test with feedback than by a training phase restudy trial, and that also assumes that a single integrated memory exists after training for both restudied and tested items. If implemented quantitatively, that class of models would appear to predict that cumulative test-condition proportions correct will remain above zero, perhaps substantially so, as cumulative-restudy condition proportion correct approaches and reaches zero.

The distribution results are also consistent with the model assumption that learning on test with feedback trials is not causally dependent on response accuracy (Rickard & Pan, 2018; see also Kornell, Klein, & Rawson, 2015). To more incisively investigate that issue, residual difference scores (predicted minus observed test-condition proportion correct at each quantile in Fig. 2) were plotted against training-test proportion correct, wherein each subject’s training-test proportion correct was matched to the residual difference score that contained that subject’s observed test-condition proportion correct. According to the dual-memory model and the conclusions of Kornell et al. (2015), there should be no trend toward the residual scores becoming either more positive or more negative as training-test proportion correct increases. The results, shown in Fig. 5, are in agreement with the model.

Fig. 5
figure 5

Final-test residual difference scores (predicted minus tested) plotted as a function of matched training-test proportion correct

Full size image

Implications for individual differences in the testing effect

The distribution results are consistent with the claim of the model that ID factors influence TE magnitude by equivalently influencing the retrieval probability from study and test memory. In drawing that conclusion, it is assumed that a substantial portion of the observed performance variability over subjects reflects ID factors, rather than random variation about a single population probability correct. That assumption was tested against the null hypothesis of no ID effects using the binomial distribution. If there are no ID effects in the data, then the expected distribution of number of items correct (number correct) in the final-test restudy condition can be reasonably modeled by generating a number correct for each of 509 simulated subjects (i.e., 509 random deviates from the binomial distribution) in which the probability correct for each final-test trial, p, is the same for each subject and item (specifically in this case, .34, the grand mean proportion correct in the restudy condition). The number of trials for each simulated subject, n, corresponded to the number of trials in the restudy condition for each of the experimental subjects (18 or 20 over experiments). Proportion correct for each simulated subject was then calculated by dividing the simulated number correct by n.

Results are overlaid on the observed restudy cumulative proportion correct in Fig. 6. The actual variability in the restudy condition greatly exceeds that predicted by the null binomial model. An analogous pattern would hold if the simulation were applied to the test condition. Not surprisingly, then, IDs appear to play a major role in the performance differences over subjects in the current data.

Fig. 6
figure 6

Final-test cumulative distribution results for the restudy condition of the full set, overlaid on the predicted restudy distribution for the hypothetical case of no individual differences

Full size image

The dual-memory model does not imply that subjects with relatively low or high ability on ID factors will always have smaller TEs than those with intermediate ability, as one might infer through casual inspection of Fig. 2. Rather, the model predicts that restudy proportion correct for a given subject is determined by an interaction between task-relevant IDs and inherent task difficulty (a reasonable assumption for any applicable model), and that restudy proportion correct has a quadratic effect on testing-effect magnitude. Experimental evidence is generally consistent with that interaction claim: Minear, Coane, Boland, Cooney, and Albat (2018) observed a crossover interaction between item difficulty and intelligence, such that the testing effect was largest for two of the four combinations: higher intelligence–difficult items and lower intelligence–easy items.

The theoretical approach to individual differences taken in this paper is distinct from the more exploratory approach take in the broader testing-effect literature, in which analysis of correlations between particular ID variables and the testing-effect magnitude predominate (for review, see Unsworth, 2019). The dual-memory model does not make direct predictions about such correlations. Rather, it allows for either positive or negative correlations in any given experiment. That fact is a consequence of the nonlinear (quadratic) relation in the model between restudy proportion correct and the TE (Equation 4; see also Fig. 5 of Rickard & Pan, 2018). In the model, any correlation between an ID variable and the TE is (in part) a joint consequence of (1) the relation between the ID variable and restudy proportion correct, and (2) the relation between restudy proportion correct and the TE. For example, one would expect a positive correlation between a subject’s score on an episodic memory (EM) assessment and their restudy proportion correct, particularly because tasks used in EM assessments typically include study followed by cued recall. If, in addition, all subjects in the sample have restudy proportions correct that are less than .5, then a positive correlation between restudy and the TE is expected (i.e., the quadratic function relating restudy performance to the TE is monotonically increasing up to PCR = .5). By transitive inference, the model implies a positive correlation between the EM scores and the TE in that case, although the magnitude of that correlation will be determined by the sampling variability of those proportion correct values. In contrast, if all subjects in that experiment have restudy proportions correct that are greater than .5 (e.g., by simply shortening the retention interval substantially to improve overall final-test performance), then by the same reasoning a negative correlation between that the EM assessment and the TE would be expected. Finally, if restudy proportions correct are evenly distributed below and above PCR = .5, then a correlation that is close to zero would be expected.

Limitations and future directions

The dual-memory model was developed in the context of a simple, well-controlled experimental design. The fact that its distribution and ID predictions hold in that context lends credence to its theoretical process claims. An important goal for future work will be to evaluate the model against cued-recall testing-effect experiments that were conducted in other laboratories with varying experimental designs. It remains to be seen whether the model will fit well across such changes. In fact, for two large cued-recall data sets (Brewer & Unsworth, 2012; Robey, 2017), the mean TEs were smaller than for the current data sets, raising the possibility of poorer model fits. Broadly, however, we anticipate that the model will generalize well over laboratories, subject populations, and materials. We anticipate that the model may not generalize well to designs involving multiple training phase item repetitions or to contexts in which subjects are prompted to use especially effective learning strategies during restudy (for further discussion, see Rickard & Pan, 2018). Such cross-study comparisons should increase our general understanding of the testing effect for cued recall, may establish boundary conditions for applicability of the dual-memory model, or may provide insight into an alternative and more complete quantitative model of the phenomena.