Systematic angular biases in the representation of visual space

Abstract

Representing spatial information is one of our most foundational abilities. Yet in the present work we find that even the simplest possible spatial tasks reveal surprising, systematic misrepresentations of space—such as biases wherein objects are perceived and remembered as being nearer to the centers of their surrounding quadrants. We employed both a placement task (in which observers see two differently sized shapes, one of which has a dot in it, and then must place a second dot in the other shape so that their relative locations are equated) and a matching task (in which observers see two dots, each inside a separate shape, and must simply report whether their relative locations are matched). Some of the resulting biases were shape specific. For example, when dots appeared in a triangle during the placement task, the dots placed by observers were biased away from certain parts of the symmetry axes. But other systematic biases were not shape specific, and seemed instead to reflect differences in the grain of resolution for different regions of space. For example, with both a circle and even a shapeless configuration (with only a central landmark) in the matching task, observers were better at discriminating angular differences (when a dot changed positions around the circle, as opposed to inward/outward changes) in cardinal versus oblique sectors. These data reveal a powerful angular spatial bias, and highlight how the resolution of spatial representation differs for different regions and dimensions of space itself.

The ability to accurately perceive and represent space is vital to our success as a species. This is intuitively obvious in the context of skills such as navigation—because even getting to and from your home each day would be impossible without spatial representations. But, in addition, spatial representations are also thought to lie at the foundation of many other cognitive processes, from object representation (e.g., Driver, Davis, Russell, Turatto, & Freeman, 2001; Kahneman, Treisman, & Gibbs, 1992), to numerical processing (e.g., Dehaene, Bossini, & Giraux, 1993; Zorzi, Priftis, & Umiltà, 2002), to reasoning about social relationships (e.g., Parkinson & Wheatley, 2013).

Spatial representation and spatial biases

Ever since classic work on the ‘cognitive map’ (Tolman, 1948), a great deal of research has been devoted to explaining the nature of spatial representations. Some of this work appeals to an underlying coordinate system, in which objects can be represented in absolute terms—as in proposals for a Euclidean map that represents locations and spatial relationships in a common coordinate system (e.g., Gallistel, 1990; O’Keefe & Nadel, 1978). (Such representations are often thought to be supported by ‘place cells’ that fire selectively to specific locations; e.g., O’Keefe & Dostrovsky, 1971.) Other work appeals to more relative sorts of representations, in which locations are represented via their angle and distance relationships to other objects (e.g., Kuipers, Tecuci, & Stankiewicz, 2003; Werner, Krieg-Brückner, & Herrmann, 2000), and some animals navigate via representations of egocentric paths, based, for example, on counting the number of steps taken (e.g., McNaughton, Battaglia, Jensen, Moser, & Moser, 2006; Müller & Wehner, 1988). (And these sorts of representations are sometimes thought to be supported by ‘grid cells’ that fire selectively to periodic regions of space with a particular hexagonal structure; e.g., Moser, Kropff, & Moser, 2008; Moser et al., 2014.) And still other work (demonstrating success in the face of massive Euclidean inconsistencies in virtual environments, due to ‘wormholes’) suggests that space is instead represented in a graph-like network format (e.g., Warren, Rothman, Schnapp, & Ericson, 2017).

Despite its importance, spatial processing is notoriously inexact. Indeed, entire volumes have been devoted to understanding various types of spatial errors (e.g., Hubbard, 2018). Many of these errors relate to specific actions, such as pointing or navigation, that are beyond the scope of the present project, but some of them seem to implicate the nature of spatial representation itself. In particular, there are two classes of biases that will be especially relevant to the current experiments, both of which we return to in the General Discussion. First, there are what have sometimes been referred to as ‘prototype’ effects—striking biases of spatial memory in which objects are remembered as having been closer to centers of the quadrants in which they originated (e.g., Huttenlocher, Hedges, & Duncan, 1991; Huttenlocher, Hedges, & Veva, 2000; Langlois, Jacoby, Suchow, & Griffiths, 2017; McNamara, 1986; Wedell, Fitting, & Allen, 2007). Second, there is the ‘oblique effect’—the phenomenon in which observers are worse at processing information along tilted lines compared with horizontal or vertical lines (e.g., Appelle, 1972; Furmanski & Engel, 2000; Keil & Cristóbal, 2000).

The current study

The current project asks how foundational spatial biases may be, in two ways. First, we ask whether they appear even in the simplest possible spatial tasks. In contrast, for example, past work on the ‘prototype effect’ has typically employed tasks that have salient memory demands—asking for responses after the relevant objects have disappeared. This raises the possibility that these effects might reflect memory dynamics per se, rather than biases of spatial representation itself. The current studies thus employ both a placement task (in which observers simultaneously see two differently sized shapes, one of which has a dot in it, and then must place a second dot in the other shape so that their relative locations are equated) and a matching task (in which observers simultaneously see two dots, each inside a separate shape, and must simply report whether their relative locations are matched). Second, we ask whether spatial biases of this sort require bounding shapes in the first place. To that end, we use these tasks not only with common geometric shapes, but also in a ‘shapeless’ configuration with only a central landmark.

Collectively, these studies are thus intended to help reveal the nature of the simplest possible spatial biases—in particular (a) whether they only arise in more complex tasks, or might also appear even in perception tasks, with minimal memory demands, and (b) whether they are driven by shape-specific processing, or might also reflect how spatial representation differs for different regions and dimensions of space itself. The eight experiments below employ both the placement and matching tasks in the context of (a) shapes with clearly defined symmetry axes (such as squares and triangles; Experiments 1, 2a, and 2b), (b) a shape with no prioritized symmetry axes (i.e., a circle; Experiments 3a, 3b, and 3c), and (c) a ‘shapeless’ configuration with no bounding shape at all (Experiments 4a and 4b).

Experiment 1: Square placement (an initial demonstration)

Observers completed an especially simple task. On each trial, they saw two squares of different sizes, presented simultaneously on the screen—and inside one of the squares there was a small black dot. Observers simply had to place a second dot in that same relative location inside the other square (see Fig. 1a). Would systematic spatial biases still emerge in this task?

Fig. 1

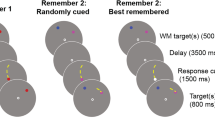
An example display from (a) the placement task (Experiments 1, 2a, 3a, and 4a) and (b) the matching task (Experiments 2b, 3b, 3c, and 4b). In the placement task, observers saw a dot inside one shape and had to place a corresponding dot inside another differently sized shape so that their relative locations were equated. In the matching task, observers saw two dots, each inside of differently sized shapes, and had to report whether those two dots were in the same relative location or not. These tasks were conducted with several different shapes. The colors here depict those from the actual displays, which varied slightly across the experiments

Method

Preregistrations and raw data for this experiment and each subsequent experiment can be accessed at https://osf.io/7asuw/

Participants

Ten naïve observers from the Yale/New Haven community completed the experiment in exchange for course credit or a small monetary payment. This preregistered sample size was chosen before data collection began based on independent pilot data, and was fixed to be identical for each of the eight experiments reported here. A power analysis confirmed that this sample size would have >99% power to detect an effect size of that obtained from independent pilot data in the first-reported analysis below. This pilot experiment had a similar design, except that observers completed half as many trials, and the initial locations of the dots (as described below) were randomly generated instead of being evenly distributed. In practice, this sample size gave us an average of >98% power to detect the effect sizes of the first-reported contrast below, across all of the Placement experiments reported here. This study was approved by the Yale University Institutional Review Board.

Apparatus

The experiment was conducted with custom software written in Python with the PsychoPy libraries (Peirce et al., 2019). Observers sat without restraint approximately 60 cm from a 43° × 25° display, with all spatial extents reported below computed based on this distance.

Stimuli

The display on each trial consisted of two white squares (each with a black border) on a grey (50% white, 50% black) background. One square was 9.54° (with a border stroke width of 0.09°), and the other was half that size (4.77°, with a border stroke width of 0.045°). The two squares appeared in opposite corners (counterbalanced across the four possible configurations). The smaller square’s center was 13.40° from the nearest horizontal border of the display, and 9.62° from the nearest vertical border of the display. For the larger square, these values were respectively 8.00° and 3.50°. In one of the squares (the small square on half of trials; the large square on the other half; blocked with order counterbalanced across observers as described below), there was a black dot (0.36° diameter in the larger square, 0.18° in the smaller square), whose location was randomly determined, with the constraints that no dot’s center could be closer than 0.22° from the border, and no two dots’ centers could be closer than 0.25°. A different set of random locations was determined for each observer, with the same set scaled to use for each square size. The dot locations used across all observers are depicted in Fig. 2a. The dot placed in the other shape by the observers (as described below) was identical to the visible dot, except that it was half the diameter (in the smaller square) or twice the diameter (in the larger square).

Fig. 2

Results from the placement experiments (Experiments 1, 2a, 3a, and 4a). On the far-left side (a, d, g, j) are the 3,200 random but evenly distributed dots initially shown to 10 different observers (320 dots each). In the middle column (b, e, h, k) are the observers’ placement responses. On the far right (c, f, i, l) are the same dots in the middle panel, filtered based on their local density so as to reveal the most salient patterns (as described in detail in the main text). The anchor disc in the shapeless figure (j-l) is not to scale, but is increased in size here for visibility. The correspondence between the dots in the left and middle columns is revealed in the online animations corresponding to each row, available at http://perception.yale.edu/SpatialBiases/

Procedure

On each trial, observers simply had to place the second dot in the same relative location inside the empty square, by moving and then clicking the mouse. The second dot appeared at a mouse click, at which point observers could click additional times or drag and drop the dot to change its location. Once observers were satisfied with the second dot’s location, they pressed a key to submit their response—with responses only accepted within the square’s boundary. If a response was recorded, then the display was replaced with a blank screen for a randomly chosen interval of 0.5–1.5s, after which the next trial began. If no response was recorded within 5 s, then a warning to respond more quickly appeared for 5 s before the next trial began, and that trial was randomly shuffled back into the trial sequence.

Design

Each observer completed 320 trials, divided into two equal blocks: 160 small-to-large trials (i.e., with the initially present dot in the smaller square), and 160 large-to-small trials (i.e., with the initially present dot in the larger square). The same set of locations (as described above) was used in each block, but in a different randomized order, and the order of the blocks was counterbalanced across observers. Between the two blocks, a message appeared encouraging observers to rest briefly before continuing, and they were instructed to press a key whenever they were ready to begin the next block. Observers completed four representative practice trials (the data from which were not recorded) before beginning the task.

Results

The raw locations in which observers placed their dots are presented in Fig. 2b. This figure depicts only the resulting distribution of dots, but in the corresponding online animation (available for each Placement experiment at http://perception.yale.edu/SpatialBiases/), each initial dot moves to its corresponding placed location—thus making it clear which dot in Fig. 2a corresponds to which dot in Fig. 2b. Even without viewing the online animations, however, inspection of the distributions in Fig. 2b reveals a salient systematic pattern: Dots appear to be biased away from the square’s horizontal and vertical axes, thus giving rise to ‘clumps’ of dots within each of the square’s four quadrants. This quadrant-like structure is then made especially apparent in the ‘filtered’ visualizations presented in Fig. 2c. This figure presents the same dots from Fig. 2a, but now filtered for local density—removing all dots that had fewer than 55 neighboring dots within a 30-pixel radius—to visually reveal the underlying clustering. (This and subsequent visualizations are not meant to serve as formal analyses, but rather to help intuitively convey the patterns reported below.) The resulting clumps of dots are clearly located around the centers of the four quadrants. This bias is also readily apparent in Fig. 3b, wherein the angular displacement errors (presented along the vertical axis) are plotted according to the dots’ initial angular positions (presented along the horizontal axis). In this figure, each point represents a single trial. The horizontal axis ranges from 0° to 360°, where 0° represents the initial angular position at what would be “South” on a compass, and angles increases counterclockwise (so that, e.g., a dot to the right of the square’s center would be at 90°, and a dot above the square’s center would be at 180°). The angular displacement was calculated by subtracting the initial dot’s angular position from the response dot’s angular position. This figure reveals a clear ‘sawtooth’ pattern, wherein the direction of the dominant angular bias switches suddenly at each quadrant boundary.

Fig. 3

Additional results from the placement experiments (Experiments 1, 2a, 3a, and 4a). The left column (a, d, g, j) depicts the relevant shape/experiment. The middle column (b, e, h, k) depicts the errors in angular space for each of the 3,200 dots—with the angular displacement errors (presented along the vertical axis) plotted according the dots’ initial angular positions (presented along the horizontal axis, with 0° at the bottom of the shape and the angles increasing counterclockwise). These graphs reveal a clear ‘sawtooth’ pattern, wherein the direction of the dominant angular bias switches suddenly at each quadrant (or ‘trirant’) boundary. The right column (c, f, i, l) depicts the degree to which each observer’s placements were biased towards versus away from the nearest oblique axis—and as such it captures how robust these effects were across observers

These impressions were confirmed by the following analyses.¹ We first demonstrated these patterns in the most straightforward way possible, by simply asking how many of the dots were placed towards the nearest oblique axis in angular space (i.e., the NE, NW, SE, and SW compass directions). Indeed, a majority (M = 61.9%, SD = 8.2%) of the placed dots were biased towards the nearest oblique axis, t(9) = 4.62, p = .001, d = 1.46. (This was a one-sample t test comparing the average percentage of dots that were displaced towards the nearest oblique axis to the chance level of 50%. Throughout this paper, d refers to the classical Cohen’s d). And this was independently true for nine of the 10 observers (as depicted in Fig. 3c). This analysis included a dot even if it was placed outside the 45° sector that contained the initially presented dot—thus including trials in which a placed dot was biased not only toward but beyond the nearest oblique axis. In practice, however, excluding such trials yielded a qualitatively identical pattern: 62.7% (SD = 9.0%) of placed dots were biased towards the nearest oblique axis—t(9) = 4.47, p = .002, d = 1.41—and this was similarly true for all subsequent Placement experiments.

In addition to asking about the direction of errors, we also assessed their magnitudes. In particular, we asked whether dots that were biased towards the nearest oblique axis had a larger displacement error than did the other dots (again including only those dots that were placed in the same 45° sector that housed their original dots, which retained 2,762 of the 3,200 trials—with dots placed exactly on an axis counted as being in a different sector). Again, there was a clear bias: Dots placed towards the nearest oblique axis were displaced by an average of 6.44° (SD = 1.47°), whereas other dots were displaced by an average of 4.05° (SD = 1.00°), t(9) = 6.67, p < .001, d = 2.11. And in a complementary fashion, dots that originated farther from the oblique axes were displaced to a greater degree than were dots that originated closer to these axes. This was apparent from the systematic locations of the most extreme points of the ‘sawteeth’ in Fig. 3b, and it was verified by a reliable negative correlation across observers between the position within a quadrant (e.g., starting at any cardinal axis, and the angles increasing counterclockwise, collapsing across quadrants, such that all the points are in a 0°–90° space) and the signed error in the angular dimension (r_M = –.204, r_SD = .125), t(9) = 5.17, p = .001, d = 1.63.

Finally, whereas the previous analyses served to verify the patterns that were apparent from the figures themselves, we can also derive and quantify the fundamental angular pattern of biases without making any figure-driven assumptions. In particular, we can measure the density of each thin spatial slice of the data, and then ask which patterns emerge. Table 1a simply presents counts of the raw numbers of dots placed within each 10° sector of the square, sorted by dot count (with 0° starting at what would be “South” on a compass, and angles increasing counterclockwise; i.e., 0°–10°, 10°–20°, etc.). To make the resulting patterns clear, we then color-coded these 36 sectors as follows: (a) sectors containing a cardinal axis are dark blue; (b) sectors adjacent to a sector containing a cardinal axis are light blue; (c) sectors containing an oblique axis are dark red, and (d) sectors adjacent to a sector containing an oblique axis are light red. Notice that there are twice as many dark-blue sectors as there are dark-red sectors; this is because each oblique axis ends up centered in one of the 10° sectors, whereas each cardinal axis falls in between a pair of sectors. Here, we will refer to the darker-colored sectors (alone) as the Narrow Band sectors, and the lighter-colored sectors (alone) as the Wide Band sectors. Note that the Wide Band sectors do not contain the Narrow Band sectors. All sectors are equal in size, and the Wide Band sectors simply refer to those that are slightly farther away from the relevant axes.

Table 1 Mean number of dots in each sector, rank ordered by dot count for each shape from highest to lowest

Table 1a supplements the prior analyses, effectively verifying, quantifying, and qualifying the quadrant-like pattern that is apparent from Fig. 2b, in three ways. First, note that oblique sectors contain many more dots than do cardinal sectors. And this is true for both the Narrow Bands (14.65 [SD = 2.77] vs. 5.65 [SD = 1.03]), t(9) = 9.50, p < .001, d = 3.00, and the Wide Bands (13.21 [SD = 1.21] vs. 5.06 [SD = 1.31]), t(9) = 11.16, p < .001, d = 3.53. Second, the dot counts varied extremely systematically with these Narrow and Wide Band categories considered together: The 12 oblique sectors were exactly the 12 sectors that had the most dots (as in the unbroken red region at the top of this table); the 16 cardinal sectors were exactly the 16 sectors that had the fewest dots (as in the unbroken blue region at the bottom of this table); and therefore (a) no oblique sector had fewer dots than any other sector (cardinal or otherwise), and (b) no cardinal sector had more dots than any other sector (oblique or otherwise). Third, these placement patterns were not especially tightly clustered around the relevant axes: Narrow Band sectors had more dots on average than did Wide Band sectors, but this difference is not reliable for either oblique sectors (14.65 vs. 13.21), t(9) = 1.81, p = .10, d = 0.57, or cardinal sectors (5.65 vs. 5.06), t(9) = 1.05, p = .32, d = 0.33, and the Narrow and Wide Band sectors were generally interleaved (as is readily apparent from the fact that the dark colors did not perfectly cluster together at the top and bottom of this table). For example, notice that the second-densest sector (210°–220°) and the two least dense sectors (10°–20°, 190°–200°) were both Wide Band sectors.

Discussion

Despite using such a simple task with minimal memory demands, this experiment revealed a salient systematic spatial bias, in which dots were displaced toward their nearest oblique axes (and thus away from their nearest cardinal axes, and toward the centers of their surrounding quadrants). This pattern can be appreciated in Fig. 2b by noting the salient white (i.e., low-density) horizontal and vertical ‘stripes’, and it can be even better appreciated in the corresponding online animation by noting the salient exodus from the cardinal axes. And as explored in detail in the General Discussion, this pattern was highly reminiscent of the biases that are observed in tasks with greater memory demands (e.g., Huttenlocher et al., 1991; Langlois et al., 2017).

Experiment 2a: Triangle placement (shape-specific biases?)

Where did the powerful quadrant-like structure revealed in Experiment 1 originate? It could somehow reflect some deep aspect of spatial representation itself, but it could also just reflect the fact that squares (i.e., quadrangles) can so naturally be represented as having quadrants. We explored this in the subsequent experiments, first focusing on the latter possibility that these effects are intrinsically shape specific: If the quadrant-like structure depended on the square per se, then it should change dramatically if we conduct the same test on a different shape, such as a triangle.

Method

This experiment was identical to Experiment 1, except as noted. Ten new observers participated, with this sample size chosen to match that of Experiment 1. The display consisted of two equilateral triangles rather than two squares. The circumcircle of the larger triangle had a radial extent (i.e., from the center to the outermost edge) of 8.96°, and the smaller triangle was exactly half this size. This size was chosen so that the areas of the triangles were roughly equated to those of the squares in Experiment 1. The grey background was 25% black and 75% white. The dot locations used across all observers are depicted in Fig. 2d.

Results

The raw locations in which observers placed their dots are presented in Fig. 2e, and the correspondence with the dots in Fig. 2d is made clear in the corresponding online animation. Inspection of the distributions in Fig. 2e reveals a salient systematic pattern, which reflects the shape itself, and which is noticeably different from the quadrant-like structure observed in Experiment 1. In particular, if the triangle is divided into three regions by drawing dividing lines from the midpoints of (and perpendicular to) each side to the triangle’s center, then the dots placed by observers appear to be biased towards the centers of those three regions (which we might call ‘trirants’, by analogy to the quadrant-like structure in Experiment 1). This structure is then made especially apparent in the ‘filtered’ results presented in Fig. 2f. And this bias is also readily apparent in Fig. 3e, which again reveals a sawtooth pattern in which the direction of the dominant angular bias switches suddenly at each ‘trirant’ boundary.

These impressions were confirmed by the following analyses. A majority (M = 57.0%, SD = 5.2%) of the dots were placed towards the lines joining the angle tips and the triangle’s centroid, t(9) = 4.24, p = .002, d = 1.34, and this was independently true for all 10 observers (as depicted in Fig. 3f). Dots that were biased towards the nearest axis also had a larger displacement error than did the other dots (again including only those dots that were placed in the same region that housed their original dots, which retained 2,761 of the 3,200 trials): 8.67° (SD = 0.79°) vs. 5.78° (SD = 1.01°), t(9) = 5.63, p< .001, d = 1.78. And in a complementary fashion, dots that originated farther from the axes joining the angle tips and the centroid were displaced to a greater degree than were dots that originated closer to these axes. This was apparent from the systematic locations of the most extreme points of the ‘sawteeth’ in Fig. 3e, and it was verified by a reliable negative correlation across observers between the position within a trirant (e.g., starting at any medial axis, and the angles increasing counterclockwise, collapsing across trirants, such that all the points are in a 0°–120° space) and the signed error in the angular dimension (r_M = –.145, r_SD = .085), t(9) = 5.42, p < .001, d = 1.71.

The fact that this ‘trirant’ structure fits the present data better than does the ‘quadrant’ structure from Experiment 1 is readily apparent from Figs. 2e, f, and 3e. But this can also be quantified: In fact, there were more dots displaced towards the relevant axes of the triangle than there were displaced towards the (irrelevant) oblique axes of the square (57.0% [SD = 5.2%] vs. 50.7% [SD = 3.8%]), t(9) = 3.43, p = .007, d = 1.09. And similarly, we can retroactively show that more dots in Experiment 1 were displaced towards the oblique axes of the square than were displaced towards the (irrelevant) axes of the triangle: 61.9% (SD = 8.2%) vs. 47.5% (SD = 3.5%), t(9) = 5.86, p < .001, d = 1.85.

Finally, we can also again derive the fundamental pattern of angular biases without making any figure-driven assumptions. Table 1b presents counts of the raw numbers of dots placed within each 10° sector of the triangle, sorted by dot count. This table effectively verifies, quantifies, and qualifies the same trirant pattern that is so apparent from Fig. 2e. In particular, the same kinds of patterns that we previously noted for the Square in Experiment 1a are again apparent here: First, sectors along the medial axes contained many more dots than do sectors along the opposite axes. And this was true for both the Narrow Bands (18.60 [SD = 2.13] vs. 4.77 [SD=0.64]), t(9) = 18.42, p < .001, d = 5.82, and the Wide Bands (12.70 [SD = 1.72] vs. 3.73 [SD = 1.20]), t(9) = 10.90, p < .001, d = 3.45. Second, the dot counts again varied extremely systematically with these Narrow and Wide Band categories considered together: The 12 medial axis sectors were exactly the 12 sectors that had the most dots (as in the unbroken red region at the top of this table), and of the 14 sectors with the fewest dots, 10 of them were sectors on or near the opposite axes (as in the nearly unbroken blue region at the bottom of this table). Third, these placement patterns were tightly clustered around the relevant medial axes (with the Narrow and Wide band sectors perfectly segregated—as is apparent from the fact that the dark red sectors all lie at the very top of this table), but not around the opposite axes (with the Narrow and Wide band sectors generally interleaved—as is apparent from the fact that the dark blue sectors did not lie at the very bottom of this table). For example, notice that none of the four least-dense sectors were Narrow Band sectors.

Discussion

This experiment again revealed salient systematic biases even in such a simple task. In one sense, these biases were critically different from those in Experiment 1—now seeming to reflect the bounding triangle shape per se, rather than having a quadrant-like structure. But in another sense, the results were identical—insofar as each resulting dot ‘clump’ in both experiments appears to be roughly centered on the center of a corresponding ‘branch’ of the relevant shape’s medial-axis skeleton (a specific type of symmetry axis—including all internal points equidistant from two or more points along the shape’s bounding contour— thought to be involved in how we recognize shapes; e.g., Feldman & Singh, 2006; Firestone & Scholl, 2014; Lowet, Firestone, & Scholl, 2018). These medial-axes are depicted explicitly in Fig. 2c and f by the thin dashed lines. Both observations suggest a type of shape-specific effect, and they emphasize how the nature of the bounding shape can play a critical role in the biases that are observed in this task.

Experiment 2b: Triangle matching (shape-specific biases?)

The previous experiments employed a simple task, but it did involve an active ‘placement’ action. Might the existence of robust spatial biases somehow depend on this unusual task? To find out, we also measured biases in a matching task that was also simple (and that also featured all of the relevant information on the display simultaneously, to minimize memory demands), but that didn’t involve any ‘placements’. Observers saw two dots inside of two differently sized triangles, and simply had to report whether those two dots were in the same relative location or not. Would observers again be systematically biased, such that they are more accurate at recognizing some types of deviations than others?

Method

This experiment was identical to Experiment 2a, except as noted. Ten new observers participated, with this sample size chosen to match those of Experiments 1 and 2a. In practice, it gave us an average of >99% power to detect the effect sizes of the first-reported contrasts below, across all of the Matching experiments—except for Experiment 3c, where it gave us only 57.9% power to detect that same contrast.

The smaller triangle always appeared in the upper-left corner, and the larger triangle always appeared in the lower-right corner. The smaller triangle’s centroid was 13.40° from the nearest horizontal border of the display, and 8.90° from the nearest vertical border of the display. For the larger triangle, these values were respectively 8.00° and 3.50°. The shapes were grey (50% white and 50% black) with a solid black outline (with border stroke widths of 0.045° and 0.09°). Inside both triangles, there was a dot (diameter 0.27° in the smaller triangle, 0.54° in the larger triangle). Across trials, the upper-left dot always appeared along invisible radial lines every 60° from the triangle’s centroid (i.e., at 0°, 60°, 120°, etc.), halfway between the center and the outer edge—with these six possible dot locations depicted in Fig. 4c. The lower-right dot was in the same location on 20% of trials, and was displaced from this position on the remaining 80% of trials. These displacements occurred either (a) by retaining the distance of the dot from the centroid, but changing its angular direction from the centroid (by 4°, 8°, 12°, or 16°—moving either clockwise or counterclockwise), as depicted in Fig. 4a, or (b) by retaining the angular direction of the dot, but changing its distance from the centroid (by 0.22°, 0.44°, 0.66°, or 0.88°—moving either inward or outward), as depicted in Fig. 4b.² These different types of changes occurred in equal counterbalanced numbers, presented in a different random order for each observer.

Fig. 4

Results from the matching experiments (Experiments 2b, 3b, 3c and 4b). a–b Depictions of the two kinds of changes (in angle or distance) used in these experiments. c–e Spatial errors for the triangle. f–h Spatial errors for the circle. i–k Spatial errors for the shapeless configuration. l–n Spatial errors for the rotated circle configuration. The left column (c, f, i, l) depicts the relevant shape/experiment, with color-coded axes, and with black dots indicating the possible locations of the dots that appeared in the upper-left shape. The middle column (d, g, j, m) depicts errors across several degrees of angle change, broken down by the relevant axes (excluding m, where there are no different axes). The right column (e, h, k, n) depicts errors across several levels of distance change (in visual angles). Error bars represent between-subject standard errors

The task was simply to report (with no time limit, via a dichotomous key press on a standard keyboard: ‘s’ for same, ‘d’ for different) whether the two dots were in the same relative location in their respective triangles. Each observer completed 240 trials. Forty-eight were No-Change trials: six initial upper-left dot positions (i.e., 6 possible angles [as depicted by the 6 dots in Fig. 4c] × 4 repetitions × 2 blocks. The remaining 192 were Change trials: the same 6 initial upper-left dot positions × 8 possible displacements (4 angular displacements + 4 distance displacements) × 2 directions of change (left/right or in/out) × 2 blocks. The Change and No-Change trials were evenly distributed throughout the two blocks. Observers completed 10 representative practice trials (the data from which were not recorded) before beginning the task.

Results

Matching accuracy is depicted in Fig. 4, broken down both by angular changes (Fig. 4d) and distance changes (Fig. 4e), and by changes originating both on medial-axis segments (in red) and by other symmetry axes joining the center of each side to the triangle’s centroid (in blue). In each case, the vertical axis represents the percentage of trials in which observers perceived the two dots as having the same relative location, and the horizontal axis represents the actual magnitude of the difference. As such, we expect peak ‘% Same’ ratings in the center (i.e., when the two dots actually did share the same relative locations), with the tails falling off on either side of this peak. Inspection of these results reveals a clear dissociation: For angle changes, observers performed better for dots originating on medial-axis segments (relative to matched angle changes at the opposite axes), in the sense that the red data points were on average lower than the blue data points in Fig. 4d for the non-0° change magnitudes (15.6% [SD = 5.3%] vs. 69.6% [SD = 20.7%]), t(9) = 8.16, p < .001, d = 2.58. But this pattern reversed (with worse performance for dots originating on medial-axis segments) for distance changes, in the sense the red data points were on average higher than the blue data points in Fig. 4e for the non-0-px change magnitudes (68.8% [SD = 13.7%] vs. 50.4% [SD = 15.8%]), t(9) = 6.61, p < .001, d = 2.09. And, indeed, there was also a reliable interaction between these factors, t(9) = 8.92, p < .001, d = 2.82.

Discussion

These results again suggest biases that seem specific to the shape itself—insofar as performance depended on both (a) angular changes versus distance changes, and (b) the shape-specific region in which one of the dots originated (i.e., along the medial axes vs. the opposite axes). In particular, this apparent dependence on the type of axis is the same factor that seemed to influence the placement effects in Experiment 2a. Here, in addition, these matching results suggest that the resolution of spatial representation itself might differ for different regions and dimensions of the shape. But this suggestion must remain only tentative for now, because the two types of axes had notably different lengths (with the medial axes—in red in Fig. 4c—being twice as long). We nevertheless report these results here so that they can be compared with the later matching results with other cases (corresponding to the other rows in Fig. 4) in which this confound is not present. And, so, the only key conclusion we draw for now from the present experiment is that some systematic spatial biases emerge even in a task that does not require overt placement.

Experiment 3a: Circle placement (biases without prioritized shape axes?)

So far, all of the spatial biases seem attributable in principle to the nature of the bounding shapes. For example, the ‘trirant’-like placement results (from Experiment 2a, depicted in Fig. 2e and f) may reflect the bounding triangle, while the quadrant-like placement results (from Experiment 1, depicted in Fig. 2b and c) may reflect the bounding quadrangle: In both cases, each higher-density ‘clump’ of dots seems roughly centered over the center of a corresponding medial-axis branch. Does this mean that all such systematic biases are shape specific? Or might there also be reliable biases even without any prioritized shape axes? To find out, we employed the placement task with a circle—which does not have any angles or sides that could somehow prioritize different regions—and which by definition has no medial-axis branches at all.

Method

This experiment is identical to Experiment 1, except as noted. Ten new observers participated, with this sample size chosen to match those of each of the three previous experiments. The displays consisted of two circles rather than two squares. The larger circle had a radius of 5.4°, and the smaller circle was half this size. This size was chosen so that the areas of the circles were roughly equated to those of the squares in Experiment 1. The dot locations used across all observers are depicted in Fig. 2g.

Results

The raw locations in which observers placed their dots are presented in Fig. 2h, and the correspondence with the dots in Fig. 2g is made clear in the corresponding online animation. Inspection of the distributions in Fig. 2h reveals a salient systematic pattern, which reflects the same quadrant-like structure observed in Experiment 1 (as is apparent, for example, from the salient white lower-density vertical and horizontal stripes in this image)—despite the lack of any distinguishable bounding contours or angles. This structure is then made especially apparent in the ‘filtered’ results presented in Fig. 2i. This bias is also readily apparent in Fig. 3h, which again reveals a clear sawtooth pattern in which the direction of the dominant angular bias switches suddenly at each quadrant boundary.

These impressions were confirmed by the following analyses. A majority (M = 66.0%, SD = 4.5%) of the dots were placed towards the nearest oblique axis, t(9) = 11.21, p < .001, d = 3.55, and this was independently true for all 10 observers (as depicted in Fig. 3i). Dots that were biased towards the nearest axis also had a larger displacement error than did the other dots (again including only those dots that were placed in the same region that housed their original dots, which retained 2,615 of the 3,200 trials): 7.70° (SD = 1.16°) versus 5.16° (SD = 0.67°), t(9) = 10.46, p < .001, d = 3.31. And in a complementary fashion, dots that originated farther from the oblique axes were displaced to a greater degree than were dots that originated closer to these axes. This was apparent from the systematic locations of the most extreme points of the ‘sawteeth’ in Fig. 3h, and it was verified by a reliable negative correlation across observers between the position within a quadrant and the signed error in the angular dimension (r_M = –.251, r_SD = .113), t(9) = 7.00, p < .001, d = 2.21.

This quadrant-like structure fit the placement data better than did the trirant-like structure from Experiment 2a (as is clear from Figs. 2h, i, and 3h): There were more dots displaced towards the relevant oblique axes than there were placed towards the (irrelevant) axes of the triangle (66.0% [SD = 4.5%] vs. 51.2% [SD = 3.7%]), t(9) = 7.15, p < .001, d = 2.26.

Finally, we can also again derive the fundamental pattern of angular biases without making any figure-driven assumptions. Table 1c presents counts of the raw numbers of dots placed within each 10° sector of the circle, sorted by dot count. This table effectively verifies, quantifies, and qualifies the same quadrant-like pattern that is so apparent from Fig. 2h. In particular, the same three patterns that we previously noted for the Square in Experiment 1a are again apparent here: First, oblique sectors again contained many more dots than did cardinal sectors. And this was true for both the Narrow Bands (12.38 [SD = 1.11] vs. 6.58 [SD = 1.01]), t(9) = 11.56, p < .001, d = 3.66, and the Wide Bands (11.43 [SD = 1.55] vs. 7.03 [SD = 1.07]), t(9) = 5.49, p < .001, d = 1.74. Second, the dot counts again varied extremely systematically with these Narrow and Wide Band categories considered together: The 12 oblique sectors were exactly the 12 sectors that had the most dots (as in the unbroken red region at the top of this table); 14 of the 16 cardinal sectors were the 14 sectors that had the fewest dots (as in the nearly unbroken blue region at the bottom of this table, with the only exceptions being the two Wide Band sectors of 10°–20° and 160°–170°), and therefore (a) no oblique sector had fewer dots than any other sector (cardinal or otherwise), and (b) only two of the 16 cardinal sectors had more dots than any other sector, and none had more dots than any oblique sector. Third, these placement patterns were again not especially tightly clustered around the relevant axes, as the Narrow and Wide band sectors were generally interleaved (as is apparent from the fact that the dark colors did not perfectly cluster together at the top and bottom of this table). For example, notice that the third-densest and fourth-densest sectors [320°–330°, 140°–150°] and the least dense sector [70°–80°] were all Wide Band sectors.

Discussion

Empirically, the results of this experiment were familiar: They revealed the same qualitative pattern that was observed with the square in Experiment 1. But theoretically, these results are both novel and surprising—because here this quadrant-like structure emerged without any possible bias from specific contours or angles of the surrounding shape. And whereas the ‘filtered’ dot clumps in both previous placement experiments were each roughly centered on a medial-axis branch, that is not true here—because a circle has no medial axis branches. So, these results fuel an importantly different conclusion: Quadrant-like spatial biases may not arise from the details of the bounding shape at all, but rather may reflect differences in spatial representation itself.

Experiment 3b: Circle matching (biases without prioritized shape axes?)

We next asked whether spatial biases with a circle would also manifest themselves in the matching paradigm.

Method

This experiment was identical to Experiment 2b, except as noted. Ten new observers participated, with this sample size chosen to match those of the previous four experiments. The displays consisted of two circles rather than two triangles. The larger circle had a radius of 4.3°, and the smaller circle was half that size. Across trials, the upper-left dot always appeared along invisible radial lines every 45° from the circle’s center (i.e., at 0°, 45°, 90°, etc.), halfway between the center and the outer edge—with these eight possible dot locations depicted in Fig. 4f. Each observer completed 320 trials. Sixty-four were No-Change trials: 8 initial upper-left dot positions (i.e., 8 possible angles, as depicted by the dots in Fig. 4f) × 4 repetitions × 2 blocks. The remaining 256 were Change trials: the same 8 initial upper-left dot positions × 8 possible displacements (4 angular displacements and 4 distance displacements) × 2 directions of change (left/right or in/out) × 2 blocks.

Results

Matching accuracy is depicted in Fig. 4g and h, broken down as in Experiment 2b. Inspection of these results reveals a clear dissociation for angle changes, in the opposite direction from that observed in Experiment 2b: Observers made more errors for dots near oblique axes, relative to dots near cardinal axes (62.5% [SD = 11.5%] vs. 43.0% [SD = 13.8%]), t(9) = 7.32, p < .001, d = 2.31. However, no reliable difference was observed for distance changes (61.1% [SD = 15.1%] vs. 57.5% [SD = 12.3%]), t(9) = 1.20. p = .26, d = 0.38. And once again, there was also a reliable interaction between these factors, t(9) = 5.65, p < .001, d = 1.79.

Discussion

The key result from this experiment is the same one that was apparent in Experiments 1 and 3a: There appears to be something special about the oblique (vs. cardinal) regions of space. This was revealed in the placement task (in Experiments 1 and 3a) by the displacement of dots toward these axes, and it was apparent in the current experiment in terms of worse performance at discriminating angle changes in these regions. The fact that this occurred even with the matching task using a circle suggests that such patterns reflect something fundamental about spatial representation, in ways that do not depend on (a) prioritized angles or edges (as in Experiments 1 and 2), (b) active placement actions (as in Experiments 1 and 3a), or (c) axes of different lengths (as was the case for the triangle-matching task in Experiment 2b).

Experiment 3c: Rotated circle matching (biases without prioritized shape axes?)

The initial dots in the upper-left circle in Experiment 3b each fell along either a cardinal or oblique axis (as depicted in Fig. 4f). Could this fact have somehow given rise to the oblique versus cardinal difference observed in the results of that experiment? To find out, we replicated Experiment 3b, but now the initial dots were rotated by 22.5° so that no dots would initially lie along a major axis (as depicted in Fig. 4l). Would the results still indicate a special role for oblique versus cardinal regions?

Method

This experiment was identical to Experiment 3b, except as noted. Ten new observers participated, with this sample size chosen to match those of the previous five experiments. The invisible radial lines along which the upper-left dots appeared were shifted 22.5° relative to Experiment 3b (i.e., so that the dots appeared at 22.5°, 67.5°, 112.5°, etc.).

Results

Matching accuracy is depicted in Fig. 4m and n, broken down as in the previous experiments. Here, however, the relevant comparison is not a difference between the two axes—because all eight axes were halfway between oblique and cardinal axes. Instead, the relevant comparison is between those points that were offset towards versus away from the oblique axes. Analogous to the results in Experiments 2b and 3b, observers again made more errors at discriminating angle changes for dots offset towards oblique axes, relative to dots offset towards cardinal axes (55.5% [SD = 17.6%] vs. 42.2% [SD = 16.1%]), t(9) = 2.47, p = .04, d = 0.78. This is apparent in Fig. 4m by the fact that the points on the right side of the graph are lower than are those on the left side. There was no analogous comparison we could make in this experiment for distance changes, but we also compared performance for dots offset outward versus inward—and this did not reveal any reliable difference (47.8% [SD = 16.0%] vs. 40.8% [SD = 7.3%]), t(9) = 1.58, p = .15, d = 0.50.

In contrast, if we simply take the two sets of ‘rotated’ axes as given, we find no differences. In particular, when we arbitrarily categorized one set of axes as ‘oblique’ (22.5°, 112.5°, 202.5°, and 292.5°) and one as ‘cardinal’ (67.5°, 157.5°, 247.5°, and 337.5°), there were no differences between these two sets of axes for either angle changes (47.0% [SD = 19.7%] vs. 50.6% [SD = 10.5%]), t(9) = 0.92, p = .38, d = 0.29, or distance changes (42.7% [SD = 12.0%] vs. 45.9% [SD = 8.3%]), t(9) = 1.58, p = .15, d = 0.50, and there was no interaction between these factors, t(9) = .09, p = .93, d = 0.03.

Discussion

Even when the initial dots did not lie on a cardinal or oblique axis, observers were still worse at discriminating angle changes near the oblique (vs. cardinal) regions. This suggests that the effect observed both here and in Experiment 3b reflects something about spatial representation itself, rather than being an artifact of the experimental design.

Experiment 4a: Shapeless placement (purely spatial biases?)

Experiments 3a, 3b, and 3c revealed angular spatial biases in the absence of any prioritized angles or contours, suggesting that these biases reflect the nature of spatial representation, per se, rather than reflecting something specific to shape perception. Here, we attempted to push this even further, by eliminating the bounding shape altogether in the placement task: Observers simply saw and placed dots relative to a small central anchor disc (see Fig. 2j). This also tests whether spatial biases occur in the absence of a size-translation manipulation, because, of course, that is not possible without a bounding shape.

Method

This experiment is identical to Experiment 3a, except as noted. Ten new observers participated, with this sample size chosen to match that of the previous six experiments. Rather than two circles, both corners simply contained a central black ‘anchor’ disc, with a 0.13° diameter and no outline. On each trial, a white dot (0.26° diameter) was presented near one of the anchor discs, with its location determined across trials as in Experiment 3a (i.e., as if the bounding shape were the larger circle). The dot locations used across all observers are depicted in Fig. 2j. The task was then to place a second white dot (of the same size) in the same relative location (now without any size transformation), near the other anchor disc.

Results

The raw locations in which observers placed their dots are presented in Fig. 2k, and the correspondence with the dots in Fig. 2j is made clear in the corresponding online animation. Note that some of the placed dots in this figure appear slightly outside the invisible bounding circle. This was not true in the previous placement experiments, because responses were not accepted if they fell outside the bounding shape—but here there was no bounding shape, and so dot placements were accepted no matter where they fell. Inspection of the distributions in Fig. 2k reveals a salient systematic pattern, which again clearly reflects the same quadrant-like structure observed in Experiments 1 and 3a (again, with the salient white lower-density vertical and horizontal stripes), even though there was no visible bounding shape at all in this experiment. This structure is then made especially apparent in the ‘filtered’ results presented in Fig. 2l. This bias is also readily apparent in Fig. 3k, which again reveals a slightly messier sawtooth pattern in which the direction of the dominant angular bias switches suddenly at each quadrant boundary.

These impressions were confirmed by the following analyses. A majority (M = 62.3%, SD = 7.9%) of the dots were placed towards the nearest oblique axis, t(9) = 4.95, p < .001, d = 1.56, and this was independently true for all 10 observers (as depicted in Fig. 3l). Dots that were biased towards the nearest axis also had a larger displacement error than did the other dots (again including only those dots that were placed in the same region that housed their original dots, which retained 2,859 of the 3,200 trials): 5.53° (SD = 1.91°) versus 4.30° (SD = 1.30°), t(9) = 3.78, p = .004, d = 1.19. And in a complementary fashion, we can again assess whether dots that originated farther from the oblique axes were displaced to a greater degree than were dots that originated closer to these axes. This was again apparent from the systematic locations of the most extreme points of the ‘sawteeth’ in Fig. 3k, and it was verified by a reliable negative correlation across observers between the position within a quadrant and the signed error in the angular dimension (r_M = –.274, r_SD = .154), t(9) = 5.65, p < .001, d = 1.79.

This quadrant-like structure fit the placements better than did the trirant-like structure from Experiment 2a (as is clear from Figs. 2k, l, and 3k): There were more dots displaced towards the relevant oblique axes than there were placed towards the (irrelevant) axes of the triangle (62.3% [SD = 7.9%] vs. 50.2% [SD = 2.1%]), t(9) = 5.24, p = .001, d = 1.66.

A close inspection of the filtered placement results in Fig. 2l also suggests that the dots are more widely distributed than are the dots in Fig. 2i. This is apparent from the fact that the dots in Fig. 2i seem clumped much more closely around the oblique axes, whereas the low-density horizontal and vertical ‘stripes’ are much more well-defined in Fig. 2l than in Fig. 2i. And indeed, this impression was empirically supported: On average, more dots were placed within 10° of the oblique axes in the circle compared with the shapeless configuration (98.2 [SD = 10.3] vs. 78.9 [SD = 8.9]), t(18) = 4.50, p < .001, d = 2.01. However, we cannot draw any firm conclusions from this pattern, because it may merely reflect overall differences in accuracy: Because this experiment did not involve a size-translation component, observers may have simply matched the displays more exactly, yielding less of a bias towards the oblique regions.

Finally, we can also again derive the fundamental pattern of angular biases without making any figure-driven assumptions. Table 1d presents counts of the raw numbers of dots placed within each 10° sector of the shapeless configuration, sorted by dot count. This table effectively verifies, quantifies, and qualifies the same quadrant-like pattern that is apparent from Fig. 2k—although these patterns were generally noisier than in the previous experiments (just as Fig. 2k appears noisier than does either Fig. 2b or h). In particular, the same three patterns that we previously noted for the Square and the Circle (in Experiments 1a and 3a) are again apparent here: First, oblique sectors again contained more dots than did cardinal sectors—although unlike the prior experiments, this was true only for the Narrow Bands (9.78 [SD = 1.32] vs. 6.51 [SD = 1.48]), t(9) = 4.63, p = .001, d = 1.47, and not for the Wide Bands (10.14 [SD = 1.58] vs. 9.00 [SD = 1.20]), t(9) = 1.50, p = .17, d = 0.47. Second, the dot counts again varied systematically with these Narrow and Wide Band categories considered together, although this pattern was considerably noisier: Eight of the oblique sectors were still among the 11 sectors that had the most dots (as in the more diffuse concentration of red sectors at the top of this table); 10 of the cardinal sectors (including all eight Narrow Band sectors) were still among the 12 sectors that had the fewest dots (as in the concentration of blue sectors at the bottom of this table); and in general several oblique sectors had fewer dots than several cardinal sectors for the Wide Bands—although it was still the case for the Narrow Bands that no oblique sector had fewer dots than any cardinal sector, and vice versa. Third, these placement patterns were again not especially tightly clustered around the relevant axes, as the Narrow and Wide band sectors were generally interleaved. However, this pattern seemed to differ for the cardinal versus oblique sectors in this experiment. In particular, this clustering was much tighter for cardinal sectors (in which the seven least dense sectors were all Narrow Band sectors) than for oblique sectors (in which only one of the six densest sectors was a Narrow Band sector). Interestingly, this is the opposite pattern than that observed with the triangle in Experiment 2a—in which we observed much tighter clustering for the densest sectors compared with the least dense sectors.

Discussion

The results of this experiment reveal biases in spatial representation in the starkest way yet—because here the now-familiar quadrant-like structure emerged even without any bounding shape at all, and even without the size-translation manipulation.

Experiment 4b: Shapeless matching (purely spatial biases?)

In our final experiment, we asked whether spatial biases with a ‘shapeless’ configuration (as in Experiment 4a) would also manifest themselves in the matching paradigm.

Method

This experiment is identical to Experiment 3b, except as noted below. Ten new observers participated, with this sample size chosen to match those of the previous seven experiments. The grey background was 50% white and 50% black. Instead of a bounding shape, both corners contained a black 0.13° anchor disc (as in Experiment 4a) and a white 0.13° dot—with the eight possible initial positions of the white dot depicted in Fig. 4i. This ‘shapeless’ configuration in both corners was scaled to be equal to the larger circle from Experiment 3b. Both anchor discs were 13.40° from the nearest horizontal border of the display, and 8.90° from the nearest vertical border of the display. Observers simply reported whether the two white dots were in the same location relative to their respective central anchor discs. The magnitude of changes in the distance dimension was half that of the prior experiments, based on pilot data showing that observers were generally better at making these discriminations (perhaps because of the lack of a size translation).

Results

Matching accuracy is depicted in Fig. 4j and k, broken down as in Experiments 2b and 3b. Inspection of these results reveals a qualitative replication of the patterns observed in Experiment 3b: For angle changes, observers again performed better for dots near cardinal axes, relative to dots near oblique axes (12.7% [SD = 9.1%] vs. 34.1% [SD = 13.0%]), t(9) = 5.36, p < .001, d = 1.69—but again, no reliable difference was observed for distance changes (52.2% [SD = 24.5%] vs. 61.3% [SD = 17.7%]), t(9) = 1.43, p = .19, d = 0.45. Here, however, the interaction between these factors was marginal at best (in the same direction as in Experiment 3b, t(9) = 1.95, p = .08, d = 0.62.

Discussion

The current experiment again revealed spatial biases that were specific to both particular regions (cardinal vs. oblique) and particular dimensions (angle vs. distance changes)—though this latter contrast was weaker with this ‘shapeless’ configuration.

General discussion

The eight experiments reported here collectively reveal powerful, systematic angular biases in the representation of visual space: Observers consistently (mis-)localized objects as being closer to the centers of the quadrants to which they belonged, and consistently had poorer spatial resolution for angular information in these oblique regions of visual space.

Foundational biases?

These spatial biases seemed foundational in at least seven ways: First, they appeared in the context of maximally simple spatial tasks. The placement task (employed in Experiments 1, 2a, 3a, and 4a) merely required observers to reproduce a dot’s relative location, while the matching task (employed in Experiments 2b, 3b, 3c, and 4b) merely required observers to judge whether two dots were in the same relative locations. These tasks were designed precisely because they seemed like the simplest possible ways to assess the representation of spatial location. And critically, both tasks minimized memory demands as much as possible—because all of the relevant information in both tasks was simultaneously present on the display. This suggests that these biases reflect a primitive sort of spatial representation, rather than relying on more complex memory dynamics that may arise in tasks with sequentially presented stimuli. (If an observer had to indicate the location of a previously-viewed but now-disappeared object, then their performance could be readily influenced by many other factors—such as the statistics of where objects had previously appeared in that experiment, or by their prior probability distribution about where objects are likely to have appeared; cf. Howe & Purves, 2005. But in the present experiment the actual current location of the relevant object was always in plain sight during every phase of the trial—making it especially striking that the angular spatial biases were still observed.)

Second, and highly relatedly, these spatial biases did not seem to depend on either the presence or absence of the need for a size translation when equating relative locations. In the experiments with a square, circles, and triangles (Experiments 1–3), one of the two shapes was always much larger than the other (as is depicted in Fig. 1)—such that observers had to take this size difference into account in the matching task, and had to scale their response to the new size in the placement task. But in the experiments with the shapeless configuration (with only a central landmark; in Experiments 4a and 4b), there was no possibility for such a size translation in either task. The fact that the same qualitative patterns emerged in all these experiments suggests that the spatial biases do not in some way depend on the perhaps-subtle process of size translation.

Third, as is implicit in the points stressed above, these biases were not specific to any single experimental paradigm. Rather, the special role for oblique regions manifested in both the placement and matching tasks—making it unlikely that the results depended on any specific factor (such as the placement action itself), given how different these two tasks were.

Fourth, our stimuli themselves were also maximally simple. Plenty of research has used real-world objects in the context of spatial tasks involving pointing and reorientation (e.g., Simons & Wang, 1998), but, of course, such objects introduce complex shape and orientation cues that may themselves interact with spatial localization in intricate ways. In contrast, the ‘objects’ to be placed or matched in our tasks were always dots.

Fifth, many of these biases did not depend on the details of the bounding shapes. Whereas the quadrant-like biases for dots placed inside a square (as in Experiment 1) might simply reflect prioritization based on the particular angles and contours (or on the shape’s internal ‘skeleton’), it was especially striking that we observed these same biases even in both a circle (in Experiments 3a, 3b, and 3c) and in the shapeless configuration (in Experiments 4a and 4b). Critically, a circle does not have any prioritized regions based on angles or contours, and its medial-axis skeleton is just the central point. And, of course, the shapeless configuration lacked a bounding contour altogether. The fact that robust angular spatial biases still emerged with such (non-)shapes suggests that these effects pertain to the nature of spatial representation itself, rather than to shape-specific processing.

Sixth, the foundational nature of these angular biases is also suggested by the brute magnitudes of these effects. In the placement task, for example, the biases were readily apparent to the naked eye in both the figures of the final placement locations and in the corresponding online animations. In particular, the displacement from the cardinal regions of the square, circle, and shapeless configurations (as observed in Experiments 1, 3a, and 4a) is readily apparent even in the raw (i.e., unfiltered) placement results shown in Fig. 2b, h, and k—each of which depicts white horizontal and vertical ‘stripes’ of lower-density placements. Moreover, the magnitudes of these biases were also substantial, with dots frequently being misplaced by up to 20° in angular space (as is apparent from Fig. 3b, h, and k). And similarly, the magnitudes of the key differences in the matching task were also quite substantial—with the penalty in spatial resolution for angular changes in oblique regions (relative to cardinal regions) often cresting 20% (as is apparent by the differences between the red and blue lines for the nonzero angular differences in Fig. 4g and j).

Seventh, the spatial biases observed in this project were also remarkably consistent across observers. In the placement tasks that revealed quadrant-like structure (Experiments 1, 3a, and 4a), 29 of the 30 observers exhibited a bias towards the oblique regions of space. And in the relevant matching tasks (Experiments 3b, 3c and 4b), 27 of the 30 observers exhibited similar deficits in spatial resolution for angular differences in these oblique regions.

Limitations

Of course, there is one key way in which the quadrant-like angular biases discussed above did not seem so foundational: They did not always occur. In particular, they did not occur in either the placement or matching task when tested with a bounding triangle shape (in Experiments 2a and 2b). Instead, these experiments seemed to reveal related shape-specific effects. Dot placements in Experiment 2a seemed biased not toward the oblique regions (as was the case for the square, circle, and shapeless configuration) but rather toward the centers of each of the three medial axis branches (as illustrated in Fig. 2e and f)—and the corresponding matching results from Experiment 2b also revealed a systematic influence of ‘trirants’ rather than quadrants. And moreover, whereas the regions of greater placement density were always those same regions of lower spatial resolution for angular differences in the other shapes, for the triangle, the regions of greatest placement density had better spatial resolution for angular differences. This contrast is apparent from the fact that blue lines are below the red lines in Fig. 4g and j, but the blue line is above the red line in Fig. 4d.

At a minimum, this starkly different pattern of results with the triangular bounding shape reveals that the otherwise-uniform quadrant-like spatial bias is not universal. And as such, this indicates that these angular effects cannot be due to some primitive and inviolable feature of the underlying cognitive or neural architecture. Rather, the quadrant-like effects seem to operate when shapes are not so salient or structured (as with the circle or shapeless configuration in Experiments 3a, 3b, 3c, 4a, and 4b), and/or when those shapes themselves have a quadrant-like structure (as with the square in Experiment 1). Our primary focus in the present paper has been on the implications for spatial representation, but, naturally, this nonuniversality calls for testing a wider variety of shapes with both of these paradigms in future work (cf. Langlois et al., 2017).

The current experiments also had several other limitations that should be addressed in future work. Perhaps most salient is the fact that because we did not monitor eye movements or head movements, we cannot know the type of reference frame in which the key angular biases operate. It could be, for example, that observers tended to fixate the centroids of the shapes (or the central anchor point[s] in Experiments 4a and 4b) when making their responses, such that the biases operate in retinal coordinates—showing a displacement toward retinally oblique regions of space in the placement task, and lower spatial resolution for retinally oblique regions of space in the matching task. Or it could be that these same biases would appear regardless of where observers were fixating (or, say, even if they fixated in the center of the display as a whole)—as would be expected if these biases operate in object-centered rather than retinal coordinates. And, of course, these possibilities are not mutually exclusive. Work on spatial disorders such as neglect has revealed that some patients neglect the left side of retinal visual space as a whole, while others neglect the left side of each individual object, while still others neglect the left side of each object’s canonical orientation, even if it appears in a noncanonical orientation (e.g., Subbiah & Caramazza, 2000). Future work could answer such questions by repeating these experiments while monitoring or controlling fixations.

In Experiments 3 and 4, we observed systematic spatial distortions even for configurations (Circle and Shapeless, respectively) that have no intrinsic spatial axes. Why? One possibility is that there is a tendency to subdivide (otherwise undifferentiated) space into quadrants based on some extrinsic identifiable reference frame—such as the rectangular computer screen itself, the observers’ own bilaterally symmetric bodies, or even the surrounding rectilinear testing room. We know from prior work that various other perceptual and cognitive effects can be based on reference frames that are viewer centered, object centered, or even environment centered (Farah, Brunn, Wong, Wallace, & Carpenter, 1990). And observers famously fail to represent an object’s orientation that is independent from its local environment (Witkin & Asch, 1948). Therefore, it would be reasonable to assume that the ‘default’ subdivisions revealed here reflect a reference frame imputed from the orientation of the screen and/or the surrounding room. This could be tested in future work by exploring whether similar spatial biases exist when observers view the displays through a circular aperture (or even when the stimuli are projected inside a ganzfeld so that there is no visible reference frame at all). Note, however, that the present work is less about the exact quadrant-like orientation of these subdivisions and more about the fact that they exist in the first place in our tasks— a result that was certainly not entailed by previous work on reference frames.

Finally, it is also worth stressing two additional limitations of the final two experiments that used the ‘shapeless’ configuration (Experiments 4a and 4b). In some ways, the results of these two experiments were the most surprising—because they indicated that the angular spatial biases operated even without any bounding shape contours at all, and without any size translation. However, it was still the case in the placement task (in Experiment 4a) that the underlying distribution of initial dot locations had a circular structure (as is apparent in Fig. 2j). And, similarly, the baseline dot locations tested in the matching task (in Experiment 4b) still also had a circular configuration (as is apparent in Fig. 4i). As such, it is possible that observers may have implicitly learned this circular structure as the trials progressed, and that it is this implicit shape that that somehow led to our results (even though a circle still does not prioritize any particular regions given its lack of separate angles or contours). So, it would be interesting to repeat these experiments with different underlying initial dot distributions. (And it might be especially interesting to see if a quadrant-like pattern of results still emerges even if the initial distribution of dots has a triangular shape.) In addition, we feel a need to stress again that the matching results with the shapeless configuration were notably weaker than with the bounding shapes. In particular, the key interaction between angular/distance information and oblique/cardinal regions that was so reliable for the circle (in Experiment 3b) was only marginal at best in this study, even though it was in the same direction. So, whereas our sample size (of 10 observers per experiment) seemed sufficient to capture the patterns in each other experiments (including the analogous shape-specific effects with the Triangle in Experiment 2b), future matching experiments with the shapeless configuration would benefit from a greater sample size.

Relation to prior work

Our primary aim in this project is to report hopefully provocative new data, rather than to offer a theoretical account or model for these effects. But it does seem necessary to explore whether and how past models and other effects might (or might not) be able to explain these data. That is the burden of this section (and also the sections titled “Do We Represent Space in Polar Coordinates?”).

Prototype effects and the ‘category adjustment model’

On the surface, the angular spatial biases observed in this study most closely resemble so-called prototype effects in spatial memory. When observers must reproduce a dot location from memory, for example, similar patterns of biases are observed (e.g., Huttenlocher et al., 1991; Huttenlocher et al., 2000). In particular, the ‘sawtooth’ patterns for angular errors that resulted from the matching experiments—as observed in Fig. 3b, e, h, and k—very clearly resemble the patterns depicted in Figs. 3, 6, and 8 of Huttenlocher et al. (1991).

However, the current experiments go beyond these original studies in several related respects. Empirically, it remains possible that the biases observed in this earlier work pertained not to spatial representation per se, but rather to memory dynamics. Critically, all of these experiments of which we are aware asked observers to indicate a location after the relevant information had disappeared from the display—whereas in the current experiments all of the relevant information was always fully visible. As such, none of these earlier studies necessitated the present results: It would be entirely consistent with this past work for such biases to have disappeared fully when memory demands are eliminated or minimized—and it seems plausible that other factors (such as Bayesian priors for where objects were likely to have appeared) would play a much more prominent role when the relevant information is not currently staring observers in the face. In addition, all of this earlier work to our knowledge used bounding shapes (and, indeed, much of the follow-up work has focused primarily on shape-based effects; e.g., Langlois et al., 2017; Wedell et al., 2007), such that these results might plausibly all be shape-specific phenomena that depend on the existence of these contours. In contrast, the current project revealed clear angular biases even without any bounding shapes at all (robustly in Experiment 4a, and to a weaker extent in Experiment 4b).

Relatedly, a ‘weighted-distortion theory’ has been proposed based on this sort of work, and it attempts to explain radial placement biases via three postulates: (1) boundaries serve as landmarks, (2) there is a bias towards landmarks, and (3) the magnitude of the bias increases with distance from the landmarks (Nelson & Chaiklin, 1980). Note, however, that this theory is based only on placement within a single dimension, and thus it fails to account for the most salient aspect of the spatial distortions observed in both our work and in prior work (viz. the angular distortions; Huttenlocher et al., 1991). That said, our experiments do provide evidence to support at least the third postulate: Errors were greater for points originally farther away from the oblique axes. Perhaps, on this view, the ‘prototype’ locations (like the boundaries) act as landmarks (thereby also providing support for Postulate #2).

Perhaps the biggest contrast with this earlier work, however, is theoretical. Prototype effects have been explained primarily by appeal to higher-level categories (and indeed this work is often referred to in terms of the ‘category adjustment model’). And, in some cases, these categories can be quite high-level—for example, showing that spatial memory for an object in a shape depends on whether it is described as a dot in a polygon, or as a city in a region (e.g., Friedman, Montello, & Burte, 2012). In contrast, we have stressed how these results may reflect relatively low-level aspects of spatial representation that do not depend on memory, that do not require bounding shapes (recognizable or otherwise), and that may reflect aspects of low-level visual processing rather than higher-level categorization (cf. Firestone & Scholl, 2016).

Serial reproduction

The spatial biases we observed also strongly resemble those from a recent study of serial reproduction (Langlois et al., 2017). Each individual step of these experiments is similar to the prototype-effect studies: Observers view a dot placed inside a bounding shape, and then after the dot disappears, they must reproduce its location. Critically, however, the position chosen by a given observer then serves as the input location for the next observer—and of interest are how the resulting placement patterns change and converge over time. The resulting patterns of convergence (for shapes such as a circle, triangle, and square) each strongly resembled the placement results observed in the current project (and these researchers also tested several other shapes as well). For example, the quadrant-like structure observed in Fig. 2c and i looks qualitatively similar to that in Figures 3 and 5 from Langlois et al. (2017)—and this was also true for the ‘trirant’-like structure we observed with our triangle shape (compare our Fig. 2f and their Fig. 4).

In future work, it would be interesting to explore such connections—and it certainly seems promising to find such similarities across such different types of paradigms. However, this serial reproduction work also seems different in several respects, both empirically and theoretically. Empirically, it seems worth noting that despite the qualitative similarities noted above, there were also several types of more nuanced differences in the patterns of serial convergence in this other work, compared with our observed placement biases. To take one example, the higher-density regions in our placement data, with both the square and the triangle, were each relatively undifferentiated ‘clumps’, as is clear from Fig. 2c and f. But in this serial reproduction work, each of these clumps had a clearly defined inverted-V pattern, as depicted in their Fig. 5b. This can also be described as a clear exodus away from certain parts of the medial-axis branches, which we never observed. We can speculate that this subtle difference may reflect differences in how ‘intentional’ the placements were in our two tasks—because our task required relatively quick responding, whereas the serial reproduction work allowed unlimited time for responses—but future work will be necessary to clarify this. Theoretically, this serial reproduction work—like the earlier work on the ‘prototype effect’—has also placed a great emphasis on shape representation per se, and all of these experiments involved bounding shapes. In contrast, our key patterns also replicated in Experiment 4a (and to a lesser extent in Experiment 4b) using a shapeless configuration, and so we have stressed how such results may reflect aspects of spatial representation per se. And of course, this suggests that it could be especially interesting to repeat the studies of Langlois et al. (2017) without using any bounding contours at all.

The oblique effect

The matching results in our studies indicated worse performance for discriminating angular differences in oblique regions (in Experiments 3b, 3c, and 4b), and this seems reminiscent of the ‘oblique effect’—in which observers perform worse in many contexts at discriminating diagonal lines compared with horizontal and vertical lines (e.g., Appelle, 1972; Keil & Cristóbal, 2000; see also Greene, 1993; Greene, Frawley, & Swimm, 2000, for other examples of spatial distortions within oblique regions). The oblique effect is powerful enough in some contexts to work as a classroom demonstration—for example, people are much better at telling if a hung painting is offset from being purely vertical or horizontal, compared with telling if it is offset from being hung at 45°. In both cases, we see a deficit for processing information in oblique configurations.

However, the current work also contrasts with the oblique effect in important ways, both empirically and theoretically. Empirically, the biggest difference is that work on the oblique effect nearly always involves oriented stimuli—whereas the key stimuli in the present experiments were (orientation-less) dots. As such, it would have been fully consistent with the existing work on the oblique effect to find no such effects (or even opposite effects) in the present experiments.

Theoretically, the oblique effect is often explained by appeal to relatively low-level factors of neural representation—including the observation that more neurons in early visual areas such as V1 are tuned to cardinal orientations (e.g., Furmanski & Engel, 2000; Li, Peterson, & Freeman, 2003). But the current results cannot be explained by appeal to any such unchanging features of the underlying neural architecture, because they depended critically on the bounding shape being tested. The oblique effect may operate in all contexts because every possible stimulus is represented using the same distribution of orientation-selective cells in V1, which are so nonuniformly distributed. But in our experiments, the quadrant-like structure disappeared when testing the triangle—in which some of the diagonal regions (corresponding to the triangle’s medial-axis branches) featured the best matching performance for angular information (in Experiment 2b). Thus, these two classes of phenomena may be implemented at different levels of processing.

Do we represent space in polar coordinates?

Might the results from this project shed light on the underlying ‘format’ of our cognitive maps? Recent work (Yang & Flombaum, 2018) has raised the possibility that space is fundamentally represented in the mind in polar coordinates (i.e., in terms of angle/distance relationships) rather than in the perhaps-more-intuitive Cartesian coordinate system (i.e., in terms of distance along orthogonal x and y dimensions). This recent work showed that errors in simple localization tasks were better explained by appeal to a polar format, and also that overlapping contours of various types could be recognized more readily when they involved circular/radial patterns compared with rectilinear patterns.

The current experiments are generally consistent with this perspective—especially insofar as we observed some differences between angular and distance information in the matching experiments (as depicted in Fig. 4)—and this suggests that the current paradigms might also prove useful in future work for testing hypotheses about polar versus Cartesian coordinate frames. This possible connection must remain speculative for now, though, for at least two reasons. First, the polar contrast was, of course, built into the design of our matching experiments themselves, because they featured offsets only along the angular and distance dimensions. It thus remains to be seen whether these same dimensions would best capture performance if the offsets were instead more random (or if they were aligned only along orthogonal Cartesian directions). Second, we did not observe a full double-dissociation for angle and distance: Although performance systematically differed for dots originating in oblique versus cardinal regions in the context of angular offsets (as in Fig. 4g and j), this was not true for distance offsets (as in Fig. 4h and k).

Conclusion

Intuitively (and almost by definition), space seems isotropic. But the fundamental lesson of this project is that not all spatial regions or dimensions are created equal. At a relatively fundamental level in visual processing—and as revealed in exceptionally simple spatial tasks—the resolution of spatial representation may differ for different regions and dimensions of space itself.

Author note

For helpful conversation and/or comments on previous drafts, we thank Talia Konkle, Nora Newcombe, and the members of the Yale Cognition and Development Laboratory and the Yale Perception and Cognition Laboratory. This project was funded by ONR MURI #N00014-16-1-2007 awarded to B.J.S. and by an NSF Graduate Research Fellowship awarded to S.R.Y.

Preregistrations and raw data for each experiment can be accessed at https://osf.io/7asuw/.