Contact Time of Double-Droplet Impacting Superhydrophobic Surfaces with Different Macrotextures
Abstract
:1. Introduction
2. Mathematical Model
2.1. Shan-Chen Lattice Boltzmann Model
2.2. Model Validation
2.3. Simulation Setup
3. Results and Discussion
3.1. Double-Droplet Impact Dynamics
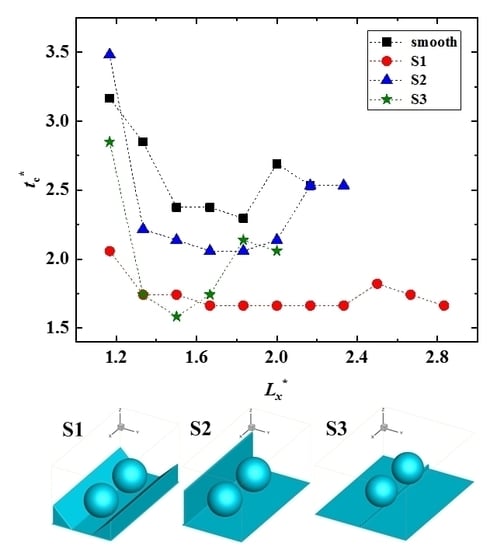
3.2. Contact Time on the S1 Surface
3.3. Contact Time on the S2 Surface
3.4. Contact Time on the S3 Surface
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Richard, D.; Clanet, C.; Quéré, D. Surface phenomena: Contact time of a bouncing drop. Nature 2002, 417, 811. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.-J.; Zhang, L.-Z.; Yi, M.-C.; Wang, X.; Gao, S.-R.; Yang, Y.-R.; Wang, X.-D. Rebound Dynamics of Two Droplets Successively Impacting an Inclined Surface. Coatings 2020, 10, 592. [Google Scholar] [CrossRef]
- Tembely, M.; Vadillo, D.; Soucemarianadin, A.; Dolatabadi, A. Numerical Simulations of Polymer Solution Droplet Impact on Surfaces of Different Wettabilities. Processes 2019, 7, 798. [Google Scholar] [CrossRef] [Green Version]
- Xie, F.-F.; Lv, S.-H.; Yang, Y.-R.; Wang, X.-D. Contact Time of a Bouncing Nanodroplet. J. Phys. Chem. Lett. 2020, 11, 2818–2823. [Google Scholar] [CrossRef]
- Zhang, Z.; Ge, B.; Men, X.; Li, Y. Mechanically durable, superhydrophobic coatings prepared by dual-layer method for anti-corrosion and self-cleaning. Colloids Surf. A Physicochem. Eng. Asp. 2016, 490, 182–188. [Google Scholar] [CrossRef]
- Shen, Y.; Tao, H.; Chen, S.-L.; Xie, Y.; Zhou, T.; Wang, T.; Tao, J. Water repellency of hierarchical superhydrophobic Ti6Al4V surfaces improved by secondary nanostructures. Appl. Surf. Sci. 2014, 321, 469–474. [Google Scholar] [CrossRef]
- Tsai, P.A.; Pacheco, S.; Pirat, C.; Lefferts, L.; Lohse, D. Drop Impact upon Micro- and Nanostructured Superhydrophobic Surfaces. Langmuir 2009, 25, 12293–12298. [Google Scholar] [CrossRef] [Green Version]
- Lv, C.; Hao, P.; Zhang, X.; He, F. Drop impact upon superhydrophobic surfaces with regular and hierarchical roughness. Appl. Phys. Lett. 2016, 108, 141602. [Google Scholar] [CrossRef]
- Bird, J.C.; Dhiman, R.; Kwon, H.-M.; Varanasi, K.K. Reducing the contact time of a bouncing drop. Nature 2013, 503, 385–388. [Google Scholar] [CrossRef]
- Gauthier, A.; Symon, S.; Clanet, C.; Quéré, D. Water impacting on superhydrophobic macrotextures. Nat. Commun. 2015, 6, 8001. [Google Scholar] [CrossRef]
- Shen, Y.; Tao, J.; Tao, H.; Chen, S.; Pan, L.; Wang, T. Approaching the theoretical contact time of a bouncing droplet on the rational macrostructured superhydrophobic surfaces. Appl. Phys. Lett. 2015, 107, 111604. [Google Scholar] [CrossRef]
- Lin, D.-J.; Wang, L.; Wang, X.-D.; Yan, W.-M. Reduction in the contact time of impacting droplets by decorating a rectangular ridge on superhydrophobic surfaces. Int. J. Heat Mass Transf. 2019, 132, 1105–1115. [Google Scholar] [CrossRef]
- Liu, Y.; Andrew, M.; Li, J.; Yeomans, J.M.; Wang, Z. Symmetry breaking in drop bouncing on curved surfaces. Nat. Commun. 2015, 6, 10034. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, S.; Zhu, C.; Tao, J.; Chen, Z.; Tao, H.; Pan, L.; Wang, G.; Wang, T. Bouncing dynamics of impact droplets on the convex superhydrophobic surfaces. Appl. Phys. Lett. 2017, 110, 221601. [Google Scholar] [CrossRef]
- Chantelot, P.; Moqaddam, A.M.; Gauthier, A.; Chikatamarla, S.S.; Clanet, C.; Karlin, I.V.; Quéré, D. Water ring-bouncing on repellent singularities. Soft Matter 2018, 14, 2227–2233. [Google Scholar] [CrossRef] [PubMed]
- Regulagadda, K.; Bakshi, S.; Das, S.K. Triggering of flow asymmetry by anisotropic deflection of lamella during the impact of a drop onto superhydrophobic surfaces. Phys. Fluids 2018, 30, 072105. [Google Scholar] [CrossRef]
- Zhou, W. Lattice Boltzmann simulation of coalescence of multiple droplets on nonideal surfaces. Phys. Rev. E 2015, 92, 053307. [Google Scholar] [CrossRef]
- Raman, K.A.; Jaiman, R.K.; Lee, T.-S.; Low, H.-T. Dynamics of simultaneously impinging drops on a dry surface: Role of impact velocity and air inertia. J. Colloid Interface Sci. 2017, 486, 265–276. [Google Scholar] [CrossRef]
- Qian, J.; Law, C.K. Regimes of coalescence and separation in droplet collision. J. Fluid Mech. 1997, 331, 59–80. [Google Scholar] [CrossRef]
- Amani, A.; Balcázar, N.; Gutiérrez, E.; Oliva, A. Numerical study of binary droplets collision in the main collision regimes. Chem. Eng. J. 2019, 370, 477–498. [Google Scholar] [CrossRef]
- Yuan, Z.; Hu, Z.; Chu, F.; Wu, X. Enhanced and guided self-propelled jumping on the superhydrophobic surfaces with macrotexture. Appl. Phys. Lett. 2019, 115, 163701. [Google Scholar] [CrossRef]
- Lu, D.; Zhao, M.; Zhang, H.; Yang, Y.; Zheng, Y. Self-Enhancement of Coalescence-Induced Droplet Jumping on Superhydrophobic Surfaces with an Asymmetric V-Groove. Langmuir 2020, 36, 5444–5453. [Google Scholar] [CrossRef]
- Wang, X.; Lin, D.-J.; Wang, Y.-B.; Gao, S.-R.; Yang, Y.-R.; Wang, X.-D. Rebound dynamics of two droplets simultaneously impacting a flat superhydrophobic surface. AIChE J. 2020, e16647. [Google Scholar] [CrossRef]
- Zheng, S.; Eimann, F.; Philipp, C.; Fieback, T.; Gross, U. Single droplet condensation in presence of non-condensable gas by a multi-component multi-phase thermal lattice Boltzmann model. Int. J. Heat Mass Transf. 2019, 139, 254–268. [Google Scholar] [CrossRef]
- Zheng, S.; Eimann, F.; Fieback, T.; Xie, G.; Gross, U. Numerical investigation of convective dropwise condensation flow by a hybrid thermal lattice Boltzmann method. Appl. Therm. Eng. 2018, 145, 590–602. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Li, X.J. Lattice Boltzmann modeling of multiphase flows at large density ratio with an improved pseudopotential model. Phys. Rev. E 2013, 87, 053301. [Google Scholar] [CrossRef] [Green Version]
- Yuan, P.; Schaefer, L. Equations of state in a lattice Boltzmann model. Phys. Fluids 2006, 18, 42101. [Google Scholar] [CrossRef]
- Zhang, D.; Papadikis, K.; Gu, S. Three-dimensional multi-relaxation time lattice-Boltzmann model for the drop impact on a dry surface at large density ratio. Int. J. Multiph. Flow 2014, 64, 11–18. [Google Scholar] [CrossRef]
- Zhang, D.; Papadikis, K.; Gu, S. Application of a high density ratio lattice-Boltzmann model for the droplet impingement on flat and spherical surfaces. Int. J. Therm. Sci. 2014, 84, 75–85. [Google Scholar] [CrossRef]
- Shi, Y.; Tang, G.; Xia, H. Investigation of coalescence-induced droplet jumping on superhydrophobic surfaces and liquid condensate adhesion on slit and plain fins. Int. J. Heat Mass Transf. 2015, 88, 445–455. [Google Scholar] [CrossRef]
- Lin, D.J.; Zhang, L.Z.; Yi, M.C.; Gao, S.R.; Yang, Y.R.; Wang, X.D. Contact time on inclined superhydrophobic surfaces decorated with parallel macro-ridges. Colloids Surf. A Physicochem. Eng. Asp. 2020, 599, 124924. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Q.; Zhou, C.Q.; Zhou, P.; Yan, H. Investigation of droplet evaporation on heterogeneous surfaces using a three-dimensional thermal multiphase lattice Boltzmann model. Appl. Therm. Eng. 2017, 127, 1346–1354. [Google Scholar] [CrossRef]
- Zhang, L.-Z.; Yuan, W.-Z. A lattice Boltzmann simulation of coalescence-induced droplet jumping on superhydrophobic surfaces with randomly distributed structures. Appl. Surf. Sci. 2018, 436, 172–182. [Google Scholar] [CrossRef]
- Clanet, C.; Béguin, C.; Richard, D.; Quéré, D. Maximal deformation of an impacting drop. J. Fluid Mech. 2004, 517, 199–208. [Google Scholar] [CrossRef]
- Farhangi, M.M.; Graham, P.J.; Choudhury, N.R.; Dolatabadi, A. Induced Detachment of Coalescing Droplets on Superhydrophobic Surfaces. Langmuir 2012, 28, 1290–1303. [Google Scholar] [CrossRef] [PubMed]

















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.-J.; Zhang, L.-Z.; Yi, M.-C.; Wang, X.; Gao, S.-R.; Yang, Y.-R.; Zheng, S.-F.; Wang, X.-D. Contact Time of Double-Droplet Impacting Superhydrophobic Surfaces with Different Macrotextures. Processes 2020, 8, 896. https://doi.org/10.3390/pr8080896
Lin D-J, Zhang L-Z, Yi M-C, Wang X, Gao S-R, Yang Y-R, Zheng S-F, Wang X-D. Contact Time of Double-Droplet Impacting Superhydrophobic Surfaces with Different Macrotextures. Processes. 2020; 8(8):896. https://doi.org/10.3390/pr8080896
Chicago/Turabian StyleLin, Dian-Ji, Ling-Zhe Zhang, Meng-Chao Yi, Xin Wang, Shu-Rong Gao, Yan-Ru Yang, Shao-Fei Zheng, and Xiao-Dong Wang. 2020. "Contact Time of Double-Droplet Impacting Superhydrophobic Surfaces with Different Macrotextures" Processes 8, no. 8: 896. https://doi.org/10.3390/pr8080896