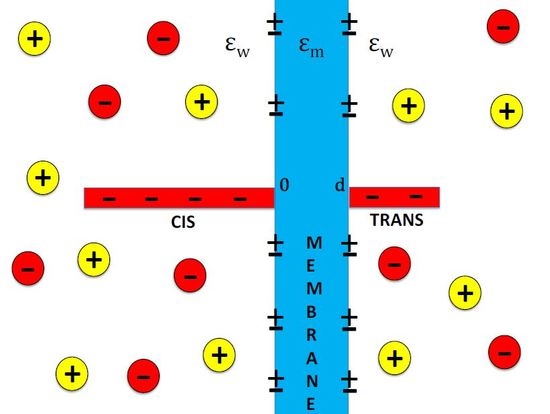
Dielectric Trapping of Biopolymers Translocating through Insulating Membranes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Charge Composition of the System
2.2. Modified Fokker–Planck Equation
2.3. Capture Velocity and Translocation Time
2.4. Electrostatic Polymer Potential
3. Results and Discussion
3.1. Drift-Driven Regime
3.2. Neutral Membranes: Dielectric Trapping
3.2.1. Dielectric Trapping of the Polymer in Dilute Salt
3.2.2. Effect of Polymer Length and Finite Salt Concentration
3.3. Charged Membranes
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A. Variational Evaluation of the Dressed Polymer Charge
Appendix B. Derivation of the FP Equation (6)
Appendix C. Calculation of the Translocation Time
Appendix D. Derivation of the Polymer Interaction Potential ΔΩp(s)
Appendix D.1. Polymer–Membrane Coupling Energy Ωpm(s)
Appendix D.2. Polymer Self-Energy ΔΩs(s) and Total Electrostatic Polymer Potential ΔΩp(s)
References
- Kasianowicz, J.J.; Brandin, E.; Branton, D.; Deamer, D.W. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. USA 1996, 93, 13770–13773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henrickson, S.E.; Misakian, M.; Robertson, B.; Kasianowicz, J.J. Driven DNA transport into an asymmetric nanometer-scale pore. Phys. Rev. Lett. 2000, 14, 3057–3060. [Google Scholar] [CrossRef] [PubMed]
- Meller, A.; Nivon, L.; Branton, D. Voltage-Driven DNA Translocations through a Nanopore. Phys. Rev. Lett. 2001, 86, 3435–3438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonthuis, D.J.; Zhang, J.; Hornblower, B.; Mathé, J.; Shklovskii, B.I.; Meller, A. Self-Energy-Limited Ion Transport in Subnanometer Channels. Phys. Rev. Lett. 2006, 97, 128104. [Google Scholar] [CrossRef] [PubMed]
- Smeets, R.M.M.; Keyser, U.F.; Krapf, D.; Wue, M.-Y.; Dekker, N.H.; Dekker, C. Salt dependence of ion transport and DNA translocation through solid-state nanopores. Nano Lett. 2006, 6, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Clarke, J.; Wu, H.C.; Jayasinghe, L.; Patel, A.; Reid, S.; Bayley, H. Continuous base identification for single-molecule nanopore DNA sequencing. Nat. Nanotechnol. 2009, 4, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Wanunu, M.; Morrison, W.; Rabin, Y.; Grosberg, A.Y.; Meller, A. Electrostatic focusing of unlabelled DNA into nanoscale pores using a salt gradient. Nat. Nanotechnol. 2010, 5, 160–165. [Google Scholar] [CrossRef] [PubMed]
- Sung, W.; Park, P.J. Polymer Translocation through a Pore in a Membrane. Phys. Rev. Lett. 1996, 77, 783. [Google Scholar] [CrossRef] [PubMed]
- Luo, K.; Huopaniemi, I.; Ala-Nissila, T.; Ying, S.C. Polymer translocation through a nanopore under an applied external field. J. Chem. Phys. 2006, 124, 114704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakaue, T. Nonequilibrium dynamics of polymer translocation and straightening. Phys. Rev. E 2007, 76, 021803. [Google Scholar] [CrossRef] [PubMed]
- Ikonen, T.; Bhattacharya, A.; Ala-Nissila, T.; Sung, W. Unifying model of driven polymer translocation. Phys. Rev. E 2012, 85, 051803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farahpour, F.; Maleknejad, A.; Varnikc, F.; Ejtehadi, M.R. Chain deformation in translocation phenomena. Soft Matter 2013, 9, 2750–2759. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Ala-Nissila, T.; Metzler, R. Polymer translocation: The first two decades and the recent diversification. Soft Matter 2014, 10, 9016–9037. [Google Scholar] [CrossRef] [PubMed]
- Sarabadani, J.; Ala-Nissila, T. Theory of pore-driven and end-pulled polymer translocation dynamics through a nanopore: An overview. J. Phys. Condens. Matter 2018, 30, 274002. [Google Scholar] [CrossRef] [PubMed]
- Ghosal, S. Effect of Salt Concentration on the Electrophoretic Speed of a Polyelectrolyte through a Nanopore. Phys. Rev. Lett. 2007, 98, 238104. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Shklovskii, B.I. Effective charge and free energy of DNA inside an ion channel. Phys. Rev. E 2007, 75, 021906. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.T.A.; Muhtukumar, M. Polymer translocation through alpha-hemolysin pore with tunable polymer-pore electrostatic interaction. J. Chem. Phys. 2010, 133, 045101. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Rabin, Y. DNA capture into a nanopore: Interplay of diffusion and electrohydrodynamics. J. Chem. Phys. 2010, 133, 165102. [Google Scholar] [CrossRef] [PubMed]
- Buyukdagli, S.; Ala-Nissila, T.; Blossey, R. Ionic current inversion in pressure-driven polymer translocation through nanopores. Phys. Rev. Lett. 2015, 114, 088303. [Google Scholar] [CrossRef] [PubMed]
- Buyukdagli, S.; Ala-Nissila, T. Controlling Polymer Capture and Translocation by Electrostatic Polymer-pore interactions. J. Chem. Phys. 2017, 147, 114904. [Google Scholar] [CrossRef] [PubMed]
- Buyukdagli, S. Facilitated polymer capture by charge inverted electroosmotic flow in voltage-driven polymer translocation. Soft Matter 2018, 14, 3541–3549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buyukdagli, S.; Ala-Nissila, T. Electrostatics of polymer translocation events in electrolyte solutions. J. Chem. Phys. 2016, 145, 014902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Netz, R.R.; Orland, H. Variational charge renormalization in charged systems. Eur. Phys. J. E Soft Matter 2003, 11, 301–311. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Avalos, J.B.; Rubi, J.M.; Bedeaux, D. Dynamics of rodlike polymers in dilute solution. Macromolecules 1993, 26, 2550–2561. [Google Scholar] [CrossRef]
- Firnkes, M.; Pedone, D.; Knezevic, J.; Döblinger, M.; Rant, U. Electrically facilitated translocations of proteins through silicon nitride nanopores: Conjoint and competitive action of diffusion, electrophoresis, and electroosmosis. Nano Lett. 2010, 10, 2162–2167. [Google Scholar] [CrossRef] [PubMed]
- Meller, A.; Branton, D. Single molecule measurements of DNA transport through a nanopore. Electrophoresis 2002, 23, 2583–2591. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Siegman, A.E. Simplified derivation of the Fokker-Planck equation. Am. J. Phys. 1979, 47, 545–547. [Google Scholar] [CrossRef]
- Ansalone, M.; Chinappi, L.; Rondoni, L.; Cecconi, F. Driven diffusion against electrostatic or effective energy barrier across α-hemolysin. J. Chem. Phys. 2015, 143, 154109. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buyukdagli, S.; Sarabadani, J.; Ala-Nissila, T. Dielectric Trapping of Biopolymers Translocating through Insulating Membranes. Polymers 2018, 10, 1242. https://doi.org/10.3390/polym10111242
Buyukdagli S, Sarabadani J, Ala-Nissila T. Dielectric Trapping of Biopolymers Translocating through Insulating Membranes. Polymers. 2018; 10(11):1242. https://doi.org/10.3390/polym10111242
Chicago/Turabian StyleBuyukdagli, Sahin, Jalal Sarabadani, and Tapio Ala-Nissila. 2018. "Dielectric Trapping of Biopolymers Translocating through Insulating Membranes" Polymers 10, no. 11: 1242. https://doi.org/10.3390/polym10111242