Monitored Tomographic Reconstruction—An Advanced Tool to Study the 3D Morphology of Nanomaterials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis and Characterization of the MoNi4/MoO2@Ni Material System
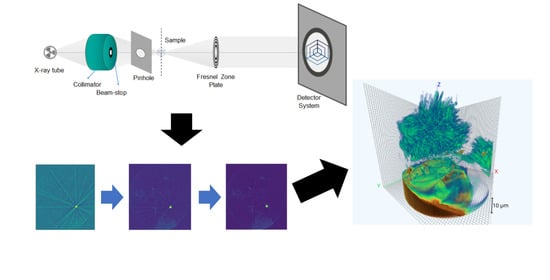
2.2. Nano-XCT (Laboratory Tool)
3. Monitored Reconstruction
3.1. Cost of the Collected Projections
3.2. Absolute and Relative Estimation Errors
3.3. Stopping Rules
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zschech, E.; Löffler, M.; Krüger, P.; Gluch, J.; Kutukova, K.; Zglobicki, I.; Silomon, J.; Rosenkranz, R.; Standke, Y.; Topal, E. Laboratory Computed X-ray Tomography–A Nondestructive Technique for 3D Microstructure Analysis of Materials. Pract. Metallogr. 2018, 55, 539–555. [Google Scholar] [CrossRef]
- Jacobsen, C. X-ray Microscopy. In Contemporary Physics; Cambridge University Press: Cambridge, UK, 2020; Volume 61, pp. 147–148. [Google Scholar]
- Ourselin, S.; Joskowicz, L.; Sabuncu, M.R.; Unal, G.; Wells, W. (Eds.) Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016; Springer International Publishing: New York, NY, USA, 2016; pp. 432–440. [Google Scholar]
- Zhang, H.; Li, L.; Qiao, K.; Wang, L.; Yan, B.; Li, L.; Hu, G. Image Prediction for Limited-angle Tomography via Deep Learning with Convolutional Neural Network. Medical Physics (physics.med-ph); Computer Vision and Pattern Recognition (cs.CV), Submitted on 29 July 2016. Available online: https://arxiv.org/abs/1607.08707 (accessed on 12 July 2021).
- Yang, X.; De Andrade, V.; Scullin, W.; Dyer, E.L.; Kasthuri, N.; De Carlo, F.; Gürsoy, D. Low-dose x-ray tomography through a deep convolutional neural network. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.; Zhang, Y.; Zhang, W.; Liao, P.; Li, K.; Zhou, J.; Wang, G. Low-dose CT via convolutional neural network. Biomed. Opt. Express 2017, 8, 679–694. [Google Scholar] [CrossRef] [PubMed]
- Topal, E.; Löffler, M.; Zschech, E. Deep Learning-based Inaccuracy Compensation in Reconstruction of High Resolution XCT Data. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Topal, E.; Liao, Z.; Löffler, M.; Gluch, J.; Zhang, J.; Feng, X.; Zschech, E. Multi-scale X-ray tomography and machine learning algorithms to study MoNi4 electrocatalysts anchored on MoO2 cuboids aligned on Ni foam. BMC Mater. 2020, 2, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Topal, E.; Rajendran, H.; Zgłobicka, I.; Gluch, J.; Liao, Z.; Clausner, A.; Kurzydłowski, K.J.; Zschech, E. Numerical and Ex-perimental Study of the Mechanical Response of Diatom Frustules. J. Nanomater. 2020, 10, 959. [Google Scholar] [CrossRef] [PubMed]
- Bulatov, K.; Chukalina, M.; Buzmakov, A.; Nikolaev, D.; Arlazarov, V.V. Monitored Reconstruction: Computed Tomography as an Anytime Algorithm. IEEE Access 2020, 8, 110759–110774. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, T.; Liu, P.; Liao, Z.; Liu, S.; Zhuang, X.; Chen, M.; Zschech, E.; Feng, X. Efficient hydrogen production on MoNi4 electrocatalysts with fast water dissociation kinetics. Nat. Commun. 2017, 8, 15437. [Google Scholar] [CrossRef] [PubMed]
- Description of the Smart Tomo Engine Software. Available online: https://smartengines.com/ocr-engines/tomo-engine/ (accessed on 12 July 2021).
- Yamaev, A.; Chukalina, M.; Nikolaev, D.; Sheshkus, A.; Chulichkov, A. Lightweight denoising filtering neural network for FBP algorithm. Proc. SPIE 2021, 11605, 116050L. [Google Scholar] [CrossRef]
- Smelkina, N.A.; Kolsanov, A.V.; Chaplygin, S.S.; Zelter, P.; Khramov, A.G. Pulmonary Emphysema Recognition by CT scan. Comput. Opt. 2017, 41, 726–731. [Google Scholar] [CrossRef]
- Guan, H.; Gordon, R. Computed tomography using algebraic reconstruction techniques (ARTs) with different projection access schemes: A comparison study under practical situations. Phys. Med. Biol. 1996, 41, 1727. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, T. Mathematical Statistics: A Decision Theoretic Approach, Ser. Probability and Mathematical Statistics; Academic Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Bulatov, K.; Mukovozov, A.; Arlazarov, V.V. Empirical analysis of the optimality of RSRE-based stopping rules for monitored reconstruction. Proc. SPIE 2021, 11605, 116051Y. [Google Scholar] [CrossRef]
- Ferguson, T. Optimal Stopping and Applications. Available online: https://www.math.ucla.edu/~tom/Stopping/Contents.html (accessed on 12 July 2021).
- Berezovskij, B.A.; Gnedin, A.B. Theory of choice and the problem of optimal stopping at the best entity. Autom. Remote Control 1981, 42, 1221–1225. [Google Scholar]
- Chow, Y.S.; Robbins, H. A Martingale System Theorem and Applications. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability Berkeley; University of California Press: Berkley, CA, USA, 1961; Volume 1, pp. 93–104. [Google Scholar]
- Zilberstein, S. Using anytime algorithms in intelligent systems. AI Mag. 1996, 17, 73–83. [Google Scholar]
- Bulatov, K.; Chukalina, M.; Nikolaev, D. Fast X-Ray Sum Calculation Algorithm for Computed Tomography Problem. Bull. South Ural. State Univ. Ser. Math. Model. Program. Comput. Soft. 2020, 13, 95–106. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulatov, K.; Chukalina, M.; Kutukova, K.; Kohan, V.; Ingacheva, A.; Buzmakov, A.; Arlazarov, V.V.; Zschech, E. Monitored Tomographic Reconstruction—An Advanced Tool to Study the 3D Morphology of Nanomaterials. Nanomaterials 2021, 11, 2524. https://doi.org/10.3390/nano11102524
Bulatov K, Chukalina M, Kutukova K, Kohan V, Ingacheva A, Buzmakov A, Arlazarov VV, Zschech E. Monitored Tomographic Reconstruction—An Advanced Tool to Study the 3D Morphology of Nanomaterials. Nanomaterials. 2021; 11(10):2524. https://doi.org/10.3390/nano11102524
Chicago/Turabian StyleBulatov, Konstantin, Marina Chukalina, Kristina Kutukova, Vlad Kohan, Anastasia Ingacheva, Alexey Buzmakov, Vladimir V. Arlazarov, and Ehrenfried Zschech. 2021. "Monitored Tomographic Reconstruction—An Advanced Tool to Study the 3D Morphology of Nanomaterials" Nanomaterials 11, no. 10: 2524. https://doi.org/10.3390/nano11102524