A Study on the Rotor Design of Line Start Synchronous Reluctance Motor for IE4 Efficiency and Improving Power Factor
Abstract
:1. Introduction
2. Characteristic of LS-SynRM
2.1. Structure of LS-SynRM
2.2. Asynchronous Speed
2.3. Synchronous Speed
3. Reference Machine
4. Design of LS-SynRM
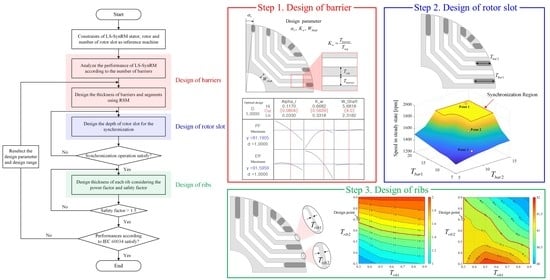
4.1. Design Process
4.2. Design of Barrier
4.2.1. Number of Barrier
4.2.2. Thickness of Flux Barriers and Segments
4.3. Design of Rotor Slot
4.4. Design of Ribs
4.5. Design Result
5. Experimental Validation
5.1. Manufacture of LS-SynRM
5.2. Experiment Result
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Almeida, A.T.D.; Ferreira, F.J.T.E.; Baoming, G. Beyond Induction Motors-Technology Trends to Move Up Efficiency. IEEE Ind. Appl. 2014, 50, 2103–2114. [Google Scholar]
- Almeida, A.T.D.; Ferreira, F.J.T.E.; Duarte, A.Q. Technical and Economical Considerations on Super High-Efficiency Three-Phase Motors. IEEE Ind. Appl. 2014, 50, 1274–1285. [Google Scholar]
- Ferreira, F.J.T.E.; Baoming, G.; Almeida, A.T.D. Reliability and Operation of High-Efficiency Induction Motors. IEEE Ind. Appl. 2016, 52, 4628–4637. [Google Scholar]
- Rafajdus, P.; Hrabovcova, V.; Lehocky, P.; Makys, P.; Holub, F. Effect of Saturation on Field Oriented Control of the New Designed Reluctance Synchronous Motor. Energies 2018, 11, 3223. [Google Scholar] [CrossRef] [Green Version]
- Aguba, V.; Muteba, M.; Nicolae, D.V. Transient Analysis of a Start-up Synchronous Reluctance Motor with Symmetrical Distributed Rotor Cage Bars. In Proceedings of the 2017 IEEE AFRICON, Cape Town, South Africa, 18–20 September 2017. [Google Scholar]
- Xie, Y.; Pi, C.; Li, Z. Study on Design and Vibration Reduction Optimization of High Starting Torque Induction Motor. Energies 2019, 12, 1263. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-J.; Hong, D.-K.; Choi, J.-H.; Chun, Y.-D.; Woo, B.-C.; Koo, D.-H. An Analytical Approach for a High Speed and High Efficiency Induction Motor Considering Magnetic and Mechanical Problems. IEEE Trans. Magn. 2013, 49, 2319–2322. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, H.; Zhang, Z.; Song, T. A Cast Copper Rotor Induction Motor for Small Commercial EV Traction: Electromagnetic Design, Analysis, and Experimental Tests. CES Trans. Electr. Mach. Syst. 2018, 2, 417–424. [Google Scholar] [CrossRef]
- Kazakbaev, V.; Prakht, V.; Dmitrievskii, V.; Ibrahim, M.N.; Oshurbekov, S.; Sarapulov, S. Efficiency Analysis of Low Electric Power Drives Employing Induction and Synchronous Reluctance Motors in Pump Applications. Energies 2019, 12, 1144. [Google Scholar] [CrossRef] [Green Version]
- Aarniovuori, L.; Kolehmainen, J.; Kosonen, A.; Niemela, M.; Chen, H.; Cao, W.; Pyrhonen, J. Application of Calorimetric Method for Loss Measurement of a SynRM Drive System. IEEE Trans. Ind. Electron. 2016, 64, 2005–2015. [Google Scholar] [CrossRef] [Green Version]
- Goetzler, W.; Sutherland, T.; Reis, C. Energy Savings Potential and Opportunities for High Efficiency Electric Motors in Residential and Commercial Equipment; United States Department of Energy: Washington, DC, USA, 2013. [Google Scholar]
- Ghoroghchian, F.; Aliabad, A.D.; Amiri, E. Design improvement of dual-pole LSPM synchronous motor. IET Electr. Power Appl. 2019, 13, 742–749. [Google Scholar] [CrossRef]
- Ghahfarokhi, M.M.; Aliabad, A.D.; Boroujeni, S.T.; Amiri, E.; Faradonbeh, V.Z. Analytical modelling and optimization of line start LSPM synchronous motors. IET Electr. Power Appl. 2020, 14, 398–408. [Google Scholar]
- Mingardi, D.; Bianchi, N. Line-Start PM-Assisted Synchronous Motor Design, Optimization, and Tests. IEEE Trans. Ind. Electron. 2017, 64, 9739–9747. [Google Scholar] [CrossRef]
- Liu, H.C.; Lee, J. Optimum Design of an IE4 Line-Start Synchronous Reluctance Motor Considering Manufacturing Process Loss Effect. IEEE Trans. Ind. Electron. 2018, 65, 3104–3114. [Google Scholar] [CrossRef]
- Tampio, J.; Kansakangas, T.; Suuriniemi, S.; Kolehmainen, J.; Kettunen, L.; Ikaheimo, J. Analysis of Direct-On-Line Synchronous Reluctance Machine Start-Up Using a Magnetic Field Decomposition. IEEE Trans. Ind. Appl. 2017, 53, 1852–1859. [Google Scholar]
- Liu, H.-C.; Hong, H.-S.; Cho, S.; Lee, J.; Jin, C.-S. Bubbles and Blisters Impact on Diecasting Cage to the Designs and Operations of Line-Start Synchronous Reluctance Motors. IEEE Trans. Magn. 2017, 53, 8202504. [Google Scholar] [CrossRef]
- Dent, P. Rare earth elements and permanent magnets. J. Appl. Phys. 2012, 111, 07A721. [Google Scholar] [CrossRef] [Green Version]
- Goss, J.; Popescu, M.; Staton, D. A comparison of an interior permanent magnet and copper rotor induction motor in a hybrid electric vehicle application. In Proceedings of the International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 220–225. [Google Scholar]
- Kazakbaev, V.; Parkht, V.; Dmitrievskii, V.; Oshurbekov, S.; Golovanov, D. Life Cycle Energy Cost Assessment for Pump Units with Various Types of Line-Start Operating Motors Including Cable Losses. Energies 2020, 13, 3546–3559. [Google Scholar]
- Kim, H.; Park, Y.; Liu, H.-C.; Han, P.-W.; Lee, J. Study on Line-Start Permanent Magnet Assistance Synchronous Reluctance Motor for Improving Efficiency and Power Factor. Energies 2020, 13, 384. [Google Scholar] [CrossRef] [Green Version]
- Joo, K.-J.; Kim, I.-G.; Lee, J.; Go, S.-C. Robust Speed Sensorless Control to Estimated Error for PMa-SynRM. IEEE Trans. Magn. 2017, 53, 8102604. [Google Scholar]
- Ozcelik, N.G.; Dogru, U.E.; Imeryuz, M.; Ergene, L.T. Synchronous Reluctance Motor vs. Induction Motor at Low-Power Industrial Applications: Design and Comparison. Energies 2019, 12, 2190. [Google Scholar] [CrossRef] [Green Version]
- Ogunjuyigbe, A.S.O.; Jimoh, A.A.; Ncolae, D.V.; Obe, E.S. Analysis of synchronous reluctance machine with magnetically coupled three-phase windings and reactive power compensation. IET Electr. Power Appl. 2010, 4, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Kersten, A.; Liu, Y.; Pehrman, D.; Thiringer, T. Rotor Design of Line-Start Synchronous Reluctance Machine With Round Bars. IEEE Ind. Appl. 2019, 55, 3685–3696. [Google Scholar] [CrossRef]
- Gamba, M.; Pellegrino, G.; Vagati, A.; Villata, F. Design of a Line-Start Synchronous Reluctance Motor. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013. [Google Scholar]
- Pellegrino, G.; Cupertino, F.; Gerada, C. Automatic Design of Synchronous Reluctance Motors Focusing on Barrier Shape Optimization. IEEE Trans. Ind. Appl. 2015, 51, 1465–1474. [Google Scholar] [CrossRef]
- Kim, K.-C.; Ahn, J.S.; Won, S.H.; Hong, J.-P.; Lee, J. A Study on the Optimal Design of SynRM for the High Torque and Power Factor. IEEE Trans. Magn. 2007, 43, 2543–2545. [Google Scholar] [CrossRef]
- Liu, H.C.; Seol, H.S.; Kim, J.Y.; Lee, J. Design and Analysis of an IE4 Class Line-Start Synchronous Reluctance Motor Considering Total Loss and Starting Performance. J. Electron. Mater. 2019, 48, 1386–1394. [Google Scholar] [CrossRef]
- Wang, Y.; Chau, K.T.; Chan, C.C.; Jiang, J.Z. Transient Analysis of a New Outer-Rotor Permanent-Magnet Brushless DC Drive Using Circuit-Field-Torque Coupled Time-Stepping Finite-Element Method. IEEE Trans. Magn. 2002, 38, 1297–1300. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-K.; Jung, D.-H.; Lim, J.; Lee, K.-D.; Lee, J. A Study on the Synchronous Reluctance Motor Design for High Torque by Using RSM. IEEE Trans. Magn. 2018, 54, 8103005. [Google Scholar] [CrossRef]















| Item | Value | Unit |
|---|---|---|
| Output power | 2.2 | kW |
| Line voltage | 380 | Vrms |
| Input frequency | 60 | Hz |
| Outer diameter (stator/rotor) | 180/109.4 | mm |
| Inner diameter (stator/rotor) | 110/32 | mm |
| Number of slot (stator/rotor) | 36/28 | – |
| Stack length | 120 | mm |
| Air gap length | 0.3 | mm |
| Item | Value | Unit | |
|---|---|---|---|
| FEA | Experiment | ||
| Power | 2.2 | 2.2 | kW |
| Speed | 1764.96 | 1762 | rpm |
| Torque | 12 | 11.9 | Nm |
| Core loss | 58.27 | 63 | W |
| Stator copper loss | 72.6 | 78 | W |
| Rotor copper loss | 40.53 | 51 | W |
| Total loss | 214.3 | 220 | W |
| Efficiency | 91.2 | 90.7 | % |
| Power factor | 83.8 | 80 | % |
| Items | IEC 60034 | Design Objective | Unit | |
|---|---|---|---|---|
| Performance | Efficiency | 91 | ≥91.5 | % |
| Power factor | 77 | ≥81 | % | |
| Model | Ld (mH) | Lq (mH) | Saliency Ratio | Power Factor (%) |
|---|---|---|---|---|
| Model 1 | 33.6 | 301.6 | 8.97 | 78.7 |
| Model 2 | 31.7 | 297.7 | 9.38 | 79.3 |
| Model 3 | 31.2 | 309.5 | 9.92 | 80.5 |
| Items | αr (degM) | Kw | Wshaft (mm) |
|---|---|---|---|
| Range | 4.5–9 | 0.4–0.6 | 3–6 |
| Parameter | Power Factor (%) | Efficiency (%) | ||||
|---|---|---|---|---|---|---|
| αr(degM) | Kw | Wshaft(mm) | RSM | FEA | RSM | FEA |
| 7.236 | 0.5609 | 4 | 81.19 | 81.02 | 91.59 | 91.75 |
| Item | Value | Unit |
|---|---|---|
| Power | 2.2 | kW |
| Speed | 1800 | rpm |
| Torque | 11.7 | Nm |
| Core loss | 53.3 | W |
| Stator copper loss | 87.78 | W |
| Rotor copper loss | 12.3 | W |
| Total loss | 201.4 | W |
| Efficiency | 91.7 | % |
| Power factor | 81.2 | % |
| Safety factor | 1.56 | - |
| Item | Value | Unit | |
|---|---|---|---|
| FEA | Experiment | ||
| Power | 2.2 | 2.2 | kW |
| Torque | 11.7 | 11.6 | Nm |
| Current | 4.56 | 4.8 | Arms |
| Core loss | 53.3 | 45.9 | W |
| Stator copper loss | 87.78 | 100 | W |
| Rotor copper loss | 12.3 | 0 | W |
| Total loss | 201.4 | 201.7 | W |
| Efficiency | 91.7 | 91.6 | % |
| Power factor | 81.2 | 77.3 | % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Park, Y.; Oh, S.-T.; Jang, H.; Won, S.-H.; Chun, Y.-D.; Lee, J. A Study on the Rotor Design of Line Start Synchronous Reluctance Motor for IE4 Efficiency and Improving Power Factor. Energies 2020, 13, 5774. https://doi.org/10.3390/en13215774
Kim H, Park Y, Oh S-T, Jang H, Won S-H, Chun Y-D, Lee J. A Study on the Rotor Design of Line Start Synchronous Reluctance Motor for IE4 Efficiency and Improving Power Factor. Energies. 2020; 13(21):5774. https://doi.org/10.3390/en13215774
Chicago/Turabian StyleKim, Hyunwoo, Yeji Park, Seung-Taek Oh, Hyungkwan Jang, Sung-Hong Won, Yon-Do Chun, and Ju Lee. 2020. "A Study on the Rotor Design of Line Start Synchronous Reluctance Motor for IE4 Efficiency and Improving Power Factor" Energies 13, no. 21: 5774. https://doi.org/10.3390/en13215774