Johnson–Holmquist-II(JH-2) Constitutive Model for Rock Materials: Parameter Determination and Application in Tunnel Smooth Blasting
Abstract
:1. Introduction
2. JH-2 Constitutive Model for Rock Materials
2.1. Strength
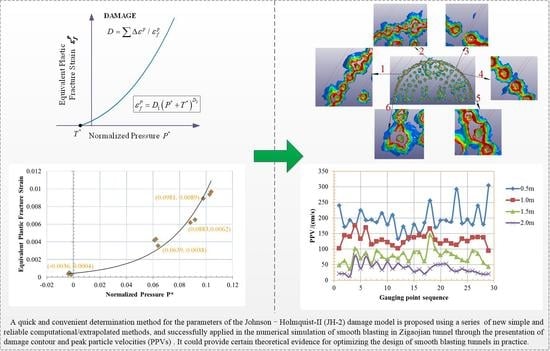
2.2. Damage
2.3. Polynomial Equation of State (EOS) of Pressure
3. Parameter Determination Method for the JH-2 Model
3.1. Determination of Parameters Concerned with HEL
3.2. Determination of EOS Parameters
3.3. Determination of Strength
3.3.1. Determination of Intact Strength
3.3.2. Determination of Fractured Strength
3.4. Determination of Damage
4. Application in Tunnel Smooth Blasting
4.1. 3D Numerical Modelling of Smooth Blasting Tunnel
4.2. Relation between Crucial Damage Zone and Practical Overbreak
4.3. Damage Influenced by Bedded Joints
4.4. Damage in Large Scope Estimated by PPV
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the Seventh International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; Volume 21, pp. 541–547. [Google Scholar]
- Johnson, G.R.; Holmquist, T.J. A computational constitutive model for brittle materials subjected to large strains, high strain rates and high pressures. In Shock Wave and High-Strain-Rate Phenomena in Materials; Meyers, M., Murr, L., Staudhammer, K., Eds.; CRC Press: Boca Raton, FL, USA, 1992; pp. 1075–1081. [Google Scholar]
- Johnson, G.R.; Holmquist, T.J. An improved computational constitutive model for brittle materials. In AIP Conference of High-Pressure Science and Technology; Schmidt, S.C., Shaner, J.W., Samara, G.A., Eds.; American Institute of Physics: Colorado Springs, CO, USA, 1994; Volume 309, pp. 981–984. [Google Scholar]
- Johnson, G.R.; Holmquist, T.J. Response of boron carbide subjected to large strains, high strain rates, and high pressures. J. Appl. Phys. 1999, 85, 8060–8073. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J.; Beissel, S.R. Response of aluminum nitride (including a phase change) to large strains, high strain rates, and high pressures. J. Appl. Phys. 2003, 94, 1639–1646. [Google Scholar] [CrossRef]
- Nguyen, G.D.; Einav, I.; Guiamatsia, I. On the partition of fracture energy in constitutive modelling of quasi-brittle materials. Eng. Fract. Mech. 2012, 79, 225–244. [Google Scholar] [CrossRef]
- Zhou, X.P.; Yang, H.Q. Micromechanical modeling of dynamic compressive responses of mesoscopic heterogenous brittle rock. Theor. Appl. Fract. Mech. 2007, 48, 1–20. [Google Scholar] [CrossRef]
- Tryding, J.; Ristinmaa, M. Normalization of cohesive laws for quasi-brittle materials. Eng. Fract. Mech. 2017, 178, 333–345. [Google Scholar] [CrossRef]
- Varadarajan, A.; Sharma, K.G.; Abbas, S.M.; Dhawan, A.K. Constitutive model for rockfill materials and determination of material constants. Int. J. Geomech. 2006, 6, 226–237. [Google Scholar] [CrossRef]
- Desai, C.S.; Chen, J.Y. Parameter optimization and sensitivity analysis for disturbed state constitutive model. Int. J. Geomech. 2006, 6, 75–88. [Google Scholar] [CrossRef]
- Ruggiero, A.; Iannitti, G.; Bonora, N.; Ferraro, M. Determination of Johnson-holmquist constitutive model parameters for fused silica. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2012; Volume 26, p. 04011. [Google Scholar]
- Fang, Q.; Kong, X.Z.; Wu, H.; Gong, Z.M. Determination of Holmquist-Johnson-Cook constitutive model parameters of rock. Eng. Mech. 2014, 31, 197–204. (In Chinese) [Google Scholar]
- Holmquist, T.J.; Johnson, G.R.; Lopatin, C.M.; Grady, D.E.; Hertel, E.S., Jr. High strain rate properties and constitutive modeling of glass. In Proceedings of the 15th International Symposium on Ballistics, Jerusalem, Israel, 21–24 May 1995. [Google Scholar]
- Holmquist, T.J.; Johnson, G.R.; Cook, W.H. A constitutive model and data for concrete subjected to large strains, high strain rates and high pressures. In Proceedings of the 14th International Symposium on Ballistics, Quebec City, QC, Canada, 26–29 September 1993. [Google Scholar]
- Meyer, C.S. Development of geomaterial parameters for numerical simulations using the Holmquist-Johnson-Cook constitutive model for concrete. In Proceedings of the Army Research Lab Aberdeen Proving Ground MD Weapons and Materials Research Directorate, Adelphi, MD, USA, 14–16 June 2011. [Google Scholar]
- Islam, M.J.; Swaddiwudhipong, S.; Liu, Z.S. Penetration of concrete targets using a modified Holmquist-Johnson-Cook material model. Int. J. Comput. Methods 2012, 9, 1250056. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Templeton, D.W.; Bishnoi, K.D. Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications. Int. J. Impact Eng. 2001, 25, 211–231. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R. Characterization and evaluation of boron carbide for plate-impact conditions. J. Appl. Phys. 2006, 100, 093525. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R. Response of boron carbide subjected to high-velocity impact. Int. J. Impact Eng. 2008, 35, 742–752. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R. A computational constitutive model for glass subjected to large strains, high strain rates and high pressures. J. Appl. Mech. 2011, 78, 051003. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; Zhang, X.L.; Zhao, J. Two-dimensional DDA contact constitutive model for simulating rock fragmentation. J. Eng. Mech. 2011, 138, 199–209. [Google Scholar] [CrossRef]
- Yu, T. Statistical damage constitutive model of quasi-brittle materials. J. Aerosp. Eng. 2009, 22, 95–100. [Google Scholar] [CrossRef]
- Li, X.; Cao, W.G.; Su, Y.H. A statistical damage constitutive model for softening behavior of rocks. Eng. Geol. 2012, 143, 1–17. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, C.; Zhao, M.; Li, X. Statistical damage constitutive model for rocks considering residual strength. Int. J. Geomech. 2016, 17, 04016033. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Ayatollahi, M.R.; Berto, F. A synthesis of geometry effect on brittle fracture. Eng. Fract. Mech. 2018, 187, 94–102. [Google Scholar] [CrossRef]
- Ai, H.A.; Ahrens, T.J. Simulation of dynamic response of granite: A numerical approach of shock-induced damage beneath impact craters. Int. J. Impact Eng. 2006, 33, 1–10. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical simulation of blasting-induced rock fractures. Int. J. Rock Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Wei, X.Y.; Zhao, Z.Y.; Gu, J. Numerical simulations of rock mass damage induced by underground explosion. Int. J. Rock Mech. Min. Sci. 2009, 46, 1206–1213. [Google Scholar] [CrossRef]
- Banadaki, M.M.D. Stress-Wave Induced Fracture in Rock Due to Explosive Action. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2010. [Google Scholar]
- Banadaki, M.M.D.; Mohanty, B. Numerical simulation of stress wave induced fractures in rock. Int. J. Impact Eng. 2012, 40, 16–25. [Google Scholar] [CrossRef]
- He, C.; Yang, J. Dynamic crack propagation of granite subjected to biaxial confining pressure and blast loading. Lat. Am. J. Solids Struct. 2018, 15, e45. [Google Scholar] [CrossRef]
- Xia, Y.M.; Guo, B.; Cong, G.Q.; Zhang, X.H.; Zeng, G.Y. Numerical simulation of rock fragmentation induced by a single TBM disc cutter close to a side free surface. Int. J. Rock Mech. Min. 2017, 91, 40–48. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.B.; Zhao, J. Numerical Simulation of Rock Dynamic Failure by Particle-Based Numerical Manifold Method. In 22nd DYMAT Technical Meeting, Grenoble; Atlas Copco: Stockholm, Sweden, 2016. [Google Scholar]
- Li, X.; Zhang, Q.B.; He, L.; Zhao, J. Particle-based numerical manifold method to model dynamic fracture process in rock blasting. Int. J. Geomech. 2016, 17, E4016014. [Google Scholar] [CrossRef]
- Gharehdash, S.; Shen, L.; Gan, Y.; Flores-Johnson, E.A. Numerical investigation on fracturing of rock under blast using coupled finite element method and smoothed particle hydrodynamics. Appl. Mech. Mater. 2016, 846, 102–107. [Google Scholar] [CrossRef]
- Gross, D.; Seelig, T. Elastic-plastic fracture mechanics. In Fracture Mechanics. Mechanical Engineering Series; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Goldsmith, W.; Sackman, J.L.; Ewerts, C. Static and dynamic fracture strength of Barre granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1976, 13, 303–309. [Google Scholar] [CrossRef]
- Shang, J.L.; Shen, L.T.; Zhao, J. Hugoniot equation of state of the Bukit Timah granite. Int. J. Rock Mech. Min. Sci. 2000, 37, 705–713. [Google Scholar] [CrossRef]
- Gautam, P.C.; Gupta, R.; Sharma, A.C.; Singh, M. Determination of Hugoniot Elastic Limit (HEL) and Equation of State (EOS) of Ceramic Materials in the Pressure Region 20 GPa to 100 GPa. Proc. Eng. 2017, 173, 198–205. [Google Scholar] [CrossRef]
- Kingsbury, S.J.; Tsembelis, K.; Proud, W.G. The dynamic properties of the Atlanta Stone Mountain granite. Proc. AIP Conf. 2004, 706, 1454–1457. [Google Scholar]
- Petersen, C.F. Shock Wave Studies of Selected Rocks. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1969; p. 99. [Google Scholar]
- Nellis, W.J. Dynamic compression of materials: Metallization of fluid hydrogen at high pressures. Rep. Prog. Phys. 2006, 69, 1479. [Google Scholar] [CrossRef]
- Gebbeken, N.; Greulich, S.; Pietzsch, A. Determination of shock equation of state properties of concrete using full-scale experiments and flyer-plate-impact tests. In Proceedings of the Trends in Computational Structural Mechanics, Barcelona, Spain, 20–23 May 2001; Wall, W.A., Bletzinger, K.U., Schweizerhof, K., Eds.; CIMNE: Barcelona, Spain; pp. 109–117. [Google Scholar]
- Gebbeken, N.; Greulich, S.; Pietzsch, A. Hugoniot properties for concrete determined by full-scale detonation experiments and flyer-plate-impact tests. Int. J. Impact Eng. 2006, 32, 2017–2031. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Du, X.L.; Ma, C.; Lu, D.C. Effect of hydrostatic pressure on geomaterials. CJRME 2015, 34, 572–582. (In Chinese) [Google Scholar]
- Yang, Z.Q.; Pang, B.J.; Wang, L.W.; Chi, R.Q. JH-2 model and its application to numerical simulation on Al2O3 ceramic under low-velocity impact. Explos. Shock Waves 2010, 30, 463–471. (In Chinese) [Google Scholar]
- Yuan, F.; Prakash, V. Plate impact experiments to investigate shock-induced inelasticity in Westerly granite. Int. J. Rock Mech. Min. Sci. 2013, 60, 277–287. [Google Scholar] [CrossRef] [Green Version]
- Cronin, D.S.; Bui, K.; Kaufmann, C.; McIntosh, G.; Berstad, T.; Cronin, D. Implementation and validation of the Johnson-Holmquist ceramic material model in LS-Dyna. In Proceedings of the 4th European LS-DYNA Users Conference, Ulm, Germany, 22–23 May 2003; Volume 500, pp. 47–60. [Google Scholar]
- Xia, K.; Nasseri, M.H.B.; Mohanty, B.; Lu, F.; Chen, R.; Luo, S.N. Effects of microstructures on dynamic compression of Barre granite. Int. J. Rock Mech. Min. Sci. 2008, 45, 879–887. [Google Scholar] [CrossRef]
- Martin, C.D. Seventeenth Canadian geotechnical colloquium: The effect of cohesion loss and stress path on brittle rock strength. Can. Geotech. J. 1997, 34, 698–725. [Google Scholar] [CrossRef]
- Fakhimi, A.; Lanari, M. DEM–SPH simulation of rock blasting. Comput. Geotech. 2014, 55, 158–164. [Google Scholar] [CrossRef]
- Wang, J.; Yin, Y.; Esmaieli, K. Numerical Simulations of Rock Blasting Damage Based on Laboratory Scale Experiments. J. Geophys. Eng. 2018, 15, 2399–2417. [Google Scholar] [CrossRef]
- Hoek, E. The development of rock engineering. In Practical Rock Engineering; Rocscience: Toronto, ON, Canada, 2007; pp. 11–13. [Google Scholar]
- Abbas, S.M.; Konietzky, H. Rock mass classification systems. In Introduction to Geomechanics, Department of Rock Mechanics, Technical University Freiberg (Ebook); Freiberg University of Mining and Technology: Freiberg, Germany, 2014. [Google Scholar]
- Bieniawski, Z.T. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 335–343. [Google Scholar]
- Bieniawski, Z.T.; Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons, Inc.: New York, NY, USA, 1989; ISBN 0-471-60172-1. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Barton, N.; Grimstad, E. Rock mass conditions dictate choice between NMT and NATM. Tunn. Tunn. Int. 1994, 26, 39–42. [Google Scholar]
- GB/T50218. Engineering Rock Mass Classification Standard; China National Standards: Beijing, China, 2014. (In Chinese) [Google Scholar]
- TB 10003. Code for Design of Railway Tunnel; China National Standards: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Jin, L.; Lu, W.B.; Chen, M. Mechanism of jointed rock loosing under blasting load. Explos. Shock Waves 2009, 29, 474–480. (In Chinese) [Google Scholar]
- Singh, S.P.; Xavier, P. Causes, impact and control of overbreak in underground excavations. Tunn. Undergr. Space Technol. 2005, 20, 63–71. [Google Scholar] [CrossRef]
- Jang, H.; Topal, E. Optimizing overbreak prediction based on geological parameters comparing multiple regression analysis and artificial neural network. Tunn. Undergr. Space Technol. 2013, 38, 161–169. [Google Scholar] [CrossRef]
- Zhao, M.J.; Sun, X.; Wang, S. Damage evolution analysis and pressure prediction of surrounding rock of a tunnel based on rock mass classification. EJGE 2014, 19, 603–627. [Google Scholar]
- Tang, S.; Yu, C.; Tang, C. Numerical modeling of the time-dependent development of the damage zone around a tunnel under high humidity conditions. Tunn. Undergr. Space Technol. 2018, 76, 48–63. [Google Scholar] [CrossRef]
- Murthy, V.M.S.R.; Dey, K.; Raitani, R. Prediction of overbreak in underground tunnel blasting: A case study. J. Can. Tunn. Can. 2003, 109–115. [Google Scholar]
- Saiang, D. Stability analysis of the blast-induced damage zone by continuum and coupled continuum-discontinuum methods. Eng. Geol. 2010, 116, 1–11. [Google Scholar] [CrossRef]
- Huang, F.; Zhu, H.; Jiang, S.; Liang, B. Excavation-damaged zone around tunnel surface under different release ratios of displacement. Int. J. Geomech. 2016, 17, 04016094. [Google Scholar] [CrossRef]
- Souissi, S.; Miled, K.; Hamdi, E.; Sellami, H. Numerical Modeling of Rock Damage during Indentation Process with Reference to Hard Rock Drilling. Int. J. Geomech. 2017, 17, 04017002. [Google Scholar] [CrossRef]
- Persson, P.A. The relationship between strain energy, rock damage, fragmentation, and throw in rock blasting. Fragblast 1997, 1, 99–110. [Google Scholar] [CrossRef]
- Li, Z.; Huang, H. The calculation of stability of tunnels under the effects of seismic wave of explosions. In 26th Department of Defence Explosives Safety Seminar, USA, Department of Defence Explosives Safety Board; Doral Resort: Miami, FL, USA, 1994. [Google Scholar]


















| Constants | Barre Granite | Sandstone | Constants | Barre Granite | Sandstone |
|---|---|---|---|---|---|
| Density () | 2.66 | 2.60 | Hugoniot elastic limit HEL () | 4.5 | 4.5 |
| Shear modulus () | 21.9 | 17.8 | HEL pressure () | 2.93 | 2.6 |
| Intact strength coefficient | 1.248 | 1.01 | Bulk factor | 1.0 | 1.0 |
| Fractured strength coefficient | 0.68 | 0.68 | Damage coefficient | 0.008 | 0.005 |
| Strain rate coefficient | 0.0051 | 0.005 | Damage coefficient | 0.435 | 0.7 |
| Fractured strength exponent | 0.83 | 0.83 | Bulk modulus () | 25.7 | 19.5 |
| Intact strength exponent | 0.676 | 0.83 | Second pressure coefficient () | −386 | −23 |
| Maximum tensile strength () | 57 | 45 | Third pressure coefficient () | 12,800 | 2980 |
| Maximum normalized fractured strength | 0.16 | 0.18 | |||
| Explosive | A/105 MPa | B/105 MPa | R1 | R2 | ω | V0 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| E. 1 | 1.60 | 0.550 | 0.096 | 5.576 | 0.0535 | 6.1 | 1.07 | 0.24 | 0.041 | 1.0 |
| E. 2 | 1.26 | 0.527 | 0.081 | 5.576 | 0.0535 | 6.1 | 1.07 | 0.24 | 0.041 | 1.0 |
| Distance (m) | PPV Concentrated Range (cm/s) | Average PPV (cm/s) | Damage Degree |
|---|---|---|---|
| 0.5 m | 150–250 | 196.3 | Serious damage |
| 1.0 m | 100–150 | 130.2 | Medium/serious damage |
| 1.5 m | 50–100 | 76.8 | Slight/medium damage |
| 2.0 m | 30–50 | 38.1 | Basically no damage |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yin, Y.; Luo, C. Johnson–Holmquist-II(JH-2) Constitutive Model for Rock Materials: Parameter Determination and Application in Tunnel Smooth Blasting. Appl. Sci. 2018, 8, 1675. https://doi.org/10.3390/app8091675
Wang J, Yin Y, Luo C. Johnson–Holmquist-II(JH-2) Constitutive Model for Rock Materials: Parameter Determination and Application in Tunnel Smooth Blasting. Applied Sciences. 2018; 8(9):1675. https://doi.org/10.3390/app8091675
Chicago/Turabian StyleWang, Jianxiu, Yao Yin, and Chuanwen Luo. 2018. "Johnson–Holmquist-II(JH-2) Constitutive Model for Rock Materials: Parameter Determination and Application in Tunnel Smooth Blasting" Applied Sciences 8, no. 9: 1675. https://doi.org/10.3390/app8091675