Numerical Solution of Casson Nanofluid Flow Over a Non-linear Inclined Surface With Soret and Dufour Effects by Keller-Box Method

Anwar, Muhammad Imran; Rafique, Khurram; Misiran, Masnita; Khan, Ilyas

doi:10.3389/fphy.2019.00139

ORIGINAL RESEARCH article

Front. Phys., 11 October 2019
Sec. Statistical and Computational Physics
Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00139

Numerical Solution of Casson Nanofluid Flow Over a Non-linear Inclined Surface With Soret and Dufour Effects by Keller-Box Method

Khuram Rafique¹

Muhammad Imran Anwar^1,2,3

Masnita Misiran¹

Ilyas Khan⁴^*

S. O. Alharbi⁵

Phatiphat Thounthong⁶

K. S. Nisar⁷

¹School of Quantitative Sciences, Universiti Utara Malaysia, Sintok, Malaysia
²Department of Mathematics, Faculty of Science, University of Sargodha, Sargodha, Pakistan
³Higher Education Department (HED) Punjab, Lahore, Pakistan
⁴Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
⁵Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al Majmaah, Saudi Arabia
⁶Department of Teacher Training in Electrical Engineering, Faculty of Technical Education, Renewable Energy Research Centre, King Mongkut's University of Technology North Bangkok, Bang Sue, Thailand
⁷Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Al Dawasir, Saudi Arabia

In this article, the effects of a Casson Nanofluid boundary layer flow, over an inclined extending surface with Soret and Dufour, is scrutinized. The model used in this study is based on the Buongiorno model of the thermal efficiencies of the fluid flows in the presence of Brownian motion and thermophoresis properties. The non-linear problem for Casson Nanofluid flow over an inclined channel is modeled to gain knowledge on the heat and mass exchange phenomenon, by considering important flow parameters of the intensified boundary layer. The governing non-linear partial differential equations are changed to non-linear ordinary differential equations and are afterward illustrated numerically by the Keller-Box scheme. A comparison of the established results, if the incorporated effects are lacking, is performed with the available outcomes of Khan and Pop [1] and recognized in a nice settlement. Numerical and graphical results are also presented in tables and graphs.

Introduction

In recent times, nanofluid has accomplished an incredible position among scientists because of its dynamic thermal performance and notable potential in the number of heat transfers without any pressure drops. Nanofluid is a formula of various nanoparticles, containing Al₂O₃, Cu, CuO, in a base liquid, for example, oil, water, ethylene glycol, and so forth. It is investigated through examination that the thermal conductivity of base fluid is usually not exactly the same as the nanofluid Choi and Eastman [2]. Nanofluid is used as a working fluid (base fluid) due to its high thermal conductivity. Buongiorno [3] examined the causes that perform a key job in the advancement of nanofluid's thermal conductivity. He perceived that the Brownian movement and thermophoresis effects in conventional fluid play an important role to enhance the thermal conductivity of the fluid. Nield and Kuznetsov [4] considered the result of thermophoresis and Brownian movement on the boundary layer stream. The steady flow of nanofluid on an extending sheet was examined by Khan and Pop [1]. Anwar et al. [5] presented the Brownian movement and thermophoresis impact on the heat and mass exchange of nanofluids over a non-linear extending sheet. Suriyakumar and Devi [6] examined the nanofluid flow over a slanted sheet. Ziaei-Rad et al. [7] investigated a similar solution of nanofluid stream on a slanted surface. Thumma et al. [8] discussed the nanofluid flow on a slanted plate by incorporating the heat source. Govindarajan [9] discussed the flow of nanofluid over a slanted sheet by incorporating a non-uniform temperature. Khan et al. [10] illustrated the heat and mass transfer of MHD Jeffery nanofluid flow over an inclined sheet. Nanofluid flow with radiation effects on a slanted surface was examined by Chakraborty [11]. Recently, different scholars investigated the nanofluid flow on different models, as some of them are given in references [12–18].

The investigation of boundary layer flow and heat exchange on a stretching surface has been considered by various experts due to its immense mechanical and designing applications in the field of industry, and engineering, for example, strengthening and tinning of copper wires, assembling plastic and elastic sheets, non-stop cooling and fiber turning, expulsion of polymer, wire drawing, food processing, and paper, and so forth. Boundary layer flow on a steady surface was first investigated by Sakiadis [19]. Additionally, Crane [20] considered the closed structure solution of boundary layer flow on an extending sheet. Ali et al. [21] investigated the conjugate effects of heat and mass exchange on MHD free convection flow over an inclined plate. Ramesh et al. [22] investigated the boundary layer flow over the slanted sheet with convective boundaries. MHD free convection dissipative fluid stream past over an inclined sheet was investigated by Malik [23]. The boundary layer flow on a slanted sheet through convective boundaries was discussed by Ramesh et al. [24]. Griffiths [25] investigated the non-Newtonian boundary layer flow over a slanted sheet. Soret and Dufour effect over a slanted plate was discussed by Pal and Mondal [26]. Pandya and Shukla [27] investigated the unsteady MHD flow over a slanted surface by taking viscous dissipations. Thermal radiation impacts are important in solar plants [28].

In 1959, Casson offered the Casson fluid model for the flow of viscoelastic liquids. Casson fluid is a shear thinning fluid which should have zero viscosity at an infinite rate of shear and infinite viscosity at zero rates of shear, yielding stress under which no flow takes place. Some examples of Casson fluid are, honey, jelly, sauce, soup etc. [29] Ali et al. [30] examined the Casson fluid flow on a slanted sheet by incorporating the Soret-Dufour effects. Manideep et al. [31] studied the Casson fluid flow on vertically inclined sheets. Shamshuddin et al. [32] numerically investigated the effect of chemical reaction on Casson fluid flow on a slanted plate. Casson fluid flow over a slanted plate calculated by Vijayaragavan and Kavitha [33]. Prasad et al. [34] investigated the Casson fluid flow over an inclined sheet by considering the hall current. Jain and Parmar [35] studied the inclined Casson fluid flow on a permeable sheet. Sailaja et al. [36] studied the Casson fluid flow on a vertical sheet by incorporating the angle effect. Rawi et al. [37] discussed the Casson fluid flow over a slanted sheet by considering nanoparticles. Rauju et al. [38] discussed the Casson fluid flow on a vertically slanted sheet. The Casson fluid model is more compatible with blood flow simulation [39, 40].

Persuaded by the above referred literature review, and due to the growing needs of non-Newtonian nanofluid flows in industry and engineering areas, the present work focuses on the Casson nanofluid flow over a non-linear inclined stretching surface with Soret and Dufour effects. Casson nanofluid is more helpful for cooling and friction reducing agents compared to Newtonian based nanofluid flow [15]. To the best of the author's knowledge, the solution of the Casson nanofluid flow over a non-linear inclined stretching surface with radiation, as well as Soret and Dufour effects with the Keller-Box method, has not yet been reported. The model under consideration is newly developed from Khan and Pop [1] and results obtained from the current study are new. In this work, we found that the Dufour effect reduces the Nusselt and Sherwood number due to Soret impact. A non-linear form of radiative heat exchange also enhances the fluid temperature. This study is very useful in nuclear reactors, MHD generators, and in geothermal energy. In the future, it can be extended on an exponentially inclined stretching surface.

Problem Formulation

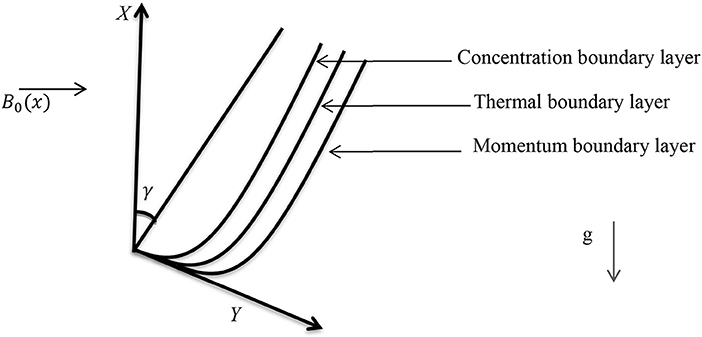
A steady, two-dimensional boundary layer flow of Casson Nano fluid over a non-linear slanted extending surface on angle γ is considered. The extending and free stream velocities are taken as, $u_{w} (x) = a x^{m}$ and u_∞(x) = 0. Where, “x” is the coordinate dignified in the direction of the extending surface with “a” supposed constant. An external transverse magnetic field is assumed normal to the flow path. The Brownian motion and thermophoresis effects are considered. The temperature T and Nano particle fraction C at the wall take the constant values T_w and C_w, while the ambient forms for the nanofluid mass and temperature fractions C_∞ and T_∞ are accomplished as y approaches to immensity, as shown in Figure 1.

FIGURE 1

Figure 1. Physical geometry and coordinate system.

The flow equations for this study [1] are given by:

\begin{array}{l} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 & (1) \end{array}

\begin{array}{l} u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = ν (1 + \frac{1}{β}) \frac{\partial^{2} u}{\partial y^{2}} + g [β_{t} (T - T_{\infty}) \\ + β_{c} (C - C_{\infty})] c o s γ - \frac{σ {B_{0}}^{2} (x) u}{ρ} & (2) \end{array}

\begin{array}{l} u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = α \frac{\partial^{2} T}{\partial y^{2}} - \frac{1}{{(δ c)}_{f}} \frac{\partial q_{r}}{\partial y} + τ [D_{B} \frac{\partial C}{\partial y} \frac{\partial T}{\partial y} \\ + \frac{D_{T}}{T_{\infty}} {(\frac{\partial T}{\partial y})}^{2}] + \frac{D_{T} K_{T}}{C_{s} C_{p}} \frac{\partial^{2} C}{\partial y^{2}}, & (3) \end{array}

\begin{array}{l} u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y} = D_{B} \frac{\partial^{2} C}{\partial y^{2}} + \frac{D_{T} K_{T}}{T_{\infty}} \frac{\partial^{2} T}{\partial y^{2}}, & (4) \end{array}

Here, the Rosseland approximation (for radiation flux) is defined as:

\begin{array}{l} q r = - \frac{4 σ^{*}}{3 k^{*}} \frac{\partial T^{4}}{\partial y}, & (5) \end{array}

Where, σ^* is the Stefan-Boltzmann constant and k^* is the mean absorption coefficient. It is assumed that the temperature difference between the free steam T_∞ and local temperature T is small enough, expanding T⁴ in Taylor series about T_∞ and neglecting higher order terms for:

\begin{array}{l} T^{4} ≅ 4 T_{\infty}^{3} T - 3 T_{\infty}^{4}, & (6) \end{array}

Using Equations (5) and (6) the Equation (3) converts into:

\begin{array}{l} u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = (α + \frac{16 σ^{*}}{3 k^{*} {(δ c)}_{f}}) \frac{\partial^{2} T}{\partial y^{2}} + τ [D_{B} \frac{\partial C}{\partial y} \frac{\partial T}{\partial y} \\ + \frac{D_{T}}{T_{\infty}} {(\frac{\partial T}{\partial y})}^{2}] + \frac{D_{T} K_{T}}{C_{s} C_{p}} \frac{\partial^{2} C}{\partial y^{2}}, & (7) \end{array}

Where u and v are the velocity components in the x and y directions, respectively, g is the acceleration due to gravity, B₀ is the uniform magnetic field strength, σ is the electrical conductivity, u is the viscosity, δ_f is the density of the base fluid, δ_p is the density of the nanoparticle, β is the Casson parameter, β_t is the coefficient of thermal expansion, β_c is the coefficient of concentration expansion, D_B is the Brownian diffusion coefficient and D_T is the thermophoresis diffusion coefficient, k is the thermal conductivity, (δc)_p is the heat capacitance of the nanoparticles, (δc)_f is the heat capacitance of the base fluid, $α = \frac{k}{{(δ c)}_{f}}$ is the thermal diffusivity parameter, $τ = \frac{{(δ c)}_{p}}{{(δ c)}_{f}}$ is the ratio between the effective heat capacity of the nanoparticle and heat capacity of the fluid.

The subjected boundary conditions are:

\begin{array}{l} u = u_{w} (x) = a x^{m}, v = 0, T = T_{w}, C = C_{w} a t y = 0, \\ u \to u_{\infty} (x) = 0, v \to 0, T \to T_{\infty}, C \to C_{\infty} a t y \to \infty, n & (8) \end{array}

The non-linear partial differential equations are reduced into non-linear ordinary differential equations. For that purpose, the stream function ψ = ψ(x, y) is defined as:

\begin{array}{l} u = \frac{\partial ψ}{\partial y}, v = - \frac{\partial ψ}{\partial x}, & (9) \end{array}

continuity (Equation 1) is satisfied identically.

The similarity transformations are defined as:

\begin{array}{l} ψ = \sqrt{\frac{2 v a x^{m + 1}}{m + 1}} f (η), θ (η) = \frac{T - T_{\infty}}{T_{w} - T_{\infty}}, \\ ϕ (η) = \frac{C - C_{\infty}}{C_{w} - C_{\infty}}, η = y \sqrt{\frac{(m + 1) a x^{m - 1}}{2 v}} . & (10) \end{array}

On substituting (Equation 7), system of Equations (2), (3), and (7) reduce to the following non-linear ordinary differential equations:

\begin{array}{l} (1 + \frac{1}{β}) f^{‴} + f f^{″} - (\frac{2 m}{m + 1}) f^{'} 2 + \frac{2}{m + 1} (λ θ - δ ϕ) c o s γ \\ - (\frac{2 M}{m + 1}) f^{'} = 0 & (11) \end{array}

\begin{array}{l} P r_{N} θ^{″} + f θ^{'} + N_{b} ϕ^{'} θ^{'} + N_{t} {θ^{'}}^{2} + D_{f} ϕ^{″} = 0 & (12) \end{array}

\begin{array}{l} ϕ^{″} + L e f ϕ^{'} + S r L e θ^{″} = 0 & (13) \end{array}

Where,

\begin{array}{l} λ = \frac{G r_{x}}{R e}, δ = \frac{G c}{R e}, M = \frac{σ {B_{0}}^{2} (x)}{a ρ}, L e = \frac{ν}{D_{B}} P r = \frac{ν}{α}, \\ N_{b} = \frac{τ D_{B} (C_{w} - C_{\infty})}{ν}, N_{t} = \frac{τ D_{t} (T_{w} - T_{\infty})}{ν T_{\infty}}, \\ G r_{x} = \frac{g β_{t} (T_{w} - T_{\infty}) x}{a ν}, R e = \frac{u_{w} x}{ν}, G c_{x} = \frac{g β_{c} (C_{w} - C_{\infty}) x}{a ν}, \\ P r_{N} = \frac{1}{P r} (1 + \frac{4}{3} N), N = \frac{4 σ^{*} T_{\infty}^{3}}{α k^{*}}, \\ D_{f} = \frac{D_{T} K_{T} (C_{w} - C_{\infty})}{ν C_{s} C_{p} (T_{w} - T_{\infty})}, S r = \frac{D_{T} K_{T} (T_{w} - T_{\infty})}{ν T_{\infty} (C_{w} - C_{\infty})}, & (14) \end{array}

Here, primes denote the differentiation with respect to η, λ Buoyancy parameter, δ Solutal buoyancy parameter, M is the magnetic parameter called Hartmann number, ν is the kinematic viscosity of the liquid, Pr denotes the Prandtl number, Le denotes the Lewis number, N_b denotes the Brownian motion parameter, N_t indicates thermophoresis parameter, and N is the radiation parameter.

The corresponding boundary conditions are transformed to:

\begin{array}{l} f (η) = 0, f^{'} (η) = 1, θ (η) = 1, ϕ (η) = 1 a t η = 0, \\ f^{'} (η) \to 0, θ (η) \to 0, ϕ (η) \to 0 a s η \to \infty, & (15) \end{array}

The skin friction, Sherwood number and Nusselt number for the present problem are defined as:

\begin{array}{l} N u_{x} = \frac{x q_{w}}{k (T_{w} - T_{\infty})}, S h_{x} = \frac{x q_{m}}{D_{B} (C_{w} - C_{\infty})}, C_{f} = \frac{t_{w}}{{{u_{w}}^{2} ρ}_{f}} & (16) \end{array}

Where,

\begin{array}{l} q_{w} = - k \frac{\partial T}{\partial y}, q_{m} = - D_{B} \frac{\partial C}{\partial y}, τ_{w} = μ (1 + \frac{1}{β}) \frac{\partial u}{\partial y} a t y = 0 & (17) \end{array}

The associated expressions of dimensionless reduced Nusselt number −θ′(0), reduced Sherwood number −ϕ′(0), and skin friction coefficient C_fx are defined as

\begin{array}{l} - θ^{'} (0) = \frac{N u_{x}}{(1 + \frac{4}{3} N) \sqrt{\frac{m + 1}{2} R e}}, - ϕ^{'} (0) = \frac{S h_{x}}{\sqrt{\frac{m + 1}{2} R e}}, C_{f x} = C_{f} \sqrt{\frac{2}{m + 1} R e} & (18) \end{array}

Where, $R e = \frac{u_{w} x}{ν}$ is the local Reynolds number.

The converted non-linear differential (Equations 9–12) with the boundary conditions (14) are elucidated by the Keller box scheme consisting of the steps; finite-differences technique, Newton's scheme, and the block elimination process clearly explained by Anwar et al. [41]. This method has been extensively applied and it looks to be the most flexible compared to common techniques. It has been presented as much quicker, easier to program, more efficient and easier to practice. Currently, there are many alternative techniques to solve such types of problems [42].

Results and Discussion

This portion of study manages the calculated results of converted non-linear ordinary differential (Equations 8–10) with boundary conditions (12) elucidated via Killer-box method. Concerning numerical results of physical parameters, including Brownian motion parameter Nb, radiation parameter N, thermophoresis parameter Nt, magnetic factor M, buoyancy factor λ, solutal buoyancy factor δ, inclination factor γ, Prandtl number Pr, Lewis number Le, Dufour effect Df, Soret effect Sr, non-linear stretching parameter m, and Casson fluid parameter β, several figures and tables are prepared. In Table 1, in the deficiency of Dufour effect Df, Soret effect Sr, buoyancy parameter λ, solutal buoyancy constraint δ, magnetic factor M, radiation parameter N and non-linear stretching parameter ‘m' K with γ = 90° when Casson parameter β → ∞ produces a reduced Nusselt number −θ′(0), the reduced Sherwood number −ϕ′(0) equate with existing outcomes of Khan and Pop [1]. The consequences establishes a brilliant settlement. The effects of −θ′(0), −ϕ′(0), and C_fx(0), against changed values of involved physical parameters Nb, Nt, M, β, λ, δ, γ, m, Le, Df, Sr, N, and Pr are shown in Table 2. From Table 2 is can be clearly seen that −θ′(0) declines for growing values of Nb,Nt, M,Le, Df, m, γ, β, N, and increases with enhancing numerical values of λ, δ, Sr, and Pr. Moreover, it is perceived that −ϕ′(0) enhanced with the larger values of Nb, λ, δ, Nt, Le, N, Pr, Df, and drops for bigger values of M, m, β, Sr, and γ. Physically, the thermal boundary layer thickness enhances, as the Brownian parameter Nb increases impacting a large extent of the fluid. Moreover, for large values of thermophoresis effects, the Nusselt number decreases and the Sherwood number increases because, the thermal boundary layer becomes thicker due to deeper diffusion penetration into the fluid. On the other hand, C_fx(0) rises with the growing values of Nb, Le, M, β, Pr, γ, m, Df, and drops with the higher values of, λ, δ, Nt, N, and Sr. The current results are novel and show the impact of the buoyancy parameter, solutal buoyancy parameter and inclination parameter impacts on the driven flow in the presence of Soret and Dufour effects on power-law fluid which is currently unavailable in the literature.

TABLE 1

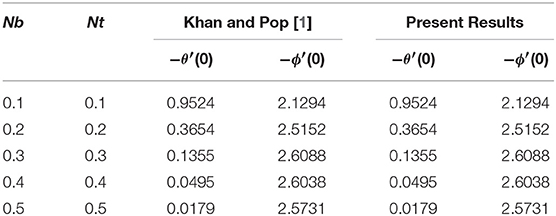
Table 1. Comparison of the reduced Nusselt number −θ′(0) and the reduced Sherwood number −θ′(0) when M, N = 0, β → ∞, δ, Sr, Df, λ = 0, m = 1, Pr = Le = 10 and γ = 90°.

TABLE 2

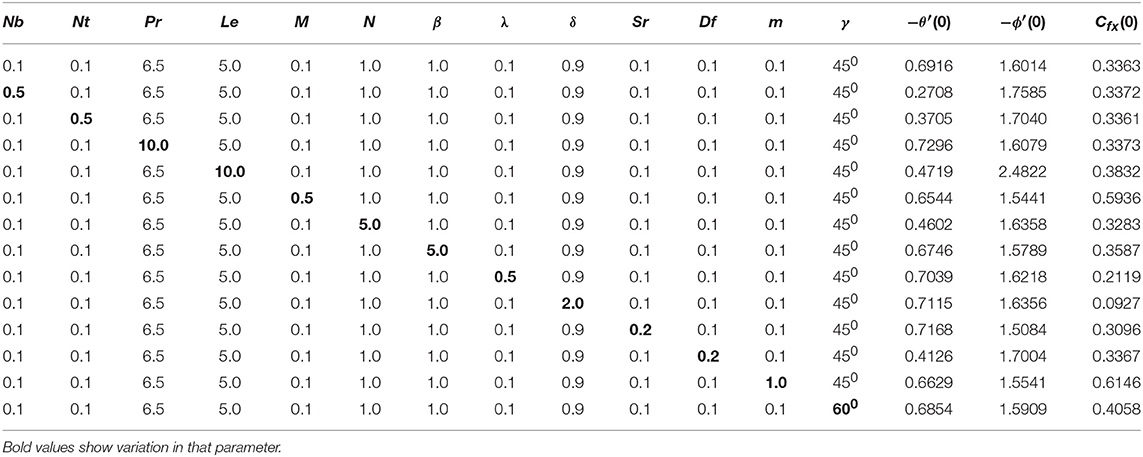
Table 2. Values of the reduced Nusselt number −θ′(0), the Sherwood number −ϕ′(0) and the Skin-friction coefficient C_fx(0).

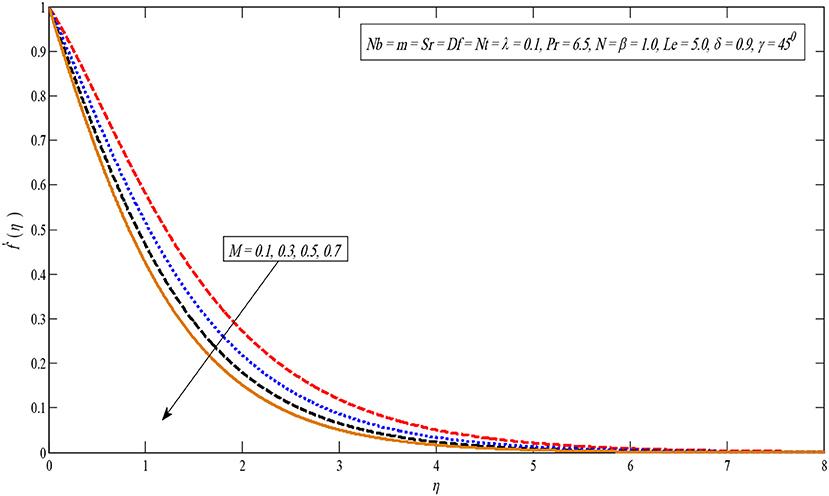
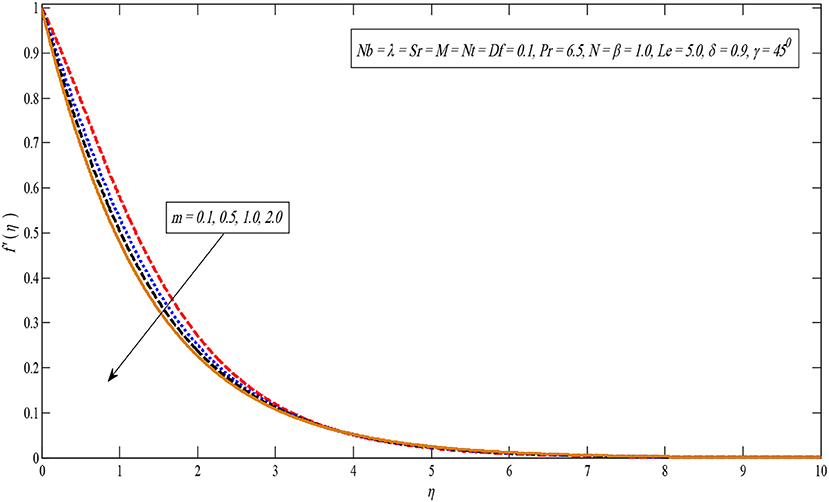
An image of the effect of factor M on velocity profile is portrayed in Figure 2. According to Figure 2, by improving the constraint M, the velocity outline reduces. Since the magnetic field produces Lorentz force, by slowing down the speed of the liquid. On the other hand, the velocity profile slows down for large values of the non-linear stretching parameter m, shown in Figure 3. Physically, the momentum boundary layer thickness reduces for higher values of m.

FIGURE 2

Figure 2. Velocity profile for several values of M.

FIGURE 3

Figure 3. Velocity profile for several values of m.

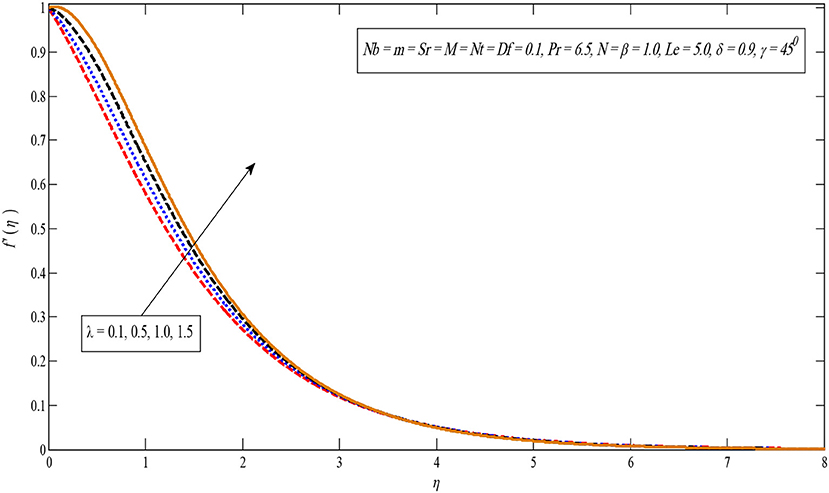
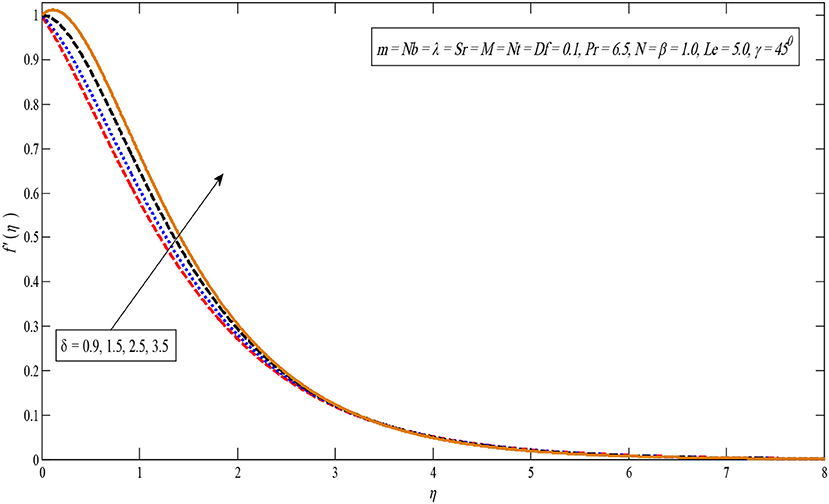
The impact of the buoyancy factor is shown in Figure 4. It is observed that the velocity profile rises by improving the buoyancy limit. It is due to the fact that buoyancy effect increases the strength of the fluid flow whereby the boundary layer thickness and velocity enhances. Figure 5 indicates that the velocity outline increases by enhancing the solutal buoyancy factor. Physically, the buoyancy parameter reduces the viscous forces whereby the velocity upturns. In addition, the opposite impact can be seen in temperature and concentration profiles for large values of δ.

FIGURE 4

Figure 4. Velocity profile for several values of λ.

FIGURE 5

Figure 5. Velocity profile for several values of δ.

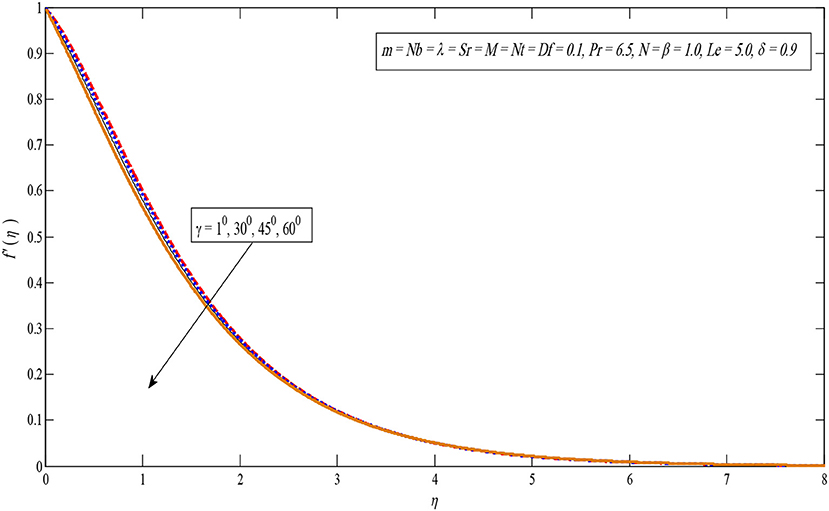
Figure 6 interprets the significance of inclination factor γ on the velocity outline. It is perceived in Figure 6 that the velocity outline runs down by enhancing the values of γ. Moreover, the circumstances indicate that the maximum gravitational force acts on flow in the case of γ = 0, because in this state the sheet will be vertical. On the other hand, for γ = 90⁰, the sheet will be horizontal which causes the decline in velocity profile as the power of the bouncy forces drop.

FIGURE 6

Figure 6. Velocity profile for several values of γ.

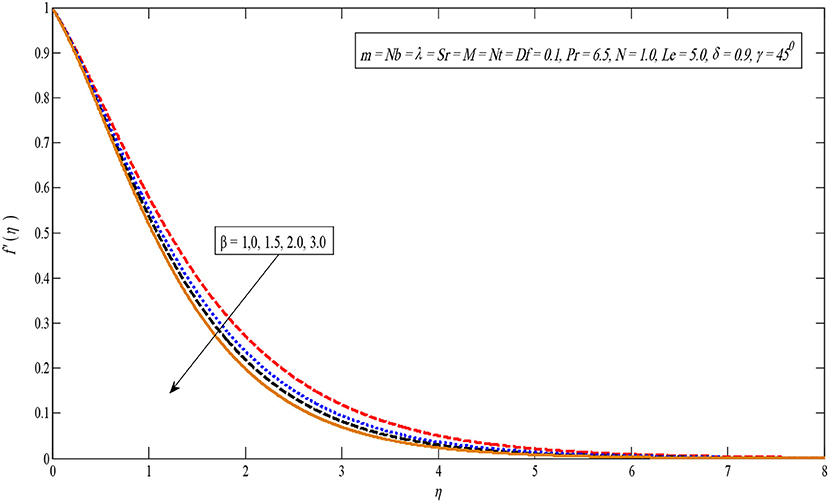
The effect of the Casson parameter on the velocity parameter is presented in Figure 7. It is observed that for large values of the Casson parameter, the velocity profile decreases. The reason behind this behavior is that by increasing the values of the Casson parameter, β increases the fluid viscosity i.e., reducing the yield stress. Therefore, the momentum boundary layer thickness reduces [43].

FIGURE 7

Figure 7. Velocity profile for several values of β.

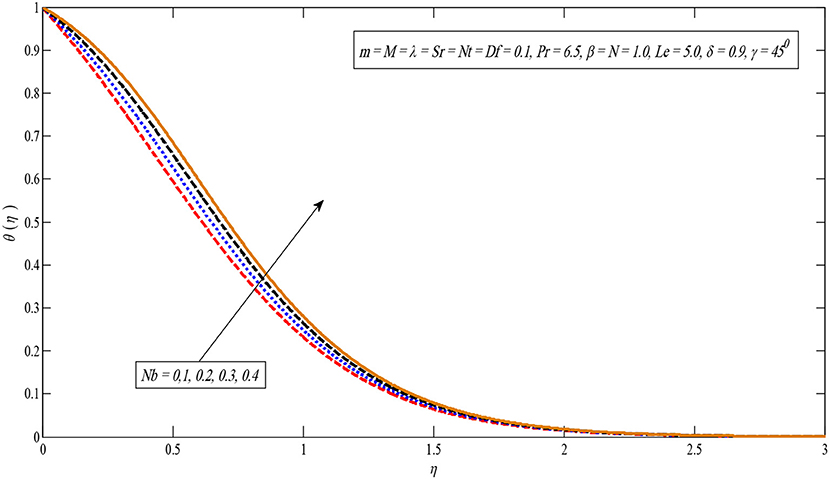
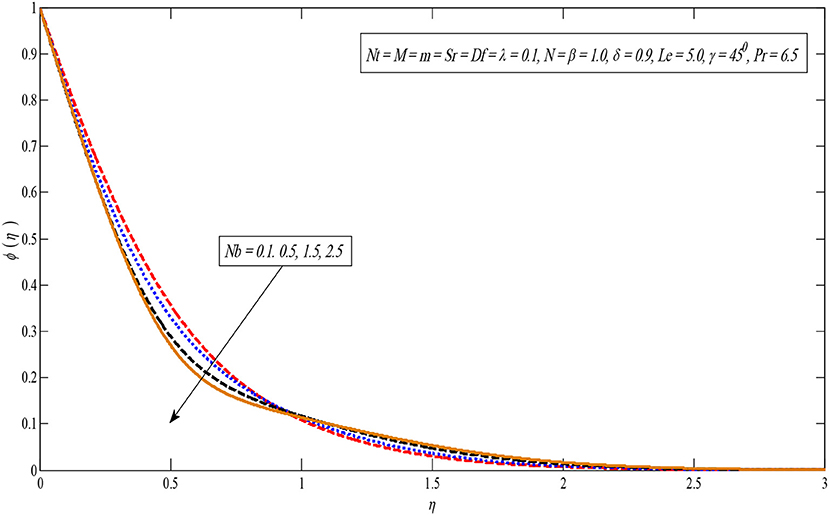
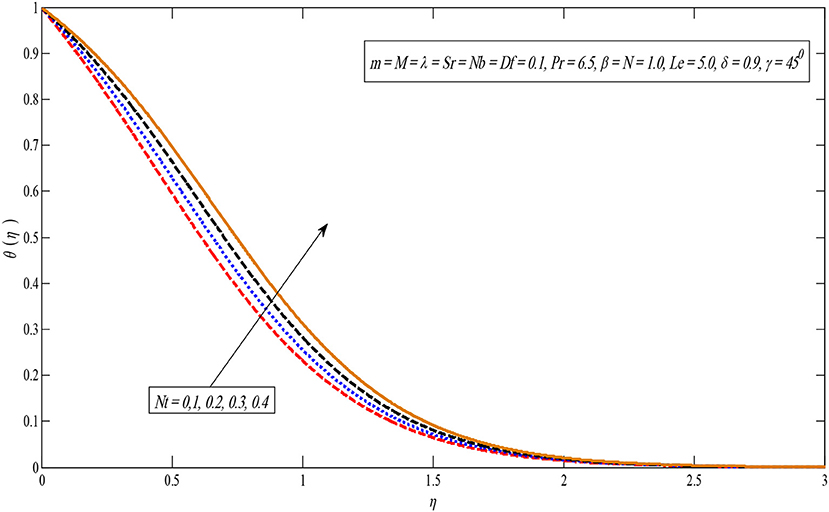
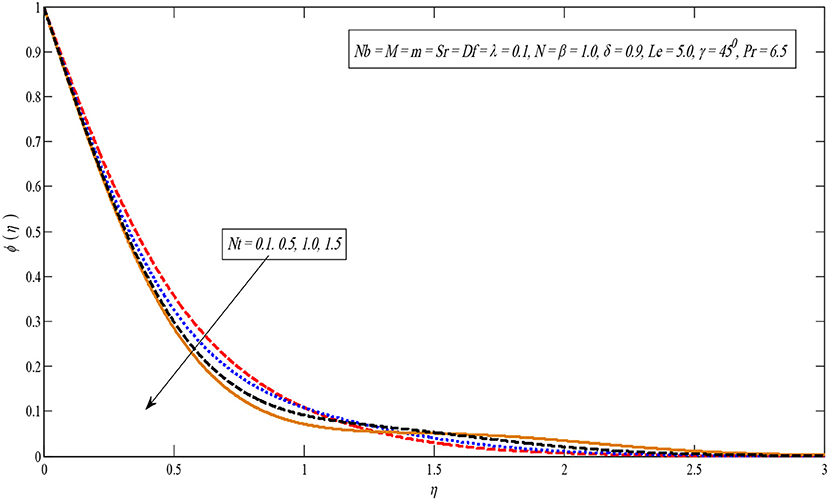
Figures 8, 9 show the effect of the Brownian motion on the temperature and concentration profiles, respectively. The temperature sketch enlarges on enlarging Nb; on the other hand, concentration distribution enlightens a dissimilar style. Physically, the boundary layer heats up due to the development in the Brownian motion which is inclined to transport nanoparticles from the extending sheet to the motionless liquid. Therefore, the absorption nanoparticle lessens. Figures 10, 11 present temperature and concentration profiles for altered values of thermophoresis parameters Nt. It is perceived that both temperature and concentration contours upsurge by growing the thermophoresis parameter because thermophoresis causes the small particles to compel away from a warm surface to the cold one.

FIGURE 8

Figure 8. Temperature profile for several values of Nb.

FIGURE 9

Figure 9. Concentration profile for several values of Nb.

FIGURE 10

Figure 10. Temperature profile for several values of Nt.

FIGURE 11

Figure 11. Concentration profile for several values of Nt.

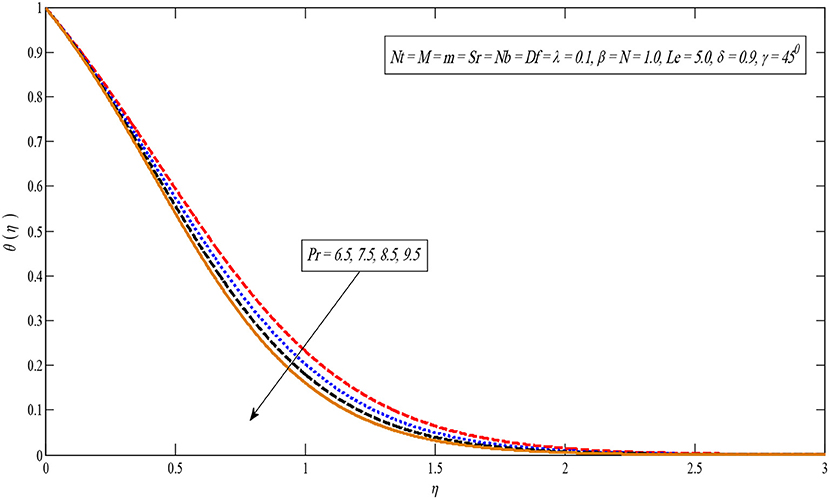
Figure 12 reveals that by growing the values of the Prandtl number parameter Pr, the temperature profile drops because the thermal boundary layer viscosity declines when growing the Prandtl number Pr. In short an upturn in the Prandtl number Pr means a deliberate amount of thermal dispersion.

FIGURE 12

Figure 12. Temperature profile for several values of Pr.

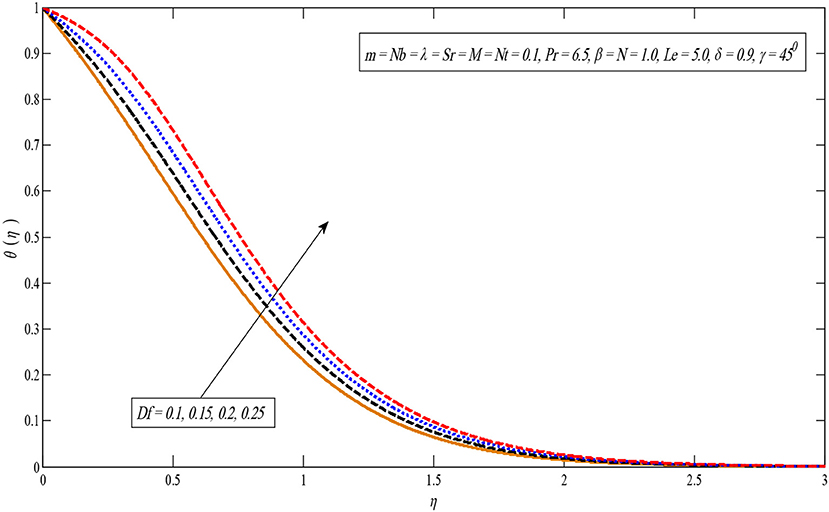
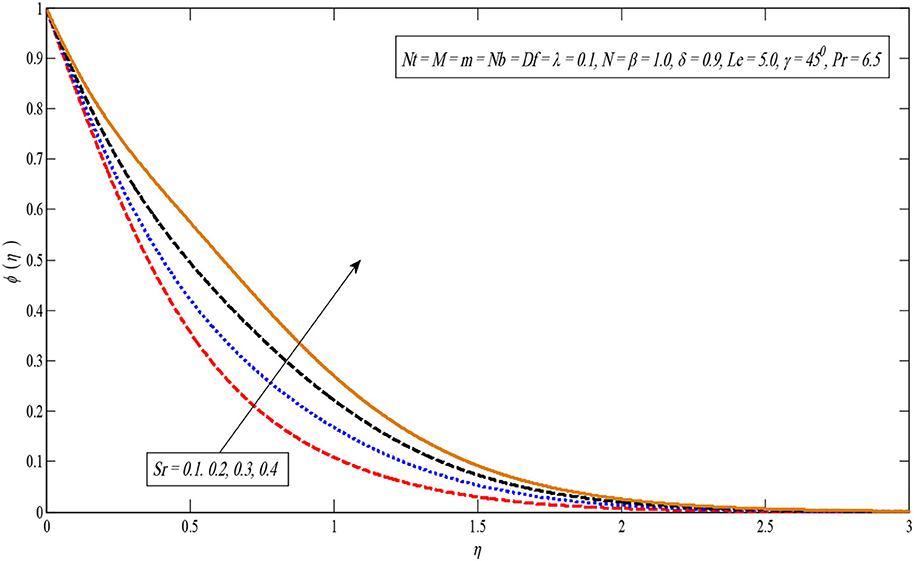
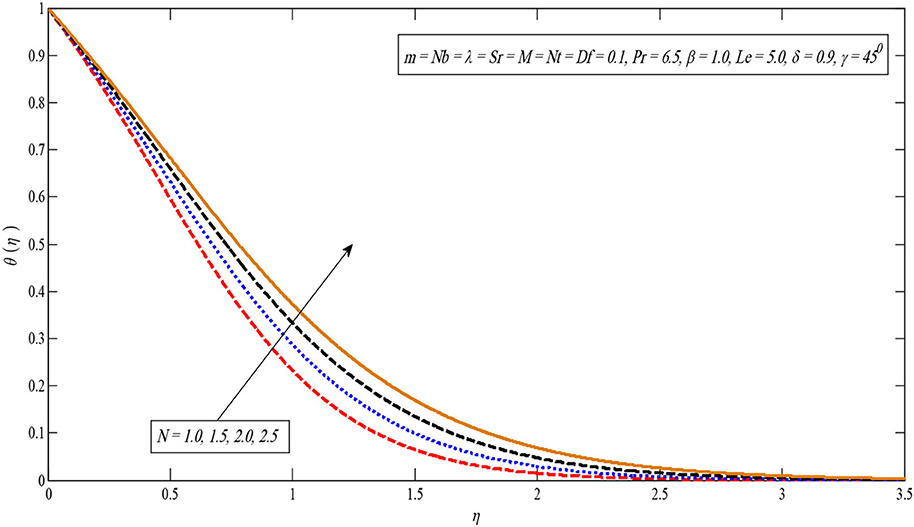
Figure 13 shows that the temperature profile becomes large for larger values in parameter D_f. This can be justified as an increase in the Dufour parameter, causing an increase in the concentration gradient, resulting in a mass diffusion taking place more rapidly. In this way, the rate of energy transfer related to the particles becomes higher. That is why the temperature profiles enhance. The impact of the Soret number on the concentration profile is observed similar to the impact of the Dufour number on the temperature profile. As parameter S_r increases, the concentration profile increases as displayed in Figure 14. Additionally, Figure 15 indicates a temperature profile enhanced for large values of N.

FIGURE 13

Figure 13. Temperature profile for several values of Df.

FIGURE 14

Figure 14. Concentration profile for several values of Sr.

FIGURE 15

Figure 15. Temperature profile for several values of N.

Conclusions

This study explored the heat and mass exchange of Casson nanofluid flow over a non-linear slanted extending sheet. The numerical results are successfully obtained via the Keller-Box method and are finally performed with the resulting outcomes of already published work [1]. The main findings of the current study are summarized as:

• The velocity outline decreases by enhancing the inclination parameter.

• An increment in Casson fluid factor declines the velocity profile.

• Improving the buoyancy and solutal buoyancy parameters cause an enhancement in the velocity profile.

• Temperature profile upturns when increasing the radiation factor.

• Dufour effect causes the enhancement in the temperature profile.

• Mass diffusion and energy of the fluid upturns by enhancing the Brownian motion factor.

• The thermophoresis factor increases the temperature profile and decreases the concentration profile.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The formulation was done by KR and MA. Similarity transformation was done by MM. Problem solved by IK and SA. Results plotted and discussed by PT and KN. All authors equally contributed in writing this manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author (SA) would like to thank the Deanship of Scientific Research (DSR) Majmaah University for supporting this work.

References

1. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Trans. (2010) 53:2477–83. doi: 10.1016/j.ijheatmasstransfer.2010.01.032

ORIGINAL RESEARCH article

Numerical Solution of Casson Nanofluid Flow Over a Non-linear Inclined Surface With Soret and Dufour Effects by Keller-Box Method

Introduction

Problem Formulation

Results and Discussion

Conclusions

Data Availability Statement

Author Contributions

Conflict of Interest

Acknowledgments

References

This article is part of the Research Topic

People also looked at